单管计算电容式液位传感器的仿真与特性研究
2017-06-22李东升
王 颖,禹 静,李东升,于 航
(中国计量大学计量测试工程学院,杭州 310018)
单管计算电容式液位传感器的仿真与特性研究
王 颖,禹 静,李东升*,于 航
(中国计量大学计量测试工程学院,杭州 310018)
计算电容式液位传感器采用计算电容原理,经过单管式轻量化的结构改良设计。为探究改良结构对传感器特性的影响,针对单管计算电容式液位传感器建立有限元模型,利用分析软件ANSYS仿真分析几个重要结构参数对传感器灵敏度的影响。特性试验表明:传感器输入输出曲线与仿真结果具有良好的一致性;在0~200 mm量程内传感器线性度为±0.8%,回程误差为±0.03 pF,液位测量的最大引用误差为-1.0% FS。该研究为计算电容式液位传感器的结构优化提供了理论基础,有利于该新型传感器在航空、航天燃料液位测量领域的应用推广。
单管液位传感器;计算电容原理;传感器仿真;燃料液位测量
液位测量技术在工程领域中起着重要的作用,根据测量原理的不同,液位测量方法有微波式、电容式、超声波式、差压式和电导式等。其中电容式液位传感器以其灵敏度高、分辨力强、能在恶劣环境下工作等优点被用于各种测量场合[1-2]。但是传统的电容式液位传感器采用双层套筒结构不够轻量化,并且当内外电极间隙较小时,容易引起毛细现象,出现迟滞,降低响应速度,同时存在内外电极同轴度装配及加工误差[3],限制了其在航空、航天燃料液位等高要求测量场合的应用。
计算电容在计量领域内用于复现电磁单位,标准不确定可达10-8量级。其单位长度上的电容与直径无关,总电容量一般与轴向长度有关。计算电容以其误差源少、稳定性高等优势,被用于研制新型传感器[4-5]。Mathfoozur Rehman 等人采用Thompson结构[6],研制出了高灵敏度(0.14 Pa)、高线性度(0.1%)的测微压力计[7]。韩国Rae Duk Lee等人采用计算电容结构测量液体介电常数,标准不确定度为±0.02%[8]。目前,较少文献涉及计算电容在测量液位方面的应用研究。
于航等人[3]提出的计算电容式液位传感器基于计算电容原理,采用单管式电容结构实现轻量化设计,但这一结构上的改良对传感器特性以及液位测量带来的影响尚知甚少,传感器结构也有待优化。本文旨在应用有限元分析软件ANSYS的静电场模块,利用参数化设计语言APDL编写程序,实现对单管计算电容式液位传感器的仿真与分析,从而为后续传感器结构参数的优化设计奠定基础。
1 单管计算电容式液位传感器的结构与测量原理
计算电容式液位传感器利用计算电容原理[6]中交叉电容器在单位长度上的总电容具有高稳定性的特点设计,其机械结构如图1所示。
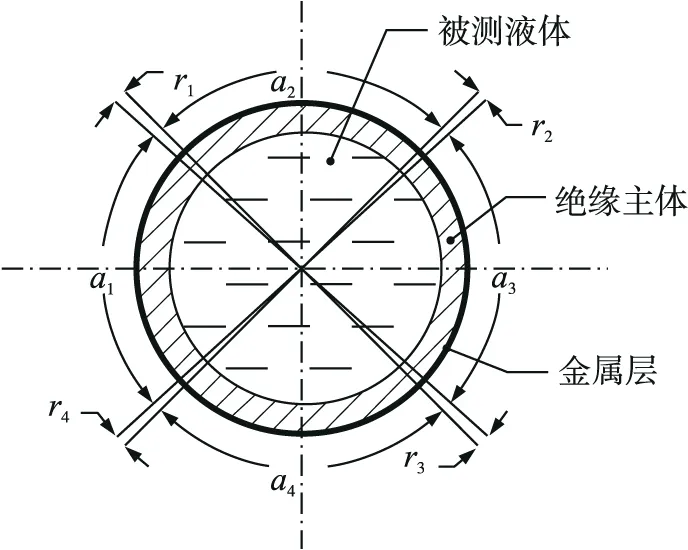
图1 计算电容式液位传感器
区别于传统电容式液位传感器的双层套筒机构,采用单管式轻量化设计,仅由绝缘主体与金属层两部分简单构成。绝缘主体采用石英管材质,呈空心圆柱形,中空区域用以盛装被测液体。石英管外壁镀有金属层——铜膜,铜膜圆周上呈90°间隔分别刻蚀四条微小间隙,每条微小间隙对应圆心角rm相等,且rm≪90°(m=1,2,3,4)。两两微小间隙之间所夹的4个铜膜区域形成4个极板,每个极板对应圆心角an≈ 90°(n=1,2,3,4)。每相对的两个极板分别为激励极板和检测极板,形成一个电容输出,从而构成计算电容原理中的交叉电容器。
假设计算电容式液位传感器的轴向长度为l,被测液位lx为:
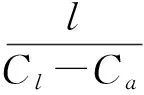
(1)
式中:Ca、Cl、Cx分别为传感器在空管、满管及在当前被测液位时的输出电容。
由式(1)可知,被测液位与传感器输出电容值呈线性关系。单管计算电容式液位传感器的测量精度理论上只取决于交叉电容器轴向长度和输出电容值的测量,几乎能够消除加工及装配引起的误差。其中,传感器输出电容值受多个结构参数及边缘效应的影响,本文利用有限元法对传感器结构进行仿真分析。
2 传感器有限元模化与仿真分析
2.1 有限元模型的建立
单管计算电容式液位传感器采用低频激励,频率小于1 MHz,轴向长度为200 mm,石英管外径为25 mm,两者之比大于1.5倍,可视为静电场问题[9-10]。将三维的计算电容式液位传感器简化为二维静电场,作如下几点假设:①测量过程中,管道内流体、流型不变;②极板轴向边缘效应可忽略;③石英管外电荷被完全屏蔽,无空间自由电荷。
传感器的数学模型可用二维静电场的泊松方程表示[11]:
[ε0ε(x,y)·φ(x,y)]=0
(2)
式中:ε0为真空介电常数,ε(x,y)为传感器内介质的相对介电常数分布函数,φ(x,y)为传感器内的电势分布函数。
设对应圆心角an(n=1,2)的极板为两个激励极板i(i=1,2),对应圆心角an(n=3,4)的极板为两个检测极板j(j=1,2)。
采用第1类边界条件(狄利克雷条件)[12],对传感器的一个激励极板i(i=1/i=2)施加激励电压U,另一个激励极板i(i=2/i=1)以及两个检测极板j(j=1,2)上施加电压为0,表达式为:
(3)
式中:Xi(i=1,2),Xj(j=1,2)分别为传感器的两个激励极板、两个检测极板上的节点所组成的集合。
每一对激励与检测极板之间的感应电荷Qij(i=j)可由下式计算得到[13]:
(4)
式中:ε0为真空的介电常数,ε为被测液体的相对介电常数,Γj为沿检测极板边缘逆时针方向定义的积分路径,n为曲线Γj的单位法向量,E为电场在积分路径上的映射。
因此,在轴向单位长度上,每一对激励与检测极板之间的电容Cij(i=j)为:
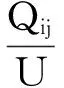
(5)
式中:U为激励极板上施加的激励电压。
分别求得激励极板i(i=1/i=2)被施加电压U时,当前激励极板与其对应检测极板之间的电容输出C11、C22,则传感器在单位长度上的仿真输出电容为:
C=(C11+C22)/2
(6)
二维静电场仿真中,传感器在单位长度上的仿真输出电容即为传感器的灵敏度(单位液位变化引起传感器的输出电容变化),本文以灵敏度为传感器结构参数仿真分析指标,灵敏度值越大,传感器对液位变化越灵敏。
2.2 ANSYS仿真实现
ANSYS软件的有限元分析步骤包括:创建几何模型、定义材料属性、划分网格、施加载荷、求解及结果显示等[12]。
采用ANSYS14.0中的参数化语言APDL编写针对单管计算电容式液位传感器的仿真程序。定义二维实体单元PLANE121,传感器结构参数为:石英管内半径R0=10.5 mm,石英管外半径R1=12.5 mm,铜膜厚度d=0.5 mm,极板间隙张角θ=2.3°,极板长度H=200 mm。根据传感器结构参数建立几何模型,并定义材料属性:石英管介电常数为3.7 F/m,石英管内被测液体为无水乙醇,其介电常数为25.7 F/m。
采用自由三角形网格剖分,考虑到越靠近极板电场分布越强,对越靠近极板的区域进行更为细密的网格划分。结合各面域的几何尺寸,网格边长设置如下:被测液体区域网格边长为1.5 mm,石英管区域网格边长为0.9 mm,极板区域网格边长为0.1 mm。网格划分后,传感器区域内共生成单元数为8 388,节点数为17 617。
根据狄利克雷边界条件给传感器的各极板施加载荷并求解。如图2、图3所示为对激励极板i(i=1)施加载荷U=1 V,对激励极板i(i=2)以及两个检测极板j(j=1,2)上施加电压为0的边界条件下求解得到的传感器电势等值云图及电场强度矢量图。

图2 电势等值云图
从图2可以看到,仅激励极板i(i=1)上的电势为最大值1 V,其余极板上电势均为最小值0 V,传感器中间区域的电势由激励极板i(i=1)向检测极板j(j=1)方向,呈波面形由最大值向最小值过渡。图3中,激励极板i(i=1)两侧间隙区域的电场强度最大可达1.21 V/m左右,且电场方向由间隙向外呈辐射状,该区域存在边缘效应。激励极板区域电场强度均匀分布在0.13 V/m~0.26 V/m左右,电场方向由极板指向传感器几何圆心;传感器其他区域的电场强度基本较弱,方向由传感器几何圆心径向向外。
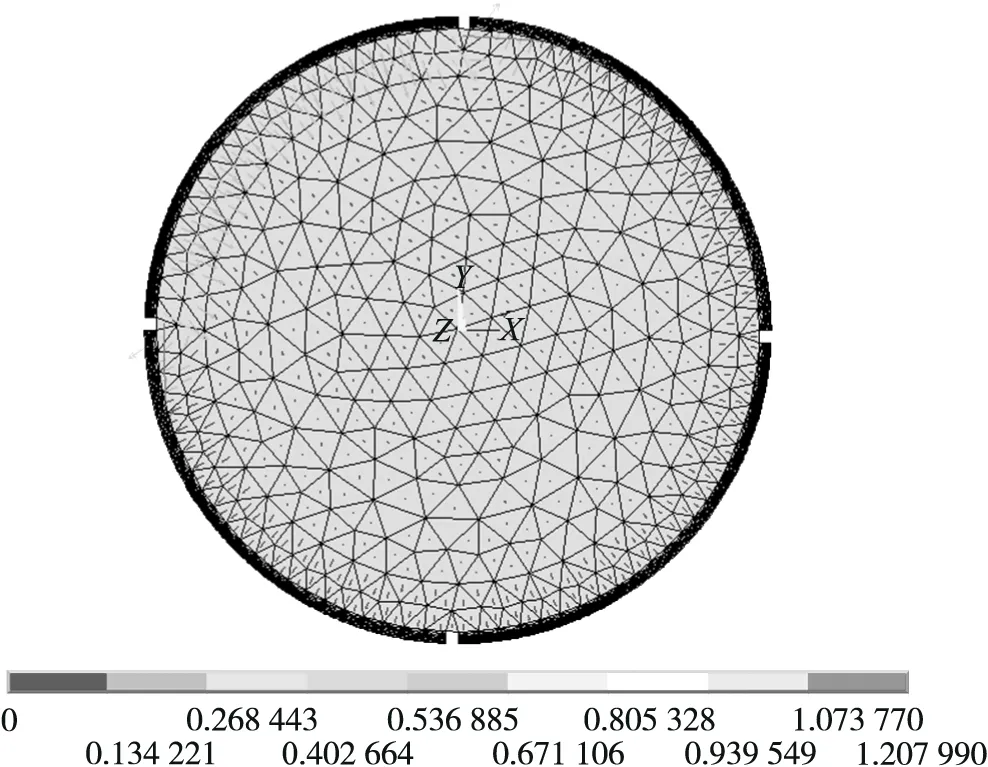
图3 电场强度矢量图
分别对两个激励极板i(i=1/i=2)施加载荷,沿对应检测极板边缘逆时针定义积分曲线,将电场矢量和积分曲线的单位法向量映射到积分路径上,由式(4)、式(5)计算得到C11=0.066 5 pF/mm,C22=0.066 4 pF/mm。因此,传感器灵敏度即轴向单位长度上的仿真输出电容C=0.066 45 pF/mm,进而可以计算得到传感器在量程0~200 mm范围内的电容输出情况。
同理,对传统双层套筒式液位传感器进行仿真得到其灵敏度为0.051 95 pF/mm,相比单管计算电容式液位传感器的灵敏度较低,同时存在内外圆筒式电极同轴装配误差以及毛细现象引起响应迟滞等结构缺陷。理论上,计算电容式液位传感器较传统液位传感器具备测量灵敏度高、结构轻量化等优势。
2.3 结构参数对传感器灵敏度的影响
以灵敏度为评价指标,采用单一变量原则,分析结构参数对传感器特性的影响。
①屏蔽层
首先分析有无屏蔽层对传感器输出电容的影响。在传感器外侧添加一个同轴装配的内径为30 mm的屏蔽层,仿真得到传感器的灵敏度为0.071 3 pF/mm,与没有屏蔽层的情况相比,灵敏度提高了7.2%。可见,利用屏蔽层减弱外界电磁干扰,可以有效提高传感器输出电容对液位变化的灵敏度。
②极板间隙张角
传感器的交叉电容结构中,极板间隙张角与传感器灵敏度的关系曲线如图4所示。传感器灵敏度在极板间隙张角θ=2.6°时取到最大值。θ=2.6°以左,随着极板间隙张角的减小,灵敏度逐渐减小,这是由于边缘效应影响了极板附近电场的分布;θ=2.6°以右,随着极板间隙张角的增大,灵敏度逐渐减小,这是由于极板的有效长度减小,电荷分布减少。因此,在传感器极板间隙张角的设计时,要综合考虑边缘效应与极板有效长度的影响。

图4 极板间隙张角与传感器灵敏度的关系曲线
③石英管内半径
计算电容式液位传感器的灵敏度随石英管内半径的变化曲线如图5所示。石英管内半径越大,传感器单位长度上的电容输出也越大。但在传感器结构设计时,同时也要考虑传感器的体积与加工成本等因素,应权衡利弊。

图5 石英管内半径与传感器灵敏度的关系曲线
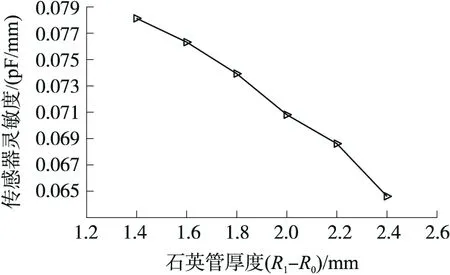
图6 石英管厚度与传感器灵敏度的关系曲线
④石英管厚度
从图6可以看出,传感器灵敏度随着石英管厚度的增加而减小。理论上,在传感器结构参数选择时,石英管越薄越好;实际设计时,还应综合考虑太薄的管壁是否能够承受被测液体的液压以及传感器结构是否牢固等因素。
⑤屏蔽层与极板间距
本文还分析了屏蔽层与极板间距对传感器单位长度电容输出的影响。图7中,随着屏蔽层与极板间距由1.5 mm逐渐增加到4 mm,传感器灵敏度仅在0.000 25 pF/mm的小幅度内变化,可见屏蔽层与极板间距对屏蔽外界电磁干扰等效果的影响很细微,可忽略不计。传感器设计时,可从成本经济、装配方便等角度合理选择屏蔽层内径大小。

图7 传感器灵敏度随屏蔽层与极板间距的关系曲线

图8 实验装置实物图
3 传感器特性研究
本文自行设计实验平台进行传感器的特性测试。实验装置实物图如图8,单管计算电容式液位传感器由支架和夹具固定在容量为250 mL量筒内,量筒外壁附有最小分度值为0.5 mm的菲林尺,用于确定实验时被测液体的当前液位高度。采用同惠TH2617型电容测量仪测量传感器输出电容值,该电容测量仪的最小分辨力为0.000 1 pF,测量精度为0.05%。以纯度为99.8%的无水乙醇作为被测液体,在测试电平1 V、测试频率100 kHz、测量数据10次平均显示的实验条件下,分别对电容C11、C22进行测量,从而取两者平均作为传感器输出电容值C。每次测试前,对液位0 mm处进行校准清零,消除杂散电容、电磁噪声等对电容测量的影响。测量过程中,用容量为10 mL的滴管每次增高20 mm液位,待液面稳定后点击“开始”并记录一个电容读数。
3.1 实验数据与仿真结果对比
将传感器输出电容的实验值与仿真值进行对比,如图9所示。可以看到,仿真与实验两种情况下,单管计算电容式液位传感器的输出输入特性曲线变化趋势基本一致,两者误差控制在1.8% FS内。在量程前半程,仿真输出电容值与实验值较为接近;后半程,两者误差较前半程偏大。经分析认为,可能是传感器极板轴向中点处设计有信号线引出连接点造成。此外,实验过程中,被测液体介电常数、测试电平以及测试频率的浮动、极板之间的边缘效应等都会对输出电容值的测量带来影响,从而造成了仿真与实验值之间的偏差。

图9 传感器仿真与实验特性曲线对比
3.2 传感器特性分析
单管计算电容式液位传感器在去程-回程时的输出输入特性曲线如图10所示。当液位在0~200 mm范围内以20 mm间隔变化时,输出电容值C在0~14 pF范围内呈线性变化。采用最小二乘法拟合线性化,获得传感器的线性度为±0.8%。比较传感器正反行程输出输入数据可得回程误差为±0.03 pF。
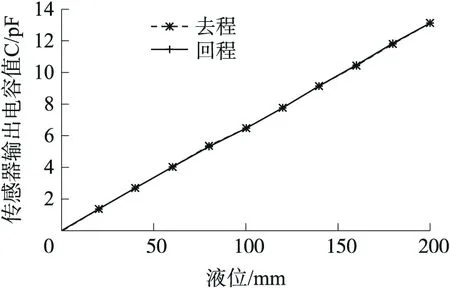
图10 传感器输出输入特性曲线
将实验测得传感器空管、满管及各液位处的输出电容值代入式(1),并结合极板长度H=200 mm即可求得传感器在量程内的液位实测值,见表1。传感器液位测量误差曲线如图11所示。可以看到,单管计算电容式液位传感器在液位为120 mm处取到最大引用误差为-1.0% FS。测量误差近似关于量程中点呈原点对称,在前半程误差为正,后半程误差为负;在量程两端及中点附近,液位测量误差较小,接近于0,符合传感器测量误差越靠近量程中点越小的一般情况。该实验结果表明,经过单管式结构改良的传感器能兼顾实现轻量化与液位测量。可通过增加屏蔽措施,改善机械工艺,进一步提高传感器的测量精度,从而有利于该新型传感器在航空、航天燃料液位测量上的应用推广。
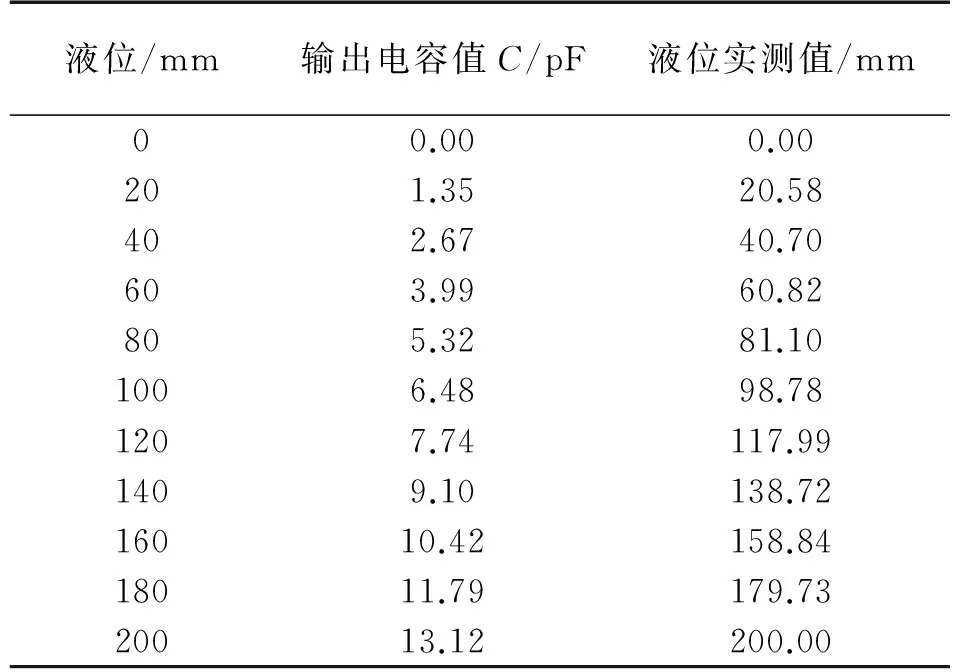
表1 传感器输出电容值与液位实测值

图11 传感器液位测量误差曲线
4 结论
①针对单管计算电容式液位传感器的测量原理,推导出了有限元仿真模型,运用分析软件ANSYS,仿真分析了有无屏蔽层、极板间隙张角、石英管内半径、石英管厚度及屏蔽层与极板间距对传感器灵敏度的影响。
②通过对比实验与仿真情况下传感器的输出输入特性曲线,验证了单管计算电容式液位传感器仿真过程的合理性,为传感器结构工艺的优化设计,提高传感器性能提供了研究依据。
③特性实验表明,经过单管式轻量化结构改良后的液位传感器在量程内具有良好的线性度,也探究了应用计算电容原理提高液位传感器回程误差和测量误差的可能性。
[1] 田海军,张鋆,李帅男等. 五段式电容液位测量变送器的研究[J]. 机床与液压,2015,43(20):136-139.
[2] 徐驰,孙长库,王鹏,等. 液位实时自动跟踪测量系统[J]. 传感技术学报,2011,24(10):1506-1510.
[3] 于航,禹静,李东升,等. 单管计算电容式燃料液位传感器理论特性研究[J]. 传感技术学报,2016,29(5):681-685.
[4] 黄璐,陆祖良,杨雁,等. 殷钢电补偿电极补偿立式计算电容端部效应的研究[J]. 电测与仪表,2014,51(5):5-10.
[5] 陆祖良,黄璐,杨雁,等. 可动屏蔽型计算电容复现电容单位的方法研究[J]. 计量学报,2014,35(6):521-527.
[6] Thompson A M,Lampard D G. A New Theorem in Electrostatics and Its Application to Calculable Standards of Capacitance[J]. Nature,1956,177:888.
[7] Rehman M,Murti V G K. A Sensitive and Linear Pressure Transducer[J]. Journal of Physics E:Scientific Instruments,1981,14(8):988-991.
[8] Lee R D,Kim H J,Semenov Y P. Precise Measurement of the Dielectric Constants of Liquids Using the Principle of Cross Capacitance[J]. IEEE Transactions on Instrumentation and Measurement,2001,50(2):298-301.
[9] 张立峰,王化祥. 多相流电容层析成像系统的仿真研究[J]. 电力科学与工程,2005,20(1):8-10.
[10] 陈阳,陈德运,郑贵宾,等. 电容层析成像系统径向电极对传感器性能及敏感场分布的影响[J]. 中国电机工程学报,2005,25(21):152-158.
[11] Shafquet A,Ismail I,Jaafar A. Modeling and Simulation of Multi-Plane Electrical Capacitance Tomography Sensor for Flow Imaging by Using Finite Element Analysis[C]//2014 5th International Conference on Intelligent and Advanced Systems(ICIAS). IEEE,2014:1-6.
[12] 沙星宇. 电容传感器三维有限元模型研究及优化设计[D]. 东北大学,2012.
[13] 周云龙,衣得武,高云鹏. 基于ANSYS的ECT系统传感器的仿真研究[J]. 化工自动化及仪表,2011,38(3):339-341.
Research on the Simulation and Characteristic of Single-Tube Cross Capacitance Liquid Level Sensor
WANG Ying,YU Jing,LI Dongsheng*,YU Hang
(College of Metrology and Measurement Engineering,China Jiliang University,Hangzhou 310018,China)
Cross capacitance liquid level sensor is based on the principle cross capacitance. This is designed to form a single tube,which made it lightweight. In order to study the effects of the new structure on the transducer characteristic,the finite element model was deduced,then realized simulation analysis of the influence of several important structure parameters on the sensor sensitivity in use of the finite element software ANSYS. The results of characteristic test indicate that,the real input-output curve has a good consistency with the simulation results;during the range of measurement 0~200 mm,the sensor linearity is ±0.8%,the return stroke error is ±0.03 pF and the maximum quoted error of level measurement is -1.0% FS. The research provides scientific basis for optimizing the new sensor and is conductive to its application to fuel level measurement in aviation and aerospace.
single-tube liquid level sensor;principle cross capacitance;transducer simulation;fuel level measurement

王 颖(1990-),女,汉族,浙江绍兴人,硕士研究生,研究方向为新型传感技术,oliviacrystal@qq.com;

禹 静(1986-),女,青海西宁人,博士,研究方向为气体静压导轨微振动技术;

李东升(1957-),男,汉族,吉林梨树人,教授,博士,博士生导师,研究方向为超精密工程技术、新型传感技术等,lidongsheng@cjlu.edu.cn。
项目来源:国防科工局技术基础“十二五”科研项目,科工技[20××]8××号。
2016-08-26 修改日期:2017-02-15
TP212.1
A
1004-1699(2017)06-0893-06
C:7110;7230
10.3969/j.issn.1004-1699.2017.06.015
