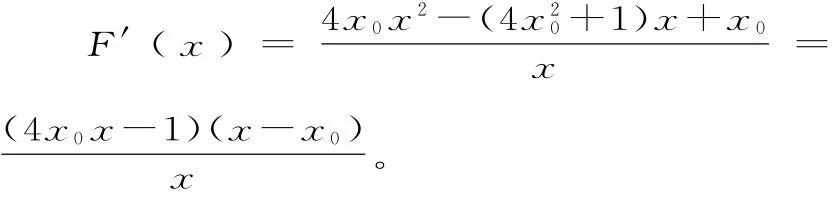扫描导数应用新动向

■安徽省阜阳市太和中学 岳 峻

扫描导数应用新动向

■安徽省阜阳市太和中学 岳 峻

一、活用求导法则

含有导函数的不等式的求解问题是许多同学的弱项,突破此类问题的主要思路是:首先,熟练运用基本函数的求导法则与导数的四则运算法则,做到“正用、逆用、变形用”,透彻理解导数的本质:借助于导数与零的大小关系判断函数的单调性;其次,认真观察含有导函数的代数式的结构,注重分析待解不等式的结构特点,找出条件与结论之间的内在联系;最后,根据已知信息的特点,联想基本函数的求导法则与导数的四则运算法则,构造相应的函数,利用构造的函数的单调性达到求解问题的目的。

(2016年山西一模)设函数f(x)在R上存在导函数f'(x),对于任意的实数x,有f(x)+f(-x)=2x2,当x∈(-∞,0]时,f'(x)+1<2x。若f(2+m)-f(-m)≤2m+2,则实数m的取值范围是____。

解析:构造函数g(x)=f(x)-x2+x,则g'(x)=f'(x)-2x+1。由f'(x)+1< 2x,知g'(x)=f'(x)-2x+1<0,所以g(x)在(-∞,0]上单调递减。因为f(x)+ f(-x)=2x2,所以g(-x)+g(x)=0,所以g(x)是奇函数,所以g(x)在R上单调递减。而f(2+m)-f(-m)≤2m+2,则g(2+m)≤g(-m),所以2+m≥-m,即m≥-1。故实数m的取值范围是[-1, +∞)。

点评:条件中的关键信息是f'(x)+1< 2x,其结构是f'(x)+kxn+t的形式,这是哪个函数的导数呢?因此,构造函数h(x)=,则h'(x)=f'(x)-kxn。

二、函数的拆分

(河南省豫北名校联盟2017届高三上学期精英对抗赛)已知函数f(x)=,曲线f(x)在点(e,f(e))处的切线与直线e2x-y+e=0垂直(e为自然对数的底数)。

(1)若函数f(x)在区间(m,m+1)上存在极值,求实数m的取值范围;

所以g(x)在区间(1,+∞)上是增函数,所以g(x)>g(1)=2,故

所以当x>1时,h'(x)<0,故函数f(x)在区间(1,+∞)上是减函数,所以h(x)<。所以,即

点评:本题主要是第(2)小题的待证不等式比较复杂,解决的关键是将其转化为易于研究的两个函数分别加以研究,灵活地进行放缩达到证明的目的,2016年山东卷理第21题的解答就是采用这种方法。本题的证明转化为

三、存在性问题

(1)求f(x)的解析式及单调递减区间;

(2)若存在x0∈[e,+∞),使函数成立,求实数a的取值范围。

由f'(x)<0,解得0

若a≤e,则g'(x)≥0在x∈[e,+∞)上恒成立,所以g(x)在[e,+∞)上单调递增,,所以。又a≤e,所以

若a>e,则g(x)在[e,a)上单调递减,在(a,+∞)上单调递增,所以g(x)在[e, +∞)上的最小值是g(a)。又因为g(a)<,而a>e,此时一定满足条件。

点评:本题主要考查的是含参不等式的存在性,正确地变换分离参数是解决此类问题的关键。通过分离参数可转化为存在a> h(x)或ah(x)max或a< h(x)min即可,利用导数知识结合单调性求出h(x)min或h(x)max即可得解。

四、恒成立问题

(1)当a=1时,求函数f(x)在点(3, f(3))处的切线方程;

(2)求f(x)的单调区间;

(3)若f(x)在x0处取得极值,且x0∉[e+2,e3+2],而f(x)≥0在[e+2,e3+2]上恒成立,求实数a的取值范围(其中e为自然对数的底数)。

因为x>2,所以x-2>0。

①当a<0时,(x-1)2-(a+1)= x(x-2)-a>0在x∈(2,+∞)上成立,所以f'(x)在x∈(2,+∞)上恒大于0,故f(x)在(2,+∞)上是增函数。

综上:当a<0时,f(x)在(2,+∞)上为增函数;当a>0时,f(x)在)上为增函数,在()上为减函数。

(3)由(2)知f(x)在x0处有极值,故a>0,且

因为x0∉[e+2,e3+2],且e+2>2,所以f(x)在[e+2,e3+2]上单调。

①当[e+2,e3+2]为增区间时,f(x)≥0恒成立,则有2e3。

②当[e+2,e3+2]为减区间时,f(x)≥0恒成立,则有,解集为空集。

综上:实数a的取值范围是(e6+2e3, +∞)。

点评:本题主要考查的是含参不等式的恒成立问题,正确分离参数是关键,也是常用的一种手段。通过分离参数可转化为a> h(x)或ah(x)max或a

五、新定义概念问题

(1)求实数a的值。

(2)定义:定义域为M的函数y=h(x)在点P(x0,h(x0))处的切线方程为l:y= g(x),若在M内恒成立,则称P为函数y=h(x)的“类对称点”。问:函数y=f(x)是否存在“类对称点”。若存在,请至少求出一个“类对称点”的横坐标;若不存在,请说明理由。

当a=1时,f'(x)≥0,函数f(x)单调递增,无极值。

当00,f(x)单调递增;在区间上,f'(x)<0,函数f(x)单调递减;在区间上,f'(x)>0,f(x)单调递增。所以,当x=1时,函数f(x)有极大值,不满足条件。

故所求实数a的值为4。

(2)由(1)可得f(x)=2x2-5x+lnx,所以

函数f(x)在点P(x0,f(x0))处的切线方程为,函数y=f(x)是否存在“类对称点”等价于:当0x0时, f(x)-g(x)>0恒成立。

令F(x)=x0[f(x)-g(x)]=2x0x2-,则x0-x0lnx0=0。

当0

0x)上恒成立,所以,得

0

当x>x0时,要F(x)=f(x)-g(x)> 0恒成立,只需F(x)在(x0,+∞)上是增函数,只要4xx-1>0,即在(x,

00+∞)上恒成立,所以,得

点评:本题借助于“类对称点”的新定义概念,考查函数与导数的应用。求解此类问题需紧扣新定义概念的理解,灵活地运用相关的知识点来分析。

(责任编辑 王福华)