归纳函数与导数的综合应用

2017-06-22湖北省巴东县第三高级中学刘德龙

中学生数理化(高中版.高考数学) 2017年5期

■湖北省巴东县第三高级中学刘德龙

归纳函数与导数的综合应用

■湖北省巴东县第三高级中学刘德龙

一、指数问题

研究表明,当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就检测不到碳14了。碳14的“半衰期”为5730年,若某一死亡生物组织内的碳14经过n(n∈N*)年后用一般的放射性探测器就检测不到碳14了,则n的最小值为( )。

A.1000 B.5730 C.11460 D.57300

解析:设经过m个“半衰期”,某一死亡生物组织内的碳14经过n(n∈N*)年后用一般的放射性探测器就检测不到碳14了。依题意,,即2m>1000(m∈N*)。因为210=1024,所以m的最小值为10。所以n=5730m=57300(年)。故选C。

点评:本题是人教A版必修1第二章第59页习题A组第9题,第67页例6,通过生物机体内碳14的“半衰期”考查指数的计算与指数函数的性质。

变式1:研究表明,当死亡生物组织内的碳14的含量不足死亡前的千分之一时,用一般的放射性探测器就检测不到碳14了。碳14的“半衰期”为5730年,死亡生物组织内的碳14经过12个“半衰期”后的含量约为死亡前的( )。

解析:由已知得,死亡生物组织内的碳14的剩余量P与时间t的函数关系式为,所以死亡生物组织内的碳14经过12个“半衰期”后的含量故选D。

变式2:为了预防流感,某学校对教室用药熏消毒法进行消毒。已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t的函数关系式为(a为常数),如图1所示。据图中提供的信息,回答下列问题:

图1

(1)从药物释放开始,每立方米空气中的含药量y(mg)与时间t(h)之间的函数关系式为____;

(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么,药物释放开始,至少需要经过____h后,学生才能回到教室。

解析:(1)由题意和图知,当0≤t≤0.1时,可设y=kt(k为待定系数),由于点(0.1,1)在直线上,所以k=10;同理,当t>0.1时,可得1=,解得所以

二、对数问题

里氏震级M的计算公式为M= lgA-lgA0,其中A是测震仪记录的地震曲线的最大振幅,A0是相应的标准地震的振幅。假设在一次地震中,地震仪记录的最大振幅是1000,此时标准地震的振幅为0.001,则此次地震的震级为____级;9级地震的最大振幅是5级地震的最大振幅的____倍。

解析:根据题意,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅为0.001,则震级M=lgA-lgA0= lg1000-lg0.001=3-(-3)=6。

点评:本题与人教A版必修1第66页例5有相同的背景,考查对数的运算法则,同时也提醒我们要有防范地震的意识。

三、近似计算问题

《算数书》竹简于上世纪80年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相承也。又以高乘之,三十六成一。该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式它实际上是将圆锥体积公式中的圆周率π近似取为3。那么近似公式V≈相当于将圆锥体积公式中的π近似取为( )。

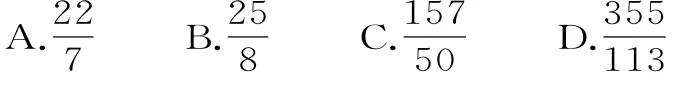
点评:本题是《算数书》中π的近似计算,与人教A版必修1第53页的不足近似值与过剩近似值的问题相似。通过练习本题,提醒我们应学习古代数学家刻苦钻研的精神。

四、导数问题

放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变。假设在放射性同位素铯137衰变过程中,其含量M(太贝克/年)与时间t(单位:年)满足函数关系:M(t)=,其中M0为t=0时铯137的含量,已知t=30时,铯137含量的变化率为-10ln2 (太贝克/年),则M(60)=( )。

A.5太贝克 B.75ln2太贝克C.150ln2太贝克 D.150太贝克

点评:本题通过放射性同位素铯137的衰变过程,考查导数的计算,求导函数的值。