论“单位涌水量就是导水系数”成立的特殊条件

王旭升，董岩岩

(中国地质大学(北京)水资源与环境学院, 北京 100083)

论“单位涌水量就是导水系数”成立的特殊条件

王旭升，董岩岩

(中国地质大学(北京)水资源与环境学院, 北京 100083)

针对截取侧向径流的抽水井，兰太权提出一个解释单位涌水量的公式，认为“单位涌水量就是导水系数”(q=T)，并以砂箱试验的结果作为证据。然而，这个等式的推导过程缺少严谨的水动力学基础。砂箱试验的边界条件等价于含有1个或2个定水头边界的矩形承压含水层，单井抽水的稳定流场可以用镜像井点叠加法求解，从理论上表明单位涌水量与导水系数成正比，而比例系数取决于含水层的形状和抽水井的半径。在特定条件下，含水层和抽水井的尺寸可以造成单位涌水量与导水系数相等的情况，兰太权发表于文献中的2组砂箱试验恰好符合这种条件，但并不能证明q=T具有普适性。新的砂箱试验避免了几何尺寸的这种特殊组合，得到了显著偏离q=T的结果。

抽水试验；单位涌水量；地下水动力学；导水系数

单井涌水量是目前水文地质勘探的基本成果，用于编制水文地质图，作为含水层“富水性”的一个指标。单井涌水量与抽水井水位降深的比值，又被称为单位涌水量，可用于粗略评估允许降深条件下的可开采量。由于抽水井的流量-水位关系涉及到比较复杂的井孔-含水层水动力学机理，对于单位涌水量如何取决于含水层的渗透系数和补给条件这个问题，尚无普遍适用而又简单的公式可以说明。现有关于单位涌水量的解释，多基于影响半径理想模型，适用范围很窄，对一些水文地质工作者产生了误导。

最近，兰太权[1]撰文认为传统径向稳定流理论对井孔抽水的动力学解释不合理，并重申他以往提出的“单位涌水量就是导水系数”这一观点。早在2004年，兰太权等[2]就发表文章讨论单位涌水量与含水层渗透系数的关系，介绍了1998年和1999年完成的2个砂箱试验，发现单位涌水量与含水层厚度的比值等于渗透系数。2007年，兰太权[3]仍然以该砂箱试验为证据，直接提出了“单位涌水量就是导水系数”的观点。

兰太权先生的论述有一个核心思想，即认为抽水井的动力学模型应该考虑普遍存在的天然侧向径流，而稳定状态的抽水流量等于抽水井截取的某个范围的径流量。通过引入“补给半径”及其定量假设[1, 3]，兰先生得到一个公式：

(1)

式中：q——抽水井的单位涌水量/(m2·d-1)；Qw——抽水井的流量/(m3·d-1)；sw——降深/m；T——导水系数/(m2·d-1)；K——含水层的渗透系数/(m·d-1)；M——含水层的厚度/m。

兰先生勇于提出问题挑战传统理论、主动进行试验探究的精神是值得称赞的。然而，式(1)并不具有普适意义，尽管兰先生自己做的砂箱试验似乎证明公式是正确的。这一点可以用已有的地下水动力学理论进行辨析。

本文的目的，是对兰先生提出的问题做出符合地下水动力学基本原理的解释，评论q=T成立的特殊条件，特别指出为什么某些砂箱试验似乎证明q=T是对的。井孔抽水的动力学理论已经是水文地质领域很成熟的基础科学，但是由于历史的原因，不少像兰先生这样的水文地质工作者仍然纠结于单井涌水量、单位涌水量这些概念与含水层参数的关系。实际上，从地下水动力学的角度来看，单位涌水量具有多解性[4]。笔者希望借助于对这个问题的评论，引发同行重视地下水动力学概念的科学理解和应用。

1 如何解释截取侧向径流的抽水井

兰先生认为传统的抽水井理论包含不符合实际的假设：假设存在以抽水井为中心的径向流；假设地下水的天然水位面是水平的。地下水普遍存在天然的水力坡度，具有倾斜水位面，抽水井对侧向径流产生截取作用，并不符合径向流特征。兰先生从上述角度对Dupuit模型等井流公式提出批判，出发点是合理的。从美国水文地质学家温策尔(Wenzer)报告的抽水试验结果(见文献[5])得到启发，他提出了考虑侧向径流的单井涌水量公式，即

Qw=2TCRbI

(2)

式(2)改写自文献[3]，其中I为地下水的天然水力坡度，而Rb和C都是他提出的新概念，分别被定义为“补给半径”及其控制范围内进入抽水井流量与总径流量的比例。进一步，兰先生假设Rb=sw/I以及C=1/2，从而推导出q=T，即式(1)。该式的前提条件是承压含水层完整井稳定流，也不考虑井损和井周扰动效应。为保持一致性，本文的讨论分析也基于这些限定。

只要仔细推敲兰先生的论述[1, 3]，可以判断其关于Rb和C的推测都是比较牵强的，并不具备可靠的动力学基础。然而，兰先生1998—1999年期间所做的砂箱试验数据[2～3]，似乎又表明式(1)没有错。那么，对于这种截取侧向径流的抽水井，经典地下水动力学能不能解释？会不会得到与兰太权公式一样的结论？针对这个问题，笔者在此提供2个严格的地下水动力学解析模型。

图1 承压含水层抽水井截取侧向径流的2种平面边界条件Fig.1 Two kinds of boundary conditions in the plan view for a pumping well capturing horizontal flow in a confined aquifer

如图1所示，有2种由定水头边界和隔水边界组成的矩形承压含水层可以采用砂箱试验进行模拟，在含水层内设置抽水井即可产生截取侧向径流的情况。图1(a)中有2条平行的定水头边界(一侧高一侧低)形成天然的侧向径流。图1(b)属于单个定水头边界的情况，抽水时间足够长就能够形成抽水井驱动的稳定流场。本文给出这2种情况是因为兰先生的论证涉及这些边界状态下的砂箱试验。如果是无限大的承压含水层或者四周只有隔水边界，则不可能形成稳定流。这一点前人早已证明[6～7]，而且也不可能用q=T来解释。因此，以下的分析都基于图1中所示的有限含水层。

首先解决图1(a)所示的模型。建立如图1(a)所示的坐标系，并且考虑抽水井在矩形含水层的形心位置这一特殊情况(兰先生的砂箱试验把放水孔至于形心位置)，则应用平面渗流理论的镜像对称井点叠加法[8]，可以得到任意坐标位置降深的解析解为：

(3)

式中：x,y——平面位置坐标；L——定水头边界之间的距离；D——隔水边界之间的距离；i——叠加的虚井序号。

把(x=0,y=rw)代入式(3)，则得到抽水井本身的理论降深为：

(4)

因此，单位涌水量与导水系数的关系可以表示为：

(5)

其中W1是图1(a)模型的井函数，由式(4)改写为：

(6)

同样采用平面渗流理论的镜像对称井点叠加法[8]，可以得到图1(b)所示模型的降深解析解为：

(7)

而抽水井单位涌水量与导水系数的关系表示为：

(8)

其中W2是图1(b)模型的井函数。把(x=0,y=rw)代入式(7)，单列i=0的级数项，合并i=0的级数项，对式(8)进行转换，则井函数W2可以展开为：

(9)

式(5)和(8)是上述2种边界条件的精确解，从水动力学上表明单位涌水量与导水系数成正比，但两者并不一定相等，比例系数取决于矩形含水层的形状尺寸和抽水井的半径。

2 公式q=T只适用于特例

在式(5)或(8)中，如果rw/L和D/L满足一些特定的组合，就会出现q=T的情况。兰先生1998—1999年期间进行的砂箱试验分为2步[3]。第1步将中间的放水孔关闭，保持一侧水头高(控制进水管)、另一侧水头低(控制排水管)，类似于图1(a)，形成稳定的侧向径流，把观测孔水位数据和流量数据代入Darcy定律，计算出填砂的渗透系数。第2步，打开中间的放水孔(模拟抽水井)，关闭下游排水管，等待流场调整到稳定状态，转变为图1(b)的情形，观测计算单位涌水量。因此，单位涌水量与导水系数的关系可以用式(8)进行描述。只要在制作砂箱的过程中，使rw、D、L三个几何参数满足特定的比例，导致W2=1，从而出现符合q=T的情况。这种特定组合可以用如图2所示的关系曲线来表示。

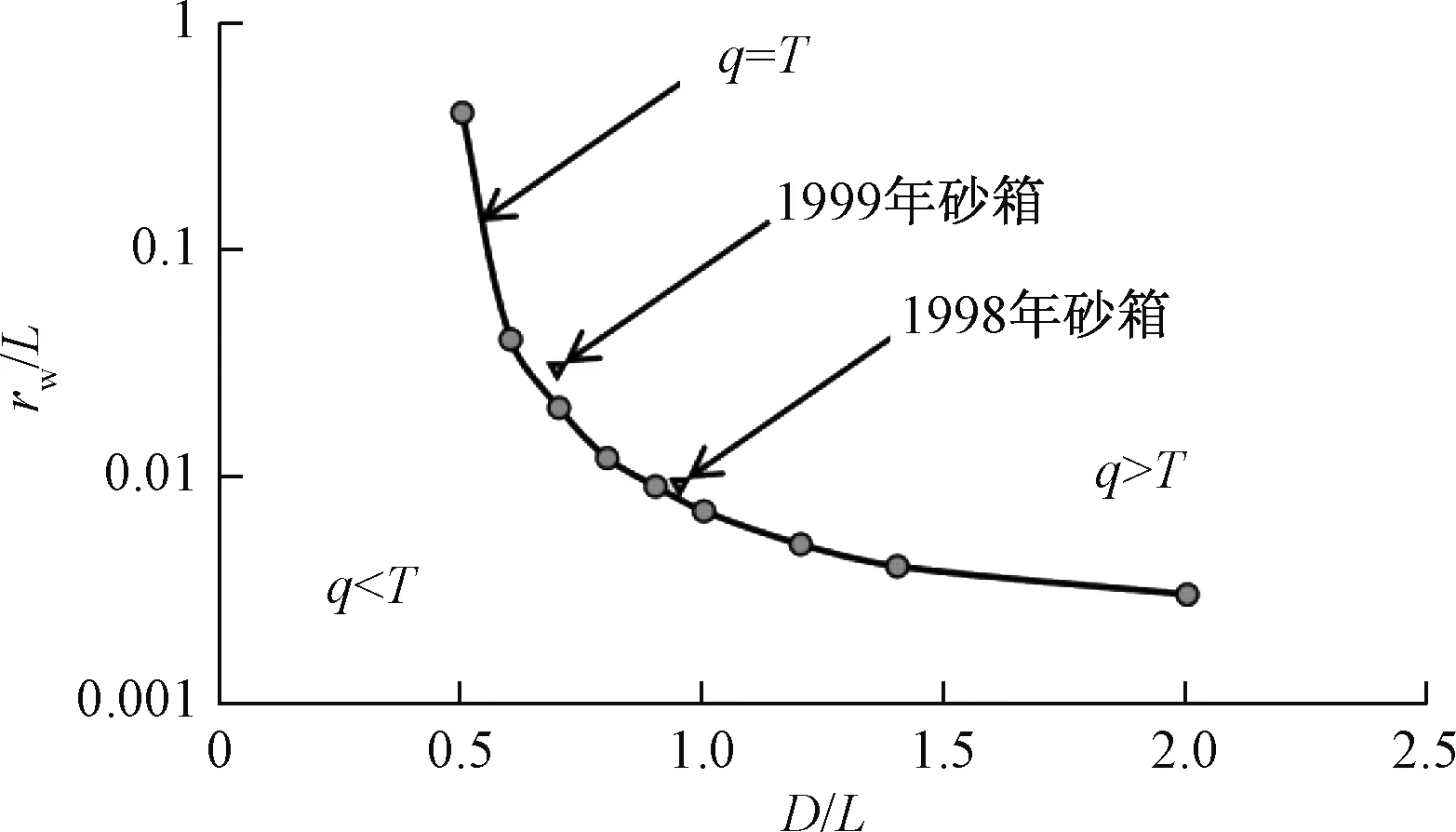
图2 根据式(8)确定的q=T成立条件曲线图Fig.2 The curve for conditions of q=T that determined with Eq. (8)

兰先生1998年试验砂箱的尺寸参数为：L=4.4 m，D=4.1 m，rw=3.81 cm(直径3 吋铁管)。兰先生1999年试验砂箱的尺寸参数为：L=1.4 m，D=0.98 m，rw=3.81 cm。这两个砂箱的几何参数恰好落在图2所示曲线的附近，因此基本上符合兰太权公式成立的条件。采用解析式(8)进行理论计算，可以证明：

q≈1.007T(1998年砂箱)

(10)

q≈1.044T(1999年砂箱)

(11)

也就是说，在兰先生1998—1999年的试验中由于砂箱尺寸和抽水孔半径满足上述特定条件，从而导致单位涌水量近似等于导水系数，理论误差都小于5%。其实，只要抽水孔半径在2.0～5.0 cm之间，这种“巧合”都会发生，因此兰先生发现q=T并不属于意外事件。

如果在砂箱试验的第2步中，保持下游侧的排水孔处于开放状态并固定水位，同时打开抽水孔，则试验条件将转变为图1(a)所示的情形。在这种边界条件下，要想让q=T成立，砂箱的尺寸和抽水孔的半径必须落在如图3所示的曲线上。显然，1998年砂箱和1999年砂箱都不能满足这个条件。因此，只要兰先生当初改变对下游排水孔的处理，就可以发现q>T的试验结果。然而，兰先生发表的文献中没有这种结果。

图3 根据式(5)确定的q=T成立条件曲线图Fig.3 The curve for conditions of q=T that determined with Eq. (5)

3 偏离q=T的砂箱试验

式(1)仅适用于特定条件，在砂箱试验中只要rw、D、L的数值不落在图2或图3的曲线附近，就不会产生q=T的结果。2015—2016年进行的2次砂箱试验证明了这一点。

2015年11月28日，笔者邀请兰先生到华北水利水电大学联合进行了一组砂箱试验，试验装置为一套模拟倾斜承压含水层的渗流槽，如图4所示。9个测压管均匀布置，与含水层顶板平行的间距为14.5 cm，依此可以计算各点间的水力梯度。放水孔直径1.5 cm，位于砂箱中部，与5号测压管连通。首先关闭放水孔进行了单向渗流试验，利用Darcy定律获得测压管间的渗透系数如表1所示，说明填砂不均匀，放水孔附近的导水系数为T=35～68 m2/d。此后打开放水孔进行了2次模拟抽水试验，结果见表1，获得单位涌水量q≈20 m2/d。显然，q相对T而言偏小40%以上，说明q=T并不成立。这次砂箱试验的边界条件类似于图1(a)，但由于填砂不均匀，无法用式(5)进行理论计算。

图4 华北水利电力大学砂箱试验装置示意图(2015年)Fig.4 Schematic of the sand box experimental system in the North China University Of Water Resources And Electric Power (2015)

2016年4月11日，笔者受兰先生邀请，到洛阳联合进行了新的砂箱试验。该砂箱由兰先生设计制作，铁皮封装竖直放置，如图5所示。填砂高度为L=0.94 m、宽度为D=0.60 m、等效含水层厚度M=0.40 m。为了考虑抽水井直径的影响，设置了2个放水孔：孔A位于砂箱中部，滤管半径rA=1.5 cm；孔B略偏离中部，滤管半径rB=1.0 cm。共进行了2次试验，每次首先进行Darcy渗流试验获得导水系数，然后分别进行孔A和B的放水试验，而排水管一直处于打开状态。

洛阳试验的数据见表2，可以看出第2次加大流量获取的导水系数比第1次大，可能是填砂受抽水试验扰动所致。两次试验中孔A和孔B的单井涌水量都大于导水系数，孔A结果偏大16%以上，孔B结果偏大12%以上。这样显著的偏差证明q=T是不成立的。对比孔A和孔B的结果还表明抽水井半径增大会导致单位涌水量也增大，这符合水动力学的理论判断。

表1 华北水利电力大学砂箱试验数据(2015年)Table 1 The data of sand box experiments in the North China University Of Water Resources And Electric Power (2015)

表2 洛阳砂箱试验数据(2016年)Table 2 The data of sand box experiments in the Luo Yang city (2016)

图5 洛阳砂箱试验装置照片和尺寸(2016年)Fig.5 The picture and size data of the sand box experimental system in the Luoyang city (2016)

洛阳砂箱试验的边界条件与图1(a)一致，因此可以用式(5)进行理论分析。把rA/L和D/L的数值代入式(5)，可以得到q/T=1.24，与孔A的试验结果(q/T=1.16～1.26)非常接近。如果假设孔B也位于中心处，把rB/L和D/L的数值代入式(5)得到q=1.15T，与孔B的试验结果(q/T=1.13～1.25)也相差不大。这说明用式(5)解释单位涌水量比用q=T更加准确。

需要进一步补充的是，以上砂箱试验基本上都把放水孔置于含水层的中心位置，试验结果具有特殊性。如果放水孔显著偏离中心位置，将会得到更加违反q=T的结果。例如，抽水井无限接近定水头边界时，单位涌水量将趋于无限大，显然不等于导水系数。这时式(5)和(8)也不再成立，需要使用更复杂的解析式，本文不予赘述。

4 结论

抽水井的单位涌水量与含水层的水文地质边界、水力学参数以及抽水井本身的特征都有关系。“单位涌水量等于导水系数”并不符合一般的地下水动力学条件。某些砂箱试验的结果符合q=T，是因为砂箱的几何形态和抽水孔的半径具有特定的组合关系，恰好导致单位涌水量等于导水系数，并不代表普遍的情况。本文给出了矩形承压含水层中心抽水稳定流场的解析解，证明这种情况下单位涌水量与导水系数成正比，而比例系数取决于含水层和抽水井的几何尺寸。只有在特定条件下，才会出现单位涌水量与导水系数相等的情况。实际的砂箱试验也证明q=T不具有普遍性。

如何解释单位涌水量与含水层参数的关系，的确是水文地质调查工作中需要解决的问题，但目前并没有普遍适用的简单公式。Dupuit公式由于包含“影响半径”这个模糊概念和忽略天然侧向径流，并不足以准确解释单位涌水量的动力学含义。兰太权先生认识到抽水井截取侧向径流的重要性，但关于单位涌水量等于导水系数的推论是不严谨的。采用符合实际条件的水动力学模型和非稳定流理论，并充分考虑抽水井的结构和开采方式，才是科学解释单位涌水量的必经之路。

致谢：感谢华北水利水电大学水工实验室提供2015年砂箱试验场地和赵静博士对试验工作的协助！兰太权先生在学术讨论过程中披露了早期砂箱试验的一些细节，陈崇希先生在水动力学分析上为笔者提出了宝贵的指导意见，在此表示感谢！

[1] 兰太权. 再论“单位涌水量就是导水系数”[J]. 水文地质工程地质, 2016, 43(5): 173-175.[LAN T Q. Revisit “the Specific Well Yield is the Transmissivity”[J].Hydrogeology &Geology Engineering,2016,43(5):173-175.(in Chinese) ]

[2] 兰太权, 赵安仁, 刘秋朝. 单位涌水量与渗透系数关系的探讨试验和应用[J]. 地下水, 2004, 26(1): 6-10.[LAN T Q, ZHAO A R, LIU Q C.Investigation experiments on the relationship between the specific capacity and hydraulic conductivity and application[J]. Ground Water, 2004, 26(1): 6-10. (in Chinese)]

[3] 兰太权. 论“单位涌水量就是导水系数”[J]. 地下水, 2007, 29(5): 43-45.[LAN T Q. A discussion on specific capacity and the transmissivity[J]. Ground Water, 2007, 29(5): 43-45. (in Chinese)]

[4] 张竞, 王旭升. 抽水井单位涌水量的多解性及应用[J]. 工程勘察, 2014(3): 33-37.[ZHANG J, WANG X S. Multiple solutions of specific capacity for pumping wells and their application[J]. Geotechnical Investigation & Surveying, 2014(3): 33-37. (in Chinese)]

[5] 张宏仁. 地下水水力学的发展[M]. 北京：地质出版社, 1992.[ZHANG H R. Development of groundwater hydraulics[M]. Beijing: Geological Publishing Press, 1992. (in Chinese)]

[6] 陈崇希. 地下水资源评价的原则和勘探思想的探讨[C]//地质矿产部水文地质工程地质研究所. 全国第一届地下水资源评价学术研讨会论文集. 北京:地质出版社, 1982:22- 33.[CHEN C X.On the principle of groundwater resource estimation and exploration ideas[C]// Institute of Hydrogeology and Engineering geology of Ministry of Geologyand Mineral Resources. The corpus of the first nationalproseminar on estimating of groundwater resources.Beijing: Geological Publishing Press, 1982:22-23. (in Chinese)]

[7] 陈崇希, 林敏. 地下水动力学[M]. 武汉：中国地质大学出版社, 1999.[CHEN C X, LIN M. Groundwater Dynamics[M]. Wuhan: China University of Geosciences Press, 1999: 66-69..(in Chinese)]

[8] 孔祥言. 高等渗流力学[M]. 合肥：中国科学技术大学出版社, 1999.[KONG X Y. Advanced mechanics of fluids in porous media[M]. Hefei: University of Science and Technology of China Press, 1999.(in Chinese)]

责任编辑：张若琳

《水文地质工程地质》征稿简则

《水文地质工程地质》1957年创刊，由国土资源部主管、中国地质环境监测院主办，是水文地质、工程地质、环境地质、地热地质专业领域综合性学术刊物之一。入选全国中文核心期刊(地质学)、中国科技核心期刊、中国科学引文数据库核心期刊，加入中国学术期刊光盘版。在国外检索系统中，被美国《化学文摘》(CAS)、美国《剑桥科学文摘》(CSA)、俄罗斯《文摘杂志》(AJ)等收录。

一 征稿范围

(1)水文地质、工程地质、环境地质、地热地质专业领域前沿研究成果，优先发表国家自然科学基金、国家重大基础研究项目、省部级科技创新基金资助的研究成果。

(2)学科边缘及学科交叉研究中的探索性成果。

(3)长期野外工作中取得的经验总结、建议。

二 征稿内容

水文地质：刊登渗流理论、水文地质参数计算、地下水数值模拟、地下水资源评价/开发利用/保护、水文地球化学、地下水污染机理与防治等方面的研究成果。

工程地质：刊登工程地质学科基础理论、重大工程场址稳定性、地(坝)基工程处理、岩土体物理力学参数、道路工程地质等方面的研究成果。

环境地质：刊登城市/矿山/农业环境地质、固体废物/废液/CO2处置、地质灾害形成机理与防治、荒漠化形成机理与防治、海岸带生态地质环境、水土地质环境等方面的研究成果。

地热地质：刊登地热资源勘查评价、资源量计算及数值模拟、地热资源利用及保护等方面的研究成果研究。三 稿件要求

(1) 论文题目明确、精练。

(2) 论文有项目资助的，应注明资助项目编号。

(3) 作者信息齐全：姓名(出生年-)，性别，职称，从事工作或研究方向、E-mail。

(4) 摘要简明扼要，说明论文目的、主要研究方法、研究结果和结论，英文摘要视具体情况可适当增加。中、英文对照关键词4～7个。

(5)论文需符合科研论文体裁，论点明确，论据充分，论述严谨，结论可信，语句通达，逻辑严密。

(6) 正文采用3级标题，即，一级标题如“2 模型建立及计算方法”；二级标题如“2.1 模型建立”；三级标题如“2.1.1 模型建立基本原则”或“(1)模型建立基本原则”。

(7)表格尽可能采用三线表，使用国家法定计量单位及其国际标准符号。中、英文表名齐全。

(8)图件尽量采用通用制图软件制作。单栏图件宽度不超过8cm，通栏图件宽度不超过15cm。图面内容重点突出、清晰、简明，图例内容与之一致，与正文中的说明一致。中、英文图名齐全。

(9) 全文字数一般不超过16 000汉字(8个版面，包括图、表)。

四 稿件录用

(1) 自收稿日起3个月内，通知作者论文处理结果。退稿不附详细意见。

(2) 作者收到修改通知后2个月内返回修改稿。逾期(特殊原因且已向编辑部说明者除外)视为自动撤稿。文责自负，请勿一稿多投。

(3) 录用稿件将酌收版面费，发表后按标准给付稿酬并赠送当期刊物。

五 投稿网址

www.swdzgcdz.com

·征订启事·

欢迎订阅《水文地质工程地质》

《中国地质灾害与防治学报》

《水文地质工程地质》由中华人民共和国国土资源部主管、中国地质环境监测院主办，1957年创刊，是我国水文地质、工程地质、环境地质专业领域创刊较早、发行较广，并具有权威性、综合性的学术理论与实践刊物之一。本刊入选全国中文核心期刊(地质学类)、中国科技核心期刊、中国科学引文数据库核心期刊，同时被美国《剑桥科学文摘》(CSA)、美国《化学文摘》(CA)、俄罗斯《文摘杂志》(AJ)等收录。主要栏目有水文地质、工程地质、环境地质、地热地质等。刊载水文地质、工程地质、环境地质、地质灾害、矿山地质环境、农业地质、城市地质、地热地质等学科具有较高学术水平的研究成果及新理论、新技术、新方法的应用与推广等。

《水文地质工程地质》为双月刊(每单月15日出版)，国际标准大16开本，每册定价30元，全年6期180元，合订本220元(含邮费)。本刊刊号：CN11-2202/P，ISSN1000-3665；邮发代号：2-335。广告许可证号：京海工商广字0265号。

《中国地质灾害与防治学报》由中华人民共和国国土资源部主管，中国地质环境监测院、中国地质灾害防治工程行业协会主办，1991年创刊。本刊为中国科学引文数据库来源期刊、中国核心期刊(遴选)数据库期刊，是我国工程地质、环境地质、地质灾害领域的综合性学术理论与实践的专业期刊，主要刊载由自然因素和人类经济活动诱发的崩塌、滑坡、泥石流、地面塌陷、地面沉降、地裂缝、矿井突水、岩爆、瓦斯爆炸、黄土湿陷、黏性土胀缩、冻土融陷、地下水污染、海水入侵、水土流失、土地沙漠化、盐渍化等地质灾害的发生发展机制、规律、监测、预报、防治新技术、新方法以及地质环境保护等具有较高学术水平的研究成果。面向国内工程地质学科发展、地质工程建设、技术方法创新、地质环境保护与开发等方面的科技人员。

《中国地质灾害与防治学报》为季刊(季末25日出版)，国际标准大16开本，每册定价30元，全年4期120元，合订本160元(含邮费)。本刊刊号：CN11-2852/P，ISSN1003-8035；邮发代号： 82-362。广告许可证号：京海工商广字0265号。

两刊皆兼营广告，欢迎广告惠顾。广大读者可通过邮局或编辑部订阅，通过编辑部订阅请在汇款单中注明“《水文地质工程地质》订刊款”或“《中国地质灾害与防治学报》订刊款”。

联系人：李善峰 电 话：(010)60850954 传 真：(010)60850957

联系地址：北京市海淀区大慧寺20号期刊编辑室 邮 编：100081

Discussions on the special conditions satisfying “the SpecificWell Yield is the Transmissivity”

WANG Xusheng, DONG Yanyan

(SchoolofWaterResources&Environment,ChinaUniversityofGeosciences,Beijing100083,China)

To interpret the meaning of the specific capacity of a pumping well capturing lateral groundwater flow, Lan (2007) proposed an equation where the specific capacity is equal to the transmissivity(q=T) and shown evidences from hydraulic tests in sand boxes. However, the derivation of this equation was not on the robust basis of groundwater hydraulics. The boundary conditions of the sand-box tests were equivalent to a rectangular confined aquifer with one or two constant head boundaries. The steady state flow driven by a pumping well in these conditions could be solved with the superposition method on imaging wells. It reveals that the specific capacity is proportional to the transmissivity and the coefficient is subject to the aquifer shape and the radius of the pumping well. In some conditions,q=Tcould be caused by the special geometric characteristics of the aquifer-well system. The hydraulic tests in sand boxes presented in Lan (2007) just satisfied such special conditions but did not indicate thatq=Tis generally applicable. New tests in sand boxes without these special geometric characteristics have shown significant different results from theq=Tequation.

pumping tests; specific capacity; groundwater hydraulics; transmissivity

2017-01-14;

2017-02-10

王旭升(1974-)，男，教授，博士生导师，主要从事水文地质方面的教学和科研工作。E-mail: wxsh@cugb.edu.cn

10.16030/j.cnki.issn.1000-3665.2017.03.24

P641.2

A

1000-3665(2017)03-0165-06