软岩非线性蠕变损伤模型及其试验研究

黄海峰，巨能攀，黄 敏，张成强，朱俊霖

(成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

软岩非线性蠕变损伤模型及其试验研究

黄海峰，巨能攀，黄 敏，张成强，朱俊霖

(成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

为了反映软岩蠕变全过程，进行红层泥岩蠕变力学试验，试验发现弹性模量随时间的增长而逐渐衰减，黏滞系数在应力恒定且并未达到屈服应力的情况下，随时间的增长而逐渐增大。因此认为传统理论流变力学中的蠕变损伤处理方法不适用于将黏滞系数进行损伤演化，故引入分数阶微积分来描述软岩蠕变的黏弹性和黏塑性应变。通过构建一个考虑蠕变时效损伤的弹性体，并将其与基于分数阶微积分的黏滞和黏塑性体进行串联，从而建立一个新的非线性蠕变损伤模型。依据红层泥岩和相关文献中冻结软岩及红砂岩的蠕变试验数据，通过该软岩蠕变损伤模型对其进行辨识，充分显示出所建模型的合理性和适用性。

蠕变；弹性模量；黏滞系数；蠕变损伤模型；分数阶微积分

蠕变特性是岩体重要的力学特性之一，与岩石工程长期稳定性密切关联[1～3]。前人依据本构关系组合简单蠕变元件，建立了大量蠕变本构模型。其中绝大部分蠕变本构模型中的力学参数是定常的，认为这些力学参数无时效性[4～5]，但实际上，岩石这种复杂的材料在地质构造运动、自然风化和水岩作用等诸多因素作用下，经受温度和压力而导致岩石材料的性能劣化(包括强度、弹性模量等的降低)，引起材料性能劣化的微结构变化即为损伤[6]。若通过采用流变损伤力学的研究方法，借助引入损伤变量，在某种意义上可表征岩石材料的性能劣化过程，同时也可体现岩石材料的损伤演化过程。不少学者通过经典和非经典的黏弹塑性理论以及损伤力学理论建立了蠕变损伤本构模型。Chan等[7～8]提出了一种可以较好地描述盐岩蠕变损伤特性的蠕变、损伤和断裂多机制耦合模型；朱昌星等[9]通过对时效损伤和损伤应力阈值的研究，基于黏弹塑性理论构建了非线性蠕变损伤模型；赵延林等[10]将传统伯格斯模型和非线性M-C塑性元件串联，建立了一个新的BNMC蠕变损伤模型，并验证该模型模拟岩石的黏弹塑性偏量特性和蠕变损伤的合理性。

本文试验发现，红层泥岩蠕变全过程中黏滞系数并未随时间的增长而持续减小，在应力恒定且并未达到屈服应力的情况下，黏滞系数随时间的增长而增大。传统理论流变力学模型中的蠕变损伤处理方法一般是直接将蠕变方程中的表观应力替换成等效应力，实际上等同于将蠕变方程中的流变参数p改为随时间演化的参数p(1-D)。尽管本文试验发现红层泥岩在蠕变过程中弹性模量随着时间的增长而递减，但是黏滞系数并未随着时间的增长而一直递减。因此本文的蠕变损伤模型在损伤力学理论的基础上引入分数阶微积分，对于弹性应变基于损伤力学理论进行辨识，对于黏弹性应变和黏塑性应变利用分数阶微积分进行辨识，建立一个能够较为全面地反映软岩蠕变机制的非线性蠕变损伤模型，并验证所建模型的合理性和正确性。

1 蠕变试验说明

蠕变试验采用YSJ-01-00岩石流变试验机(图1)，使用逐级增量加载的试验方式。取样地点为四川省新津县狮子山边坡(狮子山边坡是具有较强蠕滑现象的红层边坡)，于边坡后缘削坡取出新鲜泥岩试样后密封运回实验室，加工成φ50 mm×100 mm的圆柱样，依据滑带深度将围压设置为1 MPa，每级轴向荷载增量Δq=Kqf/n，其中K为材料的强度降低系数，据经验取0.65～0.85。共施加6级轴向荷载，对应应力为1～6 MPa，试验共历时1 251 h。图2为利用Boltzmann线性叠加原理对原始数据处理后的分别加载蠕变曲线，图3为等时应力-应变曲线，图4为弹性模量损伤衰减曲线。

图1 试验仪器Fig.1 Diagram showing the test instrument

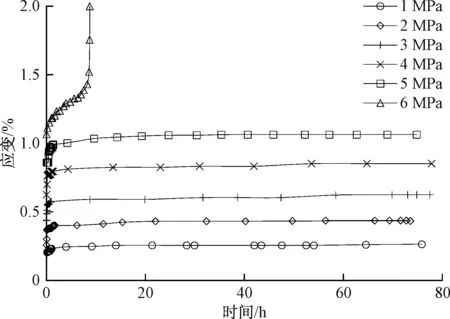
图2 分别加载蠕变曲线Fig.2 Separate loading creep curves

图3 等时应力—应变曲线Fig.3 Isochronous stress-strain curves

图4 弹性模量损伤衰减曲线Fig.4 Elastic modulus damage attenuation curve

2 蠕变损伤分析

2.1 损伤变量的定义

根据损伤力学理论，采用能量损伤中按弹性模量变化[11]定义的方法，认为工程岩体在初始状态下的弹性模量为E0，受扰动后，弹性模量逐渐衰减直至一个稳定值。由图4可知，弹性模量E(t)向长期弹性模量E∞逐渐衰减，由此定义两种状态：(1)当t=0时，损伤变量D=0，此时材料无损；(2)当t→∞，损伤变量D=1，此时材料完全损伤。当时间t逐渐增长时，损伤变量D逐渐趋于1。故建立如下损伤演化方程：

(1)

式中:δ——与损伤程度相关的系数；E0——初始弹性模量；E∞——长期弹性模量。

假设材料为各向同性损伤，则E(t)可表示为：

(2)

Kachanov[1]认为在一维应力状态下，蠕变条件下的损伤发展方程为：

(3)

式中：A，ν——材料参数；σ——应力。

对式(3)进行积分可得蠕变破坏时间te为：

(4)

联立式(3)和式(4)可得D的演化规律为：

(5)

2.2 考虑岩石蠕变时效损伤的弹性体

大量的试验和理论研究表明，当应力超过损伤应力阈值(即屈服应力)，岩石材料才能进入加速蠕变阶段，岩石材料才会随着时间产生损伤[11～12]。本文认为应力水平未达损伤应力阈值时，岩石蠕变无损伤。无损状态的岩石材料，对于瞬时加载的响应是弹性的，可用虎克体描述其弹性应变εe：

(6)

当应力超过损伤应力阈值时，根据Lemitre 等效应力原理[13]，将式(2)代入式(6)可得：

(7)

再将式(5)与式(7)联立可得：

(8)

式(8)即为应力超过损伤应力阈值时的考虑时效损伤的弹性体的本构方程。

3 基于分数阶微积分的黏滞体和黏塑性体

3.1 分数阶微积分的引入

孙钧[1]、范庆忠等[14]认为，软岩在低应力作用下衰减蠕变变形向高应力作用下加速蠕变变形发展的整个过程中，黏滞系数η在某种条件下随时间增大。实际上，本文试验发现，黏滞系数η随应力的增大而减小，但在应力未达到屈服应力的情况下，应力恒定时，黏滞系数η随时间的增长而递增。不同时刻和不同应力的黏滞系数值如表1和图5所示。

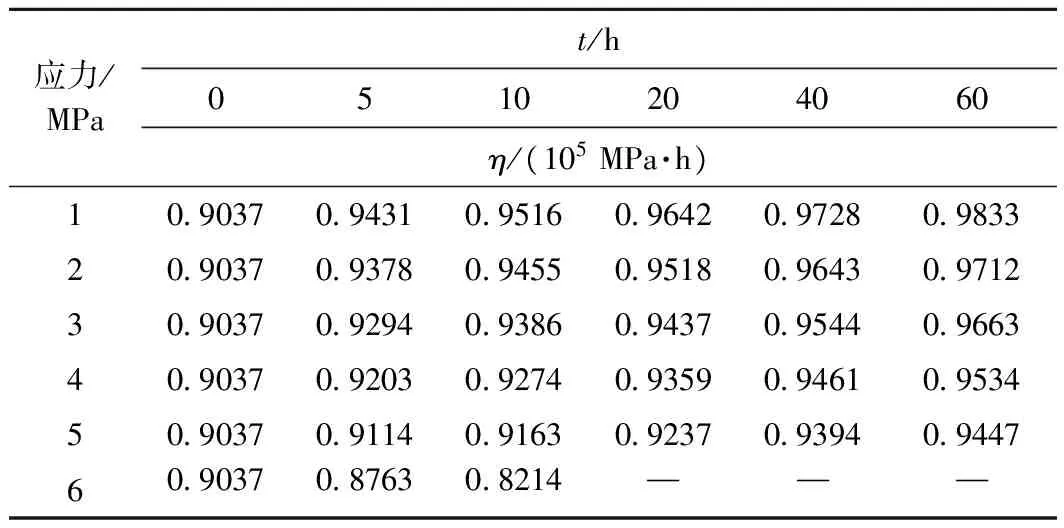
表1 黏滞系数值Table 1 Viscosity coefficient

传统理论流变力学模型中的蠕变损伤处理方法一般是直接将蠕变方程中的表观应力替换成等效应力，实际上等同于将蠕变方程中的流变参数p改为随时间演化的参数p(1-D)，若将黏滞系数η改为η(1-D)明显是不合理的。由此，将物理意义更清晰、表述更简洁的分数阶微积分引入到红层泥岩蠕变损伤模型中。

3.2 基于分数阶微积分的黏滞体

分数阶微积分有多种定义方法，目前岩石流变本构研究中最受认可的是利用Riemann-Liouville理论[15～16]进行定义。依该理论，函数f(t)在区间[α，+∞)上α阶可积，则f(t)的Riemann-Liouville分数阶导数定义为：

(9)

m=[α]

式中：m-α——分数阶阶数。

Gamma函数可表示为：

(10)

(11)

实际上，岩石材料被认为是一种介于理想固体和理想流体之间的材料，参考Scott-Blair等[17]引入一个用来描述理想固体和理想流体之间某种状态的软体元件，即本文的分数阶黏滞体，其本构为：

(12)

当α=0时，该分数阶黏滞体可描述理想固体；当α=1时，该分数阶黏滞体可描述理想流体；当0<α<1时，该分数阶黏滞体可描述介于理想固体和理想流体之间如岩石材料等的变形情况。

当σ=const时，基于Riemann-Liouville型分数阶微积分理论，将式(12)进行分数阶积分可得：

(13)

式(13)即分数阶黏滞体的蠕变本构方程。

图6 分数阶黏滞体蠕变曲线Fig.6 Creep curves of fractional viscous body

3.3 基于分数阶微积分的黏塑性体

一般认为，当应力超过屈服应力σL时，才会产生黏塑性应变[18～20]。本文采用非线性黏塑性体来描述黏塑性应变εvp。该黏塑性体的总应力可表示为：

(14)

式中：σn——黏滞体中的应力。

σs定义为：

(15)

由于当应力超过屈服应力时，才会产生黏塑性应变，故当σ<σL时，εvp=0。

当σ≥σL时，黏塑性体中的总应力σ为：

(16)

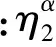
基于 Riemann-Liouville型分数阶微积分理论，对式(16)进行分数阶积分可得：

(17)

4 非线性蠕变损伤模型及模型验证

4.1 模型建立

依据前面对考虑岩石蠕变时效损伤的弹性体和基于分数阶微积分的黏滞体、黏塑性体的分析，该弹性体可描述泥岩蠕变的弹性应变，该黏滞体可描述其黏弹性应变，该黏塑性体可描述其黏塑性应变，将该弹性体、黏滞体和黏塑性体串联，建立一个3元件的非线性蠕变损伤模型(图7)。

图7 非线性蠕变损伤本构模型Fig.7 Nonlinear creep damage constitutive model

假定当t=0时，对该模型施加瞬时恒定应力σ0，则模型总应变ε=εe+εve+εvp，结合式(6)，(8)，(13)，(17)有：

(18)

式(18)即为本文软岩非线性蠕变损伤模型的本构方程。

4.2 模型验证及参数求解

参数拟合用一般的非线性最小二乘拟合就可以得到，基于Levenberg-Marquardt算法，通过本文试验数据对所建模型拟合效果进行验证。红层泥岩蠕变

试验值与拟合值对比曲线见图8，蠕变损伤模型参数见表2。

图8 红层泥岩蠕变试验值与拟合值对比曲线Fig.8 Comparison curves of the test and fitting values of the red mudstone

岩石材料应力/MPaE0/MPaη1/(GPa·h)η2/(GPa·h)AναR2189612877———0060994528057614———00709926红层泥岩37243822———0070991746752198———0050988756111421———008097946589673455302×10-410601209892243273958264———00909934冻结软岩282446340198———01109871321213322217———0190991145885964653075283×10-6223603509903280371456121741———0140983533635362898537———01809767红砂岩39244162741454———0150990544844013340331———027098445045233163557412715866×10-7582804709918

为了验证本文模型对于软岩蠕变曲线和参数辨识的合理性和适用性，利用本文模型对文献[3,21]中的白垩系冻结软岩、红砂岩的蠕变数据进行辨识。试验值与拟合值对比曲线见图9，相关的模型参数见表2。由图8、图9和表2可看出，拟合曲线与试验数据吻合较好，误差较小，对于不同软岩不同形态的蠕变全过程的拟合效果较好，本文蠕变模型能够较为准确地辨识软岩蠕变全过程。

图9 冻结软岩、红砂岩试验值与拟合值对比曲线Fig.9 Comparison curves of the test and fitting values of the frozen soft rock and red sandstone

5 结论

(1)依据损伤力学理论，引入Kachanov蠕变率，建立一个在蠕变损伤过程中考虑时效损伤的弹性体。通过本文试验结果发现，在应力恒定且并未达到屈服应力的情况下，黏滞系数随时间的增长而递增。因此认为传统理论流变力学中的蠕变损伤处理方法不适用于黏滞系数，故引入物理意义清晰、结构简单的分数阶微积分来定义黏滞体和黏塑性体，由此构建一个能较为准确地辨识软岩蠕变全过程的非线性蠕变损伤模型。

(2)根据本文红层泥岩蠕变试验结果和相关文献中红砂岩及盐岩的蠕变试验数据，对所建模型进行参数求解，并对比拟合曲线与试验数据，验证了本文所建模型对于辨识软岩蠕变全过程的合理性和适用性。

(3)所建模型拟合曲线较为灵活，参数相对较少，对于不同软岩蠕变全过程(尤其是加速蠕变阶段)的辨识效果较好，便于应用。

本文蠕变试验背景为具有较强蠕滑特性的红层边坡，依据红层泥岩的蠕变试验成果建立该蠕变损伤模型，所建模型对红层边坡的长期稳定性研究及监测预警提供一定参考。

[1] 孙钧. 岩土材料流变及其工程应用[M]. 北京: 中国建筑工业出版社, 1999. [SUN J. Rheology of geo-material and its engineering application[M]. Beijing: China Architecture and Building Press, 1999.(in Chinese)]

[2] 刘正, 高文华, 刘栋,等. 深部围岩流变特性试验研究及其模型辨识[J]. 水文地质工程地质, 2012, 39(4):43-48. [LIU Z, GAO W H, LIU D,etal. An experimental study of the creep properties of deep surrounding rocks and creep model identification[J]. Hydrogeology & Engineering Geology, 2012, 39(4):43-48. (in Chinese)]

[3] 李栋伟, 汪仁和, 范菊红. 白垩系冻结软岩非线性流变模型试验研究[J]. 岩土工程学报, 2011, 33(3):398-403. [LI D W, WANG R H, FAN J H. Nonlinear rheological model for frozen soft rock during Cretaceous period[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(3):398-403. (in Chinese)]

[4] Ping C, Wen Y, Wang Y,etal. Study on nonlinear damage creep constitutive model for high-stress soft rock[J]. Environmental Earth Sciences, 2016, 75(10):1-8.

[5] Günther R M, Salzer K, Popp T,etal. Steady-State Creep of Rock Salt: Improved Approaches for Lab Determination and Modelling[J]. Rock Mechanics and Rock Engineering, 2015, 48(6):2603-2613.

[6] Zhou K P, Bin L I, Jie-Lin L I,etal. Microscopic damage and dynamic mechanical properties of rock under freeze-thaw environment[J]. Transactions of Nonferrous Metals Society of China, 2015, 25(4):1254-1261.

[7] Chan K S, Bodner S R, Fossum A F,etal. A Damage Mechanics Treatment of Creep Failure in Rock Salt[J]. International Journal of Damage Mechanics, 1997, 6(2):121-152.

[8] Chan K S, Bodner S R, Fossum A F,etal. Inelastic Flow Behavior of Argillaceous Salt[J]. International Journal of Damage Mechanics, 1996, 5(5):292-314.

[9] 朱昌星, 阮怀宁, 朱珍德, 等. 岩石非线性蠕变损伤模型的研究[J]. 岩土工程学报, 2008, 30(10):1510-1513. [ZHU C X, RUAN H N, ZHU Z D,etal. Non-linear rheological damage model of rock[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10):1510-1513. (in Chinese)]

[10] 赵延林, 唐劲舟, 付成成, 等. 岩石黏弹塑性应变分离的流变试验与蠕变损伤模型[J]. 岩石力学与工程学报, 2016, 35(7):1297-1308.[ZHAO Y L, TANG J Z, FU C C,etal. Rheological test of separation between viscoelastic-plastic strains and creep damage model[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7):1297-1308. (in Chinese)]

[11] 张强勇, 杨文东, 张建国, 等. 变参数蠕变损伤本构模型及其工程应用[J]. 岩石力学与工程学报, 2009, 28(4):732-739.[ZHANG Q Y, YANG W D, ZHANG J G,etal. Variable parameters-based creep damage constitutive model and its engineering application[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(4):732-739. (in Chinese)]

[12] 宋勇军, 雷胜友, 刘向科. 基于硬化和损伤效应的岩石非线性蠕变模型[J]. 煤炭学报, 2012, 37(增刊2):287-292.[SONG Y J, LEI S Y, LIU X K. Non-linear rock creep model based on hardening and damage effect[J]. Journal of China Coal Society, 2012, 37(Sup 2):287-292. (in Chinese)][13] 金磊, 夏才初. 理论流变力学模型中蠕变损伤的研究方法与问题[J]. 岩石力学与工程学报, 2012, 31(增刊1):3006-3014.[JIN L, XIA C C. Study methods for creep damage in theoretical rheological models and some problems[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(Sup 1):3006-3014. (in Chinese)]

[14] 范庆忠, 高延法, 崔希海, 等. 软岩非线性蠕变模型研究[J]. 岩土工程学报, 2007, 29(4):505-509.[FAN Q Z, GAO Y F, CUI X H,etal. Study on nonlinear creep model of soft rock[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(4):505-509. (in Chinese)]

[15] Adolfsson K, Enelund M, Olsson P. On the Fractional Order Model of Viscoelasticity[J]. Mechanics of Time-Dependent Materials, 2005, 9(1):15-34.

[16] Zhou H W, Wang C P, Han B B,etal. A creep constitutive model for salt rock based on fractional derivatives[J]. International Journal of Rock Mechanics & Mining Sciences, 2011, 48(1):116-121.

[17] Blair G W S. Analytical and Integrative Aspects of the Stress-Strain-Time Problem[J]. Journal of Scientific Instruments, 1944, 21(5):80-84.

[18] 巨能攀, 黄海峰, 郑达, 等. 考虑含水率的红层泥岩蠕变特性及改进伯格斯模型[J]. 岩土力学,2016, 37(增刊2):67-74.[JU N P, HUANG H F, ZHENG D,etal. Improved Burgers model for creep characteristics of red bed mudstone considering water content[J]. Rock and Soil Mechanics, 2016, 37(Sup 2):67-74. (in Chinese)]

[19] 毕港, 韦健飞, 黄梦昌,等. 土体蠕变的新模型[J]. 水文地质工程地质, 2016, 43(6):53-58.[BI G, WEI J F, HUANG M C,etal. A new model for soil creep[J]. Hydrogeology & Engineering Geology, 2016, 43(6): 53-58. (in Chinese)]

[20] 唐皓, 赵法锁, 段钊,等. 基于分数阶微积分改进的黄土西原模型[J]. 水文地质工程地质, 2014, 41(5):50-56. [TANG H, ZHAO F S, DUAN Z,etal. The improved Nishihara model of loess based on fractional calculus [J]. Hydrogeology & Engineering Geology, 2014, 41(5): 50-56. (in Chinese)]

[21] 赵宝云, 刘东燕, 郑颖人,等. 红砂岩单轴压缩蠕变试验及模型研究[J]. 采矿与安全工程学报, 2013, 30(5):744-747.[ZHAO B Y, LIU D Y, ZHENG Y R,etal. Uniaxial compressive creep test of red sandstone and its constitutive model[J]. Journal of Mining & Safety Engineering, 2013, 30(5):744-747. (in Chinese)]

责任编辑：张明霞

Nonlinear creep damage model of soft rock and its experimental study

HUANG Haifeng, JU Nengpan, HUANG Min, ZHANG Chengqiang, ZHU Junlin

(StateKeyLaboratoryofGeohazardPreventionandGeoenvironmentProtection，ChengduUniversityofTechnology，Chengdu，Sichuan610059,China)

In order to reflect the whole process of soft rock creep, the red mudstone creep experiment is carried out. The experimental results show that the elastic modulus gradually decreases with the increasing time and the viscosity coefficient gradually increases with the increasing time under the constant stress before yield. Therefore, this paper argues that the processing method of creep damage in the traditional theoretical rheology is not applicable to the damage evolution of the viscous coefficient, and the fractional calculus is used to describe the viscoelastic and viscoplastic strain of soft rock creep. By constructing an elastic body based on time-dependent damage, which is in series with a viscous body and a viscoplastic body based on fractional calculus, a new nonlinear creep damage model is established. The creep test data of red mudstone, frozen soft rock and red sandstone are identified with the creep damage model of soft rock, and the rationality and applicability of the proposed model is shown.

creep; elastic modulus; viscosity coefficient; creep damage model; fractional calculus

2016-12-20;

2017-01-17

国家自然科学基金项目资助(41372306)

黄海峰(1993-)，男，硕士研究生，主要从事岩土体稳定性及工程环境效应研究。E-mail：651045475@qq.com

巨能攀(1973-)，男，博士，教授，博导，主要从事岩质高边坡和灾害监测预警的研究。E-mail：jnp@cdut.edu.cn

10.16030/j.cnki.issn.1000-3665.2017.03.08

：TU458+.3

A

1000-3665(2017)03-0049-06