考虑弹性模量变化的岩石统计损伤本构模型

曹文贵，杨 尚，张 超

(湖南大学岩土工程研究所，湖南 长沙 410082)

考虑弹性模量变化的岩石统计损伤本构模型

曹文贵，杨 尚，张 超

(湖南大学岩土工程研究所，湖南 长沙 410082)

为建立更为完善的岩石统计损伤本构模型，针对现有模型难以反映某些岩石在三轴试验条件下弹性模量随围压变化而改变的特性，从不同类型空隙对岩石变形性质的影响入手，深入分析了岩石弹性模量变化的机理，并在此基础上，依据弹性参数与岩石中未闭合裂隙数的关系建立了岩石弹性模量变化的分析方法。之后，引入统计损伤理论，考虑损伤阈值的影响和残余强度变形特征，建立了可模拟岩石变形全过程的统计损伤本构模型，并给出了基于三轴压缩试验曲线的模型参数确定方法。本文模型可反映岩石弹性模量随围压变化而改变的特性，且具备现有模型的优点，对岩石变形全过程模拟效果良好。最后，通过试验曲线与本文及同类模型理论曲线的对比分析，表明了本文模型的合理性与优越性。

弹性模量变化；损伤阈值；残余强度；统计损伤；本构模型

岩石本构模型也即变形全过程模拟是岩石力学研究的基础和重要内容，众多学者对此进行了深入的研究，取得了长足的进展和丰硕的成果，其中基于统计损伤理论的本构模型尤为成功。但是，这些模型具有一个共同的不足，即无法反映某些岩石(如砂岩等)弹性模量随三轴压缩试验中围压的变化而改变的特性。因此，有必要开展进一步的研究，以发展和完善模拟岩石变形破坏全过程的统计损伤本构模型。

自唐春安等[1]将统计损伤理论引入到岩石变形全过程模拟以来，诸多学者循着这一思路开展了广泛而深入的研究，取得的成果可反映岩石变形破坏全过程许多方面的特性，如损伤阈值对变形过程的影响[2]、岩石应变软硬化特性[3～4]、峰值强度与围压的关系[5～6]、岩石破坏的脆-延特性转化[7]以及完全破坏后存在残余强度的变形特征[8～9]等。但是，这些模型都不能反映岩石弹性模量随围压变化而改变的特性[10～12]。究其原因，一直以来，屈服破坏前的岩石都被视为是致密的材料，因而其应力应变关系必然服从广义Hooke定律，且弹性模量为常数。事实上，岩石中不可避免地会包含许多初始空隙[13]，随着压力的增大，这些空隙会逐渐闭合，从而引起岩石变形性质的改变，也即弹性模量的变化。

由以上分析可以发现，虽然目前基于统计损伤理论的岩石本构模型[2～5,7～9]具有某些缺陷，但是，这并非是统计损伤理论自身的不足，而是由于建立本构模型时考虑的因素不够周全，致使所建立的模型无法反映岩石变形破坏全过程中的某些特性。而且统计损伤理论确实为岩石变形全过程模拟方法研究提供了一条合理且行之有效的途径。因此，本文仍将以统计损伤理论为基础，重点探讨如何改进和完善岩石统计损伤本构模型。

为使建立的统计损伤本构模型能够反映岩石弹性模量随围压变化而改变的特性且具备现有相关模型的优点，本文将首先探讨不同围压下岩石弹性模量变化及变形全过程的特点，并由不同类型空隙对于岩石变形性质的影响角度入手，深入分析岩石弹性模量变化的机理。在此基础上，引入统计损伤理论，开展对于岩石变形全过程模拟方法的进一步研究，并汲取现有相关研究成果的优点，以期建立的岩石统计损伤本构模型不仅能够反映岩石应变软化特性和残余强度变形特征，且能够对岩石弹性模量变化的特性做出较好模拟，以发展并完善岩石统计损伤本构关系研究。

1 岩石弹性模量变化及变形全过程特点

由不同围压下岩石三轴压缩试验曲线(图1)可以发现：

(1)不同围压下岩石变形破坏全过程曲线表现为相似的阶段性特征，即岩石受到应力后都会出现线性变形阶段、应变硬化段、应变软化段，直至完全破坏，岩石所能承受的应力维持为一个稳定值，即残余强度[8～9]。

(2)在线性变形阶段，岩石应力应变曲线斜率也即岩石弹性模量会随围压的增大而逐渐增大，直至达到最大值，之后，即使围压继续增大，岩石弹性模量也不再改变[10～12]。

图1 岩石弹性模量变化及变形全过程Fig.1 The variation of rock elastic modulus and complete deformation process for rocks

岩石变形破坏全过程曲线出现应变硬化和软化以及残余强度变形阶段是由于岩石屈服之后损伤的发生和不断演化，可由统计损伤理论分析模拟[8,9]；而线性变形阶段曲线斜率也即岩石弹性模量随围压变化而改变则是由岩石中空隙随着围压增大而逐渐闭合引起的。为建立岩石弹性模量变化分析模型，首先需要深入分析岩石中空隙对变形性质的影响。

2 空隙对岩石变形性质的影响

岩石中的空隙可依据其形状分为孔隙和裂隙两类[13]，孔隙是指球形或近似于球形的空隙，而裂隙指岩石中狭长的裂缝。如果定义纵横比η表示空隙最小直径与最大直径的比值，则孔隙的纵横比接近于1，而裂隙的纵横比远小于1。两类空隙的几何情况不同，其对岩石变形性质的影响也必然会存在很大差异。

由文献[13,14]，如果假定岩石中的空隙均为硬币形(penny shape)椭圆空隙(即空隙三个轴的长度分别为2a，2a和2ηa，a称为空隙半长度)，且所有空隙的半长度都相等，空隙之间的区别仅在于纵横比不同，则当包含空隙的岩石受到大小为p的静水压力作用之后，有：

(1)

式中：Es，μs——岩石骨架的弹性模量和泊松比，一般可认为是常数；

η0——空隙的初始纵横比；

η——岩石受到p作用后的纵横比。

当空隙刚好完全闭合(即η=0)，此时的静水压力称为该空隙的闭合压力，如果以pcl表示，则有：

(2)

由式(2)即可分析孔隙和裂隙对岩石变形性质的不同影响。对孔隙而言，其初始纵横比η0接近于1，因而闭合压力pcl约为πEs/[4(1-μs2)]。一般而言，该值大小与地球内部地幔与地核交界处的压力相当，因此，地表工程压力对孔隙的压缩是极其微小的，可以认为孔隙并不会变形，自然也就不会引起岩石弹性参数的变化[13]。而裂隙则大不相同，其初始纵横比大多在10-3～10-4之间，因而在几十兆帕的压力下裂隙会逐渐闭合，从而引起岩石弹性参数的变化[13]。对于仅包含裂隙的岩石，裂隙对岩石变形性质的影响可表示为[13～14]：

(3)

式中：β，V——岩石的体积柔量和体积；N——岩石中未闭合的裂隙数；βs——岩石骨架的体积柔量。

又由弹性理论[13]有：

(4)

(5)

式中：K，μ，E——岩石的体积模量、泊松比和弹性模量；

Ks——岩石骨架的体积模量。

如果忽略泊松比变化的影响(即认为μ=μs)，则将式(4)和式(5)代入到式(3)可得：

(6)

式(6)中a不会随压力的增减而发生变化[13～14]，如果忽略岩石体积的变化，认为V为常数，则岩石弹性模量仅与其中未闭合裂隙数有关。容易发现，随着压力的增加，岩石中裂隙会逐渐闭合，即未闭合裂隙数N逐渐减小，从而使得岩石弹性模量逐渐增大，当岩石内裂隙全部闭合，即N=0，则有E=Es，岩石弹性模量达到最大值，之后，即使压力继续增大，弹性模量也不会再变化。

以上即为空隙对岩石变形性质的影响及岩石弹性模量变化的机理，在此基础上即可建立岩石弹性模量变化的分析模型。

3 岩石弹性模量变化分析模型

由前述分析，岩石弹性模量变化仅与岩石中未闭合裂隙数的改变有关，因此，要建立岩石弹性模量变化的分析模型，首先需解决岩石中未闭合裂隙数如何随压力增大而变化的问题。而式(2)表示岩石中裂隙只会在各向等压的静水压力作用下才会闭合从而引起未闭合裂隙数的变化，由此，本文将静水压力近似视为最小主应力σ3，则式(2)也可表示为：

(7)

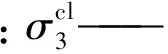
如果岩石中初始裂隙数为N0，这N0条裂隙的初始纵横比互不相等且可按照由小到大的顺序排列为η1，η2，…，ηi，…，ηN0，并假定这N0条裂隙的初始纵横比在[0，ηN0]服从均匀分布，即第i条裂隙的初始纵横比为：

(8)

(9)

(10)

(11)

另外，由式(8)和式(9)可得：

(12)

(13)

再将式(13)代入式(6)有：

(14)

(15)

如果把σ3=0时岩石弹性模量记为E0，则由式(14)可得：

(16)

也可表示为：

(17)

将式(17)代入式(14)有：

(18)

式(18)即为σ3≤T时，岩石弹性模量E与σ3的关系；当σ3>T时，岩石中裂隙已全部闭合，有E=Es，因此，岩石弹性模量变化的分析模型可表示为：

(19)

式中，Es可由足够大围压下三轴压缩试验曲线线性段斜率获得；E0可由单轴压缩试验曲线线性段斜率确定；T可利用低围压下(岩石中裂隙未全部闭合)三轴压缩试验曲线线性段斜率E与相应围压σ3由基于式(18)的拟合分析方法获得。

式(19)即为岩石弹性模量变化的分析模型，需要说明的是，只要令T=0，式(19)即可表示岩石三轴压缩试验中弹性模量不随围压变化而改变的情况。也即本文模型同时适用于岩石弹性模量变化及保持为常数两种情形，较之前模型有明显改进。

4 岩石统计损伤本构模型

(20)

(21)

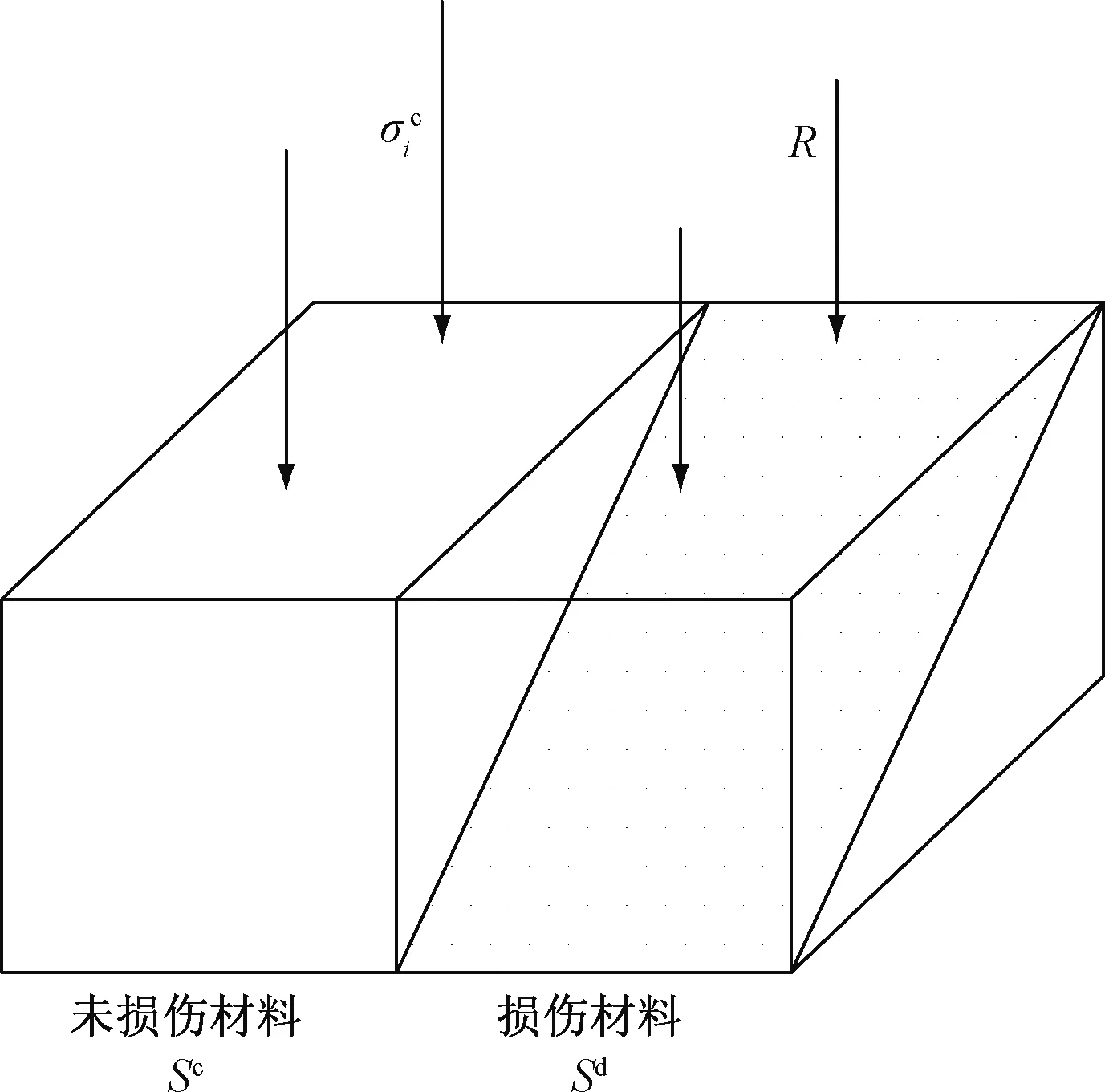
图2 岩石基质受力分析Fig.2 The mechanical analysis for rock

定义损伤变量D为：

(22)

将式(20)和式(22)代入式(21)，可得：

(23)

(24)

(25)

(26)

(27)

式中：εi——岩石的宏观应变。

将式(25)～式(27)代入到式(24)，可得：

(28)

又由式(23)有：

(29)

(30)

将式(29)和式(30)代入到式(28)，可得：

(31)

对于损伤部分应力R，由文献[8,9]，其可表示为：

(32)

式中：cr，φr——岩石残余黏聚力和残余内摩擦角。

将式(31)和式(32)代入式(23)可得：

(33)

可以看出，要建立岩石统计损伤本构模型，还需解决损伤变量D如何确定的问题。为此，引进文献[7～9]的方法，可得：

(34)

式中：m，F0——岩石微元强度F的Weibull分布参数。

F可由Drucker-Prager准则表示为[9,15]：

(35)

(36)

(37)

又可分别表示为[15]：

(38)

(39)

(40)

(41)

(42)

将式(34)代入到式(33)即可得到本文建立的三轴试验条件下的岩石统计损伤本构模型，可表示为：

(43)

(44)

(45)

要模拟岩石变形破坏的全过程，还需解决模型参数m和F0如何确定的问题。为此，引进文献[8,9]的方法，即由岩石应力应变曲线的极值特性有：

(46)

式中，σp和εp分别表示岩石应力应变曲线峰值点处的最大主应力和轴向应变，由文献[3,9]的结论，σp和εp与σ3之间存在如下的经验关系：

(47)

(48)

式中：cp，φp——岩石峰值强度的黏聚力和内摩擦角；b，a——常数，可由式(49)通过线性拟合获得。

于是，将式(43)代入到式(46)，由文献[8]的方法即可获得m和F0的表达形式，可表示为：

(49)

(50)

(51)

(52)

(53)

(54)

至此，已获得本文建立的考虑弹性模量变化的岩石统计损伤本构模型及参数确定方法。

5 实例分析与验证

为验证本文模型的合理性与可行性，引用文献[12]的试验资料进行分析，该试验所用的岩石为红砂岩，根据试验曲线由本文参数确定方法可得岩石的相关力学参数(表1)，由文献[9]的方法即可获得本文模型的理论曲线(图3)。同时，将本文和文献[8]模型的理论曲线与文献[12]试验曲线做对比分析，如图4所示。由此可以看出：

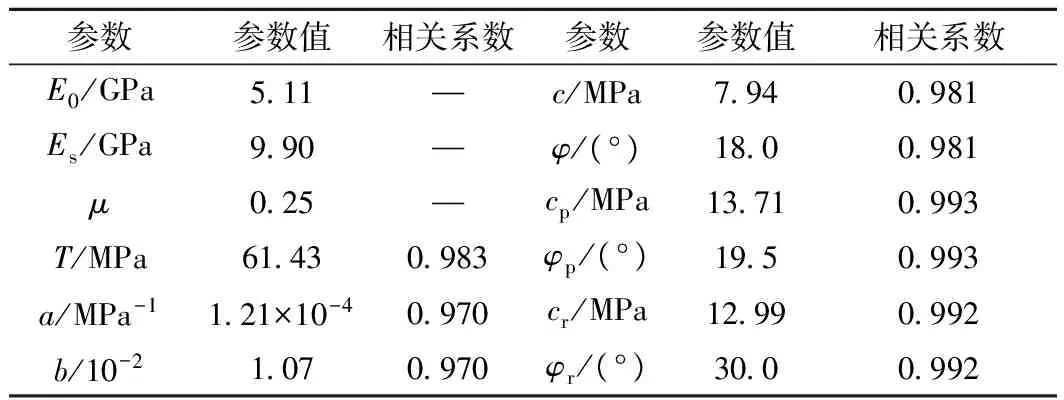
表1 岩石本构模型参数Table 1 Parameters of rock constitutive model

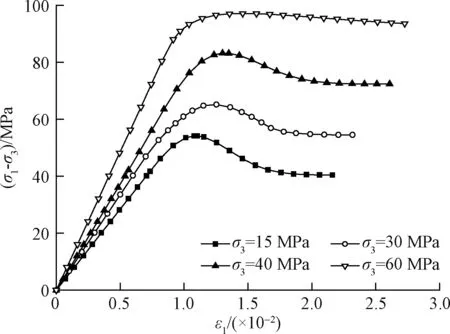
图3 本文模型理论曲线Fig.3 The theoretical curves of the model this paper proposed

图4 试验曲线与理论曲线对比Fig.4 Comparison between theoretical and test curves

(1)本文模型可反映三轴压缩试验中岩石弹性模量随围压变化而改变的特性。

(2)本文模型可反映岩石损伤后变形的应变硬化和软化及残余强度变形特征，具备现有模型的优点。

(3)与文献[8]相比，本文模型曲线更为接近试验曲线，模拟效果更好。

6 结论

(1)通过分析不同类型空隙对岩石变形性质的影响，获得了岩石弹性模量变化仅与岩石中未闭合裂隙数的变化有关的结论，并基于此，建立了岩石弹性模量变化的分析模型，为岩石变形全过程模拟研究打下基础。

(2)引入统计损伤理论，考虑损伤阈值的影响和残余强度变形特征，建立了岩石统计损伤本构模型，并给出基于三轴压缩试验曲线的模型参数确定方法。本文模型不仅可反映岩石弹性模量变化的特性，且可反映岩石应变软硬化和残余强度变形特征。

(3)通过试验曲线、本文和同类模型理论曲线的对比分析，表明了本文模型的合理性与优越性。

[1] 唐春安.岩石破裂过程中的灾变[M].北京：煤炭工业出版社，1993.[TANG C A. Catastrophe in rock unstable failure[M].Beijing: China Coal Industry Publishing House,1993.(in Chinese)]

[2] 曹文贵, 赵衡, 张玲, 等.考虑损伤阀值影响的岩石损伤统计软化本构模型及其参数确定方法[J].岩石力学与工程学报, 2008, 27(6):1148-1154.[CAO W G, ZHAO H, ZHANG L,etal. Damage statistical softening constitutive model for rock considering effect of damage threshold and its parameters determination method[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6):1148-1154. (in Chinese)]

[3] LI X, CAO W G, SU Y H. A statistical damage constitutive model for softening behavior of rocks[J]. Engineering Geology, 2012, 143-144:1-17.

[4] 曹文贵, 莫瑞, 李翔.基于正态分布的岩石软硬化损伤统计本构模型及其参数确定方法探讨[J].岩土工程学报, 2007, 29(5):671-675.[CAO W G, MO R, LI X. Study on statistical constitutive model and determination of parameters of rock based on normal distribution[J].Chinese Journal of Geotechnical Engineering, 2007, 29(5):671-675.(in Chinese)]

[5] CAO W G, ZHAO H, LI X,etal. Statistical damage model with strain softening and hardening for rocks under the influence of voids and volume changes[J]. Canadian Geotechnical Journal,2010,47(8):857-871.

[6] ZHOU G L, THAM L G, LEE P K K,etal. A phenomenological constitutive model for rocks with shear failure mode[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2001, 25(25): 391-414.

[7] 张超, 曹文贵, 王江营. 考虑损伤阈值影响的岩石脆-延性转化统计损伤本构模型研究[J]. 水文地质工程地质, 2013, 40(5):45-50. [ZHANG C, CAO W G, WANG J Y. A study of the statistical damage constitutive model for the brittle-ductile transition of rock with consideration of damage threshold[J]. Hydrogeology & Engineering Geology, 2013, 40(5):45-50. (in Chinese)]

[8] 曹文贵, 赵衡, 李翔, 等.基于残余强度变形阶段特征的岩石变形全过程统计损伤模拟方法[J].土木工程学报, 2012,45(6):139-145. [CAO W G, ZHAO H, LI X,etal. A statistical damage simulation method for rock full deformation process with consideration of the deformation characteristics of residual strength phase[J].China Civil Engineering Journal, 2012, 45(6):139-145.(in Chinese)]

[9] Zhao H, Shi C J, Zhao M H,etal. Statistical Damage Constitutive Model for Rocks Considering Residual Strength[J]. International Journal of Geomechanics, 2016,04016033:1-9.

[10] Bésuelle P, Desrues J, Raynaud S. Experimental characterisation of the localisation phenomenon inside a Vosges sandstone in a triaxial cell[J]. International Journal of Rock Mechanics & Mining Sciences, 2000, 37(8):1223-1237.

[11] 尤明庆. 岩石试样的杨氏模量与围压的关系[J]. 岩石力学与工程学报, 2003, 22(1):53-60. [YOU M Q. Effect of confining pressure on the Young’s Modulus of rock specimen[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1):53-60. (in Chinese)]

[12] 林卓英,吴玉山.岩石在三轴压缩下脆-延性转化的研究[J].岩土力学,1992,13(2,3):45-53. [LIN Z Y,WU Y S.Research on the brittle-ductile transition property of rocks under triaxial compression[J].Rock and Soil Mechanics，1992，13(2,3)：45-53(in Chinese)]

[13] 陈颙, 黄庭芳. 岩石物理学[M]. 北京: 北京大学出版社, 2001. [CHEN Y, HUANG T F. Rock physics[M]. Beijing: Peking University Press, 2001. (in Chinese)]

[14] WALSH J B. The effect of cracks on the compressibility of rock[J]. Journal of Geophysical Research-atmospheres, 1965, 70(2)：381-388.

[15] 曹文贵, 赵衡, 张永杰, 等.考虑体积变化影响的岩石应变软硬化损伤本构模型及其参数确定方法[J].岩土力学, 2011, 32(3):647-654.[CAO W G, ZHAO H, ZHANG Y J,etal. Strain softening and hardening damage constitutive model for rock considering effect of volume change and its parameters determination method[J].Rock and Soil Mechanics, 2011,32(3):647-654. (in Chinese)]

责任编辑：张明霞

A statistical damage constitutive model of rocks consideringthe variation of the elastic modulus

CAO Wengui， YANG Shang， ZHANG Chao

(GeotechnicalEngineeringInstituteofHunanUniversity，Changsha,Hunan410082，China)

In order to establish a more advanced statistical damage constitutive model for rocks, this paper contraposed the deficiency that current models have difficulty in reflecting the characteristics that the elastic modulus would vary with the confining pressures under the conditions of triaxial compression test for some certain rocks, analyzed the mechanism of the rock elastic modulus variation from the perspective of the influences of voids of different kinds on the rock deformation characteristics, and on the basis, a method to research the variation of elastic modulus for rocks has been set up according to the relationship between elastic parameters and the number of cracks which are still unclosed inside the rocks. Afterwards, by introducing the statistical damage theory and taking into account the influences of the damage threshold and the deformation characteristics of the residual strength, a new statistical damage constitutive model which is capable of simulating the complete deformation process of rocks would be built, furthermore, a method to determine the parameters in the model has also been provided based on the triaxial compression test curves of rocks. The model this paper proposed is able to manifest the rock elastic modulus variation with the confining pressure while it possesses the advantages of the existing models and is capable of simulating the rock complete deformation process satisfyingly. Finally, through the comparison analysis among the experimental and theoretical curves of the proposed model and another similar model, the rationality and superiority of the proposed model have been demonstrated.

variation of elastic modulus; damage threshold; residual strength; statistical damage theory; constitutive model

2017-02-19;

2017-03-06

国家自然科学基金项目资助(51378198)；高等学校博士学科点专项科研基金项目资助(20130161110017)

曹文贵(1963-)，男，教授，博士生导师，主要从事岩土工程科研与教学工作。E-mail:cwglyp@21cn.com

10.16030/j.cnki.issn.1000-3665.2017.03.07

TU45

A

1000-3665(2017)03-0042-07