地理加权回归模型在网络诈骗分析中的应用

鄢文凤，孙玲琍

(1.华中农业大学 理学院，武汉 430070；2.华中农业大学 统计研究所，武汉 430070)



地理加权回归模型在网络诈骗分析中的应用

鄢文凤1，孙玲琍2*

(1.华中农业大学 理学院，武汉 430070；2.华中农业大学 统计研究所，武汉 430070)

利用2014年中国网络诈骗研究报告中的数据，针对中国大陆31个省级尺度的地区，结合相关资料，最终选择城镇人口比重、网络普及率、各省GDP、各省人口总数、男性占比作为解释变量，经过探索性空间分析，可得31个省的网络诈骗数量具有空间自相关性，说明网络诈骗数及影响因素适用地理加权回归(GWR)模型. 通过对GWR模型与普通线性回归(OLS)模型的比较，发现GWR模型的AIC，σ2，R2和校正R2均优于OLS模型，这说明GWR模型更能深刻揭示网络诈骗数及其影响因素的空间关系.

网络诈骗;空间自相关性;地理加权回归模型

2016年8月23日，山东省18岁女孩徐玉玉，被诈骗电话骗光学费后，郁结于心，最终心脏骤停离世的新闻引起了人们广泛的关注.8月25日，大二学生小宋，也因连续遭电信诈骗，心脏骤停离世.8月29日，清华大学一老师，被电信诈骗骗走人民币1 760万元.

这些近期频频发生的电信诈骗案件引起了全社会的关注，社会愤恨和声讨声不断，网络媒体也纷纷发声评论，但显然报道只是冰山一角，现实情况比想象的严峻很多.

据中国互联网信息中心(CNNIC)数据显示，截至2014年12月，中国网民规模已达6.49亿人.其中，网络购物用户规模达到3.61亿人，为全球各国网购人群规模之最．在网络交易规模不断扩大的同时，无论是从诈骗金额和诈骗人数来看，网络诈骗已成为网络犯罪中增速最快的犯罪类型，同时也是网络空间中最为严重的社会问题．因此分析网络诈骗的影响因素，建立模型求解各影响因素与网络诈骗的之间关系，对理解网络诈骗的形成原因，预防网络诈骗都会有指导性的作用．

通过查阅相关文献[1-6]，发现研究这类网络诈骗的文章大多以描述网络诈骗特点和预防措施为主，而从统计学的角度分析网络诈骗的影响因素并建立量化指标，这方面的研究几乎为空白. 因此本文通过分析网络诈骗的影响因素，建立多元线性回归，同时又考虑到网络诈骗呈现空间非平稳性，从而引入地理加权回归模型，对网络诈骗的影响因素进行统计学分析，从而揭示出网络诈骗数及其影响因素的空间关系．

1 样本数据

按照行政区划分，中国大陆目前有31个省级(省、直辖市和自治区)尺度的地区，包括北京、天津、上海和重庆4个直辖市，5个自治区(内蒙古、西藏、广西、宁夏、新疆)以及22个省．

被解释变量:网络诈骗数据，来源于2014年中国网络诈骗研究报告，来源网址：http://mt.sohu.com/20160225/n438446190.shtml．

选取解释变量：根据2014年中国网络诈骗研究报告，男性受害者占63.7%，女性占36.3%，男性受害者占比大大高于女性，因此选取自变量时须将各省男性占比考虑进去．进行相关性分析，发现网络诈骗数与城镇人口比重、网络普及率、各省GDP、各省人口总数呈现比较强的线性相关关系，因此也把这些变量作为影响因素．男性占比、各省城镇人口比重、人均可支配收入、各省GDP数据均来源于2014年中国统计年鉴，而网络普及率数据来源于http://www.chinabgao.com/stat/stats/40545.html．

2 地理加权回归模型

在普通线性回归方程中，对于n组数据利用普通线性回归最终得到一组回归系数．而当系数在不同地理位置上表现不同时，也就是系数随着地理位置变化时，如果仍然采用上面方法，得到的是掩盖了地理位置后的系数的平均值，与实际情况不相符合，同时模型也会不准确．针对这一问题，Fotheringham等在前人研究的基础上，提出了地理加权回归模型(Geographically Weighted Regression Model-GWR)．

地理加权回归模型可以表示为以下形式：

(1)

式(1)中，yi表示区域i处的因变量，xik表示第k个自变量在区域i处的取值，εi为残差，且εi～N(0,σ2)；cov(εi,εj)≠0(i≠j);(ui,vi)为区域i处的位置函数(如区域中心的经纬度坐标)，βik为区域i处的第k个回归参数．

由于地理加权回归模型中的回归参数在每个区域上都是不同的，则上述模型中待估参数个数为n(p+1)，远远大于观测数据n，此时如果仍然用传统最小二乘将得不到理想的结果，同时地理信息也未被考虑进去，一些非参数方法很好的解决了这类问题．Brunsdon等人[7-10]提出了局部加权最小二乘：在计算区域i的回归参数时，利用其邻域上的观测值建立局部回归．在估算区域i的回归参数时，不同观测值重要性不同，距离越近的观测值的重要性越大，反之越小．根据加权最小二乘回归，求i点的回归系数：

(2)

通过使上式达到最小来估计．其中wij为权重，是回归点i与其他区域j之间地理距离dij的减函数．

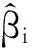
(3)

2.1 空间权函数的选择

wij=e(-(dij/b))2

(4)

其中，b称为带宽，用来描述权重与距离之间函数关系的非负衰减函数．

2.2 空间权函数带宽的优化

从式(4)中可以看到，权重wij随着距离dij的增大而减小，且带宽越小衰减速度越快．常用的优化带宽[12]的方法有：交叉验证，AIC准则和BIC准则．本文采用交叉验证求解带宽，该方法的表达为：

3 建立模型

3.1 全局空间自相关分析(Global moran's I)

全局空间自相关分析(GlobalMoran'sI)[13]，通过计算全局空间自相关统计量来判断总体网络诈骗数量在空间上是否具有相关性．Global Moran's I统计量是常用的全局空间自相关度量指标，给定置信水平时，若Moran's I显著且正，则表示网络诈骗频发的区域在空间上集聚，或表示网络诈骗数量较少的区域在空间上集聚．值越趋近于1，网络诈骗总体空间差异越小．反之，若Moran's I显著且负，则表明区域与其周边地区的网络诈骗数量具有显著的差异．值越趋近于-1，区域地价的网络诈骗数量差异越大．当且仅当Moran's I的显著性检验通过，观测值之间才能认为相互独立，此时才能用传统的方法计算，如图1所示．

可以看出，网络诈骗数量多的地方大多聚集在东南部地区，在空间上呈现一定程度的聚集性．计算全局Global Moran's I=0.25，Z-score=2.61，P=0.012(<0.05)，可以证明31个省的网络诈骗数据具有全局的空间自相关性．

3.2 OLS建模

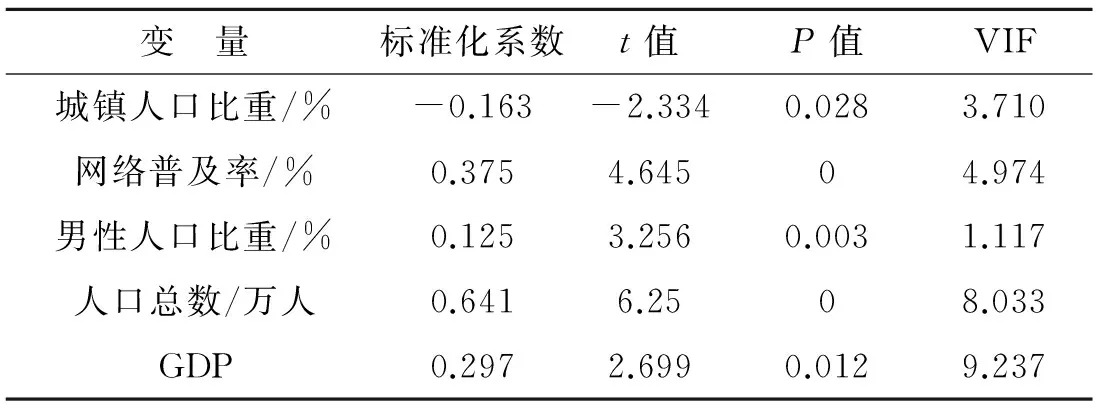
表1 OLS建模参数估计结果

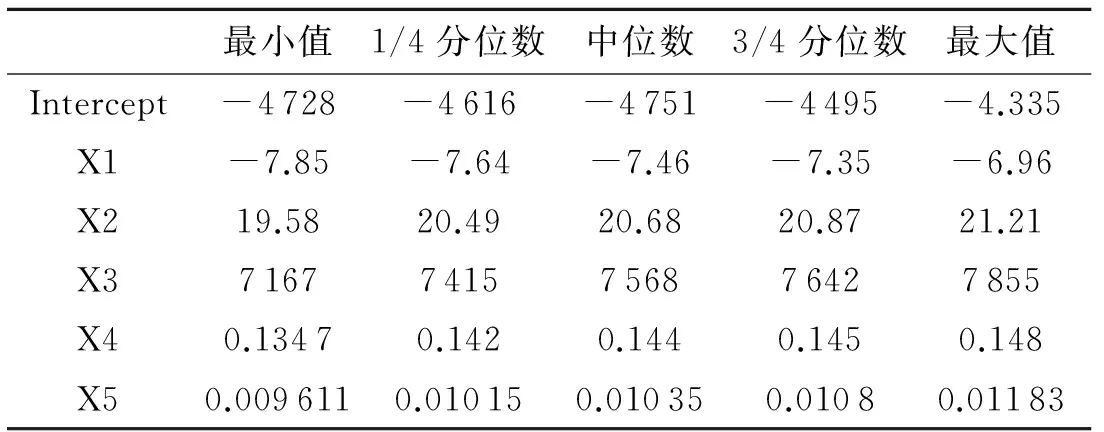
表2 系数的四分位值

表3 模型主要指标的比较

在实际中，为初步了解变量间的相互关系，首先进行OLS建模[14]，得到显著性检验的F=147.672，P=0，说明这5个解释变量与网络诈骗数具有的相关关系，参数估计结果见表1．

这5个自变量的P值均小于0.05，通过显著性检验．同时共线性诊断中VIF高达9.237，说明共线性比较严重，综合之前的探索性分析，因此有必要进行GWR建模．

3.3 GWR模型

对网络诈骗数据使用GWR建模，因此选择了应用最广泛的Gauss核函数法，使用交叉验证确定最优带宽为b=26.7．最终可以根据各省之间距离确定权重矩阵，得到影响网络诈骗的因素在每个样本点上对应的取值，下面将该取值的四分位数值列出来，如表2所示．残差平方和为362 885，决定系数变化的范围的[0.966,0.971]．

4 模型对比

表3比较了相同自变量和因变量形式的地理加权回归模型和普通线性回归模型，分别比较了他们的R2，残差平方和SSE，模型的标准差，以及AIC．

比较两种模型的评价指标发现，GWR模型的AIC,R2,SSE,σ全面优于OLS．根据Fotheringham[15-16]等提出的GWR模型评价标准：若GWR模型与OLS的AIC之差大于3，则表明即使把GWR模型的复杂度考虑在内，其模型拟合效果也比OLS好．本研究中的GWR模型的AIC值为399.43，远小于OLS模型的AIC值405.14，证明了GWR模型在处理这一类具有空间自相关性问题的优越性，同时也证明了GWR模型在网络诈骗上的应用具有实际意义．

[1] 程娟，万建平.空间统计在公共卫生事业中的应用[J].统计与决策,2009(13):153-154.

[2] 郝文江.网络诈骗案件分析与防范对策[J].吉林公安高等专科学校学报,2008,23(2):103-107.

[3] 刘守芬，孙晓芳.论网络犯罪[J].北京大学学报(哲学社会科学版),2001,38(3):114-122.

[4] 王松丽.网络诈骗犯罪的实证分析与对策研究:以安徽省为例[J].学术界,2009(6):198-204.

[5] 郭春涛.网络诈骗的概念、主要表现及犯罪构成研究[J].信息网络安全,2011(4):61-63.

[6] 于志刚.网络犯罪与中国刑法应对[J].中国社会科学,2010(3):109-126,222.

[7] BRUNSDON C,AITKIN M,FOTHERINGHAM S,et al.A comparison of random coefficient modelling and geographically weighted regression for spatially non-stationary regression problems[J].Geographical & Environmental Modelling,1999,3(1):47-62.

[8] BRUNSDON C,FOTHERINGHAM A S,CHARLTON M E.Geographically Weighted Regression:A Method for Exploring Spatial Nonstationarity[J].Geographical Analysis,1996,28(4):281-298.

[9] BRUNSDON C,FOTHERINGHAM S,CHARLTON M,et al.Geographically Weighted Regression as a Statistical Model[J].Encyclopedia of Gis,2001,47(3):431-443.

[10] BRUNSDON C,FOTHERINGHAM A S,CHARLTON M.Geographically weighted summary statistics- a framework for localised exploratory data analysis[J].Computers Environment & Urban Systems,2002,26(6):501-524.

[11] 覃文忠.地理加权回归基本理论与应用研究[D].上海：同济大学，2007.

[12] 肖雄，杨长虹，谭柯，等.地理加权回归模型在传染病空间分析中的应用[J].中国卫生统计,2013(6):833-836，841.

[13] 叶阿忠，吴继贵，陈生明，等.空间计量经济学[M].厦门：厦门大学出版社，2015.

[14] 何晓群,刘文卿.应用回归分析[M].4版.北京：中国人民大学出版社，2015.

[15] FOTHERINGHAM A S,CHARLTON M E,BRUNSDON C.Geographically Weighted Regression:A Natural Evolution of the Expansion Method for Spatial Data Analysis[J].Environment & Planning A,1998,30(11):1905-1927.

[16] AKAIKE H.A New Look at the Statistical Model Identification[J].IEEE Trans Automat contr,1974,19(6):716-723.

责任编辑：高 山

Application of Geographical Weighted Regression Model in Analyzing Internet Fraud

YAN Wenfeng1, SUN Lingli2*

(1.College of Science, Huazhong Agricultural University, Wuhan 430070,China；2.Institute of Statistics, Huazhong Agricultural University, Wuhan 430070, China)

By using the data of Internet fraud research report of China in 2014,collecting and collating the national 31 provincial scale regions,and combining with relevant information,we finally select the proportion of urban population,network penetration rates,GDP of all provinces,the total population for each province,and the proportion of men as explanatory variables.After exploring the spatial variation of the number of Internet fraud and its influencing factors,we have found that the numbers of Internet fraud for 31 provinces have a spatial autocorrelation,which shows that geographical weighted regression model can be applicable.By comparing GWR model with ordinary linear regression model,we find that GWR model is superior to OLR model and GWR model can deeply reveal the spatial relationship between the numbers of Internet fraud and the influencing factors.

internet fraud;spatial autocorrelation;geographic weighted regression

2017-01-04.

华中农业大学研究生课程建设项目(2015KJ 26);华中农业大学创新创业类通识课程建设项目(201606);中央高校基本科研业务费专项基金项目(2662016QD006).

鄢文凤(1993-)，女，硕士生，主要从事空间统计的应用研究；*

孙玲琍(1978-)，女，博士，副教授，主要从事应用统计的研究.

1008-8423(2017)02-0148-04

10.13501/j.cnki.42-1569/n.2017.06.008

O212.1

A