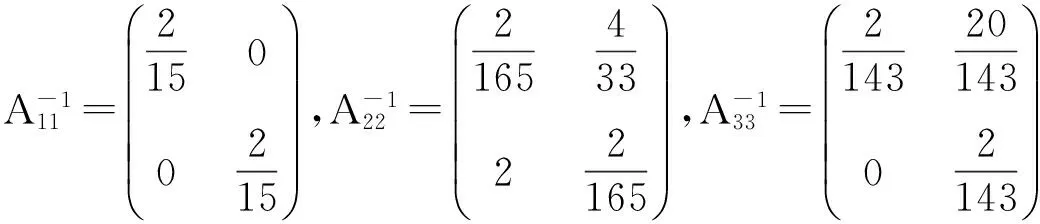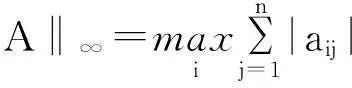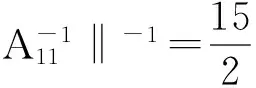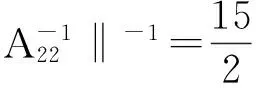块α-对角占优矩阵的充要条件
2017-06-21高会双韩贵春
高会双,韩贵春
(内蒙古民族大学 数学学院, 内蒙古 通辽 028000)
块α-对角占优矩阵的充要条件
高会双,韩贵春
(内蒙古民族大学 数学学院, 内蒙古 通辽 028000)
介绍了块α-对角占优矩阵的概念,给出了两个块α-对角占优矩阵的充要条件,进而得到了块H-矩阵新的判定准则,并用数值例子说明了这些结论的有效性.
块对角占优矩阵;块α-对角占优矩阵;块H-矩阵
1 预备知识
为了适应大规模矩阵计算的需要,矩阵的分块技术越来越引起大家的关注.20世纪60年代,Feingold和Varga引入了块对角占优矩阵的概念[1].块对角矩阵在求解线性方程组等方面起着重要作用.近年来,块对角优矩阵在许多文献中进行了深入讨论[2-9].本文给出了两个判定块-对角占优矩阵的充要条件,进而得到了块H-矩阵新的判定准则,拓展了块H-矩阵的判定条件,最后用数值例子说明了这些结论的有效性.
设A=(aij)∈Cn×n为n阶复方阵,分块如下:
(1)
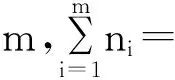

M1={i∈M|Pi(A)<‖Aii-1‖-1 M3={i∈M|‖Aii-1‖-1≥Ri(A)>Pi(A)};M4={i∈M|‖Aii-1‖-1≥Pi(A)>Ri(A)}; M5={i∈M|‖Aii-1‖-1>Pi(A)=Ri(A)};M6={i∈M|‖Aii-1‖-1≤Ri(A),‖Aii-1‖-1≤Pi(A)}. 显然有M=M1∪M2∪M3∪M4∪M5∪M6. 若对任意i∈M都有‖Aii-1‖-1≥(>)Pi(A),则称A为块(严格)对角占优矩阵, 记为A∈BD0(A∈BD);若存在正对角阵X(矩阵X的分块形式与矩阵A的分块形式相同), 使得AX∈BD,则称A为块H矩阵(或块广义严格对角占优矩阵), 记为A∈BH. 定义1 设A=(aij)∈Cn×n, 分块如式(1), 若存在α∈[0,1], 使得: (‖Aii-1‖)-1≥(>)αPi(A)+(1-α)Ri(A),∀i∈M, (2) 则称A为块(严格)α1-对角占优矩阵, 记为A∈BD1(α0)(A∈BD1(α)). 定义2 设A=(αij)∈Cn×n, 分块如式(1), 若存在α∈[0,1], 使得: ‖Aii-1‖-1≥(>)Pi(A)αRi(A)1-α,∀i∈M, (3) 则称A为块(严格)α2-对角占优矩阵, 记为A∈BD2(α0)(A∈BD2(α)). 引理1[7]设A=(αij)∈Cn×n,分块如式(1), 若存在α∈[0,1], 使得: ‖Aii-1‖-1≥(>)Pi(A)αRi(A)1-α,∀i∈M,则A为块H-矩阵. 首先给出了两个判定块α1-对角占优矩阵的充要条件,进而得到块H-矩阵新的判定准则. 定理1 设A=(αij)∈Cn×n, 分块如式(1), 则A∈BD1(α)的充分必要条件是M6=φ, 且对任意的i∈M1,j∈M2, 有: (4) 证明 充分性.由指标集M1和M2的取法可知, 对任意的i∈M1,j∈M2, 有: Pi(A)<‖Aii-1‖-1 则: 则由式(4)式知存在α∈(0,1), 使得: (5) 由式(5)中第一个不等式知,对任意的i∈M1, 有:(‖Aii-1‖)-1>αPi(A)+(1-α)Ri(A). 同理, 由式(5)中第二个不等式知,知对任意的j∈M2, 有:(‖Ajj-1‖)-1>αPj(A)+(1-α)Rj(A). 对任意的i∈M3∪M4∪M5及任意的α∈(0,1), 显然有:(‖Aii-1‖)-1>αPi(A)+(1-α)Ri(A). 综上所述, 由条件知M6=φ,对任意i∈M1∪M2∪M3∪M4∪M5∪M6存在α∈(0,1), 使得: (‖Aii-1‖)-1>αPi(A)+(1-α)Ri(A). 即A∈BD1(α). 必要性:因为A∈BD1(α), 显然有M6=φ,且对任意的i∈M1,(‖Aii-1‖)-1>αPi(A)+(1-α)Ri(A), 即: (6) 对任意的j∈M2, 有(‖Ajj-1‖)-1>αPj(A)+(1-α)Rj(A),即: (7) 仿照定理1的证明,可以得到下面结论. 定理3 设A=(αij)∈Cn×n,分块如式(1), 且M6=φ,若对任意的i∈M1,j∈M2, 有: 证明 由定理1和定理2可知,A∈BD1(α).再由Holder不等式,则存在α∈(0,1)对任意的i∈M1,(‖Aii-1‖)-1>αPi(A)+(1-α)Ri(A)≥Pi(A)αRi(A)1-α.由引理1可知,A为块H-矩阵. 例1 由本文记号有P1(A)=6,P2(A)=6,P3(A)=7;R1(A)=6,R2(A)=8,R3(A)=5.显然有:{M1}={2},{M2}={3},{M5}={1},M3=M4=M6=φ. 即满足定理3 的条件, 所以矩阵A为非奇异块H-矩阵. [1] DAVID G FEINGOLD,RICHARD S VARGA.Block diagonally dominant matrices and generalizations of the Gerschgorin Circle Theorem[J].Pacific J Math,1962,12:1241-1250. [2] L YU KOLOTILINA.Nonsingularity/singularity criteria for nonstrictly block diagonally dominant matrices[J].Linear Algebra Appl,2003,359:133-159. [3] ZHANG C Y,LI Y T,CHEN F.On Schur complement of block diagonally dominant matrices[J].Linear Algebra Appl,2006,414:533-546. [4] 杨鹏,冉瑞生,黄廷祝.奇块H-矩阵的充分条件[J].电子科技大学学报,2004,33(2):204-207. [5] 刘建州,徐映红,廖安平. 义块对角占优矩阵的判定[J].高等学校计算数学学报,2005,27(3): 250-257. [6] 肖丽霞.非奇异H-矩阵的含参数α的迭代判定法[J].内蒙古民族大学学报(自然科学版),2015,30(2):96-98. [7] 高中喜,黄廷祝,刘福体. 块H-矩阵的简捷判定[J].工程数学学报,2004,21(3): 340-344. [8] 李庆春,刘磊. 矩阵对角占优性的推广[J].吉林师范学院学报,1996,17(5):4-7. [9] 高会双,韩贵春,肖丽霞. 块对角占优矩阵的讨论[J].纯粹数学与应用数学,2014,30(1):53-59. 责任编辑:高 山 Sufficient and Necessary Conditions for Block α - diagonally Dominant Matrices GAO Huishuang,HAN Guichun (College of Mathematics,Inner Mongolia University for nationalities,Tongliao 028000,China) In this paper, the concept of block α-diagonally dominant is introduced and two sufficient and necessary conditions for block α-diagonally dominant matrices are given.A new practical criterion for blockH-matrices is obtained.Finally,the effectiveness of the results is illustrated by numerical examples. block diagonally dominant matrices;block α-diagonally dominant matrices;blockH- matrices 2017-03-13. 内蒙古自治区自然科学基金项目(2016MS0118);内蒙古民族大学科学研究基金项目(NMDYB15089);内蒙古民族大学科学研究基金项目(NMDYB1778). 高会双(1980-), 女,副教授,主要从事算子代数和数值代数的研究. 1008-8423(2017)02-0131-03 10.13501/j.cnki.42-1569/n.2017.06.003 O151.21 A2 主要结果
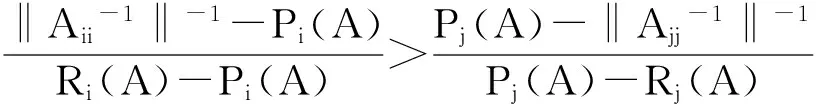
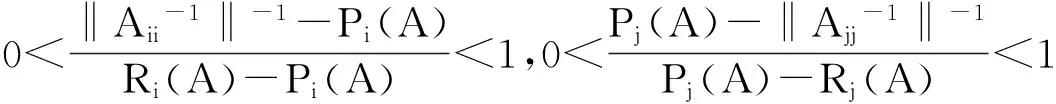

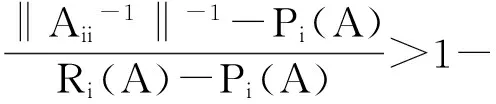

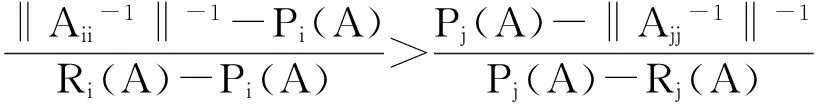

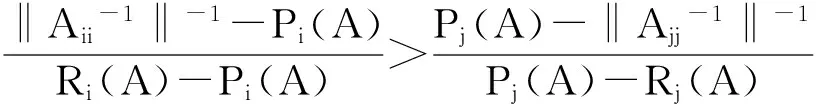
3 数值算例