融合多种搜索策略的差分进化大规模优化算法*

罗家祥 倪晓晔 胡跃明

(华南理工大学 自动化科学与工程学院， 广东 广州 510640)

融合多种搜索策略的差分进化大规模优化算法*

罗家祥 倪晓晔 胡跃明

(华南理工大学 自动化科学与工程学院， 广东 广州 510640)

多峰、高维的大规模优化问题是当前优化领域的研究热点.文中以协同进化算法为框架，提出了一种融合多种搜索策略的差分进化大规模优化算法.基于分解的思想，该算法首先利用自适应差分进化算子对子问题进行局部优化求解;然后引入基于模拟退火的随机搜索机制提高算法的全局搜索能力，并结合局部搜索链对解空间进行深度搜索.采用大规模优化标准函数对算法进行测试，结果表明，文中所提出的算法相比现有算法在平均值和最优解上均取得了更好的优化结果．

大规模优化；协同进化算法；模拟退火；差分进化；局部搜索

在科学研究和工业过程中，大规模优化问题(未知变量多、目标函数结构异常复杂、约束条件数量也十分庞大的优化问题)越来越普遍.该问题具有维度高、变量关系复杂等特点，传统的直接优化方法难以求解[1].智能算法由于计算简便、表现稳定而更多地被应用于求解大规模优化问题[2- 4].但随着问题维度的增加，解空间指数级增加，传统智能算法也难以进行有效求解.近年来，基于分解思想的协同进化对上述问题的求解表现出更好的性能，受到越来越多学者的重视[5- 7].协同进化求解大规模优化问题的思路是:将高维度问题分解为多个子问题，用进化算法对每个子问题求解，再融合子问题的解得到原问题的解[5].

显然，在基于协同进化的大规模优化算法中，子问题求解方法对算法整体性能有着重要影响.多种启发式算法如粒子群(PSO)[7]、差分进化(DE)[8]、人工蜂群(ABC)[9]等算法，被应用到协同进化框架下求解大规模问题.其中，DE算法控制参数少、收敛快且稳定，在该问题上具有更好的求解效果[10].但已有研究表明上述智能方法在求解复杂多峰大规模优化问题时依旧容易陷入局部最优[7- 10].因此如何提高算法的全局搜索能力是大规模优化算法研究值得关注的问题．

为了提高协同进化算法在大规模优化问题上的全局搜索能力，笔者在协同进化算法框架下，采用自适应DE算法求解子问题，并融合基于随机搜索的模拟退火(SA)机制来提高算法跳出局部最优解的能力;同时，引入基于概率的局部搜索链，提高算法的集中搜索能力.为验证算法有效性，使用文献[6]和CEC’2010提出的测试函数[11]进行实验，将仿真结果和现有文献算法进行了对比．

1 大规模优化问题

文中主要考虑求解如下大规模非线性优化问题[12]:

minf(x)

(1)

s.t.x∈Ω⊆RD.

其中，x表示变量，f是定义在RD(R为实数集合，D为变量维数)上的实值函数，称函数f为问题的目标函数，集合Ω为问题的可行域．

大规模优化问题具有维度高、各组成部分之间关系复杂等特点.而许多实际优化问题的目标函数都是非线性、非凸、不可导的，存在多个局部最优解，特别是随着优化问题规模的增大，局部最优解的数目将会迅速增加，有效地求出一般非凸目标函数的全局最优解至今仍是个难题．

2 多搜索策略的差分进化大规模优化算法

2.1 算法流程

文中从全局搜索和局部搜索两方面入手，提出融合模拟退火搜索机制和局部搜索链的协同差分进化方法求解大规模优化问题.DE算法模型简单，求解大规模问题时显示出了较好性能[13]，但其基于精英保留策略的选择机制，在求解多峰复杂大规模优化问题时，依旧容易陷入局部最优.而SA算法概率性接受当前非优解[14]，可在一定程度上弥补DE算法的不足，提高算法全局搜索能力.局部搜索链可进一步提高算法集中搜索能力[15].基于以上考虑，文中提出的算法(简称CoDE-RSA-LSC)以协同进化算法为框架，每个子问题采用DE算法求解，再利用SA机制对解进行随机搜索，最后以基于概率的局部搜索链进一步改进当前解集.设种群X={x1，x2…，xi，…，xN}，N为种群规模;个体xi={xi，1，xi，2，…，xi，D}.算法具体流程如图1所示．

2.2 基于随机种群的分组策略

分组策略将高维大规模优化问题转化为多个低维的子问题，它决定了单个子问题内变量的相关性，影响算法搜索效率.传统策略是将原问题分解为多个单维子问题或者两个子问题[5]，简单但效率低下.随机分解方法[6]固定子问题的维度，每次迭代随机对变量重新分组，该策略已被证明在经过多次迭代后，可将相关变量以较大概率放置到同一个子问题中[8- 9]，从而提高算法的搜索效率．

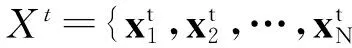
图1 文中算法流程图

2.3 基于自适应差分进化的子问题求解

DE算法通过权重系数F将两个父代个体的差异引入到另一父代个体中产生中间解，再通过交叉和选择算子产生子代.DE算法在求解一般优化问题上显示出了很好的特性[8，10]，因此，也被改进用于求解大规模优化问题，如基于邻域搜索的Nsde算法[10]和自适应的Sade算法[16]等.DE算法的性能很大程度上依赖于变异策略的选择和参数的设置(种群规模N、权重参数F和交叉概率CR)[13]，在算法中自适应调整参数的DE算法表现出了更好的性能[16- 18].基于上述考虑文中采用了基于邻域搜索的自适应差分进化算法(Sansde)[18]来对子问题进行寻优.Sansde算法通过对参数的自适应控制，提高算法的搜索效率.该算法的特点如下:

1) 通过控制参数pm的大小，概率选择DE/rand/1或DE/target- to- best(如式(2)所示)中表现更优的变异算子对当前个体实施变异：

(2)

式中，vi表示变异后的个体，Ui(0，1)表示高斯随机数．

2) 通过控制参数pf的大小，概率选择表现更优的高斯分布或柯西分布随机产生权重系数F．

3) 通过控制参数pCR的大小设定交叉概率CR，使CR自适应地为不同问题和进化不同阶段选择合适的值.

在Sansde算法中，参数pm、pf和pCR的大小根据成功的子代个体数进行自适应调整，从而改变不同策略的选择概率，详见文献[18].需注意的是，在第j个子群进化过程中对个体评估适应值时，个体的其他维度采用整个种群中最好个体的变量值进行计算．

2.4 基于模拟退火的随机搜索机制

SA算法利用优化求解和物理系统退火的相似性，逐步降低非优解的接受概率，缩小算法搜索范围[14，19].研究表明，融合SA的智能算法表现出了更好的搜索特性[20- 22].为了提高DE算法在大规模多峰复杂问题上的求解能力，提出在各子问题求解后，引入基于SA的随机搜索策略RSA．

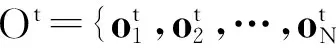
在当前种群中随机选取g个个体{o[1]，o[2]，…，o[g]}进行退火操作.退火过程:

初始化(初始温度T0)，令k=0;

重复 对i=1到Imax

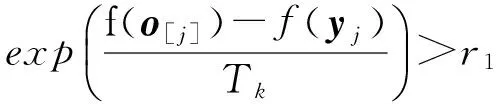
数r1～[0，1])，令o[j]=yj; 更新xbest;

i=i+1;

降温Tk+1=aTk，k=k+1;

若k>Kmax，算法结束．

上述算法中，个体o[j]的每个变量值在不同方向随机值扰动产生yj，增大搜索范围.即对于维度d:

yjd=o[j]d+r2(ud-ld)/10

(3)

其中,r2为-1～1区间的随机数，ud和ld为维度d的上限和下限．

2.5 局部搜索链

局部搜索链[15，23- 24]将前一次局部搜索的结果作为下一次局部搜索的初始点，形成一个搜索链，可进一步挖掘局部搜索的潜能[24].局部搜索是形成局部搜索链的基础，解决大规模问题的常用局部搜索有:①SW算法，该算法是一种自适应步长的随机爬山策略，适应性强，运算成本高; ②MTS算法，该算法对个体的单个或部分变量进行固定值扰动，运算速度快，但适应性不强.SSW局部搜索[15]结合了SW和MTS的思想，对随机选择的部分变量进行自适应步长扰动，具有更好的搜索性能.但对于高维的大规模优化问题，若在每次迭代过程中都对种群进行局部搜索链的搜索，运算成本高，效率低.因此，提出通过概率PL选择是否对当前种群实施SSW搜索链，在利用搜索链的同时，兼顾搜索效率.每次实施局部搜索链的迭代次数为Istr．

3 实验分析

为验证算法的有效性，采用了文献[6]的13个常用测试函数和文献[11]提出的 20个测试函数进行实验.这些函数包含单峰和多峰情况，变量维数可自行设定;同时，根据变量相关性可分为:完全可分解、部分可分解以及完全不可分解3种类型.选择问题规模参数为:D=1 000．

3.1 参数设置

根据文献[6，11]推荐，设定N=100，最大评估次数Es=3×106，d=50;根据文献[18]推荐，设定DE参数的初始值：pm=0.5，pf=0.5，pCR=0.5;根据文献[19]设定基于模拟退火的随机搜索策略(RSA)的参数:降温速度a=0.9，固定温度下随机扰动次数Imax=500.局部搜索链的迭代次数Istr根据文献[24]推荐设定为500，实施概率PL设置为3个水平{0.25，0.50，0.75}进行预实验，根据最佳效果选定PL=0.25.RSA算法参数g、Kmax、T0通过正交试验[25]的方法设定. RSA算法中，退温操作个体数g、降温次数Kmax、温度初始值T0分别选取3个水平，如表1所示．

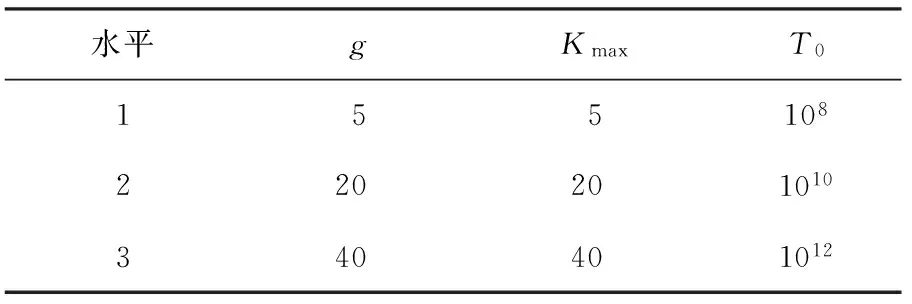
表1 RSA参数水平设置

选择L9(34)作为实验的正交列表，用文献[6]的13个测试函数进行测试，独立运行每种正交水平组合下的算法25次.对第i个测试函数，采用如下指标评价水平组合的优劣:

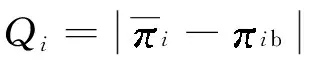
记录每个测试函数对应不同参数水平的Qi值，统计每个参数水平对应最小Qi值时的测试函数个数，选择个数最多的水平作为最佳参数水平.表2列出了对于13个测试函数中的函数F4算法在不同参数水平下的Qi值，说明对于该函数，算法在参数g、Kmax、T0水平为2、3、3组合时表现更好.表3列出了不同水平所对应的函数个数，说明参数g、Kmax、T0在水平为2、2、1组合时，算法对于多数测试函数取得了更好的结果，此时参数对应为:g=20、Kmax=20、T0=108．

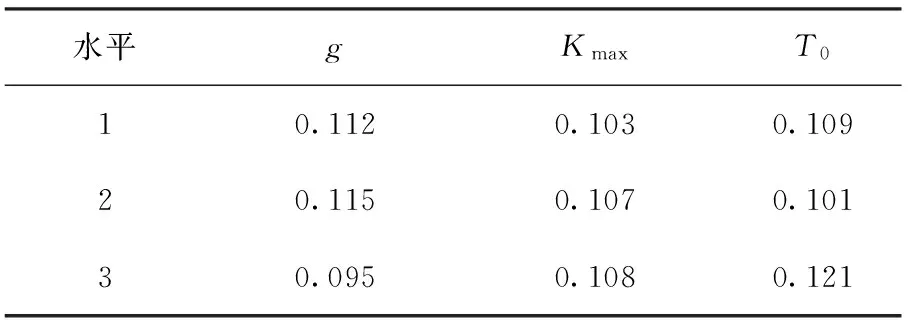
表2 F4的参数水平性能

表3 参数水平对应的函数个数

3.2 算法组成部分重要性分析

自适应DE算法的子问题求解方法、基于SA的RSA、局部搜索链(LSC)是所提出算法CoDE-RSA-LSC的主要组成部分.为了分析RSA和LSC的作用，将两者分别从原算法中去除，采用文献[6]的13个测试函数，将3个算法对每种测试函数运行25次，记录最好解，结果见表4.从表4可得，无论去掉RSA或LSC都将引起算法结果不同程度恶化，CoDE-RSA-LSC取得了最好优化效果.RSA在全局搜索方面作用显著，帮助函数跳出局部早熟收敛;LSC侧重局部集中搜索，可有效提高解的精度.实验结果表明了融合多搜索策略对算法改进的有效性．

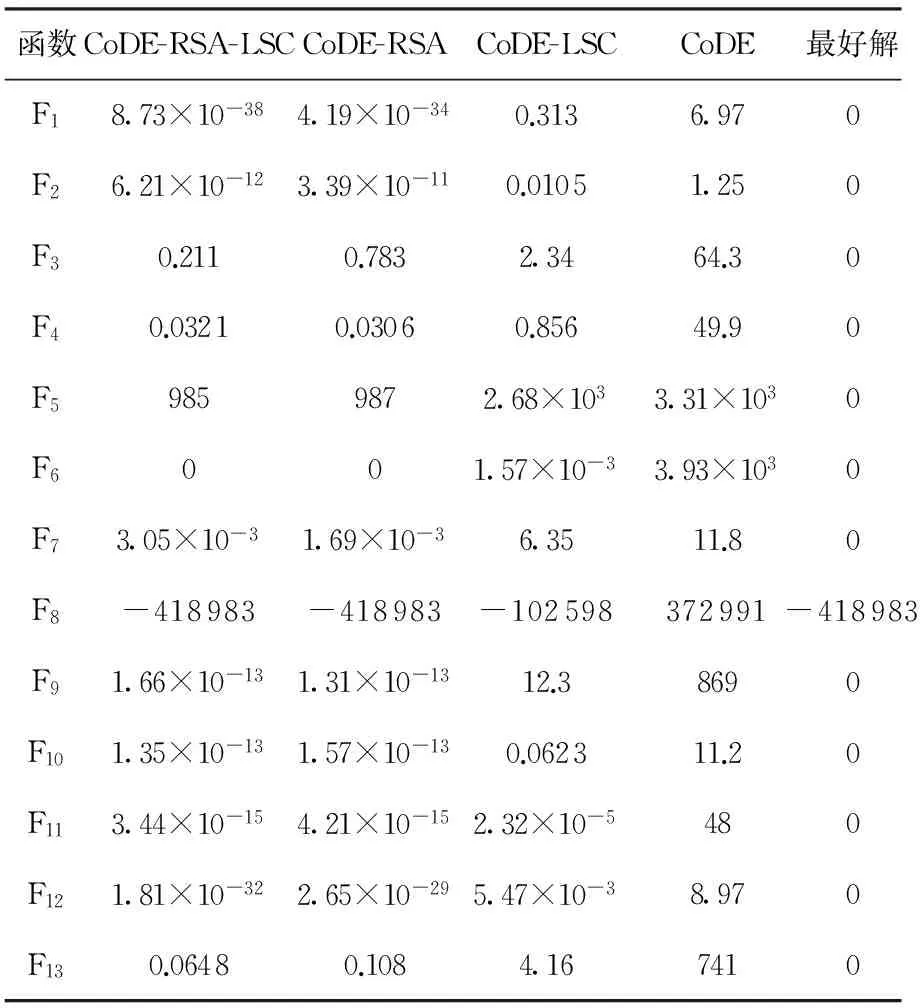
表4 算法组成部分作用比较

3.3 CoDE-RSA-LSC与其他算法的比较分析

本节讨论算法针对文献[11]中20个测试函数的优化结果，与DECC-G[6]、MLCC[17]这两种解决大规模问题常用的效果较好的协同进化算法进行比较.表5给出了测试函数在相同实验条件下分别在CoDE-RSA-LSC、DECC-G和MLCC下独立运算25次的平均结果(最好解，平均值).测试函数已知最优值均为0，设定当算法结果达到10-6时，认为算法得到了函数的最优值,结果见表5．

由表5可得:CoDE-RSA-LSC得到了大部分测试函数的最好解，且平均值皆优于其他算法.对于函数F1、F2、F3，文中算法在最好解,平均值上均取得最好效果， 达到最佳值且表现稳定.对函数F7、F12，最好解、平均值也相应减小， 算法稳定.对于部分可分解函数F17，CoDE-RSA-LSC虽没有逼近最佳值，但是相比MLCC和DECC算法，最好解和平均值均有102数量级的改进.对不可分解函数F19、F20，搜索结果有显著改进:最好解大幅降低逼近最佳值，且在实验终止时最优解仍有下降趋势，表明文中算法有进一步优化的潜力．

表5 CoDE-RSA-LSC与DECC、MLCC算法实验结果比较

以上分析结果表明，CoDE-RSA-LSC算法结合SA全局搜索的特点，可以有效克服DE算法本身的局限性，帮助一些多峰复杂函数跳出局部收敛.同时局部搜索链提高了算法搜索精度，对于大部分大规模问题的求解都有改进效果.文中考虑到算法的时间成本，固定了搜索次数，部分函数在达到最大运算次数后仍有优化的空间．

3.4 算法收敛情况分析

为分析CoDE-RSA-LSC算法自身的收敛性和寻优效果，将算法优化文献[11]中20个测试函数时最好解随着迭代次数增加而变化的过程绘制为收敛曲线，并挑选几个具有代表性的测试函数进行比较，如图2所示．

1) 从测试函数中变量相关性来看:对于可分解函数，算法能够较快收敛，完全达到最优值.对于部分可分解函数，算法曲线呈现两种趋势:曲线朝最优值持续收敛至算法终止时仍有下降趋势;曲线快速下降于某一最好解(部分函数可达到最优值临近解)后趋于稳定.对于不可分解函数，算法不断在达到一个稳定值后跳出局部最优，继续趋进最优解.分析可得，随着测试函数中变量关联性的增加，算法优化结果没有明显的衰减，鲁棒性较好．

2) 从测试函数峰值复杂度来看:对于单峰函数，算法收敛曲线呈单调下降的趋势，或快速达到最优值，或持续向最优值趋进.对于多峰函数，算法曲线存在多个拐点，不断跳出函数的局部最优值，趋近全局优化解.表明文中算法对于不同复杂度的测试函数都有很好的适应性，能有效增强全局搜索能力．

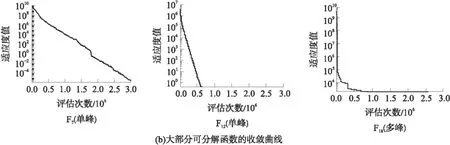
图2 测试函数的最好解收敛曲线

4 结语

文中对协同进化算法解决大规模优化问题的方法进行了研究，提出一种融合多种搜索策略的差分进化大规模优化算法(CoDE-RSA-LSC).算法利用自适应DE算子对子问题进行局部优化;引入基于SA的随机搜索机制提高算法全局搜索能力;并结合局部搜索链对大规模问题进行深度搜索.对文中提出算法与DECC、MLCC算法实验结果进行比较发现，CoDE-RSA-LSC求解大规模问题时取得了更有竞争力的优化效果.进一步算法收敛性分析发现，随着测试函数中变量关联性的增加，算法优化效果没有明显衰减.在面对复杂多峰问题时，算法也表现出了很强的适应性.实验结果表明了文中算法在解决复杂多峰大规模优化问题时的有效性和稳定性．

[1] 肖运海.求解大规模优化问题的几种方法 [D].长沙：湖南大学，2007．

[2] Bäck T.Evolutionary algorithms in theory and practice:evolution strategies，evolutionary programming，genetic algorithms [J].Complexity，2013，2(4):26- 27．

[3] DAVID E，JOHN H.Genetic algorithms and Machine Learning[J].Machine Learning，1988，3(2/3)：95- 99．

[4] Kennedy J，Eberhart R.Particle swarm optimization [C]∥Proceedings of IEEE International Conference on Neural Networks，1995.Perth:IEEE，1995：1942- 1948．

[5] 李碧.协同进化算法及其应用 [M].北京：科学出版社，2013．

[6] YANG Z，KE T，XIN Y.Large scale evolutionary optimization using cooperative coevolution [J].Information Sciences，2008，178(15):2985- 2999．

[7] LI X，YAO X.Cooperatively coevolving particle swarms for large scale optimization [J].IEEE Transactions on Evolutionary Computation，2012，16(2):210- 224．

[8] YANG Z，TANG K，YAO X.Differential evolution for high- dimensional function optimization [C]∥Proceedings of IEEE Congress on Evolutionary Computation，2007.Singapore：IEEE，2007：3523- 3530．

[9] REN Y，WU Y.An efficient algorithm for high-dimensional function optimization [J].Soft Computing，2013，17(17)：995- 1004．

[10] VESTERSTROM J，THOMSEN R.A comparative study of differential evolution，particle swarm optimization，and evolutionary algorithms on numerical benchmark problems [C]∥Proceedings of IEEE Congress on Evolutionary Computation，2004.Portland：IEEE，2004:267- 282．

[11] TANG K，LI X，SUGANTHAN P N，et al.Benchmark functions for the CEC’2010 special session and competition on large scale global optimization [R].Hefei:University of Sciece and Techndogy of China,2009．

[12] MAHDAVI S，SHIRI M E，RAHNAMAYAN S.Metaheuristics in large-scale global continues optimization：a survey [J].Information Sciences，2015，295:407- 428．

[13] DAS S，SUGANTHAN P N.Differential evolution:a sur-vey of the state-of-the-art [J].IEEE Transactions on Evo-lutionary Computation，2011，15(1):4- 31．

[14] 姚新，陈国良.模拟退火算法及其应用 [J].计算机研究与发展，1990(7)：1- 6． YAO Xin，CHEN Guo- liang.Simulated annealing algorithm and its applications [J].Journal of Computer Research and Development，1990(7):1- 6．

[15] MOLINA D，LOZANO M，SNCHEZ A M，et al.Meme-tic algorithms based on local search chains for large scale continuous optimisation problems：MA- SSW- Chains [J].Soft Computing，2011，15(11):2201- 2220．

[16] QIN A K，SUGANTHAN P N.Self- adaptive differential evolution algorithm for numerical optimization [C]∥Proceedings of The 2005 IEEE Congress on Evolutionary Computation，2005.Edinburgh：IEEE，2005:1785- 1791．

[17] YANG Z，TANG K，YAO X.Multilevel cooperative coevolution for large scale optimization [C]∥Proceedings of Evolutionary Computation.Hongkong：IEEE，2008:1663- 1670．

[18] YANG Z，TANG K，YAO X.Self- adaptive differential evolution with neighborhood search [C]∥Proceedings of Evolutionary Computation.Hongkong：IEEE，2008：1110- 1116．

[19] 王忠贵，罗亚中.高维复杂函数的混合模拟退火全局优化策略 [J].计算机工程与应用，2004，40(23)：36- 39． WANG Zhong- gui，LUO Ya- zhong.SA- based hybrid global optimization approach for complex functions with high- dimension [J].Journal of Computer Research and Development，2004，40(23):36- 39．

[20] FIGIELSKA E.A genetic algorithm and a simulated annealing algorithm combined with column generation technique for solving the problem of scheduling in the hybrid flowshop with additional resources [J].Computers & Industrial Engineering，2009，56(1):142- 151．

[21] HWANG S F，HE R S.A hybrid real- parameter genetic algorithm for function optimization [J].Advanced Engineering Informatics，2006，20(1):7- 21．

[22] 杨艳霞.一种基于模拟退火操作的混合差分进化算法 [J].智能系统学报，2014(1)：109- 114． YANG Yan- xia.A hybrid differential evolutionary algorithm based on the simulated annealing operation [J].CAAI Transactions on Intelligent Systems，2014(1):109- 114．

[23] LAND M W S.Evolutionary algorithms with local search for combinatorial optimization [J].Mechanical Engineering，1999，126(2):857- 893．

[24] MOLINA D，LOZANO M，HERRERA F.MA-SW-Chains：memetic algorithm based on local search chains for large scale continuous global optimization [C]∥Proceedings of Evolutionary Computation.Barcelona：IEEE，2010:1- 8．

[25] 刘瑞江，张业旺，闻崇炜，等.正交试验设计和分析方法研究 [J].实验技术与管理，2010，27(9):52- 55． LIU Rui-jiang，ZHANG Ye-wang，WEN Chong-wei，et al.Study on the design and analysis methods of orthogonal experiment [J].Experimental Technology and Ma-nagement，2010，27(9):52- 55.

A Hybrid Differential Evolution Algorithm with Multiple Search Strategies for Large-Scale Optimization

LUOJia-xiangNIXiao-yeHUYue-ming

(School of Automation Science and Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)

Large-scale optimization problem with multiple peaks and high dimension is a hot topic in current optimization research field.By using the co-evolutionary algorithm as the framework, this paper proposes a hybrid diffe-rential evolution (DE)algorithm with multiple search strategies to solve the large-scale optimization problem.In this algorithm, firstly, based on the thought of decomposition, a self-adaptive DE operator is applied to a local optimization of sub-problems.Then, a random search mechanism based on simulated annealing is introduced to improve the algorithm’s global search ability,and a local search chain is combined to search the solution space deeply.Finally, a set of benchmark functions is employed to evaluate the proposed algorithm.The results show that the algorithm is prior to the existing ones because it helps obtain better average value and optimized solution.

large-scale optimization; co-evolutionary algorithm; simulated annealing; differential evolution; local search

2016- 06- 30

国家科技重大专项(2014ZX02503- 3);国家自然科学基金资助项目(61573146);华南理工大学中央高校业务经费专项资金资助项目(2015ZZ0100) Foundation items: Supported by the National Science and Technology Major Project of the Ministry of Science and Technology of China(2014ZX02503- 3)and the National Natural Science Foundation of China(61573146)

罗家祥(1979-),女,博士,副教授,主要从事电子制造工业以及实际生产过程中的生产与优化调度、智能优化方法研究.E-mail:luojx@scut.edu.cn

1000- 565X(2017)03- 0097- 07

TP 18

10.3969/j.issn.1000-565X.2017.03.014