对称局部保持的半监督维数约简算法*

徐金成

(广东司法警官职业学院 信息管理系， 广东 广州 510520)

对称局部保持的半监督维数约简算法*

徐金成

(广东司法警官职业学院 信息管理系， 广东 广州 510520)

针对自然界较多图像具有对称的特点以及数据分布大多呈一定的流形结构情况,提出了一种对称局部保持的半监督维数约减(SLPSDR)算法.该算法使用矩阵定义维数约减映射矩阵元素之间的关系,使图像中对称的像素点对应的映射矩阵的值之间的差别最小;同时为了利用无标签训练样本保持数据的流形结构,要求低维空间中每个点的邻域关系与高维空间中的邻域关系相似.在CMU PIE、Extend YaleB、ORL、AR人脸数据库上的实验结果表明,图像数据明显的对称特点使得SLPSDR算法优于其他对比的维数约减算法.

对称限制;半监督学习;维数约简;人脸识别

维数约减的目的是将高维数据映射到低维空间，克服由“小样本、高维度”引起的维数灾难问题，提高模式识别系统的运行速度和执行效果.根据训练数据提供的标签情况，目前常见的维数约减算法可分为三类:有监督维数约减算法、半监督维数约减算法和无监督维数约减算法.其中只有半监督维数约减算法能够在提供无标签训练样本和有标签训练样本的情况下进行综合考虑，故文中着重研究半监督维数约减算法．

视觉信息是人们日常生活中非常重要的一部分，目前视觉信息处理已经在机器人、多媒体检索、人脸识别、物体识别等领域有着广泛的应用.在视觉信息处理中，数据经常有对称的特点，如果能够利用样本的对称信息，显然可以提高半监督维数约简算法的效果.目前对维数约简算法的研究可以分为三类:

(1)定义新的优化目标.王雪松等[1]提出了一种基于图的半监督判别局部排列降维方法，该方法在低维空间中不同类近邻点的分散度最大，而同类近邻点的分散度最小.兰远东等[2]通过最小化样本到其所属类别中心点之间的距离得出其邻域的拓扑结构，再通过最大化不同类别边缘间的距离来增强类别间的分离度.Wei等[3]提出了一种结合局部和全局拓扑结构的半监督维数约简算法，该算法通过最小化类内距离和类间距离来突出分类结构，局部拓扑结构通过最小化局部重构误差实现，全局拓扑结构通过最大化不在邻域的样本之间的距离实现.Yan等[4]为一些常见的维数约简提出了一个总体框架，在该框架下还提出了一种最大间隔Fisher分析维数约简算法，该算法使用一个样本与该样本同类的邻域之间的距离定义类内紧凑程度，并使用一个样本与该样本不同类的邻域之间的距离来定义类间分离程度.He等[5]提出了一种局部投影保持算法，该算法使用邻域信息构建图，使用图的拉普拉斯算子计算装换矩阵，能将数据映射到低维空间．

(2)定义新的流形结构.Ma等[6]提出了一种局部流形学习的方法用于构建邻域图，该方法发现稀疏表示方法有非常显著的分类效果，利用样本之间的稀疏系数构建样本之间的关系.Huang等[7]提出了一种全局局部保持的维数约简算法，该算法使用薄板样条和径向基核拟合数据的流形结构，能够捕获到步态中的动态和静态特征.Xing等[8]通过融合多种局部集合信息来获得可信度更高的流形结构.赵春晖等[9]提出了一种基于稀疏表示理论的且无需考虑近邻参数的半监督局部稀疏嵌入算法，该算法先通过求解范数优化问题来构建稀疏系数图，再利用有限的标签数据最大化类间信息.王宪保等[10]提出了一种半监督等距映射算法，该算法使用训练样本的标签样本构建K连通图，得到近似样本间测地线距离，并把它作为矢量特征代替原始数据点;然后通过测地线距离计算核矩阵，用半监督正则化方法代替多维尺度分析算法处理矢量特征;最后利用正则化回归模型构建目标函数，得到低维表示的显式映射．

(3)使用新的方法定义样本的邻域.杨格兰等[11]提出了等式融合的方法，并用此方法获得的标记传播算法的结果来映射初始数据，然后寻找最后的半监督降维结果，最逼近初始映射的数据结果只在图谱张成的线性空间中寻找.张云强等[12]观察到磨粒图像的数字化特征，估计高维特征空间中样本的密度是通过使用Parzen窗来实现，然后根据各个样本密度自适应调整邻域参数，再根据得出的邻域参数生成成对约束集.Huang等[13]提出了一种重构判别分析方法，该方法通过最小化类内重构误差和最大化类间重构误差，与传统的基于重构误差的方法相比，该方法能根据数据自适应设置一些邻域参数，并且能为每个样本估算最近异构类.Zhou等[14]提出了一种流形结构分区判别分析方法，该方法仅在局部流形结构变化的方向上计算类内相似度，能够很好地区分离得比较近但属于不同类的样本．

上述方法基本上都是通过定义新样本之间的关系来提高半监督维数约简的效果，忽略了样本维度上的先验知识.而样本维度上的先验知识已被用在其他机器学习方法中，如邓楠等[15]提出的基于稀疏表征多分类器融合的遮挡人脸识别方法，先对人脸进行多分辨率分块，再求取各子块稀疏表征分类器的识别率并确定其权重；Xu等[16]将原始图及其对称图作为训练数据，以训练效果更佳的分类器；Xu等[17]使用迭代方法发现了人脸图像的对称轴，将该方法作为人脸识别的预处理方法，可以提高数据的质量.显然上述方法没有同时利用数据维度上的先验知识与数据的其他先验知识.文中通过改进维数约简算法的优化目标，同时使用数据维度上的先验知识和其他先验知识，并由此提出了一种对称局部保持的半监督维数约简(SLPSDR)算法．

1 线性判别分析和拉普拉斯特征映射

1.1 线性判别分析

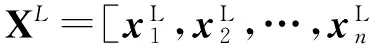
(1)计算样本的类内距离dW和类间距离dB，

(1)

(2)

式中，Nc为类的个数，u为样本均值，ui为第i类样本Ci的均值，ni为第i类样本的个数．

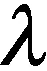
(3)使用Y=WTX将数据从高维空间映射到低维空间．

1.2 拉普拉斯特征映射

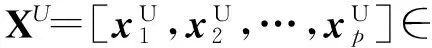
(1)构造一个q近邻图SM，其中基于0- 1权重的图的构造方法为

(3)

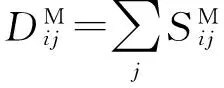
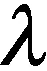
2 SLPSDR算法描述

2.1 视觉信息处理中的对称现象及其保持

很多视觉信息处理都是在对称图像上运行的，如人脸识别等.如图1所示，在人脸数据识别中，人脸明显具有左右对称的特点.在这种情况下，一个图像样本本身有非常明显的对称特征，如果在图像维数约简时能够考虑到图像的这种特点，显然可以提升维数约减的效果．

图1 ORL数据库部分图像[20]

以一个4×4的图像示例(如图2所示)为例，图中的数字表示图像转换成向量时各个像素点在向量中的下标，第i幅图像转换之后的向量记为xi.如果图像对称，那么有

xij=xi(16-j+1),j=1,2,…，16

(4)

图2 图像中像素点与其向量下标的关系

Fig.2 Relationship between the pixel and its vector subscript in image

要使图像在维数约简时能够考虑到图像的对称性，那么就需要实现对称的两个像素点经过投影之后的值应该也相近的目标.该目标可通过下式实现:

(5)

将式(4)代入式(5)可得

(6)

根据矩阵相乘原理，可将式(6)表示为

(7)

其中，Ak是维度为16的向量，前8个元素为1，后8个元素为-1.式(4)-(7)可以容易地推广到样本维度为m的情形:将式(4)-(6)中的16替换成m，将式(7)中的Ak替换成维度为m的向量，其中Ak中前m/2个元素为1，后m/2个元素为-1.这样通过式(7)即可实现对称的两个像素点经过投影之后的值应该也相近的目标．

1-10月，在公司化工原辅料、煤炭、材料、动静设备、电气仪表及配件库存物资中，动静设备资金量占仓库库存账面物资69%。其中，压缩机配件、汽轮机水轮机配件及工业泵配件等特殊储备占据24.9%。从控制效果看，5月煤炭和备件占用少，控制最好。公司对比标杆找差距，用“纵尺”和自己较真，制定报废处置尿素装置旧备品备件。

2.2SLPSDR算法的目标函数及其优化

SLPSDR算法对样本进行维数约简的主要目的是提高分类效果，所以样本通过SLPSDR算法映射到低维空间后需要能突出类别结构．

根据线性判别分析的原理可将SLPSDR算法的目标函数表示为[21]

(8)

根据拉普拉斯特征映射的原理可将其目标函数表示为

(9)

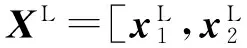
(10)

D=WTdBW

(11)

(12)

F=WTXLMXTW

(13)

(14)

式中:a、b为两个平衡参数，用于平衡突出类别结构，保持数据的流形结构及映射矩阵能够体现数据对称特点对目标函数的影响力;X=[XL,XU]，表示X由有标签训练数据和无标签训练数据组成;LM=DM-SM,

(15)

i,j=1,2,…,n+p；N(xi)、N(xj)表示符合条件的图.式(15)与式(3)略有差别，这是因为式(15)在计算时同时用到有标签训练数据和无标签训练数据，而式(3)只用到无标签训练数据．

显然，最大化trD与最小化trE可以突出样本通过SLPSDR映射到低维空间后的类别结构，有利于分类.最小化trF可以最小化高维空间相互之间有关系的样本在低维空间之间的距离.最小化trG可以最小化对称的两个像素点对应的投影矩阵的值之间的差别．

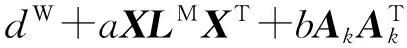
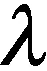
(16)

将特征值从大到小排序，选取前k个特征值对应的特征向量(w1,w2,…，wk)构成m×k的映射矩阵W．

2.3SLPSDR算法描述

输出:映射矩阵W

根据式(11)-(14)计算D、E、F、G;

计算式(16)的特征值和特征向量，将特征值从大到小排序，选取前k个特征值对应的特征向量(w1,w2,…,wk)构成m×k的映射矩阵W．

3 实验及结果分析

文中使用以下4个数据集进行实验:①CMUPIE人脸数据集[20]，包括68人的41 368幅脸部图像;②ExtendedYaleB人脸数据集[22]，包含38人，每人64幅人脸图像;③ORL人脸数据集[23]，包括40人的400幅人脸图像;④AR人脸数据集[24]，包含126人的4 000幅人脸图像.以上所有图像均裁剪放缩为32×32大小．

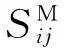
(17)

对比算法可以分成三类:无监督维数约简算法(如PCA)、有监督维数约简算法(如LDA)及半监督维数约减算法(如LGS3DR、SSMDELPDR、SLPSDR)．

半监督维数约简算法中训练数据包含有标签训练数据和无标签训练数据，其中有标签训练数据从每个类别分别随机选取3个或者6个，无标签训练数据从每个类别随机选取3个，剩余的样本作为测试样本.所有实验均执行50次，计算50次实验结果的平均值作为每个实验的最终结果.维数约简后子空间的维度K的取值范围为20～160，步长为20.实验结果采用准确度评价．

实验1 有标签训练数据从每个类别随机选取3个，无标签训练数据从每个类别剩余的数据中随机选取3个，其他数据为测试样本.6种算法在4个人脸数据库上的分类结果见表1，6种算法在4个数据库上投影到不同维度时的分类准确度见图3，其中图3(a)、3(b)、3(d)中只显示5条曲线，原因是PCA算法的分类准确度相对其他算法过低，如果将PCA算法的曲线也显示出来，其他算法的曲线之间的区分度非常小(图4(a)、4(b)、4(d)只显示5条曲线的原因同此)．

表1 实验1中几种算法在4个数据库上的最大分类准确度

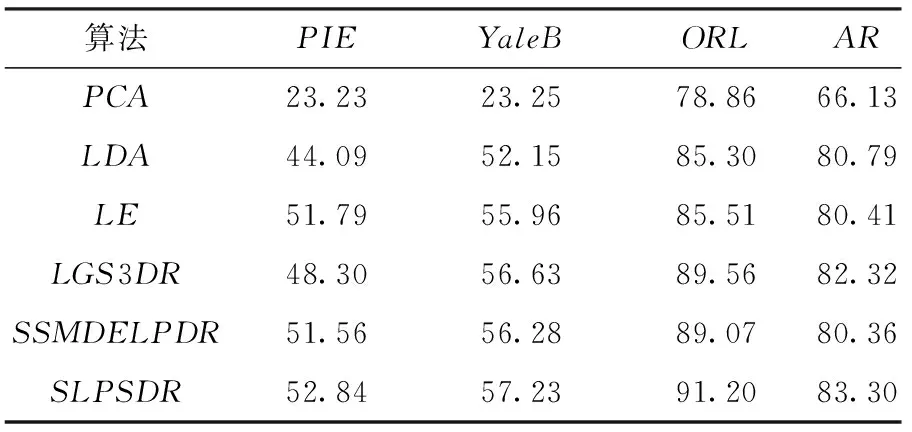
Table 1 Maximal classification accuracy of several algorithms on four databases in Experiment 1 %

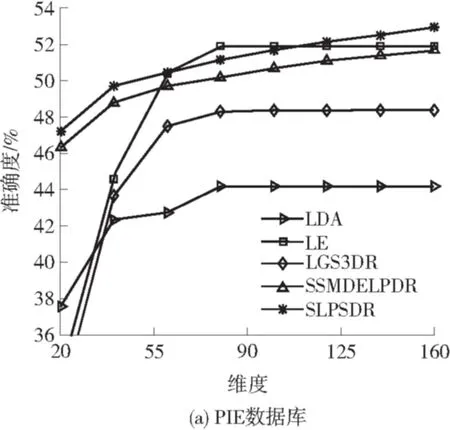
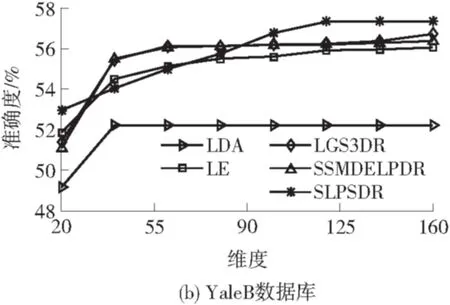
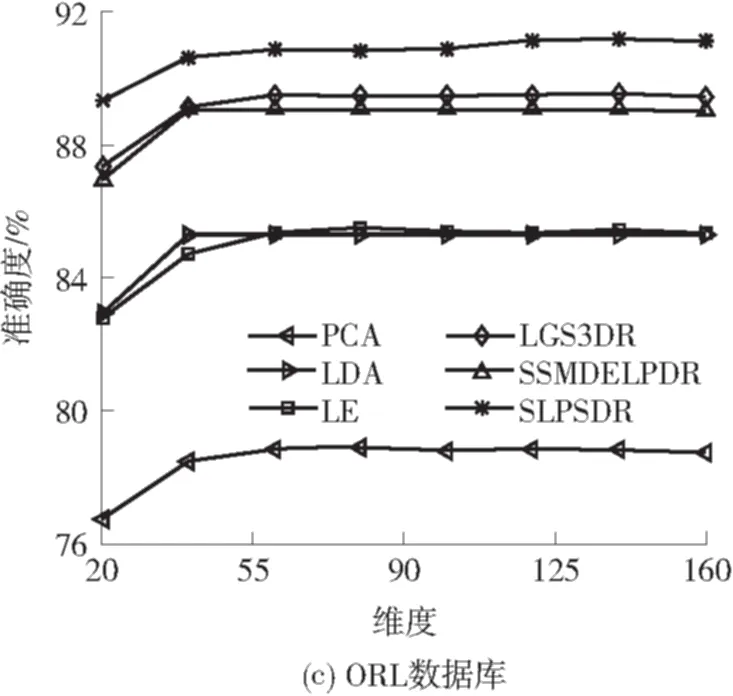
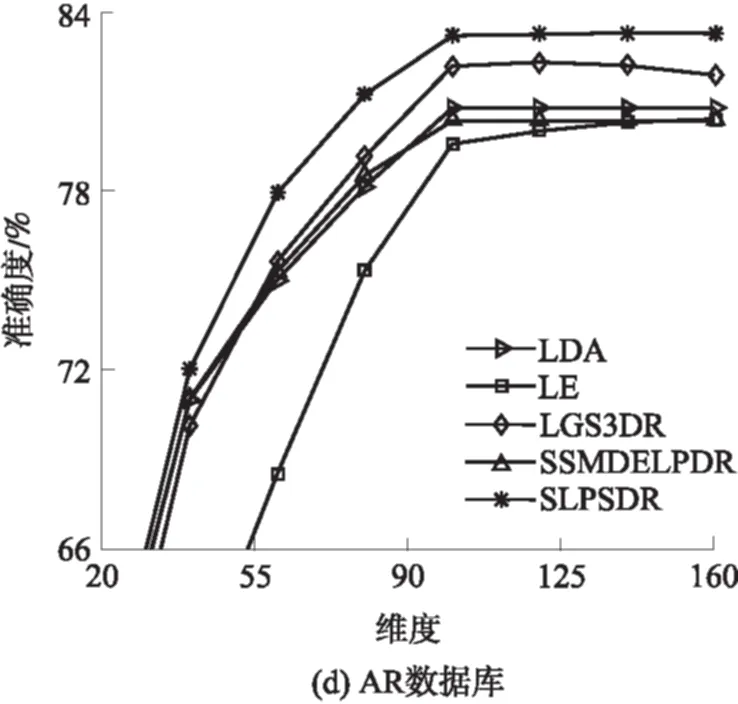
图3 实验1的实验结果

从表1可知，SLPSDR算法在4个数据库上的最大分类准确度比第二好的实验结果分别高1.05%、0.60%、1.64%、0.98%，这证明了SLPSDR算法的有效性.

从图3可知:在PIE、ORL、AR数据库上，SLPSDR算法在较低维度上就能达到较高的分类准确度，这在对速度要求非常高的应用环境中，可以将数据投影到更低的维度，以加快算法的执行速度;SLPSDR算法能在较多的维度上取得较为稳定的分类准确度，更有利于在实际应用中选择合适的投影子空间维度K．

实验2 有标签训练数据从每个类别随机选取6个，无标签训练数据从每个类别剩余的数据中随机选取3个，其他数据为测试样本.6种算法在4个数据库上的最大分类准确度见表2，6种算法在4个数据库上投影到不同维度时的分类准确度见图4.从表2可知，SLPSDR算法在4个数据库上的最大分类准确度比第二好的实验结果分别高0.63%、1.10%、1.55%、0.80%，证明了SLPSDR算法的有效性．

Table 2 实验2中几种算法在4个数据库上的最大分类准确度

Table 2 Maximal classification accuracy of several algorithms on four databases in Experiment 2 %

从图4可知:在PIE、ORL、AR数据库上，SLPSDR算法在较低维度上就能达到较高的分类准确度;SLPSDR算法能在较多的维度上取得较为稳定的分类准确度．

4 结论

考虑到视觉信息处理中大部分数据都有对称的特点，文中定义了一种新的优化目标，使得在优化后对称像素点对应的维数约简矩阵的元素点之间的差别最小，提出了基于线性判别分析和拉普拉斯特征映射的半监督维数约减算法.实验结果表明:文中算法在人脸识别上有较好的维数约简效果;文中算法能在更低维度上达到较好的维数约简效果，在较多的维度上均能获得较为稳定的分类准确度，能够应用于速度需求较快的环境以及在现实应用中能够较容易地选择合适的投影子空间维度K.文中算法在设计目标函数时没有考虑到可能造成对称像素点的坐标位置并不完全对称的一些干扰因素，故如何设计目标函数使之能克服干扰因素的影响是进一步的研究内容．

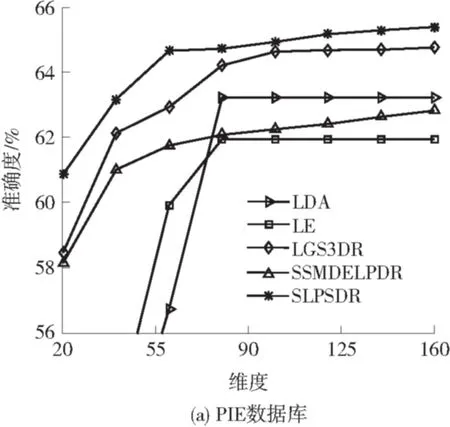
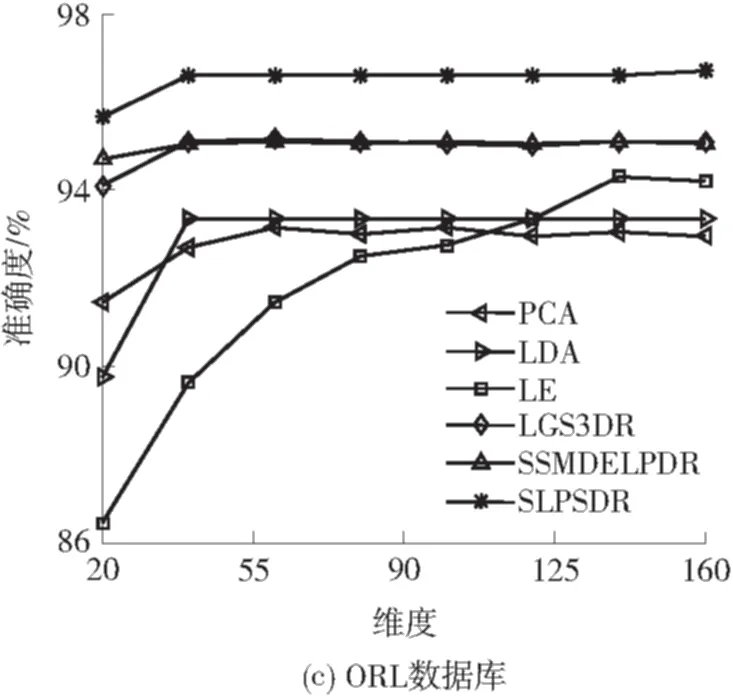
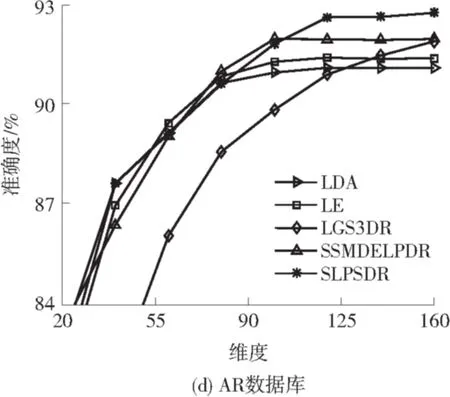
图4 实验2的实验结果

[1] 王雪松，胡汇涓，程玉虎.遥感影像的半监督判别局部排列降维 [J].电子学报，2014，42(1):84- 88. WANG Xue-song，HU Hui-juan，CHENG Yu-hu.Dimensionality reduction of remote sensing image using semi-supervised discriminative locality alignment [J].Acta Electronica Sinica，2014，42(1):84- 88．

[2] 兰远东，高蕾，曾少宁，等.半监督边缘判别嵌入与局部保持的维度约简 [J].计算机系统应用，2014，23(10):138- 141． LAN Yuan-dong，GAO Lei，ZENG Shao-ning，et al.Semi supervised marginal discriminant embedding and local preserving for dimensionality reduction [J].Computer Systems & Applications，2014，23(10):138- 141．

[3] WEI Jia，ZENG Qun-fang，WANG Xuan.Integrating local and global topological structures for semi-supervised dimensionality reduction [J].Softcomputing，2014，18(6):1189- 1198．

[4] YAN Shuicheng，XU Dong，ZHANG Benyu，et al.Graph embedding and extensions：a general framework for dimensionality reduction [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2007，29(1):40- 51．

[5] HE Xiaofei，NIYOGI P.Locality preserving projections [C]∥Advances in Neural Information Processing Systems 16.Vancouver：Neural Information Processing Systems Foundation，Inc，2003：585- 591．

[6] MA Li，CRAWFORD M M，YANG Xiaoquan，et al.Local-manifold-learning-based graph construction for semisupervised hyperspectral image classification [J].IEEE Tran-sactions on Geoscience and Remote Sensing，2015，53(5):2832- 2844．

[7] HUANG Sheng，ELGAMMAL A，LU Jiwen，et al.Cross-speed gait recognition using speed-invariant gait templates and globality：locality preserving projections [J].IEEE Transactions on Information Forensics And Security，2015，10(10):2071- 2083．

[8] XING Xianglei，WANG Kejun，LV Zhuowen，et al.Fusion of local manifold learning methods [J].IEEE Signal Processing Letters，2015，22(4):395- 399．

[9] 赵春晖，崔晓辰，齐滨.高光谱图像半监督局部稀疏嵌入降维算法 [J].沈阳大学学报(自然科学版)，2014，26(6):462- 467． ZHAO Chun-hui，CUI Xiao-chen，QI Bin.Dimensionality reduction algorithm of remote sensing image using semi- supervised local sparse embedding [J].Journal of Shen-yang Universtiy(Natural Science Edition)，2014，26(6):462- 467．

[10] 王宪保，陈诗文，姚明海.基于正则化的半监督等距映射数据降维方法 [J].电子与信息学报，2016，38(1):241- 245． WANG Xian-bao，CHEN Shi-wen，YAO Ming-hai.Data dimensionality reduction method of semi-supervised isometric mapping based on regularization [J].Journal of Electronics & Information Technology，2016，38(1):241- 245．

[11] 杨格兰，金辉霞，孟令中，等.基于图的半监督降维算法 [J].计算机科学，2014，41(4):280- 282，296． YANG Ge-lan，JIN Hui-xia，MENG Ling-zhong，et al. Graph-based semi-supervised dimensionality reduction algorithm [J].Computer Science，2014，41(4):280- 282，296．

[12] 张云强，张培林.基于半监督局部保持投影的磨粒图像特征降维 [J].中南大学学报(自然科学版)，2015，46(8):2937- 2943. ZHANG Yun-qiang，ZHANG Pei-lin.Feature dimensio-nality reduction of wear particle images based on semi-supervised locality preserving projection [J].Journal of Central South University(Natural Science Edition)，2015，46(8):2937- 2943．

[13] HUANG Pu，GAO Guangwei.Parameterless reconstructive discriminant analysis for feature extraction [J].Neurocomputing，2016，190：50- 59．

[14] ZHOU Yang，SUN Shiliang.Manifold partition discriminant analysis [J].IEEE Transactions on Cybernetics，2016，doi：10.1109/TCYB.2016.2529299/1- 11．

[15] 邓楠，徐正光，王珺.基于稀疏表征多分类器融合的遮挡人脸识别 [J].计算机应用研究，2013，30(6):1914- 1916．

DENG Nan，XU Zheng-guang，WANG Jun.Sparse repre-sentation based multi-classifier fusion approach for occlu-ded face recognition [J].Application Research of Compu-ters，2013，30(6):1914- 1916．

[16] XU Y，ZHU X，LI Z，et al.Using the original and ‘symmetrical face’ training samples to perform representation based two-step face recognition [J].Pattern Recognition，2013，46(4):1151- 1158．

[17] XU Yong，ZHANG Zheng，LU Guangming，et al.Appro-ximately symmetrical face images for image preprocessing in face recognition and sparse representation based cla-ssification [J].Pattern Recognition，2016，54：68- 82．

[18] MARTINEZ A M，KAK A C.PCA versus LDA [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23(2):228- 233．

[19] BELKIN M，NIYOGI P.Laplacian eigenmaps for dimensionality reduction and data representation [J].Neural Computation，2003，15(6):1373- 1396．

[20] SIM T，BARKER S，BSAT M.The CMU pose，illumination，and expression database [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2003，25(12):1615- 1618．

[21] 施展，杜明辉，梁亚玲.基于2DNPP和Trace变换的平面内旋转人脸识别 [J].华南理工大学学报(自然科学版)，2012，40(8):46- 50． SHI Zhan，DU Ming-hui，LIANG Ya-ling.In-plane rotary face recognition based on 2DNPP and Trace transform [J].Journal of South China University of Technology(Natural Science Edition)，2012，40(8):46- 50．

[22] GEORGHIADES A S，BELHUMEUR P N，KRIEGMAN D J.From few to many：illumination cone models for face recognition under variable lighting and pose [J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2001，23(6):643- 660．

[23] SAMARIA F S，HARTER A C.Parameterization of a stochastic model for human face indenfication [C]∥Proceedings of IEEE Workshop on Applications of Computer Vision.Sarasota：IEEE，1994：138- 142．

[24] MARTINEZ A，BENAVENTE R.The AR face database[R].Madrid：Instituto San Isidro，1998．

[25] CHANG Chih-Chung，LIN Chih-Jen.LIBSVM：a library for support vector machines [J].ACM Transactions on Intelligent Systems and Technology，2011，3(2):1- 27．

(责任编辑：许花桃)

A Symmetric Locally-Preserving Semi-Supervised Dimensionality Reduction Algorithm

XUJin-cheng

(Department of Information Management，Guangdong Justice Police Vocational College，Guangzhou 510520，Guangdong，China)

As many natural images are symmetrical and most of data distributions exhibit a manifold structure, a symmetric locally-preserving semi-supervised dimensionality reduction (SLPSDR) algorithm is proposed. In the algorithm, a matrix is used to define the relationship between dimensionality reduction mapping matrix elements, so as to minimize the difference between the matrix elements of symmetric pixel points in an image. In order to keep the manifold structure of data by using the training samples without a label, it is required that the neighborhood relationship of each point in a low-dimension space is similar to that in a high-dimension space. The experimental results on CMU PIE, Extend YaleB, ORL and AR face databases show that the symmetric feature of image data causes the SLPSDR algorithm to be superior to other contrastive dimensionality reduction algorithms.

symmetry constraint; semi-supervised learning; dimensionality reduction; face recognition

2016- 04- 18

国家自然科学基金资助项目(61402118) Foundation item: Supported by the National Natural Science Foundation of China(61402118)

徐金成(1982-),男,讲师,主要从事图像处理、模式识别研究.E-mail:79742144@qq.com

1000- 565X(2017)03- 0089- 08

TP 391

10.3969/j.issn.1000-565X.2017.03.013