轴流叶片非接触式模态特性测试系统的开发与研究
2017-06-21宁宝奇李朝峰杨树华孟继纲李凯华
宁宝奇 ,李朝峰 ,杨树华 ,孟继纲 ,李凯华
(1.东北大学机械工程与自动化学院,沈阳110819;2.大连理工大学能源与动力学院,大连116024;3.沈阳鼓风机集团股份有限公司,沈阳110819)
0 引言
轴流叶片是旋转压气做功类设备的核心零部件,其模态特性分析一直是研究人员所关注的重点[1-2],而叶片数值模型仿真结果的准确性离不开测试实验的佐证。在工程应用中,研究人员采用各种模态测试方法测试结构的振动模态来验证结构设计的正确性[3-6]。以往的叶片模态测试大多采用锤击的方法进行,其振动信号的衰减特性会导致高频处的测试不准确甚至无法测到。随着叶片结构轻量化和动力性能需求的提升,结构的中高频动响应越来越突出。如果能在结构设计阶段对动态响应进行预示,并根据预示结果进行结构优化,则能够从本质上解决高周疲劳的问题,因此对叶片在高频激励下的响应测试变得越来越重要。对于轴流转子叶片的模态测试,目前国内外普遍采用的是锤击法。该方法自20世纪80年代就已经成为频域法测试叶片动态特性的主要途径[7-8]。与锤击法相比,时域共振法理论上可以真实地反映出结构在不同激振频率下的响应,由于该方法的测试频率范围宽,可识别的模态信息丰富,因此具有十分明显的优越性。当前的虚拟仪器技术的发展使得实现持续扫频及非接触激励的控制变为可能。因此轴流叶片的时域共振测试具备一定的工程和理论意义。
针对模态识别方法问题,有很多学者作了大量工作。边杰[9]提出了1种利用相频曲线在共振点的切线斜率求解模态阻尼比的新方法,即切线斜率法,由共振点处的切线斜率来确定模态阻尼比。Tarinejad等人[10]提出了基于FDD-wavelet方法的结构模态识别新算法,并指出了该算法在多种动态系统中的适用性和准确性。李晖等人[11-12]在明确阻尼辨识原理的基础上,对经典的半功率带宽阻尼识别方法进行了改进,提出了1种在频域上识别阻尼参数的新方法。刘红石[13]比较分析了几种确定Rayleigh阻尼比例系数的方法,并从相对误差理论的角度应用最小二乘法导出了Rayleigh阻尼比例系数的计算公式。而针对测试软件的开发,虚拟仪器由于具有开发灵活和成本低等优点而被广泛采用。Ladipo等人[14]通过LabVIEW程序监测多自由度系统的振动幅度,主动调节减振器,对振动形成了有效的控制。Shah等人[15]提出了用Lab-VIEW系统化的方式在实时系统中测量振动信号,监测和预先判断旋转机械出现的故障。因此,基于LabVIEW开发测试软件是1个很好的选择。
为了拓宽被测试对象的有效测试频率范围,并提高其测试的准确性,本文基于时域共振法进行了轴流叶片模态特性测试系统的开发,实现了叶片的各阶固有频率及相应振型及模态阻尼比的测试,并给出了比例阻尼系数的估计值。在企业级实验工作中获得了良好的应用效果,为该类测试系统的开发与测试工作提供参考。
1 动力参数测试原理及数据处理办法
1.1 不同幅值表示下固有频率与共振频率的关系
叶片结构一般为多自由度系统,按照模态理论解耦后可变成若干单自由度系统。因而,这里以单自由度系统为例,推导激振力作用下叶片的响应。
固有频率是振动系统的重要特性参数。设激振力F0cosωt作用在有阻尼单自由度系统上,系统振动位移稳态解幅值可表示为
式中:k为刚度;m为振动质量;c为振动阻尼。将阻尼参变量n=c/2m,阻尼比ζ=n/ωn,无阻尼固有频率ωn=代入式(1),位移幅值可改写为
B在其极值时取得最大值。极值条件为
速度幅值为
同样可得到极值条件为
加速度幅值为
在2ζ2<<1时,可近似得到极值条件为
由式(3)、(5)和(7)可以看出,振动的位移、速度、加速度的幅值各自到达极大值的共振频率各不相同。当 ζ=0 时,由式(3)、(5)和(7)分别计算得到的固有频率都相等且等于系统的无阻尼自由振动频率,即固有频率;在弱阻尼条件下,3种共振频率都接近于系统的固有频率,但只有速度共振频率真正与固有频率相等。因此在本测试系统中采用非接触式激光速度测振仪进行信号的采集。
1.2 频域带宽法测试阻尼的原理
阻尼是反映结构系统振动过程中能量耗散特征的参数。对于振动系统的稳态解幅值式(1),代入无阻尼频率 ωn、阻尼比 ζ、频率比 r、静力 F0下的形变 δst,对式(1)作替换可得
对于小阻尼系统时,振幅放大系数(B/δst)取得最大值
在固有频率ωn左右取2个频率点ω1、ω2,且2点振幅放大系数相等,令 B/δst=p(B/δst)max(0 对于较小的 ζ值(ζ<0.05),式(10)的解可近似为 2个解的平方相减,利用近似关系ω1+ω2=2ωn进一步化简,则式(11)可变为 当比例值为半功率点,则式(12)变为 式(13)即为常用的半功率带宽法标准的辨识公式。 通常,结构阻尼矩阵C不能像质量矩阵M和刚度矩阵K那样可由单元体的阻尼矩阵形成,而采用C=αM+βK形式的粘性阻尼矩阵。这种阻尼称为Rayleigh阻尼,其阻尼矩阵称为比例阻尼矩阵。其中α、β为Rayleigh阻尼比例系数,C、M、K分别为阻尼矩阵、质量矩阵和刚度矩阵。 使用无阻尼系统的正则模态矩阵u对阻尼矩阵C对角化,即可得到 其中ζi为各阶模态阻尼比,ωi为各阶固有频率。 由最小二乘法可令 将式(15)分别对α、β求导,且令其偏导为0,化简可获得阻尼系数α、β分别为 由此得到各阶模态阻尼比与比例阻尼系数α、β之间的关系。因此,对结构进行动响应分析时,就可将按式(16)、式(17)求得的α、β作为最后动力响应计算的比例阻尼系数。 按照时域共振法的原理以及测试准确性的需求,需要对非接触式电磁激振器进行激振信号的输出控制,对非接触式激光拾振传感器进行拾振信号采集记录,对测得信号的数据进行提纯处理,模态特征提取,以及最终报告的生成。因此需将开发测试系统分为4个独立的模块,即参数配置模块、信号采集与滤波模块、模态数据提取模块和试验报告生成模块。模块化程序流程如图1所示。 根据软件总体架构中各个功能模块间的相互关系,调用各个模块功能。测试系统采用单点激励多点采集的方式,自定义设置扫频时间、扫频频率范围和激振力幅值,以线性正弦扫描扫频的方式激励叶片,同时采集均布在叶片上的各采样点的扫频频响曲线。将所有采样点处的振动响应信号进行实时处理。提取出响应信号中的混频信息,再在混频信息中提取出所关心的频率成分的单频信息(包括频率和幅值),生成频域响应曲线。所有采样点处的频域响应曲线组成模态分析图,依据模态识别原理,由程序自动在模态分析图中查找计算叶片的模态特性,其中包括各阶固有频率、振型、模态阻尼比和比例阻尼系数。最后在软件界面中显示识别出的模态特性,将结果数据保存在计算机硬盘中并生成测试报告。 在软件总体架构和基本操作流程确定后,还需要设计友好的软件界面,使人机之间的信息交流直观清晰,软件操作简单方便,逻辑清晰合理,提高工作效率。模态参量测试系统的部分工作界面如图2所示,其中图(a)为参数配置界面,图(b)为振动信号采集界面,图(c)为测试结果回放界面,图(d)为报表生成界面。每个功能模块都有与之对应的操作界面,工程人员可以通过改变界面上的输入量(如数据采集卡的采样率、采样数及扫频信息等)来调控测试系统完成相应的功能操作,同时软件分析计算出的测试结果也可以通过图形、图表、数字等形式直观地显示在软件界面中,达到模态特性测试的目的。 在激振器和拾振器工作的过程中,由于电子元件电流噪声的干扰,测得信号的频率成分往往十分复杂,尤其在高频和低频激励位置干扰更为明显,因此需要对信号进行滤波提纯处理。这里对常用的巴特沃斯(Butterworth)、切比雪夫(Chbyshev)、贝塞尔(Bessel)、椭圆4种IIR数字滤波器进行测试,它们在通带频带内外都有平稳的幅频特性。为获得较好的滤波效果,对50Hz激振频率下的信号进行带通滤波,以选择合适的滤波器,4种滤波器对50Hz激振频率下的信号进行带通滤波的效果对比(如图3所示)。其中图(a)、(b)为滤波前信号的时域及频谱,图(c)、(d)为4种滤波器滤波后信号的频率及幅值对比,图(e)、(f)为滤波器滤波后信号的时域。 从图(c)中可见,4种滤波器都能有效地滤掉杂频成分。但是从图(d)中可见Bessel滤波器滤波后信号的幅值较另外三者大,对信号的能量削弱较小,且图(e)所示的Bessel滤波器滤波后信号的整体幅频特性最好,图(f)的椭圆滤波器最差。因此Bessel滤波器是这4种滤波器中最好的选择。从图(e)、(f)中可见,滤波器有较长的过渡带,在过渡带上造成了信号失真,但过渡带之后的幅频特性非常好,因此在数据处理时需截取滤波后信号的后半部分进行后续分析,以消除失真对信号的影响。 根据既定的测试原理搭建的测试平台,如图4所示。为实现激励的非接触要求,根据需要从相关激振器厂家中选择国内某厂家定制了非接触式电磁激振器,并采用了某型数字采集卡。振动速度采集传感器为数字非接触式激光测振仪,该型传感器可避免因在叶片上粘贴传感器给叶片增加附加质量而带来的测量误差。该测振仪的速度分辨率为0.05μm/s(1Hz带宽),可以满足测试系统对速度信号精度识别的要求。根据Nyquist采样定理:如果在信号中不丢失任何信息,则采样频率必须大于信号中最高频率的2倍。在实验中需要分析的最大频率为11000 Hz,则所需的最小采样频率为11000 Hz×2.56=28200 Hz。实验中选取的采样频率为96000 Hz,远大于所需的最小采样率,可以满足Nyquist采样定理。 根据前面测试平台的搭建计划,选定实验对象为图5(a)所示的某型号轴流压缩机8级叶片,展长为63 mm,弦长为50 mm,翼厚比为8.7%~13.5%。搭建的实验现场如图5(b)所示。 扫描激励从理论上讲是1种瞬态激励的方法,扫描速度不合适将在一定程度上影响测量的准确性,因此需要对扫描速度进行选择。为了测得叶片各阶模态振型,这里在叶片上规划了5×6个采样点,并对采样点逐个进行扫描扫频激励,同时采集各个采样点的响应信号,提取响应信号中的频率成分信息,绘制频域响应曲线,并分析获得各阶固有频率、振型、模态阻尼比和比例阻尼系数等目标参数,最终根据需要输出实验报告。 由于实验室条件的限制,采用东华和LMS两种商用测试系统进行锤击法测试(实验现场如图6所示),并将测试结果及理论计算值与所述的测试系统得到的固有频率测试结果以及有限元计算结果进行对比验证。经过多次敲击测试,将得到的效果最好的几组频响数据与所述测试系统得到的模态分析图相对比(如图7所示)。由锤击法的频响图可以看出,11000 Hz之前有10个峰值,可以大致找到10阶固有频率,其中一些频率值识别比较困难。 从图7中可见,经过2型设备多次锤击实验测得的频响曲线、数值计算值以及所述的系统所测试的幅频曲线反映的频率值基本一致。但锤击法测试出现了漏频现象,高频处测试准确度和辨识度降低。这一现象是由于锤击法自身的缺陷造成的,且锤击法难以保证每次的敲击都具有相同的特性。锤击测试结果与本文所述的测试系统得到的固有频率测试结果以及有限元数值计算值的对比见表1。通过对比可以发现:2种方法得到的固有频率测试值与理论计算值基本一致,都处在相同的频率区间范围内;在2型设备的锤击法测试中,在第3阶处都出现了漏频现象,中高频处频响曲线所受干扰较大,准确识别固有频率比较困难;测试系统得到的测试结果无漏频现象,且在11000 Hz以内的固有频率都能准确的识别出来;本文所开发的测试系统得到的模态分析图包含的模态信息非常丰富,在高频处依然可以获得很好的响应特征,很好地克服了锤击法重复性差及高频衰减快的缺点。测试系统得到的测试结果与锤击法1和锤击法2的测试结果对比,最大相对误差都在0.6%以下,在理论上是由于瞬态激振和稳态激振2种不同的激励形式造成的。因此认为所开发的非接触式模态测试系统所测的结果是可信的。 表1 固有频率测试结果对比 通过上述实验验证发现:由于受到电磁激振器及采集卡性能的限制,通过线性扫描扫频所得到的叶片在50~11000 Hz范围内的幅频曲线是可信的。图8为30个测点对应的幅频曲线,从图中可以找到11个较为明显的波峰,峰值处所对应的频率值即为固有频率值。测试系统根据各阶频率的振动幅值绘制出的各阶固有频率下的振型如图9所示。通过试验测得的各阶固有频率值和对应的模态阻尼比见表2,以及由最小二乘法得到的比例阻尼系数,该比例阻尼系数值可对动力学计算工作提供一定程度上的参考。 表2 叶片模态特性测试结果 为了判定模态阻尼比以及比例阻尼系数的准确性,本文通过计算多次测量结果最大相对误差的方法来判定本测试系统测试模态阻尼比方法的可重复性。为了避免因采样点位置不同而造成的实验误差,保证每次都在相同点采样,每阶阻尼比都至少测量3次,部分测试结果对比见表3。由测试结果可以看出,每阶阻尼比3次测量结果的最大相对误差都不大于1%,证明本测试系统所应用的阻尼比测试方法具有较好的可重复性和一致性,模态阻尼比测试结果是可信的。根据测试得到的各阶固有频率和模态阻尼比计算比例阻尼系数α、β,再通过α、β及固有频率值计算各阶阻尼比,将阻尼比测试值和计算值进行对比得到相对误差。去除部分对模态贡献较小阶次的模态数据,测试结果对比见表4。由于该结果通过最小二乘法获得,且无法保证通过2个值来拟合所有阶的阻尼情况,该部分的误差值会稍大,结果的相对误差都在可接受的范围内,因此该测试系统所应用的比例阻尼系数计算方法是可靠的。 表3 模态阻尼比测试方法可重复性验证结果 表4 比例阻尼系数计算方法可靠性验证结果 应用NI LabVIEW平台,基于时域共振法和非接触式激励测量技术开发了针对轴流叶片中高频模态特性的测量系统,并实现了激振测振设备和信号分析系统的全自动驱动分析工作。具体工作包括: (1)推导了辨识模态阻尼比及比例阻尼系数的公式,比较了多种滤波器的滤波效果并选择合理的滤波器。详细说明了动力参数的测试原理及测试系统的构建。 (2)搭建了测试实验平台,对测试系统进行了实验验证。结果表明,本测试系统的测试频率范围为50~11000 Hz,可以实现轴流叶片的各阶(尤其在中高频处)固有频率、振型、模态阻尼比及比例阻尼系数的测试。并且测试过程更加自动化,测试的模态信息更加丰富。 (3)与锤击法固有频率测试结果及理论计算结果进行了对比,所得到的误差可以接受,证明了该测试系统具有可信性。测试避免了漏频现象,模态阻尼比和比例阻尼系数的测试计算均在可接受的范围内。研究结果表明,该测试系统的测频范围宽,精度高,具有良好的准确性和可重复性。 [1]Wang H,Ding JJ,Ma B,et al.The time domain analysis of the flutter of wind turbine blade combined with eigenvalue approach[J].Advanced Materials Research,2013,342-347. [2]Schlagwein G,Schaber U.Non-contact blade vibration measurement analysis using a multi-degree-of-freedom model[J].Journal of Power&Energy,2006,220(6):611-618. [3]Griffith T D,Carne T G,Paquette J A.Modal testing for validation of blade models[J].Wind Engineering,2008,32(2):91-102. [4]Mao H J.Modal testing and numerical simulation of large wind turbine blade[J].Journal of Engineering Thermophysics,2009,30(4):601-604. [5]Ewins D J,Weekes B,Carri A D.Modal testing for model validation of structures with discrete nonlinearities[J].Mathematical Physical&Engineering Sciences,2015,373(2051):1-18. [6]Damgaard M,Ibsen L B,Andersen L V,et al.Cross-wind modal properties of offshore wind turbines identified by full scale testing[J].Journal of Wind Engineering&Industrial Aerodynamics,2013,116(5):94-108. [7]李勋,张东明,赵开宁.锤击法在航空发动机部件模态试验中的常见问题浅析[J].航空发动机,2010,36(5):47-51.LI Xun,ZHANG Dongming,ZHAO Kaining.Common problems analysis of impact modal test in aeroengine component[J].Aeroengine,2010,36(5):47-51.(in Chinese) [8]Liu J,Gao J L,GuiZhi M U,et al.An improved experimental modal analysis system with hammering method[J].Journal of Vibration&Shock,2009,28(3):174-177. [9]边杰.共振点切线斜率估计模态阻尼的新方法[J].太原理工大学学报,2016(5):563-567.BIAN Jie.A novel for estimating modal damping with tangent slope value at resonant point[J].Journal of Taiyuan University of Technology,2016(5):563-567.(in Chinese) [10]Tarinejad R,Damadipour M.Modal identification of structures by a novel approach based on FDD-wavelet method[J].Journal of Sound&Vibration,2014,333(3):1024-1045. [11]李晖,孙伟,张永峰,等.悬臂薄板结构阻尼特性几种测试方法的比较[J].中国工程机械学报,2013,11(4):347-353.LI Hui,SUN Wei,ZHANG Yongfeng,et al.Comparative study on texting methods for damping property of cantilever thin-plate structures[J].Chinese Journal of Construction Machinery,2013,11(4):347-353.(in Chinese) [12]李晖,孙伟,徐凯,等.基础激励频域带宽法辨识悬臂薄板结构的阻尼特性[J].中国机械工程,2014(16):2173-2177.LI Hui,SUN Wei,XU Kai,et al.Damping characteristics of thin cantilever plate structure identified by frequency bandwidth method of base excitation [J].China Mechanical Engineering,2014(16):2173-2177.(in Chinese) [13]刘红石.相对误差与Rayleigh阻尼比例系数的确定 [J].湖南工程学院学报:自然科学版,2001,11(3,4):36-38.LIU Hongshi.The determination of relative error and the Rayleigh damping ratio[J].Journal of Hunan Institute of Engineering(Natural Science Edition),2001,11(3,4):36-38.(in Chinese) [14]Ladipo I L,Muthalif A G A.Wideband vibration control in multi degree of freedom system:experimental verification using LabVIEW[J].Procedia Engineering,2012,41:1235-1243. [15]Shah H S,Patel P N,Shah SP,et al.8 channel vibration monitoring and analyzing system using LabVIEW[C]//Nirma University International Conference on Engineering.Piscataway:IEEE Press,2014:1-4.1.3 Rayleigh比例阻尼系数的求解
2 测试系统的构建
2.1 系统框架及测试流程
2.2 系统交互界面设计
2.3 滤波器的选择
3 可信性的验证及实验结果
3.1 测试平台的搭建
3.2 测试可信性的验证
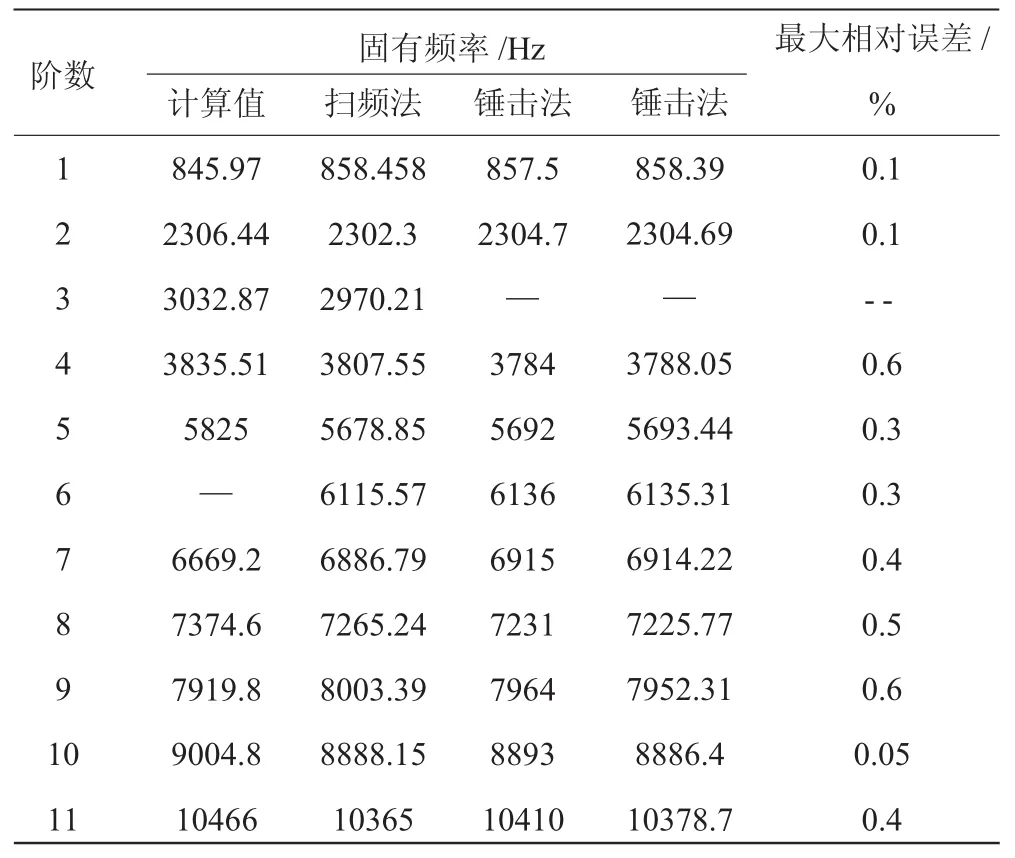
3.3 测试系统的实验测试结果
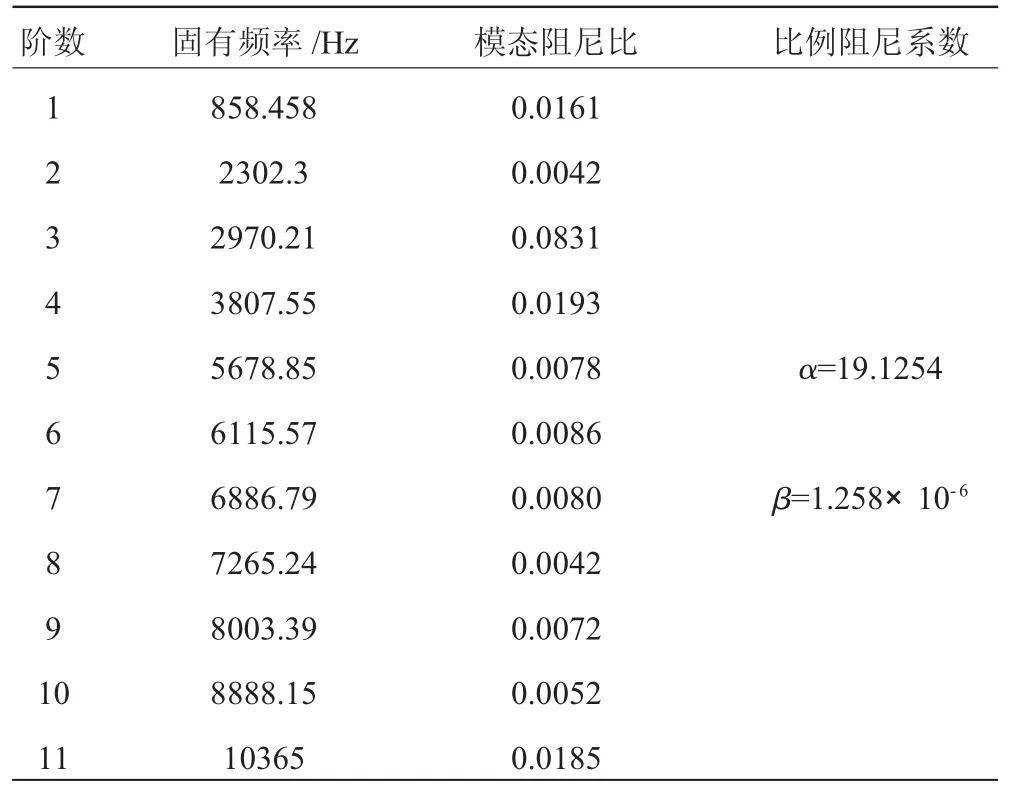
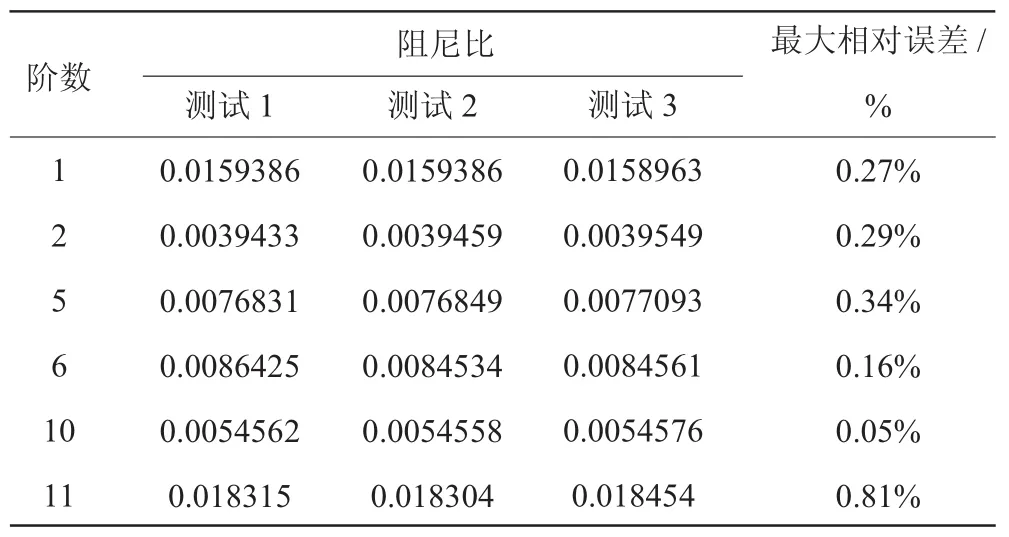
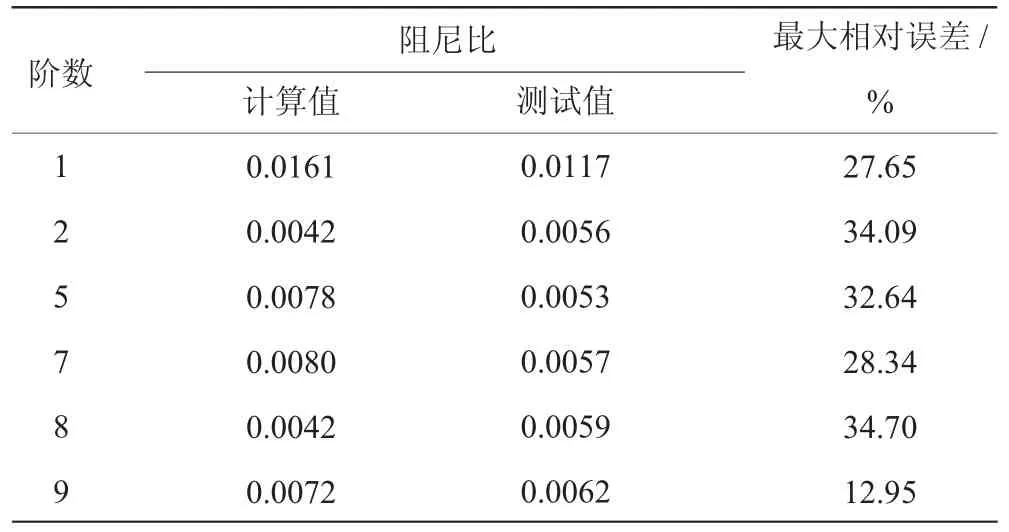
4 结论
