浅谈高考中幂.对数值比较大小
2017-06-20湖南省长沙市开福区周南中学李仙芝
湖南省长沙市开福区周南中学 李仙芝
幂式、对数式等数值比较大小问题,利用同底数、同指数或同真数等借助于函数单调性或图象求解.比较函数值的大小(1)同底幂比大小,则利用指数函数,同底对数比大小则利用对数函数的单调性进行比较;(2)当底数不同,指数也不同时,则需要引入中间量进行比较;对数值比较:当(a-1)(N-1)>0时,;当(a-1)(N-1)<0时,logNa<0,即底和真数在1同侧,对数值为正,1异侧对数为负;(3)对多个数进行比较,可用0或1或其它值作为为中介值进行比较(4). 当底数中含有字母时要注意分类讨论;下面介绍几种常见方法和题型。
基础方法1:同底对数式或同底指数式比大小,利用单调性;不可化同底找中介值比大小
例题1:(1)(文)设a=log954,b=log953,c=log545,则( )
A.a<c<b B.b<c<a
C.a<b<c D.b<a<c
[答案] D
[解析]∵y=log9x为增函数,∴log954>log953,∴a>b,又c=log545=1+log59>2,a=log954=1+log96<2,∴c>a>b,故选D.
变式:(1)已知a=21.2,

A.c<b<a
B.c<a<b
C.b<a<c
D.b<c<a
解析

c=2log52=log522<log55=1<20.8=b,
故c<b<a.
基础方法2:不同底能化同底的尽量化同底,再用单调性
例题2:
(2013·课标全国Ⅱ)设a=log36,b=log510,c=log714,则( )
A.c>b>a
B.b>c>a
C.a>c>b
D.a>b>c
答案 D
解析

显然a>b>c.
础方法3:指数,对数比较大小,找中介值进行比较

A.x<y<z
B.z<x<y
C.z<y<x
D.y<z<x
答案 D
解析 ∵x=lnπ>ln e,∴x>1.


综上可得,y<z<x
基础方法4:底数不同,指数相同,则构造幂函数
例题4:设a=0.50.5,b=0.30.5,c=log0.30.2,则a,b,c的大小关系是( )
A.a>b>c
B.a<b<c
C.b<a<c
D.a<c<b
解析 (1)根据幂函数y=x0.5的单调性,可得0.30.5<0.50.5<10.5=1,即b<a<1;
根据对数函数y=log0.3x的单调性,可得log0.30.2>log0.30.3=1,即c>1.
所以b<a<c.
基础方法 5:利用同底数、同指数或同真数等借助于函数单调性或图象求解
例题5:已知a=5log23.4,b=5log43.6,c=(1/5)log30.3( )
A.a>b>c
B.b>a>c
C.a>c>b
D.c>a>b
解析:方法一 在同一坐标系中
分别作出函数y=log2x,y=log3x,y=log4x的图象,如图所示.

由图象知:
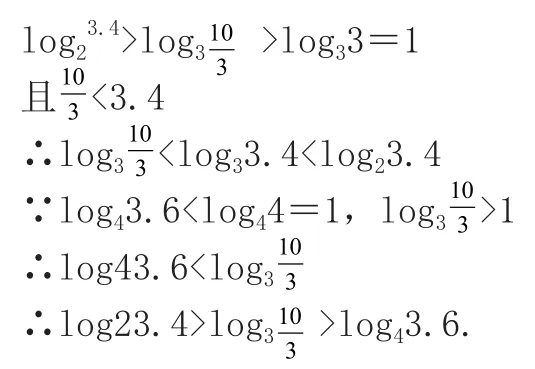
由于为y=5x增函数,5log23.4>(1/5)log30.3>5log43.6, 即5log23.4>(1/5)log30.3>5log43.6
基础方法6:函数奇偶性及指数式、对数式的运算.
例题6:(2015·天津理,7)已知定义在R上的函数f(x)=2|x-m|-1(m为实数)为偶函数.记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
A.a<b<c
B.a<c<b
C.c<a<b
D.c<b<a
[答案] C
[解析] 考查函数奇偶性及指数式、对数式的运算.
因为函数f(x)=2|x-m|-1为偶函数,所以m=0,
即f(x)=2|x|-1,所以

所以c<a<b,故选C.
总之,比较几个数(幂或对数)的大小是指数函数、对数函数和幂函数性质的重要应用,在具体解题过程中,应先观察要比较的数的特征再选用合适的方法比较大小,有时需要先结合幂与对数的运算性质对要比较的数进行合理的变形,再进行大小比较。
