如何提升数学学习力
2017-06-20上海市格致中学俞志钢
上海市格致中学 俞志钢
一、问题背景
伟大的数学家华罗庚曾经说过:“数学是壮丽多彩,千姿百态,引人入胜的”,然而数学的学习却可能会令同学感到畏惧。与初中相比,高中数学的知识面更广、深度更深,运用更为灵活。学生会普遍感到课堂教学内容太多、节奏太快,知识掌握不够牢固,不能“活”用等。于是,如何提高和培养高中生数学学习力成为普通高中教师面临的重要而艰巨的课题。
刚才提及的一个词“学习力”正是眼下时髦的一个词,百度一下,有关学习力的解释很多,我个人还是比较认同:学习力就是能够帮助一个人更快、更好地学习一切的能力。学习力的构成,包括:学习动力、学习态度、学习毅力、学习方法、学习效率、创新思维和创造能力等要素。
二、数学学习力的几点思考
(一)学习动力、态度
特级教师王连笑曾说过:数学不等于数学题,更不仅仅是解题技巧,数学是一种文化。数学不仅是计算、解题,数学中还包括学科思想文化、科学的思维方式以及人生哲理。对于学生来说,这些比数学知识本身更为重要。
新课程告诉我们:要让学生逐步体会数学和日常生活的紧密联系,感知数学是有趣和实用的,逐步了解数学的价值。新教材中的很多实例都很贴近生活,利用教材,让每个学生学会欣赏数学之美,感受数学带来的快乐。在教学中注重采用各种方式,努力激发学生对数学发生兴趣。唯有兴趣,才能有积极持久的学习动力,从而形成良好的学习态度。
(二)学习毅力
学习毅力是指学生自觉地确定学习目标,有意识地控制和调节自己的学习行为,克服困难,以实现预定学习目标的心理过程。顽强的学习毅力不但能促进智力的发展,而且有利于培养学生的创新人格和创造能力。因此,始终围绕学习目标,加强意志力、持续力、战斗力、乐观进取精神的培养,形成良好的学习毅力,才能克服困难,深入持久的进行认知活动,从而有效地获取数学知识,促进智力、能力的发展。
(三)学习方法、效率
达尔文有一句格言:“最有价值的知识是关于方法的知识。”数学成绩的提高离不开好的学习方法。教师要指导学生首先学会听、读;然后学会思考;在数学学习中对数学信息进行比较、联想、抽象 、概括、分析、综合、归纳、演绎、假设、推理等思维活动都是思考。最后,还要学会抓好学习环节,这样学习效率可以大大提高。
三、课堂教学中对于如何提升数学学习力的几点探究
以上几个要素在老师的指导下如果能够内化为良好的学习习惯对于提升学生的数学学习力一定会有帮助!当然,对于提升学生的数学学习力,教师最需要做的还是抓好课堂教学。
事实上,数学是一门思维的科学,思维能力是数学学科能力的核心。数学思维能力是以数学知识为素材,通过空间想象、直觉猜想、归纳抽象、符号表示、运算求解、演绎证明和模式构建等诸方面,对客观事物中的空间形式、数量关系和数学模式进行思考和判断,形成和发展理性思维,构成数学能力的主体。所以数学教学需要始终围绕对学生思维能力的培养进行。
(一)引导学生学会联想 培养思维的创造性
爱因斯坦:“想象力比知识更重要,因为知识是有限的,而想象力概括着世界上的一切,推动着进步,并且是知识进化的源泉.”
数学的运动能量不是推理而是想象。在数学问题的探索中,为了寻求一般规律,教师可以引导学生先考察一些特例,进行归纳,形成猜想,然后再去证明这些猜想正确与否。
(二)渗透数学思想方法 培养思维的综合性
数学问题千变万化,不少学生在题海里疲于奔命却难以奏效,往往“一听就懂”、“一看就会”、“一做就错”。究其原因还是思维的综合能力欠缺。而掌握基本数学思想方法能使数学更易理解、记忆和应用。在教学中,教师要将这些思想和方法渗透给学生,提高学生思维的的综合能力。
(三)进行多种形式的训练,培养思维的发散性
传统的教学比较注重集中思维的训练,而相对忽视了发散思维的培养。发散思维是理解教材、灵活运用知识所必须的,也是迎接信息时代、适应未来生活所必须具备的能力。“一题多解”、“一题多变”是训练发散思维的有效途径。
1.在一题多解中培养思维的广阔性
数学的思维训练通常是以解题教学为中心展开的。在解题中引导学生多角度、多方向的去思考问题,揭示沟通内在联系的纽带,有助于培养思维的广阔性。
2.在一题多变中培养思维的深刻性
①类比变换
正如波利亚说的:“类比是伟大的引路人”,这种借它山之石用以攻玉的思维方法不仅可以提高学生的解题能力,而且可以培养学生思维的深刻性 。如上海新教材高中一年级第二学期P74例9
上海的金茂大厦是改革开放以来的上海超高层标志建筑.有一位建筑爱好者在于金茂大厦底部同一水平线上B的处测得金茂大厦顶部A的仰角为15.660,再向金茂大厦前进500米到达C处,测得金茂大厦顶部A的仰角为22.810.他能否算出金茂大厦的高度?若能算出,请计算其高度(精确到1米)
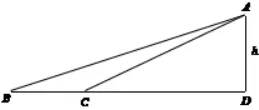
根据题意,作出如下示意图,这样问题转化为求ΔABC的底边BC上的高h。
下面我把题目变换为 如图:从气球A上测得正前方的河流的两岸B,C的俯角分别为α,β,如果这时气球的高度是h,求河流的宽度BC。
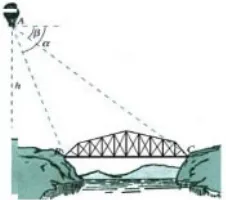
这样一来,原来的仰角变为俯角,原来是已知BC的长度,求高度h.现在已知高度,反过来求河流BC的宽度。这里做了一个方法上的类比变换。
②逆向变换
所谓逆向变换是指将已知条件和未知条件进行转换,或将一些数学概念、定理、公式进行逆向应用。
③拓展变换
如上海新教材P39高一第一学期(上海教育出版社)例1解不等式
拓展变换: 已知a∈R,解不等式
总之,数学教学与思维密切相关,数学教学既是学生知识积累的过程,也是学生思维得到发展的过程。灵活多变的教学是培养学生思维能力的有效途径。教师需要在三类课程的教学中进行有机的整合,深入研究数学活动和数学思维特点,寻求数学活的规律,通过激发思维能力可以促进学习力的提升。
最后我想说的是:学习力是可贵的生命力、是活跃的创造力、是一种最本质的竞争力,值得我们去探究!
