基于振幅和频率的砂体厚度校正新方法及其应用
——以渤海南部X油田为例
2017-06-19薛明星刘传奇陈文雄
薛明星,刘传奇,高 磊,陈文雄,刘 欢
(中海石油(中国)有限公司天津分公司渤海石油研究院,天津塘沽 300452)
基于振幅和频率的砂体厚度校正新方法及其应用
——以渤海南部X油田为例
薛明星,刘传奇,高 磊,陈文雄,刘 欢
(中海石油(中国)有限公司天津分公司渤海石油研究院,天津塘沽 300452)
传统的砂体厚度图校正方法基于砂体顶底反射视时间厚度,然而该属性仅在砂体厚度大于1/4波长时与真厚度近似具有线性关系,当砂体厚度小于1/4波长时将产生较大的校正误差。基于楔状模型正演,使用反射振幅与中心频率构建了一种在3/7波长范围内与砂体真厚度具有线性关系的新属性 ,给出了一种全新的砂体厚度校正方法。新方法思路简洁,易于实现,适用于生产中大多数横向较均匀砂体的厚度校正问题。应用实例表明,新方法校正结果精确合理,显著优于传统方法。
砂体厚度校正;视厚度;反射振幅;中心频率
在河流相油田开发过程中,沉积砂体厚度的计算精度直接影响油田储量的确定以及开发井井位的优化。传统的砂体厚度校正方法基于视厚度进行计算,假定其与真厚度具有线性关系,视厚度能够反映真厚度的变化趋势,然而众所周知,该关系只在砂体厚度大于1/4波长的条件下近似成立,当砂体厚度小于1/4波长时,视厚度基本保持不变,此时不能反映真厚度的变化趋势[1-5]。
油田实际开发过程中涉及大量整体或局部为薄层的含油砂体,对于此类情况传统方法必然产生较大误差,在无井钻遇处得到的砂体厚度可能与实际厚度相去甚远。合理的校正方法要求校正的属性应该与砂体真厚度在较宽的厚度范围内具有简单的线性关系。研究表明,可以利用振幅与频率构造具有这一特征的属性。本文利用雷克子波合成记录,给出了联合利用砂体反射振幅与中心频率进行厚度校正的新思路[6-9]。
1 基本原理[7-13]
为了探讨与真厚度具有线性关系的新属性,采用雷克子波合成地震记录,考虑如图1a所示顶底反射系数等幅异号楔状砂体模型,利用褶积关系得到合成地震记录(图1b,波速2 300 m/s,子波主频40 Hz),由图1可提取楔状模型振幅与时间厚度曲线(图2),振幅在14.4 m(1/4波长)处发生调谐。传统砂体厚度校正方法利用各井点实钻厚度值对砂体视厚度进行校正得到最终校正结果,然而图2表明,当砂体厚度小于1/4波长时,视厚度不能反映真厚度的变化趋势。中心频率与时域提取的振幅属性关系如图3。
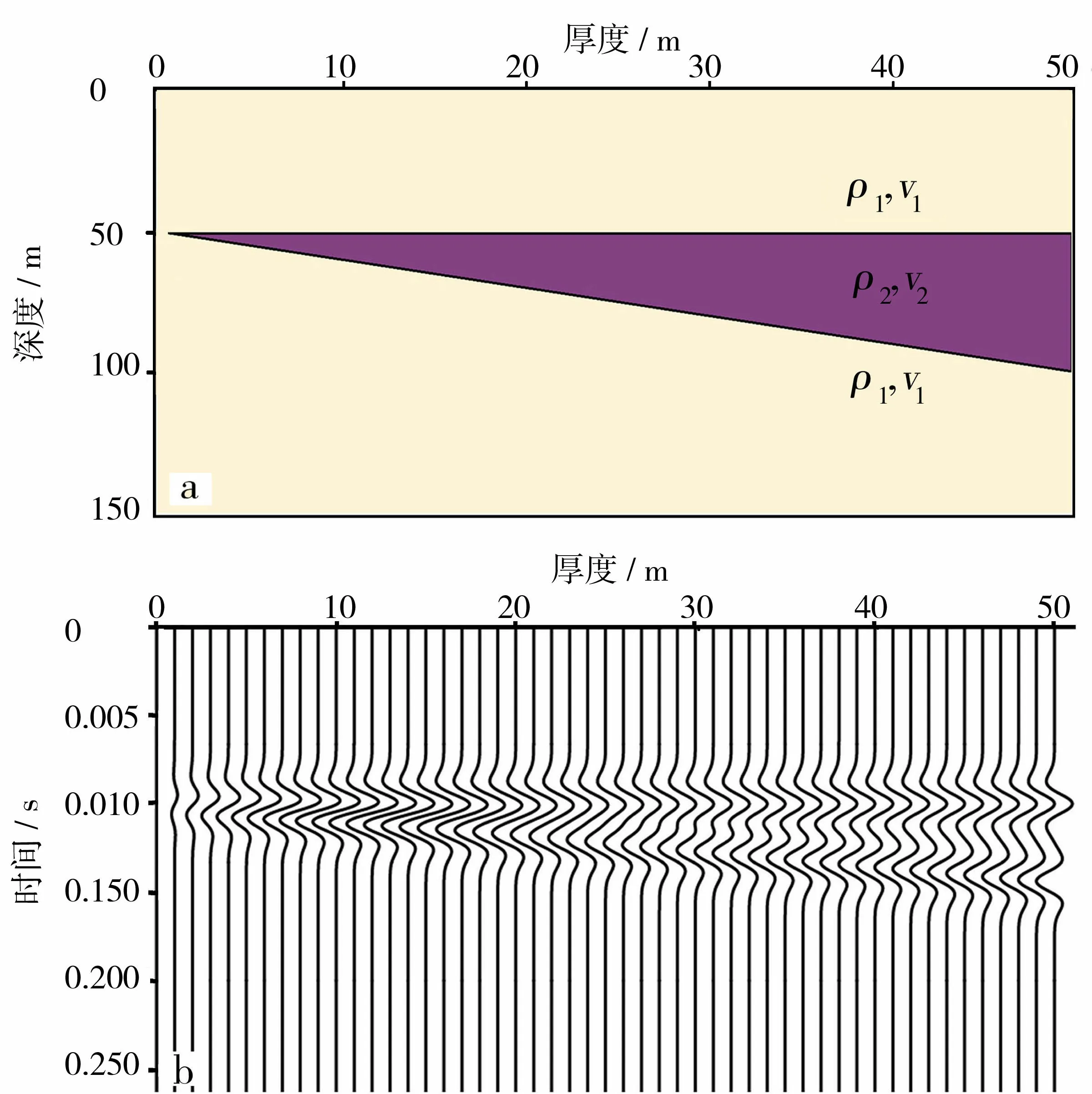
图1 楔状模型(a)及其合成地震记录(b)
由图3可知,楔状模型反射振幅曲线随厚度的增加具有一个极大值点,即1/4波长调谐点,而频率曲线具有一个极小值点。当厚度小于1/4波长时,振幅与厚度近似具有线性关系,频率变化则较为缓慢;当厚度大于1/4波长且小于频率极值点时,振幅下降,同时频率值也快速降低。因此,可尝试利用频率曲线的特点对振幅曲线进行改造,使新曲线在比1/4波长更宽的范围内与厚度具有线性关系。最直接的改造形式为采用A/F与厚度的关系曲线(A为振幅,F为频率),曲线形态如图4所示,由该图可知,曲线极值已经向右移动,对应厚度超过1/4波长,但移动量较小且极值点左侧曲线线性特征不理想,为此可将变换式修正为A/Fn,加强频率对曲线的调整作用。图5为n分别取3,3.5,4时变换式A/Fn的形态。经过反复尝试,最终确定当n取3.5时,新曲线极值点左侧部分与厚度的线性关系最理想,且极值点对应厚度值约为3/7波长(图5实例中极值点厚度为25 m,3/7波长为24.6 m)。由于单砂体储层研究以波阻抗反演或90°相移方法为基础,而一般这两种方法所能刻画砂体的厚度大多小于3/7波长,因此采用变换式表达的新属性对砂体厚度进行校正,能够满足大多数生产实际的需要。新的厚度校正方法需要提取砂体顶面(或底面)反射振幅及中心频率计算新属性 ,再利用各井点实钻砂体厚度值对该属性进行校正,即获得厚度最终校正结果。

图2 楔状模型振幅、时间与厚度关系
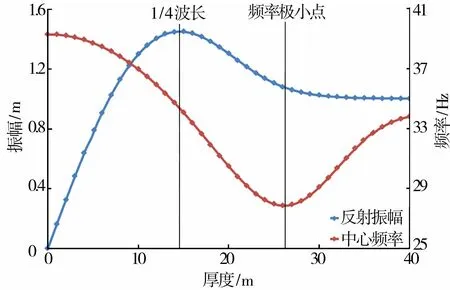
图3 楔状模型振幅、中心频率与厚度关系

图4 楔状模型振幅、中心频率与厚度关系

图5 n取不同值时A/Fn极大值点左侧曲线形态
2 应用实例
以渤海南油X油田F25-1575砂体为例,该含油砂体所在层段1/4波长为14 m,砂体先后被F25、F21两口井钻遇(图6)。两口井处砂体时间厚度均为12 ms,F25井实钻厚度9.2 m,按照传统厚度校正方法预测,F21井处砂体厚度也应为9.2 m,但实钻表明F21井处砂体厚度仅为5.6 m。考虑振幅频率信息,F25井及F21井处的振幅分别为-30 446 dB与-21 262 dB,中心频率分别为33 Hz与34 Hz,按照新方法计算A/F3.5,分别为0.147 5与0.092 8,由此预测F21井处砂体厚度为5.8 m,与实钻结果十分接近。根据实钻信息采用传统方法对砂体厚度进行校正如图7a,将其与砂体剖面图(图6)对比发现,剖面上砂体最左端高部位(区域A)时间厚度达20毫秒,但校正结果厚度仅为8~9 m,显然不合理,这是受F21井处较薄的实钻厚度影响的结果。利用振幅频率信息采用新方法对砂体厚度进行校正,如图7b,此时砂体左端高部位校正结果可达12~14 m,该厚度与砂体地震反射特征更协调,计算结果准确合理。

图6 F25-1575砂体过井90度相移资料剖面

图7 F25-1575砂体90度相移振幅属性与厚度等值线叠合
3 结论
为了克服基于顶底反射视厚度进行砂体厚度校正的传统方法存在的缺陷,本文通过反射振幅和中心频率构造了一种在3/7波长范围内与砂体真厚度具有线性关系的新属性 ,并给出了一种全新的砂体厚度校正方法,该方法简洁、易于实现。应用实例表明,当薄层存在时,新方法校正结果更加精确,显著优于传统方法,值得推广应用。当然,新属性的构建基于均匀的楔状体模型,要求砂体横向较均匀、物性变化小,这是该方法使用过程中应该注意的地方。对于横向物性变化较大的砂体厚度的校正问题,还需要开展进一步的研究工作。
[1] 孙鲁平,郑晓东,首皓,等.薄层地震峰值频率与厚度关系研究[J].石油地球物理勘探,2010,45(2):254-259.
[2] 王云专,郭雪豹,邢小林,等.薄层峰值频率特征分析[J].地球物理学进展,2013,28(5):2515-2523.
[3] 张海燕,李庆忠.几种常用解析子波的特性分析[J].石油地球物理勘探,2007,42(6):651-657.
[4] 李雪英,李东庆,白诗缘.薄层研究方法综述[J].地球物理学进展,2014,29(5):2197-2203.
[5] 黄真萍,王晓华,王云专.薄层地震属性参数分析和厚度预测[J].石油物探,1997,36(3):28-38.
[6] 汪恩华,贺振华,李庆忠.薄储层厚度计算新方法探索[J].物探化探计算技术,2001,23(1):22-25.
[7] 宁松华,汪勇.基于振幅属性分析法的楔状砂体厚度预测研究[J].石油天然气学报,2010,32(5):90-94.
[8] 云美厚,丁伟.地震子波频率浅析[J].石油物探,2005,44(6):578-581.
[9] 张兆辉,李胜军,张忠义,等.目标砂体厚度精细预测技术在歧南地区的应用[J].地球物理学进展,2014,29(5):2314-2319.
[10] 袁子龙,杨冰,王建国.薄层、薄互层地震反射时间域与频率域正演模拟研究及应用[J].石油物探,1996,35(3):14-20.
[11] 邹华胜,宁书年,杨峰,等.支持向量机在储层厚度预测和计算中的应用[J].地球物理学进展,2007,22(5):1597-1601.
[12] 王云专,王晓华,黄真萍.时域频域多参数薄层厚度预测[J].大庆石油学院学报,1996,20(3):16-20.
[13] 李雪英,陈树民,王建民,等。薄层时频特征的正演模拟[J].地球物理学报,2012,55(10):3410-3419.
编辑:赵川喜
1673-8217(2017)03-0070-03
2016-10-19
薛明星,工程师,1983年出生,2008年毕业于成都理工大学物探专业,现从事油田开发地震研究工作。
TE112
A
