基于议价模型的航空联盟动态转让价格研究

顾颖菁，朱金福

（南京航空航天大学民航学院，江苏 南京 211106）

基于议价模型的航空联盟动态转让价格研究

顾颖菁，朱金福

（南京航空航天大学民航学院，江苏 南京 211106）

随着全球经济一体化的发展，航空联盟的不断加深，航空联盟成员如何合理地分配收益已经成为航空公司研究的重要问题。用讨价还价动态博弈法研究了航空联盟中市场航空公司与承运航空公司在完全信息与非完全信息下的转让价格问题，并建立了非完全信息下按比例分配多阶段议价模型。研究结果表明：讨价还价博弈下的转移价格能够激励航空公司的销售，市场航空公司在不完全信息情况下，会获得较高收益；承运航空公司在非完全信息下，会获得较高收益。非完全信息下按比例分配多阶段议价模型弥补了现有分配方式不足，既保证有利于航空联盟的票不被拒绝，也确保航空公司的利益不会减少。

航空联盟；转移价格；动态博弈；议价模型

航空公司即使在加入航空联盟后，他们的最终目的还是自身利益最大化，Boyd[1]和Wright等[2]提出航空联盟会在航线运营前制定收益分配协议（SPAs），该协议规定了收益分配是以怎样的方式进行收益分配，主要有以下两种方式：

1）按比例分配支付：根据航空联盟协议，市场航空公司收到一个旅客请求，票价为，根据比例分配确保自己航段可售，将剩余票价给承运航空公司，承运航空公司确认可行，出售，确认不可行，拒绝。这种分配方式是目前航空联盟里使用最多的方式，但可能会导致增加航空联盟收益的票被拒绝，例如：航空公司1承运A—B航段，票价苊525，航空公司2承运B—C航段，票价苊1530，对于A—C段的票，分配比例为20%和80%。当航空公司1接收到一个旅客请求，价值苊2 250，对于整个联盟，苊2 250>苊525+苊1 530，应出售，对于航空公司1，苊2 250×20%=苊450<苊525，所以拒绝。

2）支付转让价格：根据合作协议，市场航空公司在使用承运航空公司舱位时，支付给承运航空公司转让价格。Vinod[3]提出了影子价格为动态的转让价格，影子价格以承运航空公司的期望收益，但该分配方式对承运航空公司不利；Graf等[4]提出的基于期权方式，即市场航空公司通过预先支付期权价格给承运航空公司，保留一定数量的舱位，若使用则支付剩余价格，如不使用，期权价格将不退还；Cetiner等[5]提出用合作博弈论的方法研究航空联盟的收益共享机制，通过计算“核”来评价现有分配机制的公平性，并且分析了相较于集中控制，非集中情况下收益分配是否受到了影响以及影响了多少，研究得出，基于航段自身价值的分配方式优于其它方式。

在航空联盟收益管理中，收益分配与舱位控制相辅相成，De la Torr[6]讨论了代码共享下的舱位分配方法，一种是由运营商控制固定或非固定舱位数，这种区域空间代码共享并没有得到广泛使用，另一种是自由销售协议，也是目前最常用的，他还提出了由于高估代码共享航线可能造成潜在损失，可以通过按比例分配收益来避免个体损失；Topaloglu[7]针对多航段联盟网络的舱位控制问题，在多航段联盟网络中，假设航空公司独立地进行舱位容量控制的决策，只有出售机票的航空公司才能决定接受或拒绝旅客到达请求，建立了单一航空公司的舱位控制线性规划模型，通过对偶方法得到航空公司的收益分配份额；Waldemar等[8]用纳什均衡方法研究了平行联盟和互补联盟内的竞争模型，第一次在模型中考虑了多等级舱位。

目前确定转让价格多少在于航空联盟协议或者市场航空公司报价，承运航空公司只能被动的接受或者拒绝，没有再次议价的机会。本文使用了讨价还价博弈方法，讨价还价模型是一个完全信息动态博弈模型，通过共同收益，机会收益，以及对差值可接受的委曲程度共同作用于决策过程，是双方共同作用的结果，通过讨价还价博弈方法确定支付价格，可以最大程度上保证收益分配的公平性。在研究中，还涉及到EMSR方法，Peter[9]在他的博士论文中发展了Littlewood[10]的方法并给出严格的证明，该方法引起了许多后续研究，也在很多领域都得到应用。张秀敏等[11]使用投标价格法，在铁路客运领域提出改进方法：隐藏价格（EMSR）法，对各区段座位实行嵌套结构管理。

蒋菱等[12]建立不完全信息条件下的讨价还价模型，用逆袭归纳法解出了模型的理论均衡解，并得到了实验均衡解，结果表明实验均衡解达不到理论均衡解，并得出在不完全信息下，报价顺序的先后决定了参与方分配利益的多少；詹文杰等[13]研究了有限理性假设下“多对多”讨价还价的策略，建立“双种群”复制动态模型，证明了只有严格纳什均衡才能成为“多对多”讨价还价的演化稳定策略；杜少甫等[14]用Nash讨价还价博弈方法建立了供应链效用的公平关切框架，构建了描述性的行为运筹模型，探讨零售商的公平关切程度如何影响供应链成员的决策；简惠云等[15]分析与比较风险规避型供应链分别采取Stackelberg博弈和Nash讨价还价博弈时的最优化决策，探讨供应链主导方如何根据合作伙伴的风险规避水平选择契约和博弈机制。

1 完全信息下的讨价还价模型

互补型航空联盟，即在一条航线上，成员航空公司分别承运不同的航段。市场航空公司是指在一条共同承运航线上出售机票的航空公司，承运航空公司是指未出售机票，但参与了承运的航空公司。成员航空公司共同运营的航线上都可以出售机票，市场航空公司和承运航空公司并不特指某一方，而是根据出售机票方，相互转换。转让价格是指市场航空公司为使用承运航空公司舱位所支付给承运航空公司的价格，也是收益分配的一种方式。

1.1 条件假设与参数说明

1）完全信息是指市场航空公司和承运航空公司能够了解各自的舱位等级、需求以及当前实际的销售情况。

2）当市场航空公司收到一个票价为p联运旅客的请求时，市场航空公司和承运航空公司单个航段上当前最低期望收益和最高期望收益为［a1，a2］，［b1，b2］，当前最低期望收益为此时的边际收益，可用EMSR方法计算，当前最高期望收益为此航段上的最高票价。市场航空公司接受使用承运航空公司舱位的价格区间为［p-a2，p-a1］，承运航空公司同意承运的价格区间为［b1，b2］（其中p-a1为市场航空公司使用承运航空公司舱位的最高支付价格，b1为承运航空公司同意承运的最低接受价格，并且p-a1≥b1）。

3）令r为谈判成功的最优解，则r∈［b1，p-a1］，其中p-a1－r为市场航空的剩余，r－b1为承运航空的剩余。

4）讨价还价是动态博弈过程，分为若干阶段，由市场航空公司先出价，承运航空公司同意即停止，若不同意，则由承运航空公司出价。

5）谈判过程具有时间价值，随着谈判时间的加长，失去该旅客的几率加大，双方的收益都将有损耗。虽然失去旅客是共同行为，但是双方对于失去该旅客的害怕程度不一样，将害怕程度转设为“客座率”，分别为σ1，σ2（0≤σ1≤1，0≤σ2≤1），σ1，σ2越大，表明“客座率”越高，害怕失去该旅客的程度越低。

1.2 模型建立

在完全信息状态下，将谈判区间［b1，p-a1］投影到［0，1］上，区间［0，1］中的r′为r在相应区间上的映射：r′＝（r－b1）／（p-a1－b1），可以转化为经典鲁宾斯坦的分蛋糕博弈。他的分析思路，是根据最后被接受的报价提出者的不同，为该参与人提出最“合理”的报价，这一报价是根据两人议价能力（即贴现因子）而得出的一次性最优报价值。

当议价阶段不受限制时，得到Nash均衡的结果是

由式（1）可知，由于市场航空公司接受旅客请求，具有先出价权，并且获得的收益大于承运航空公司，该方式可以激励成员航空公司售票；式（2）为具体转让价格。

1.3 完全信息下的舱位转让流程

航空公司1与航空公司2实行联盟内合作，当航空公司1接收到一个票价为p的旅客请求，此时航空公司1为市场航空公司，如果票价小于两家航空公司的最低期望收益之和，市场航空公司直接拒绝该旅客，如果票价大于或等于两家航空公司的最低期望收益之和，市场公司同意接受该旅客，并与航空公司2，也就是承运航空公司进行讨价还价博弈，确定最终转让价格，流程见图1。

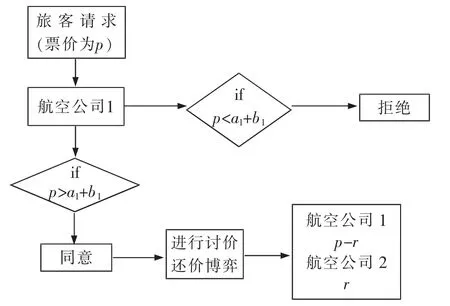
图1 完全信息下的舱位转让流程Fig.1 Capacity transfer process with complete information

2 非完全信息下的讨价还价模型

由于航空联盟涉及到反垄断法，以及技术上的欠缺，成员航空公司之间并不能完全信息共享，市场航空公司和承运航空公司不能知道对方的舱位等级、需求、以及当前的销售数，需要改进完全信息下的讨价还价模型。

2.1 参数说明

1）市场航空公司和承运航空公司可以通过销售网站等途径知道对方目前所开放的舱位等级的票价以及所在折扣。

2）市场航空公司与承运航空公司目前各自航段上开放的舱位等级的票价为a1′和b1′，市场航空公司认为b1′是承运航空最低期望收益，市场航空公司接受的价格区间为［b1′，p-a1］，承运航空公司接受价格区间为［b1，x1］，x1为承运航空公司认为市场航空公司所能承受的最大价格，x1=p-a1′；因此承运航空公司接受价格区间为［b1′，p-a1′］。

3）市场航空公司与承运航空公司当前预期收益为a1，b1，因为票卖出的概率小于1，所以b1′＞b1，a1′＞a1。

4）令ra′为市场航空公司认为谈判成功的最优解，则ra′∈［b1′，p-a1］，rb′为承运航空公司认为谈判成功的最优解，则rb′∈［b1，p-a1′］。

5）对于航空公司双方怕失去旅客的程度，在上文中用客座率表示，在信息不完全的情况下，不知道相互航段当前的客座率，但可以用当前票价所在折扣预估当前的客座率，设为σ1′，σ2′（0≤σ1′≤1，0≤σ2′≤1），σ1′，σ2′越大，则当前票价折扣越高，怕失去该旅客的可能性越低。

2.2 模型建立

在不限次讨价还价模型下，市场航空公司愿意支付给承运航空公司的价格ra′为

承运航空公司愿意接受的价格rb′为

由b1′＞b1，a1′＞a1，可得ra′＞rb′。若市场航空公司先出价ra′，ra′＞rb′，承运航空公司同意转让，此时市场航空公司支付的转让价格高于完全信息下。若承运航空公司先出价rb′，rb′＜ra′，市场航空公司也同意接受转让舱位，此时市场航空公司支付的转让价格低于完全信息下。由于是市场航空公司最后决定该票是否卖出，市场航空有权选择利于自己的方式，让承运航空先出价，那么市场航空公司的收益将高于完全信息下的收益。

3 非完全信息下的多阶段议价模型

在市场航空不告知承运航空票价p为多少，并且互相不知道舱位等级、需求以及当前的销售数，为了能够解决不完全信息下有利于航空联盟收益的票价被拒绝这一问题，建立多阶段议价模型进行讨论，该模型基于航空联盟目前使用最多的按比例分配的基础上，先在联盟协议中确定基础分配比例，再根据多阶段议价模型确定最终转让价格。假设在航空联盟中，博弈双方都诚实守信，因为如果市场航空公司刻意降低转让价格，或承运航空公司刻意抬高转让价格，会使另一方的利益得到损害，并破坏联盟的稳定性，一经发现会收到严重的惩罚。

3.1 议价步骤

实施动态议价的关键，在于两点：一是市场航空公司确保所卖出的座位在联盟网络航线上可行，取决于市场公司所获得的收益；二是承运航空公司是否同意接受市场航空公司旅客，主要取决于市场航空公司支付给承运航空公司的价格。

1）根据在航空联盟协议中，收益分配比例确定为坠，1-坠。当市场航空公司收到一个票价为p联运旅客的请求时，市场航空公司根据收益分配比例以及当前期望收益确定转让价格k1。

2）承运航空公司接收到转让价格k1之后，确定是否接受，若接受，结束；若不接受，向市场航空公司提出新的接受价格k2。

3）市场航空公司确定新提出的价格k2是否接受，若接受，结束；若不接受，向承运航空公司再次提出新的接受价格k3。

4）承运航空公司接收到新的转让价格k3之后，确定是否接受，若接受，结束；若不接受，则拒绝该票，结束。

3.2 模型建立

建立如下议价模型

式（5）中E（R）为航空联盟收益；U为议价结果；u1，u2，u3为议价阶段决策变量，如果同意接受转让价格为1，否则为0。式（6）为市场航空公司确定首次转让价格，确保市场航空公司出售共同航段这张票的收益不比出售单独航段票的收益少。式（7）为议价规则，其中a1，b1为市场航空公司和承运航空公司当前期望收益，保证了承运航空公司的收益也是大于或等于出售单独航段的票。

该议价模型既可以保证有利于航空联盟的票不被拒绝，又可以让市场航空公司和承运航空公司的收益能够大于或等于出售单独航段的收益，使得联盟更加稳定。

4 数据分析

联盟内一家航空公司运用菲尼克斯（PHX）—芝加哥（ORD）的航线（Airline1），另一家航空公司运用芝加哥（ORD）—法兰克（FRA）福航线（Airline2），可用座位分别为250座和200座，根据航空联盟协议，航空公司协定好收益分配比例为40%和60%，航空公司加入航空联盟前与加入航空联盟后对于每个航段的票价和需求分别如表1所示。

根据EMSR方法，计算舱位分配如表2所示。

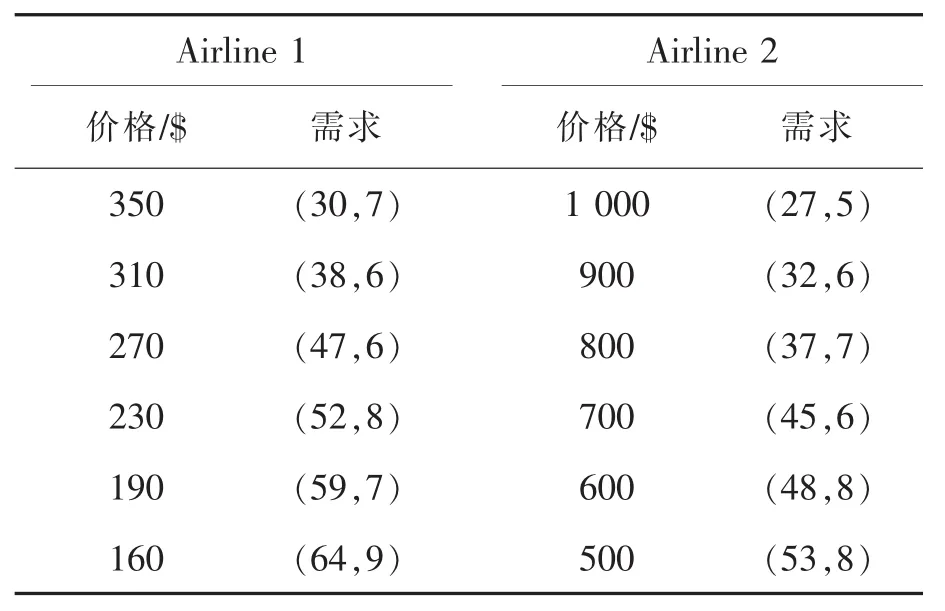
表1 两家航空公司的票价与需求Tab.1 Fares and demands of two airlines’ODF

表2 票价等级和舱位分配Tab.2 Fare class and seat capacity allocation

选取任意5组销售舱位组合下，市场航空公司的票价和期望收益见表3。

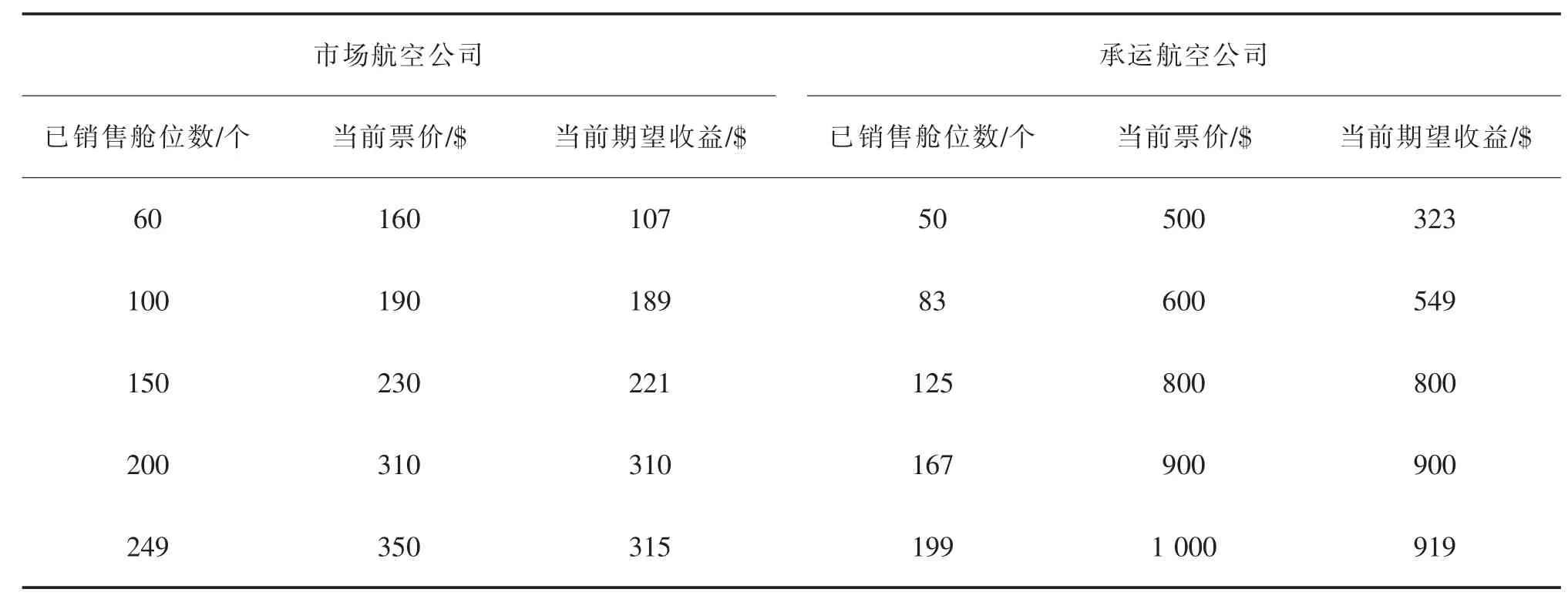
表3 已售舱位数及当前期望收益Tab.3 Capacity seat sold and expected revenue

根据公式分别计算出完全信息和非完全信息下的转让价格见表4和表5。

表4 完全信息讨价还价下的转让价格Tab.4 Transfer price under complete information bargaining $

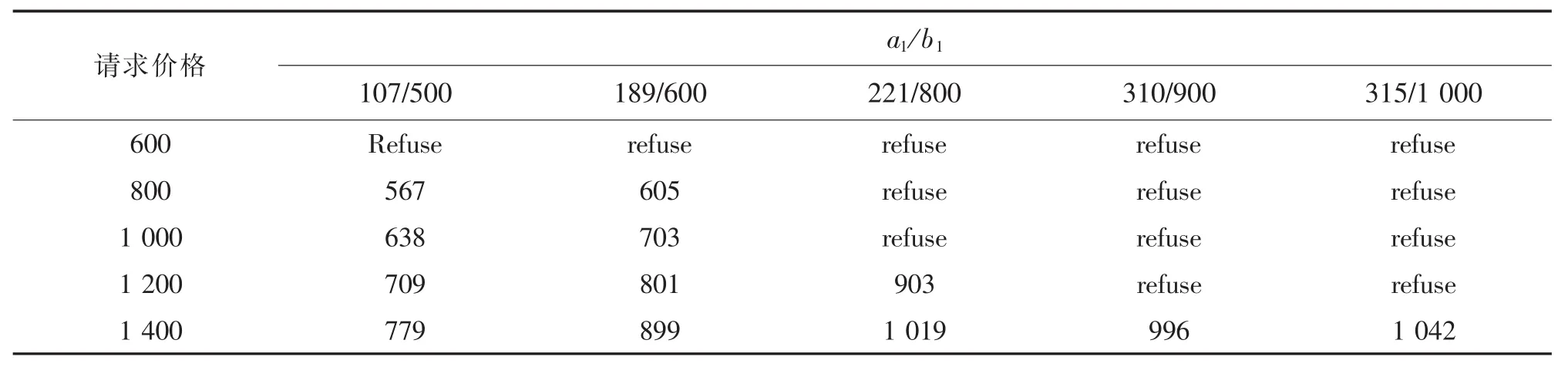
表5 非完全信息讨价还价下市场航空公司先出价的转让价格Tab.5 Transfer price of the marketing airline under incomplete information bargaining $

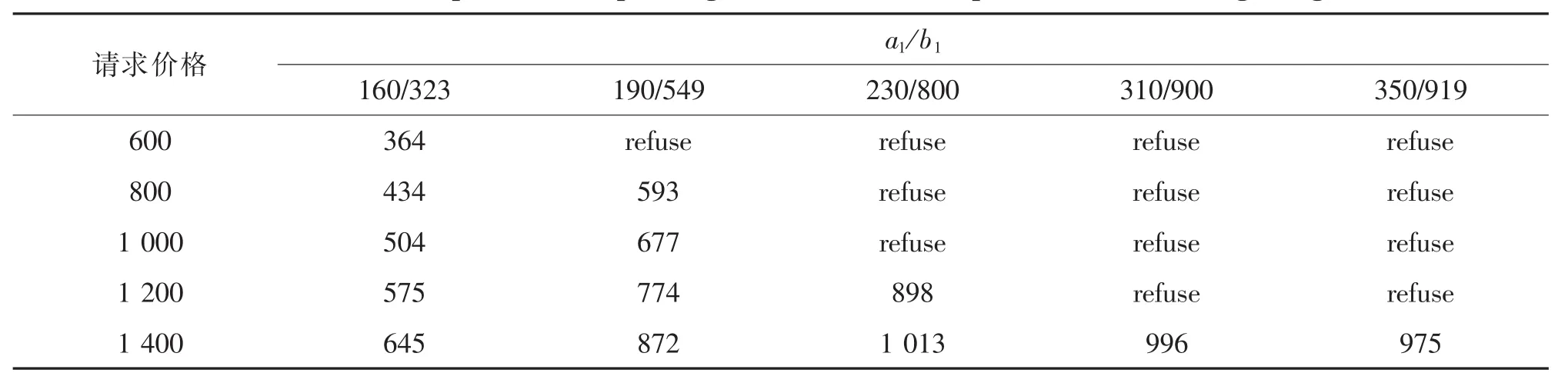
表6 非完全信息讨价还价下承运航空公司先出价的转让价格Tab.6 Transfer price of the operating airline under incomplete information bargaining $

根据计算结果分析：在完全信息讨价还价情况下，承运航空公司所获得的转让价格最低，市场航空公司的收益比例最高；在非完全信息讨价还价下，承运航空公司先出价，承运航空公司得到的转让价格较低，市场航空公司所得到的收益比例较高。可以说明在信息未知的情况下，市场航空公司由于不知道承运航空公司的情况，愿意出更高的转让价格“购买”承运航空公司的座位。对于承运航空公司来说，并不是知道的信息越多越好，在非完全信息下所获得的转让价格反而更高。但是在非完全信息讨价还价情况下，对于航空联盟有利的票可能会被拒绝。见表7和表8。

表7 按比例分配收益Tab.7 Revenue sharing in proportion $

表8 非完全信息下多阶段议价结果Tab.8 Revenue sharing of multi-stage bargaining under incomplete information $

比较表7和表8可以得出，多阶段议价模型可以保证在非完全信息下，对航空联盟有利的票不被拒绝，这改进了当前使用最广泛的按比例分配方法，因为无论按照什么方法计算出的精确比例，都会存在这个问题。

5 结论

本文使用讨价还价动态博弈模型，研究了完全信息下和非完全信息下市场航空公司所支付的转让价格，在完全信息下，所有对航空联盟有利的票都会被接受，在非完全信息下，使用讨价还价模型，会因为信息的不完全导致一部分对航空联盟有利的票被拒绝。用讨价还价方法得到的转让价格，是双方博弈的结果，由于市场航空公司是机票销售方具有最终决定权，因此在相同条件下对于增加部分收益分到的比例高于承运航空公司，除此之外，转让价格也跟航空公司的客座率相关，客座率越高，分到的比例越高，这可以激励航空公司销售。

建立的多阶段议价模型，是基于航空公司目前使用最多的按比例收益分配的方式之上。在不违反反垄断法的前期下，弥补了目前分配方式的缺陷，结果表明，多阶段议价模型可以防止有利于航空联盟的票被拒绝，并且保证各航空公司的利益不低于出售单航段票。

[1]BOYD A.Airline alliance revenue management：Global alliances within the airline industry add complexity to the yield management problem[J].OR MS Today，1988，25：28-31.

[2]WRIGHT C P.Dynamic revenue management in airline alliance[J].Transportation Science，2010：15-37.

[3]VINOD B.Alliance revenue management：Journal of revenue and pricing[J].Management Science，2005，4（1）：66-82.

[4]GRAF M，KIMMS A.Transfer price optimization for option-based airline alliance revenue management[J].International Journal of Production Economics，2013，9：281－293.

[5]QETINER D，KIMMS A.Assessing fairness of selfish revenue sharing mechanisms for airline alliances[J].Omega，2013，8：641－652.

[6]DE LA TORRE P E.Airline alliance：The airline perspective[R].London：Cambridge，Massachusetts Institute of Technology，Dept of Aeronautics and Astronautics，Flight Transportation Laboratory，1999：45－62.

[7]TOPALOGLU H.A duality based approach for network revenue management in airline alliances[J].Journal of Revenue&Pricing Management，2012，11（5）：500－517.

[8]WALDEMAR G，KIMMS A.Revenue management under horizontal and vertical competition within airline alliances[J].Omega，2015，6：1－28.

[9]PETER P B.Air travel demand and airline seat inventory management[D].Cam bridge：Massachusetts Institute of Technology，1987.

[10]LITTLEWOOD K.Forecasting and Control of Passenger Bookings[R].Israel：AGIFORS Symposium，1972：21-34.

[11]张秀敏，文曙东.基于投标价格法的铁路客运收益管理方法改进[J].华东交通大学学报，2005，22（3）：63-66.

[12]蒋菱，王峥，黄仁乐，等.基于不完全信息下讨价还价模型的动态联盟利益分配研究[J].价值工程，2016（17）：231－234.

[13]詹文杰，邹轶.基于演化博弈的讨价还价策略研究[J].系统工程理论与实践，2014（5）：1181－1187.

[14]杜少甫，朱贾昂，高冬，等.Nash讨价还价公平参考下的供应链优化决策[J].管理科学学报，2013（3）：68-72.

[15]简惠云，许民利.风险规避下基于Stackelberg博弈与Nash讨价还价博弈的供应链契约比较[J].管理学报，2016（3）：447-453.

Research on Transfer Price of Airline Alliance Based on Bargaining Model

Gu Yingjing，Zhu Jinfu
（College of Civil Aviation，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

With the development of global economic integration and the deepening of aviation alliance,a major issue that needs to be addressed is how to share the revenue generated from selling tickets for products among the individual airlines.Through the theory of bargaining dynamic game,this paper analyzed the transfer price between marketing airline and operating airline with complete and incomplete information and established the multi-stage bargaining model of proportional distribution with incomplete information.The results showed that the transfer price based on bargaining game can encourage airlines to sell tickets,and marketing airlines yield high revenues with incomplete information.Conversely,operating airlines get higher transfer price with incomplete information than that of complete information.This model remedies the limitation of the existing distributive pattern,which may guarantee the enterprises’interest.

airline alliance;transfer price;dynamic game;bargaining model

F562

A

1005-0523（2017）03-0053-07

（责任编辑 姜红贵）

2016－12－06

江苏省博士生科研创新基金（KYLX_0292）

顾颖菁（1988—），女，博士研究生，研究方向航空联盟收益管理。

朱金福（1953—），男，教授，博士生导师，研究方向为航空运输最优化，不正常航班恢复。