基于ISM-Fuzzy AHP模型的轨道交通与常规公交衔接优化研究
2017-06-19刘欣萌
刘欣萌
(西安航空学院经济管理学院,陕西 西安 710077)
基于ISM-Fuzzy AHP模型的轨道交通与常规公交衔接优化研究
刘欣萌
(西安航空学院经济管理学院,陕西 西安 710077)
实现城市轨道交通与常规公交系统协调衔接,建设一体化公共交通,是提高公共交通服务水平的迫切需要,是公共交通系统优先发展战略的内在要求。本文分析了城市轨道交通发展在公交系统中的作用,用解析结构模型建立轨道交通与常规公交接驳影响因素的多级递阶结构,采用模糊层次分析法确定各级因素权重向量,将定性与定量分析相结合对轨道交通与常规公交的衔接优化进行研究,最后以西安地铁3号线为例对本文方法进行实例分析。
城市轨道交通;公共交通系统;接驳;解析结构模型;模糊层次分析法
城市公共交通系统包括城市常规公共交通和城市轨道交通。要真正提高整体运输效率和服务水平,关键之处不仅体现在需要城市交通线路成网、成规模,而且需要系统内的衔接顺畅,换乘方便,达到时间和空间上衔接的融合[1]。因此,城市常规公共交通和城市轨道交通的一体化研究,是城市一体化研究的重要环节[2]。林世生[3]对城市轨道交通与常规公交的衔接进行了初步研究,认为公共汽车与轨道交通的衔接,需要在公共汽车的进入路线、停靠站台、换乘站内的行车路线以及车辆的班次等方面予以重视。谢玉洁,韩宝明,许惠花[4]探讨了基于城市轨道交通的地面常规公共交通线路布局、城市轨道交通与地面常规公交客运一体化的换乘布局、无缝换乘和票制协调问题。
Huo Yue等从交通功能、效益、建设实施的可行性、城市协调性4个角度,提出城市轨道交通线网规划方案综合评价方法[5]。Shi Jingjing,Xue Yunxia指出,利用传统的DEA模型和层次分析法,或者将二者简单结合,在评价效果上会有所欠缺,故提出了一种基于三角模糊AHP和DEA超效率结合的系统评价方法[6]。
综上所述,首先对轨道交通和常规公交衔接问题及其影响因素进行分析,用三角模糊数形式给出互补判断矩阵排序,计算各层次指标权重。根据分析结果提出相应的优化调整措施,从而有效实现二者的接驳,提高居民出行的快捷性和可达性。
1 轨道交通与常规公交衔接制约因素研究
轨道交通与常规公交接驳是一个复杂的系统问题,受到多重因素的制约,应用解析结构模型能够将这些因素之间关系变得明确,层层推进,找出制约轨道交通与常规公交衔接的根本原因,以便解决二者的接驳难题,有助于理解整个公共交通系统的发展趋势,为今后的城市交通整体规划奠定基础。解析结构模型(interpretative structural model,ISM)是用于分析和揭示复杂关系结构的有效方法,它可将系统中各要素之间的复杂、零乱关系分解成清晰的多级递阶结构形式[7],便于找到最直接最根本的影响因素。本文所采用的解析结构模型求解步骤如图1所示。

图1 解析结构模型求解步骤Fig.1 Solution procedure for the interpretative structure model
1.1 确定制约因素
本文列举了制约二者衔接的详细因素,并据此建立解析结构模型,对因素之间的相互关系进行分析。制约因素根据实际情况以及参考文献[8-10]整理得出,如表1所示。

表1 制约轨道交通与常规公交衔接的详细因素Tab.1 Factors restricting the combination of urban rail and bus
1.2 建立邻接矩阵求解可达矩阵
根据表1分析制约因素的直接关系,建立邻接矩阵,由邻接矩阵可以得到可达矩阵,可达矩阵用来表示各因素之间,通过一定的路径可以到达的程度。在可达矩阵求出的基础上,首先确定以下可达集合、先行集合和共同集合,用符号R(si),A(si),C(si)表示,结果如表2所示。
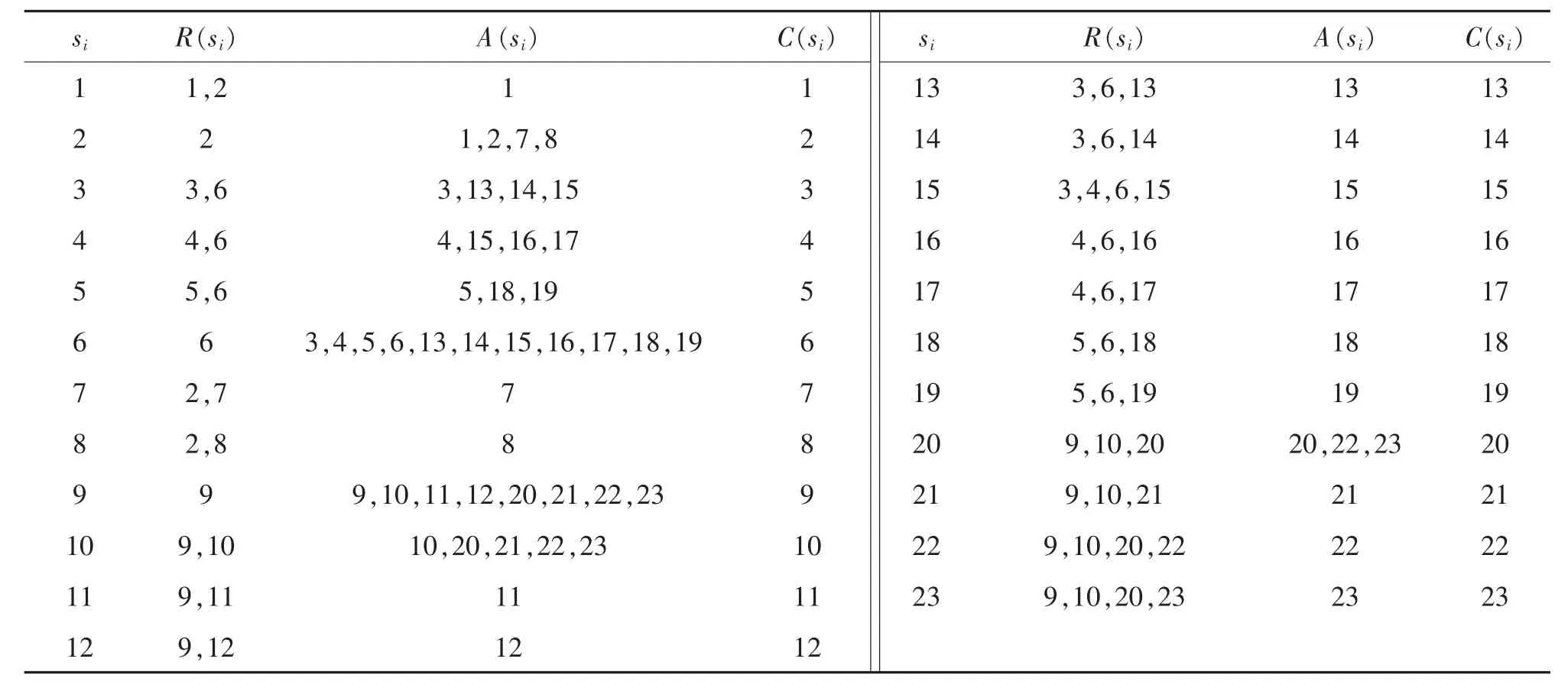
表2 可达集、先行集和共同集表Tab.2 R(si)、A(si)and C(si)
由表 2可知,先行集 B(si)={s1,s7,s8,s11,s12,s13,s14,s15,s16,s17,s18,s19,s21,s22,s23},其中,{s1,s7,s8},{s11,s12},{s13,s14,s15,s16,s17,s18,s19},{s21,s22,s23}分别属于不同的区域。
从上述表中找出满足C(si)=R(si)的要素,为2,6,9,这些元素表示与其可达集中的要素构成回路,没有更上一级的要素,即位于解析结构模型中最顶层的要素。
1.3 级间分解得出结果
通过级间分解得出的各个要素的级别,可以确定出制约轨道交通与常规公交接驳的解析结构模型,如图2。
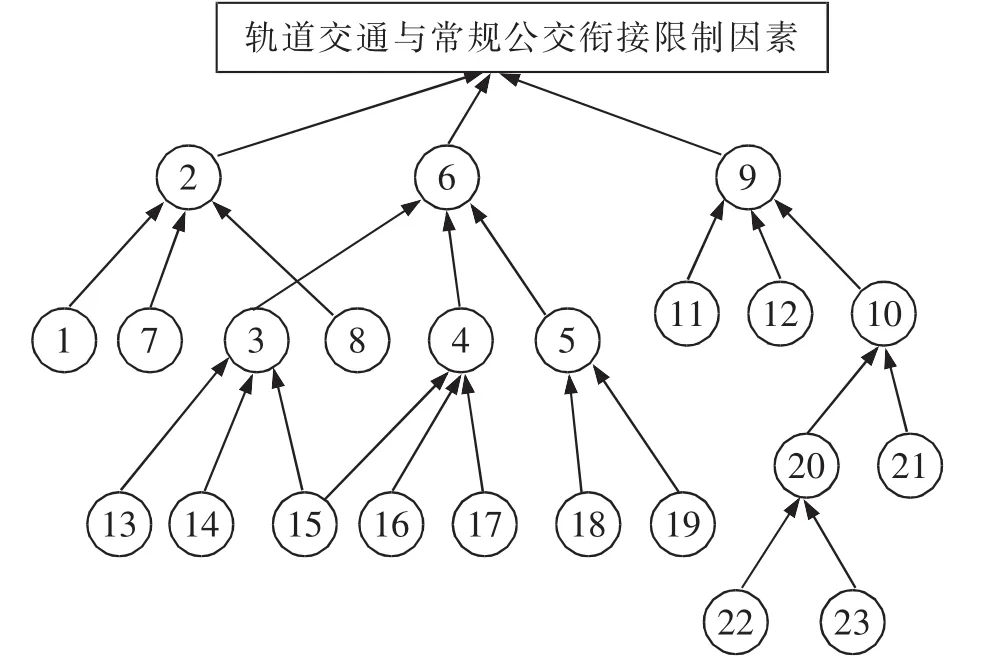
图2 制约因素解析结构模型Fig.2 Interpretive structure modeling of restriction factors
通过分析可以得出,影响城市轨道交通与常规公交接驳最主要的制约因素是:规划不同步、基础设施不合理(包括路网和站点)、运营管理的欠缺。由于轨道交通与常规交通分属不同的主管部门,发展阶段也有所差异,因此没能统筹规划管理,对接运线路和枢纽的建设各自为政。再加上二者技术经济特征各有优势,部分线路重合,造成它们之间存在竞争。在城市轨道交通发展初期,对接驳设施的建设重视程度不够,给旅客换乘带来不便。由于科学技术不够先进,接驳信息的发布不及时,乘客等车时间过长,不少乘客不愿选择换乘。这些都给轨道交通和常规公交的发展造成了阻碍。
2ISM-Fuzzy AHP分析
在上述所求出的解析结构模型基础上,还需采用模糊层次分析法(Fuzzy AHP)对各影响因素进行定量分析,求得表示各因素相对于各层其他因素重要程度的权重值。
模糊层次分析法是将模糊数学理论运用到层次分析法中,在解决多准则和多方案问题方面有着广泛的运用。它对于AHP的优点在于判断矩阵的模糊性,简化了人们判断目标相对重要性的复杂程度,并借助模糊判断矩阵实现决策由定性向定量方便、快捷的转化,直接由模糊判断矩阵构造模糊一致性判断矩阵,使判断的一致性得到解决。运用该方法对轨道交通与常规公交衔接影响因素的解析结构模型进行分析。
2.1 构造三角模糊数互补判断矩阵
判断矩阵的作用是在上一层某元素的约束条件下对同层次元素之间的相对重要性进行比较,考虑到人的模糊性,用三角模糊数M0.5,M0.6,M0.7,M0.8,M0.9以及M0.1,M0.2,M0.3,M0.4(如图3)来定量表示因素间的两两比较判断。

图3 三角模糊函数的特征函数Fig.3 The characteristic function of triangular fuzzy function

2.2 计算初始权重(单层次因素综合模糊值)
根据已建立的n×n阶模糊判断矩阵,进行其单层次重要性权重计算,也称为单层次排序,即同一层次相应元素对于上一层次某因素相对重要性的排序,该过程是某因素相对于更高层次其他因素重要性权重计算的基础,假设第k层指标i的初始权重为,则

2.3 去模糊化计算各指标的最终权重
由于获得的三角模糊权重还不是所需的因素权重信息的完全确知状态,还要把各因素的初始模糊权重进行两两比较建立可能度矩阵P=(pij)n×n,其中的可能度,即对于三角模糊数和
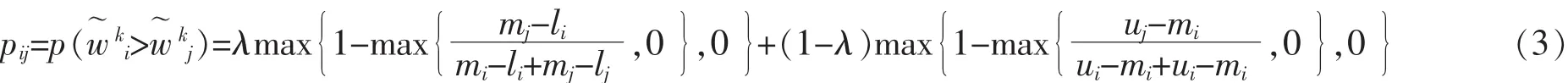
其中λ∈[0,1],当λ>0.5时,称决策者是追求风险的;λ=0.5时,称决策者是风险中立的;当λ<0.5时,称决策者是风险厌恶的(本文取λ=0.5)。
这样对三角模糊数进行排序就转化为求解可能度矩阵的排序向量ω=(ω1,ω2,…,ωn)T,ωi可以按式(4)计算[11]:

2.4 各层次相对指标权重
由于在解析结构模型中,不同的影响因素之间通过层级关系产生相互影响,因此对于某一影响因素,还需计算该因素对其他任意目标层的其他因素的相对权重,即计算组合权向量。
设第k层包含nk个影响因素,其相对于k-1层某一影响因素Aik-1的层次单排序权重分别为ω1ik,ω2ik,…,ωnkik(当Aik与Aik-1无关联时,Aijk=0),同理k-1层影响因素相对于k-2层影响因素Aik-2的层次单排序权重分别为 ω1xk-1,ω2xk-1,…,ωnk-1xk-1,则第k层各影响因素相对于第k-2层影响因素Ajk-2的权重按式(5)计算:

3 西安地铁3号线与公交换乘实例分析
根据西安市城市快速轨道交通建设规划调整(2013—2021年)方案,到2021年,将形成7条运营线路(1~6号线及临潼线)、总长243.2 km的轨道交通网络。目前西安共开通地铁3条,总长91.2 km,西安地铁2号线开通5年,1号线开通3年,西安地铁3号线于2016年11月正式运营,总长39.9 km。城市轨道交通投资大、建设周期长,根据ISM-Fuzzy AHP分析,建立该3个因素之间的模糊判断矩阵如表3所示。
按照以上步骤对该矩阵进行计算处理, 得到第 1层 3个影响因素的最终权重为:(ω12,ω16,ω19,)=(0.359,0.592,0.049),因此对于西安地铁和公交换乘的影响因素6相比于影响因素2和9来说作用更大。按照同样的方法,对其他因素采用专家咨询意见构造模糊判断矩阵进行分析得到的各因素对于其上一级的权重 分 别 为 :(ω21,ω28,ω28,)=(0.384,0.539,0.077),(ω23,ω24,ω25,)=(0.516,0.119,0.365),(ω211,ω212,ω210,)=(0.316,0.516,0.167),(ω313,ω314,ω315,)=(0.612,0.076,0.312),(ω315,ω316,ω317,)=(0.516,0.316,0.167),(ω318,ω319)=(0.71,0.29),(ω320,ω321)=(0.625,0.375),(ω422,ω423)=(0.744,0.256), 由于第一层的权重排序为 ω16,ω12,ω19,,通过公式(5)还可计算出第3层因素相对于因素6的权重如表4所示。
根据表4中的结果,可以找出对于因素6的主要影响因素是公交站点设置等基础设施布局方面,并建议采用以下调整措施:

表3 3个因素之间的模糊判断矩阵Tab.3 Fuzzy judgment matrix among the three factors

表4 第3层因素相对于因素6权重排序Tab.4 The third-layer weights in factor 6
1)对于与3号线重合站点数不超过3个、与3号线属于交叉关系的公交线路,应予以保留。如41,503,508、教育专线等。
2)为了方便乘客换乘,地铁3号线站点位于公交站两站中间的公交,建议将公交站调整延伸至地铁站,如地铁北池头站现在位于41路西影路公交站和观音庙公交站中间。
3)对于以3号线站点为起讫点向两侧辐射的中、长距离公交线路,保留为接运公交线路。如:21,22,106,313,509,410,504,204,K631,224,715等。
4)对于重合部分公交线路站距较短,可以方便3号线站点间短途出行的线路,予以保留。如14,34,400,24,716,环1,环2,604等。
此外,用相同的办法可以对因素2和9进行权重计算,对于因素2,第2层影响因素7对因素2影响最大,占0.539,对于因素9,第2层的因素11影响程度最大,占0.516,而第4层的因素22,所占权重仅为0.078。
根据计算结果提出以下综合改进建议:
1)主管部门协作,统筹规划管理。只有这样才能把轨道交通和常规公交各自的发展置于整个城市交通体系中,充分考虑制约因素,提高工作效率,从宏观上把握二者的顺利接驳。
2)对现有常规公交的线路和站点进行调整。
3)开通接运公交。方便地铁站点2 km范围内的居民出行换乘,并在高峰时刻增加发车频率,满足人们的出行需求,减轻车内拥挤情况。
4)地铁站附近设置自行车停放处。鼓励人们选择自行车,特别是公共自行车出行,方便自行车与轨道交通的换乘。而且能够减轻交通压力,节能环保。
5)加快信息流通,及时发布接驳信息。例如在地铁站内设置大屏幕,提示附近可换乘的公交站点、距离、平均候车时间、途径站点等信息,方便人们选择最优的线路,节省出行时间。
6)改善常规公交的候车环境。设置必要的遮风挡雨设施,尽量避免人流车流混乱。
4 结语
城市轨道交通与常规公交都是城市公共交通的重要组成部分,本文在了解了国内外相关领域的研究现状基础上,运用系统工程中的解析结构模型和模糊层次分析法,对城市轨道交通与常规公交的衔接做了系统而全面的分析。主要的工作和结论有:
1)对国内外城市轨道交通与常规公交的研究现状做了分析与总结,提倡借鉴国外先进的经验,发展我国的城市公共交通。
2)用ISM模型对轨道交通与常规公交接驳中的影响因素进行分析,建立了因素之间的解析层级结构,使各因素间的影响关系明确化。
3)以西安地铁3号线与常规公交换乘为例,定量分析了二者之间影响因素的各级权重,并根据实际的地铁规划布局对现有公交线路进行调整,实现二者有效协调衔接,以便更好地发挥城市公共交通的运输能力,满足人们日益增长的出行需求。
[1]陈扶.国内外城市轨道交通与常规公交一体化启示[J].都市快轨交通,2011,24(3):43-45.
[2]邓连波,高伟,赖天珍,等.基于换乘网络的城市轨道交通关联公交接驳线网优化[J].铁道科学与工程学报,2012,9(6):77-83.
[3]林世生.城市轨道交通与常规公交衔接探析[J].现代城市轨道交通,2007(1):51-53.
[4]谢玉洁,韩宝明,许惠花.城市轨道交通与地面常规公交的客运一体化[J].都市快轨交通,2006,19(1):32-34.
[5]HUO Y,ZUO D,MA L.Comprehensive evaluation of urban rail transit network planning based on super efficiency DEA and triangular fuzzy AHP[C]//Cota Znternational Confernce of Transportation Professionals,2015:3626-3633.
[6]SHI J J,XUE Y X.Logistics performance evaluation based on triangular fuzzy AHP and super efficiency DEA method[J].Logistics Sci-Tech,2013,36(7):62-64.
[7]尹洪英,徐丽群,权小锋.基于解释结构模型的路网脆弱性影响因素分析[J].软科学,2010,24(10):122-126.
[8]孙慧,周颖,范志清.基于解释结构模型的公交客流量影响因素分析[J].北京理工大学学报:社会科学版,2010,12(1):29-32.
[9]吴贞瑶,云雅倩.基于解释结构模型的城轨客流量影响因素分析[J].科技资讯,2014,12(8):245-246.
[10]张晶,郑长江,耿扬.拥堵收费对城市居民外外通勤方式的影响分析[J].华东交通大学学报,2016,33(4):94-97.
[11]和媛媛,周德群,王强.基于可能度的三角模糊数互补判断矩阵排序方法[J].运筹与管理,2009,18(1):65-68.
Rail Transit and Bus Interface Optimization Based on ISM-Fuzzy AHP Model
Liu Xinmeng
(School of Economic Management,Xi’an Aeronautical University,Xi’an 710077,China)
It is urgent to improve public transportation service level with the organic combination of urban rail system and bus transit system as well as public traffic integration,which meets the request of transit priority policy in cities in China.This paper analyzed the role of the development of urban rail transit in public transportation system,built up the multilevel hierarchical structure for the factors affecting the connection between rail transit and conventional bus using interpretative structure model,and determined the weight vector for each level using fuzzy analytic hierarchy process.Combining the qualitative analysis with the quantitative analysis,it researched the optimization of connection between rail transit and conventional bus and verified the method with the practical example of Xi’an Metro Line 3.
urban rail transit;public transportation system;connection;interpretative structure model;fuzzy analytic hierarchy process
U116.2
A
1005-0523(2017)03-0066-07
(责任编辑 刘棉玲)
2016-11-27
西安航空学院校级科研基础基金项目(2017KY2233)
刘欣萌(1991—),女,助教,硕士研究生,研究方向为交通运输现代组织管理理论与方法。
