基于双层规划的公共电动自行车租赁点选址模型*

胡郁葱 陈枝伟† 黄靖翔

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.现代城市交通技术江苏高校协同创新中心， 江苏 南京 210000)

基于双层规划的公共电动自行车租赁点选址模型*

胡郁葱1,2陈枝伟1,2†黄靖翔1,2

(1.华南理工大学 土木与交通学院， 广东 广州 510640； 2.现代城市交通技术江苏高校协同创新中心， 江苏 南京 210000)

建设公共电动自行车系统是有效利用资源、满足居民经济低碳出行需求的可行途径之一.文中提出了公共电动自行车网络系统的概念，并采用出行链对其进行分析.在此基础上，建立双层规划模型解决该网络系统中的租赁点选址问题.上层模型考虑政府的目标，为系统最优模型；下层模型考虑用户的目标，为用户均衡模型.上层模型采用混合粒子群优化算法求解，下层模型采用Frank-Wolfe算法求解.算例结果表明，文中算法能够同时确定站点选址和站点规模，收敛性能较好.

公共电动自行车；选址模型；双层规划；混合粒子群优化

近年来，公共自行车在许多城市取得了较大发展[1].但自行车出行耗费体力，骑行距离有限，骑行体验受环境影响较大，正日益被更为舒适、省力、低碳、骑行距离长的电动自行车所代替.在此背景下，发展公共电动自行车，无疑是有效利用资源、满足居民经济低碳出行需求的可行途径之一.

租赁点选址是建立公共电动自行车系统的重要环节，其合理与否直接决定系统建设的成败.与自行车不同，电动自行车需要充电，因此充电桩的配置对租赁点的选址具有重要影响.此外，电费是系统运营成本的主要部分，这使得未考虑充电问题的公共自行车租赁点选址理论并不直接适用于公共电动自行车租赁点的选址实践，因此，有必要对公共电动自行车租赁点的选址模型进行研究.

目前国内外在公共自行车租赁点选址方面的研究成果较多，主要包括经验选址法[2]、考虑库存的枢纽位置选址模型[3]、中心弧选址模型[4]、排队论模型[5]、双层规划模型[6]、OR模型[7]等.尽管公共自行车租赁点选址模型不断完善和发展，但一些关键问题仍未解决：①一般对“步行、借车、骑行、还车、步行”这一完整的公共自行车使用过程考虑不足；②未能综合考虑出行时间和租赁费用给用户带来的出行成本等.国内外目前尚无对公共电动自行车租赁点选址模型的研究，特别是没有考虑电动自行车的充电问题.

为解决上述问题，文中定义了公共电动自行车网络系统，引入出行链的概念，考虑公共电动自行车系统规划者和用户之间的互动作用，分别从系统最优和用户均衡的角度建立上、下层模型，从而构建起公共电动自行车租赁点选址的双层规划模型.

1 公共电动自行车网络系统

公共电动自行车网络系统由不同的公共电动自行车出行链和出行链上的公共电动自行车租赁点构成.

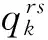
1.1 出行链和广义出行成本

出行链是指用户从起点到讫点的单向出行过程，包括5个阶段：①从交通小区r步行至借车点m；②在借车点m借车；③使用公共电动自行车从借车点m骑行至还车点n；④在还车点n还车；⑤从还车点n步行至交通小区s.用户使用公共电动自行车的成本不仅包括骑行时间，还包含步行时间和在租赁点的逗留时间.此外，租赁费用也是出行成本的一部分.因此，用户在OD对(r,s)间的第k条出行链的广义出行成本为

(1)

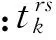
(2)

1.2 公共电动自行车租赁点和逗留时间

公共电动自行车租赁点由充电桩和公共电动自行车构成.充电桩应具有刷卡借还车功能(无刷卡借还车功能可配备独立的智能租赁终端).租赁点的规模由充电桩数量ux和配备的公共电动自行车数量bx确定,

(3)

式中：φpile,x为租赁点x的充电桩周转率；φbike,x为租赁点x的自行车周转率；qx为租赁点x的公共电动自行车流量，

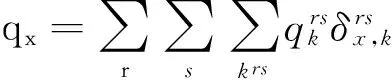
公共电动自行车租赁点的3个因素对租赁点的选址具有决定性的影响：

1)高密度的租赁点布局需要大量的投资且会导致租赁点服务范围的大量重叠,因此，两个租赁点之间距离不宜过近,其最小距离等于两个租赁点服务半径之和.

2)电动自行车一次充电后的续航里程决定了借车点和还车点之间的最大距离.

3)用户在借还公共电动自行车的过程中，可能会由于车辆充电而产生等待时间，因此充电效率是影响逗留时间(等待时间和借/还车时间之和)的一个重要因素.公共电动自行车租赁点可以视作M/M/c排队系统.在假设顾客到达服从泊松流、各充电桩服务时间服从负指数分布且工作相互独立的条件下，租赁点x的逗留时间的计算公式为

(4)

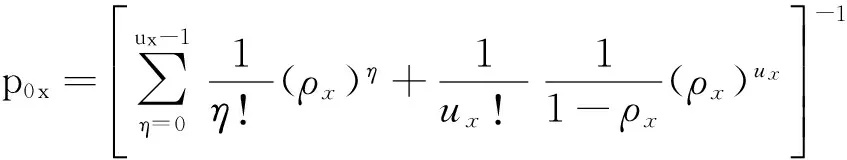
1.3 步行时间和骑行时间

假设交通小区出行需求均匀分布，则OD对(r,s)之间的出行可看成从r的形心到s的形心的过程.因此，步行时间的计算公式如下：

(5)

式中，Srm为从r的形心到借车点m的距离，Sns为从还车点n到s的形心的距离，vw为步行速度.

骑行时间为用户使用公共电动自行车在借车点m和还车点n之间骑行的时间.由于电动自行车车速较低，所以同一出行链的骑行时间主要受行程距离的影响.此外，电动自行车专用道可以使得电动自行车获得独立路权并实现恒速行驶.综上所述，骑行时间计算公式为

(6)

式中：t0mn为从借车点m到还车点n的电动自行车自由流的行驶时间；Cmn为借车点m和还车点n之间路段的实际通行能力；α、β为待标定参数；Smn为借车点m和还车点n之间的距离；ξ为速度折减系数(当设置电动自行车专用道时ξ=1，否则ξ<1)；vc为自由骑行速度；qmn为m和n之间的公共电动自行车流量，

2 公共电动自行车租赁点选址的双层规划模型

2.1 模型的假设条件

根据以上分析，文中所建模型的假设条件如下：①出行链是单向的；同一租赁点在两条反向出行链中功能相反；②各租赁点的电动自行车供应量充足，不考虑公共电动自行车的平衡问题；③出行需求在交通小区内均匀分布，因此将小区形心视作出行需求点;④用户到达服从泊松分布；各充电桩工作相互独立且服务时间服从负指数分布；⑤电网能力能够满足公共电动自行车系统的建设运营要求.

2.2 双层规划模型构建

文中所述租赁点选址问题兼顾政府和系统用户的两层目标，因此选用双层规划模型来建模.

在建设公共电动自行车系统时，政府部门希望系统的效益最大化，即出行者出行成本之和最小.因此，上层模型为系统最优问题，需要满足的约束条件是：①两租赁点之间的距离满足最小、最大距离的限制；②至少选择一个借车点；③至少选择一个还车点；④各租赁点建设运营资金之和不大于投资总额上限；⑤各出行链上的公共电动自行车出行量之和等于小区之间的电动自行车出行需求量；⑥各出行链上的公共电动自行车出行量为非负值.

(7)

s.t.

式中，dmin、dmax分别为两租赁点之间的最小距离和最大距离，I为投资总额上限，ix为租赁点x的建设运营费用.其余参数定义见第2部分.

公共电动自行车用户总是希望花费在出行上的时间尽可能少，所以他们总是寻找最短路出行.因此，下层模型为用户均衡模型.

(8)

s.t.

2.3 模型求解算法

由于粒子群优化算法实现简单，收敛速度快，鲁棒性强[8]，文中选择其改进算法——混合粒子群优化来求解上层模型.相对于传统的用户均衡模型而言，下层模型的求解规模更小(每条出行链仅有4个节点且租赁点数目有限)，所以文中选用传统的Frank-Wolfe算法来求解下层模型.

根据模型的数学特性，发现通过在上层模型和下层模型之间反复迭代可以逐渐逼近双层规划模型的最优解，具体流程如下.

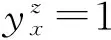
步骤4 判断结果是否满足迭代停止条件

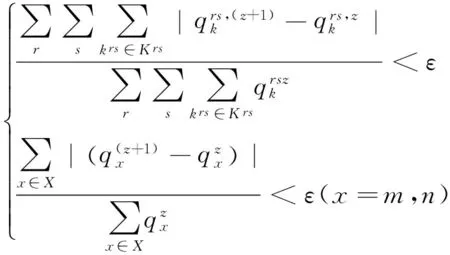
式中，ε为可接受误差.

若满足，则输出全局最优解；若不满足，令z=z+1，返回步骤2继续求解.

3 算例分析

3.1 算例背景

以华南理工大学五山校区的两个交通小区(M和N)为例说明文中研究的模型在公共电动自行车租赁点选址决策中的应用.根据与地铁站距离、重要集散点位置等因素初步筛选得到9个备选公共电动自行车租赁点，如图1所示.两个交通小区之间的高峰小时公共电动自行车潜在需求量为1 000次/时.距离信息如表1、2所示，成本信息和其他相关参数如表3所示.

图1 备选公共电动自行车租赁点

Table 1 Distance from centroids of traffic zones to candidate sites km

表2 租赁点到租赁点的距离

Table 2 Distance from pick-up stations to drop-off stations km

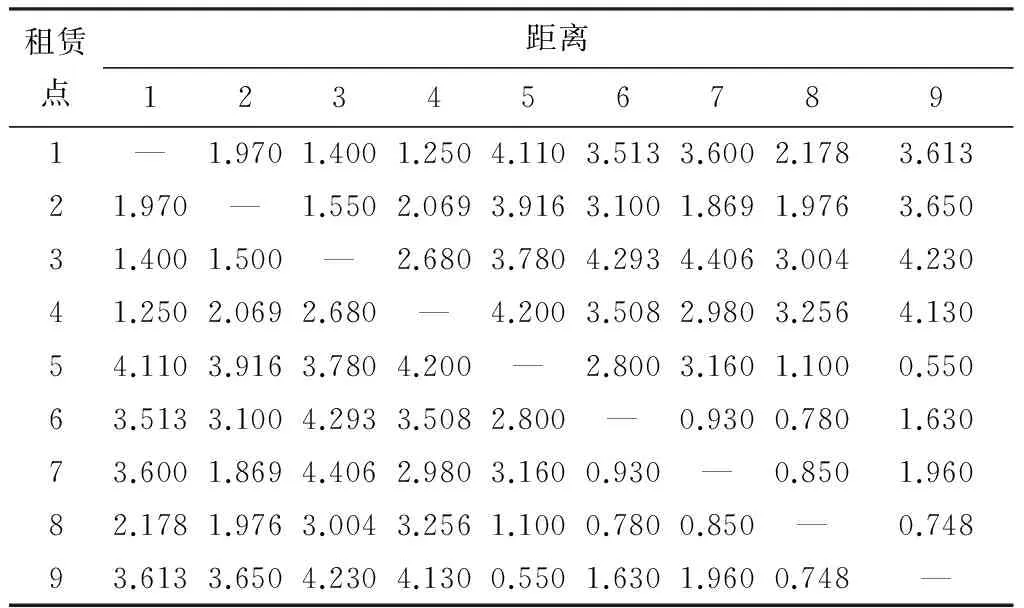
表3 租赁点成本信息及相关参数

Table 3 Cost information of electric bicycle stations and other relevant parameters

参数取值说明参数取值说明电动自行车价格cb/(元·车-1)1800根据市场调查得到的平均价格充电桩价格cp/(元·桩-1)4000根据市场调查得到的平均价格c/(元·h-1)1.5电动自行车的电费/(元·h-1)50根据2015年广州市人均工资估算日建设费用ci/(元·天-1)500根据广州公共自行车系统的成本数据估算(考虑电费)年运营费用(含电费)co/(元·站-1·年-1)4200根据广州公共自行车系统的成本数据估算(考虑电费)α0.05根据参考文献数据调整[10]β1根据参考文献数据调整[10]租赁点的年平均费用i=cbbm+cpum+365ci+coξ0.9根据参考文献数据调整[10]vw/(km·h-1)3.96人类平均步行速度Cmn1500实地调查获取vc/(km·h-1)15平均电动车骑行速度dmin/km1服务半径[11]φpile/(桩·h-1)30根据广州公共自行车系统的数据估算φ车/(车·h-1)36根据广州公共自行车系统的数据估算dmax/km25电动自行车充满电后的续航里程[12]I/百万元0.3华南理工大学基建处工作人员估算

3.2 结果分析

在一台装有Windows 7.0(专业版)系统的笔记本电脑上采用Matlab语言实现本算法.其中，上层模型的罚函数构造规则为：若不符合约束条件①、②或③，罚10 000；若不符合约束条件④，罚30 000；下层模型保证约束条件⑤和⑥会得到满足，故无需对其构造罚函数.混合粒子群优化算法的粒子数取20，最大迭代次数取100.可接受误差取0.03.算法运行结果如表4所示，算法收敛性能分别如图2、3所示.

从表4看到，交通小区M应该建设租赁点 1(13个充电桩和18辆公共电动自行车)；交通小区N应该建设租赁点8(26个充电桩和37辆公共电动自行车).租赁点1位于地铁站附近，使用公共电动自行车接驳需求较大.租赁点8靠近区N的形心，集中了学生宿舍、学生食堂、运动场等生活设施，是该小区的交通需求聚集地.因此，采用文中所述模型的租赁点选址结果与实际情况较为接近，具有一定的现实意义.

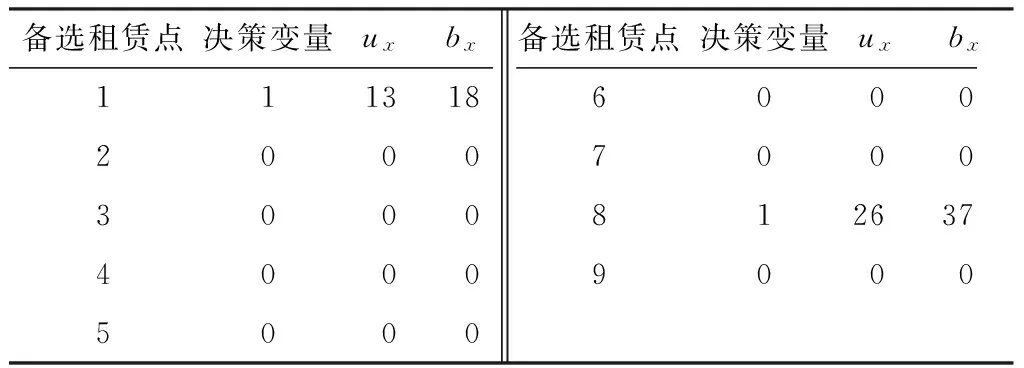
表4 算法运行结果

图2 迭代次数和相对误差的关系

图3 迭代次数和运行时间的关系

从图2可以看到，在可接受误差为0.03的条件下，算法迭代153后收敛.qmn、qm和qn的相对误差是0.029 74、0.010 18和0.020 16.从图3可以看到，算法总运行时间42 s. 因此，混合粒子群算法收敛性能好，收敛速度快.

4 结语

文中在分析了公共自行车租赁点选址方法的研究现状后，针对其中的不足提出了基于双层规划的公共电动自行车租赁站点选址方法，采用双层规划模型描述该选址问题：上层模型从政府的角度出发，在各种约束前提下，设计合理的租赁点布局，使得公共电动自行车出行达到系统最优；下层模型则从用户的角度出发，采用用户均衡模型来描述公共电动自行车用户的出行行为.上层模型采用混合粒子群优化算法求解，下层模型采用Frank-Wolfe算法求解.算例的结果表明，该算法能够同时确定站点选址和站点规模(包括充电桩数目和配备电动自行车的数目)，算法收敛性能较好，能够为政府部门的决策提供科学的依据.

[1] ELLIOT Fishman.Bikeshare：a review of recent literature [J].Transport Reviews,2015,36(1):92-113.

[2] 朱玮,何京洋,王德.法国公共自行车系统布局方法与实证研究——以巴黎和里昂为例 [J].国际城市规划,2015,30(Z1):64-70. ZHU Wei,HE Jing-yang,WANG De.Methods and empirical research on the distribution of public bicycle systems in France:case study on Paris and Lyon [J].Urban Planning International,2015,30(Z1):64-70.

[3] LIN Jenn-rong,YANG Ta-hui.Strategic design of public bicycle sharing systems with service level constraints [J].Transportation Research Part E,2011,47(2):284-294.

[4] CAMPBEL James,ERNST Andreas,KRISHNAMOORTHY Mohan.Hub arc location problems:Part II-formulations and optimal algorithms [J].Management,2005,51(10):1556-1571.

[5] GEORGE David,XIA Cathy.Fleet-sizing and service availability for a vehicle rental system via closed queueing networks [J].European Journal of Operational Research,2011,51(10):198-207.

[6] 李婷婷.城市公共自行车租赁点选址规划研究 [D].北京:北京交通大学,2010.

[7] 潘雪.基于多目标优化的城市公共自行车租赁点选址研究 [D].沈阳:沈阳工业大学,2016.

[8] ZHANG Yun-dong,WANG Shui-hua,JI Gen-lin.A comprehensive survey on particle swarm optimization algorithm and its application [J].Mathematical Problems in Engineering,2015,2015(1):1-38.

[9] 薛峰,陈刚,高尚.求解0-1整数规划的混合粒子群优化算法 [J].计算技术与自动化,2011,30(1):86-89. XUE Feng,CHEN Gang,GAO Shang.Solving 0-1 integer programming problem by hybrid particle swarm optimization algorithm [J].Computing Technology and Automation,2011,30(1):86-89.

[10] 张巧.混合交通流条件下城市路段BPR函数参数标定研究 [D].长沙:中南大学,2013.

[11] GUO Tang-yi,ZHANG Ping,SHAO Fei,et al.Allocation optimization of bicycle-sharing stations at scenic spots [J].Journal of Central South University,2014,21(8):3396-3403.

[12] 电动自行车通用条件:GB17761—1999 [S].

Location Model for Public Electric Bicycle Rent Based on Bi-Level Programming

HUYu-cong1,2CHENZhi-wei1,2HUANGJing-xiang1,2

(1.School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China;2.Jiangsu Province Collaborative Innovative Center of Modern Urban Traffic Technologies, Nanjing 210000, Jiangsu, China)

Developing public electric bicycle systems is a feasible way to making full use of resources and meeting people’s increasing demand for low-carbon trips. This paper first proposes a public electric bicycle network system based on trip chain analysis, and then establishes a bi-level programming model to solve the station location problem of such systems. In this model, the upper part considers the government’s goal for system optimization, while the lower part shows respect for system users’interests and user equilibrium. The upper model is solved by using the hybrid particle swarm optimization algorithm and the lower one is solved by using Frank-Wolfe algorithm.Numerical results show that the proposed programming model can determine both the optimal location and the size of stations in the public electric bicycle network system with good convergence.

public electric bicycle; station location model; bi-level programming; hybrid particle swarm optimization

2016-06-01

国家自然科学基金资助项目(51408237);国家级大学生创新创业训练计划项目(201510561102) Foundation items: Supported by the National Natural Science Foundation of China(51408237) and the National College Students Innovation and Business Plan(201510561102)

胡郁葱(1970-)，女，博士，副教授，主要从事交通运输规划与管理研究.E-mail:ychu@scut.edu.cn

† 通信作者: 陈枝伟(1994-),男，主要从事交通运输规划与管理研究.E-mail：c.zw02@scut.edu.cn

1000-565X(2017)04-0118-06

U 491.2

10.3969/j.issn.1000-565X.2017.04.017