一种基于轴承剩余寿命预测的状态维修优化决策方法
2017-06-19徐廷学
徐廷学,张 众
(海军航空工程学院,山东 烟台 264000)
一种基于轴承剩余寿命预测的状态维修优化决策方法
徐廷学,张 众
(海军航空工程学院,山东 烟台 264000)
针对以往研究中状态维修的关键环节,剩余寿命预测不能更新的问题,提出一种融合贝叶斯方法的神经网络退化预测模型,实现利用实时传感信号动态预测轴承的剩余寿命分布。检验结果表明,该模型对轴承的剩余寿命预测比较精确。基于更新的剩余寿命分布,建立了以费用率最小为目标的轴承状态维修优化决策模型,求解得到最优的轴承预防性更换时间。
工业工程学;神经网络; 贝叶斯方法; 振动频谱;剩余寿命分布; 维修决策
随着武器装备集成度不断提高,复杂性不断增加,装备维护成本也相应提高[1]。其中由于突发故障带来的维修费用和停机损失在装备维护成本中占到相当大的比例。传统的事后维修和定时维修都不能很好地应对突发故障带来的非计划维修,易造成“过维修”和“欠维修”等问题[2]。基于状态的维修(CBM)决策技术是在检测、评估设备状态的基础上,选择合理的维护方式,以最小期望费用率、最高可用度为目标,进行最优维护策略的制定[3]。CBM决策在制定维修策略时综合考虑了系统运行状态和个体差异,能实施更加 “精确”的维修,有效提高维修资源利用率,提高装备完好率和可用度[4]。
实施CBM的关键是对装备状态进行准确评估。而剩余寿命(residualusefullife,RUL)是反映装备状态的综合指标,可作为维修决策的重要依据。目前关于剩余寿命预测已有很多研究方法,然而大部分方法预测的剩余寿命是固定不变的,不能基于在线监测信息进行动态的调整。针对这一问题,笔者提出了一种新的预测方法,将神经网络模型与贝叶斯方法结合,得到可更新的剩余寿命分布,在此基础上建立并求解了以期望费用率最低为目标的轴承状态维修优化决策模型。
1 滚珠轴承的退化
笔者以一组相同的推力滚珠轴承作为样本,研究其退化过程。对轴承的振动信号进行监测,作为退化传感信息的来源。由于监测轴承的成本较低,因而能进行大量的试验,从而确保了验证试验结果的可信性。
1.1 轴承的退化过程
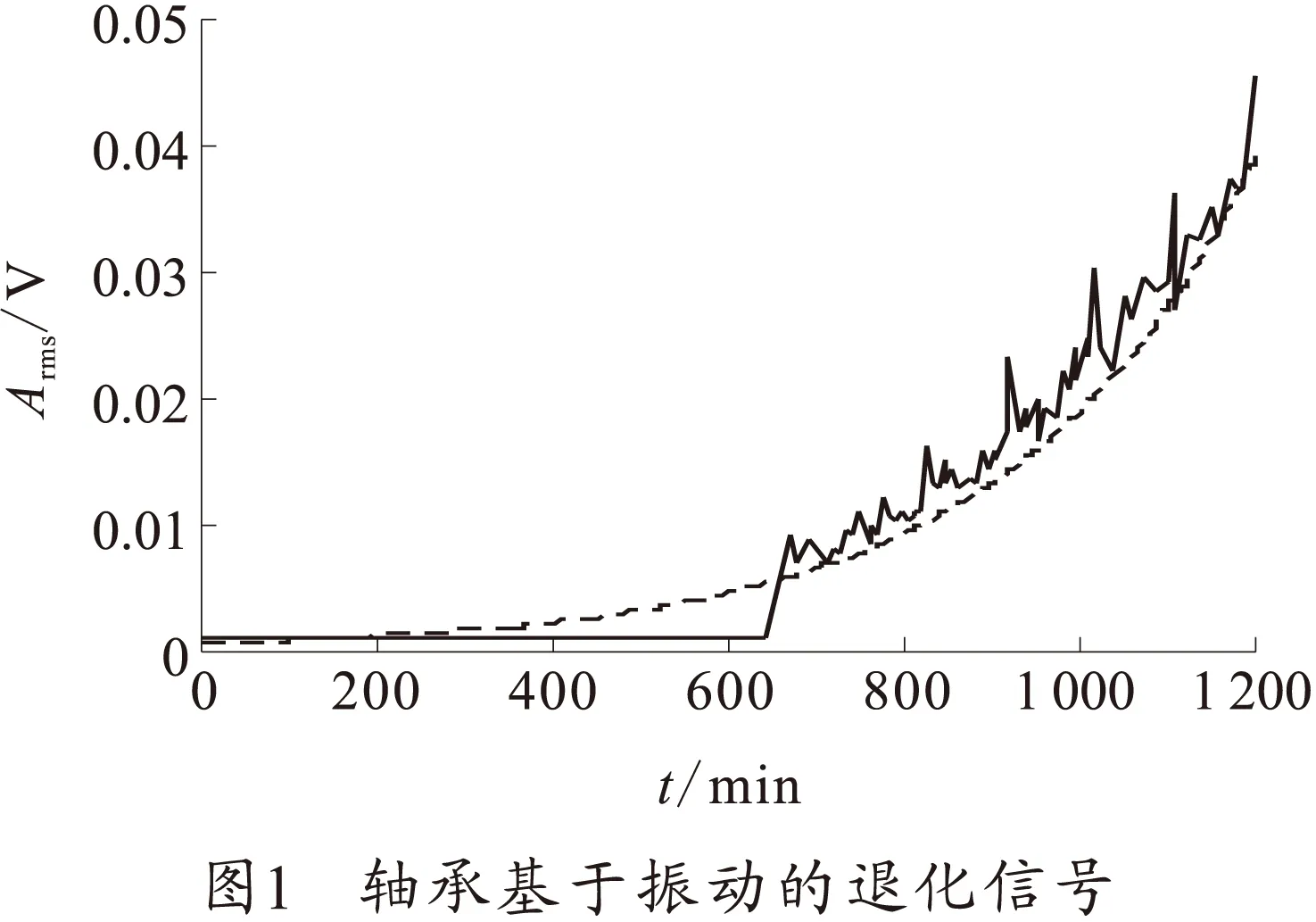
不断运行的轴承会在滚道上产生碎片。滚动体反复通过这些碎片将激发特殊的失效振动频率,同时频率对应的幅值也会随着轴承的失效过程的推移而不断增大[5]。因此可将这种幅频上的增长提取出来,作为轴承的退化信号。
该退化信号由失效频率及其前6个谐波分量对应的平均幅值组成,平均幅值随轴承运行时间变化的趋势如图1所示。碎片的产生带来退化信号中平均幅值的突增,该时间点称为失效时刻。 当振动幅值上升至一个事先确定的故障阈值(设量为Arms=0.03V)时,可判明轴承故障。
1.2 加速退化试验
由于轴承的退化是个较为缓慢的过程。为获得轴承退化、失效和故障数据,考虑对轴承进行加速退化试验。试验中轴承将承受超出额定负载的应力,加速其退化过程,达到缩短测试时间的目的。
本试验中的测试对象为一组向心球轴承,每个轴承包含10个滚珠,将其放入图2所示的加速退化试验装置中,通过液压缸对轴承施加过载的轴向压力,实现轴承退化过程的加速。
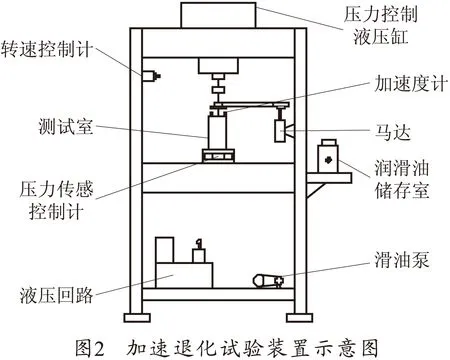
试验是在恒定的运行环境中进行的,其中液压缸对被测轴承传递的轴向压力为1 780N,转速为1 100r/min。文献[6]提供了计算滚珠轴承中钢珠和滚道间压强的公式,计算得到在本试验条件下,钢珠和滚道间的压强为σc=18.63kPa。而生产方规定的钢珠与滚道间的最大压强为σcmax=16.5kPa。因此试验中轴承钢珠承受了超过核定负载的应力,从而加速了其退化过程。
在每次加速试验中,利用加速度计和数据获取系统,可持续采集测试室内轴承的振动频谱,采样间隔为2min。
试验轴承的失效频率可由文献[5]中的方法计算得出,为
fBPF=92Hz
(1)
由机械振动的工业标准ISO2372,定义平均振幅Arms=0.03V为试验轴承的故障阈值。
2 滚珠轴承的剩余寿命分布
2.1BP神经网络建模与权重计算
神经网络可用来寻找网络的输入和输出之间复杂的非线性关系,这是通过网络训练程序实现的[7]。笔者采用BP(BackPropagation)神经网络模型,建立轴承故障时刻和振动频谱之间的关系。该模型包含一组训练过程受监督的前馈反向传播网络。基于一组轴承中第i个轴承Bi的振动信号,可训练对应的神经网络Fi,对轴承Bi的退化过程进行建模。网络数M等于被用来建立退化数据库的测试轴承数量(M=25)。在试验中观察到第1个碎片出现后开始训练网络,并预测轴承故障时刻。
取轴承组中第k个轴承Bk作为验证轴承,Bk在给定采样点n处的幅值向量[Akn]作为网络的输入量,[Akn]被分别输入到25个网络中,得到各网络对Bk的故障时刻预测,与Bk实际故障时刻相比较得到平方误差。
再由式(2),对平方误差做规范化处理,得到网络i的权重:
(2)

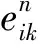
2.2 故障时刻先验分布计算
基于试验观测,选用指数分布形式描述滚动轴承的退化过程。利用式(2)得到的网络权重进行故障时刻预测。计算步骤如下:
1)每个试验轴承的退化信号符合指数分布形式αeβt。这使得有两组指数分布参数组成的向量组{α1,α2,…,α25}和{β1,β2,…,β25}表示受训轴承的退化特征,{α1,α2,…,α25}和{β1,β2,…,β25}的取值可根据各轴承退化信号进行参数估计得到。
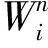
(3)
(4)
3)利用式(5),指数参数可用来计算第k个轴承Bk的故障时刻:
(5)
式中,D为故障阈值。
4)对各采样点,重复步骤2和3,得到一个初始的故障时刻预测样本。利用该样本可计算被监测轴承故障时刻的先验分布。
2.3 故障时刻的后验分布与剩余寿命分布的更新
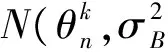
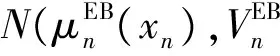
(6)
为了去除剩余寿命为负的值,要将剩余寿命分布以0值截取。则剩余寿命TR的分布函数为
(7)
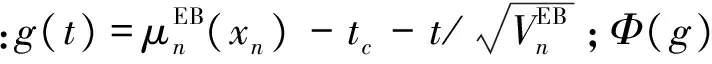
3 基于剩余寿命分布的维修决策优化
在对轴承进行状态监测的基础上,制定如下维修决策流程:

2)当获得一个后续的振动频谱后,将其输入到神经网络模型中,输出一个故障时刻预测值,由贝叶斯公式求得故障时刻的后验分布,再由式(6)更新剩余寿命的分布。在每个采样点,基于新获得的振动频谱,剩余寿命的分布不断得到更新。
3)采取两种维修活动:预防性更换和故障替换。基于更新后的剩余寿命分布,结合维修决策目标,计划在L时刻进行预防性更换。若在预防性更换前发生功能故障(振幅达到故障阈值),则立即进行故障替换。假设采取两种维修活动后系统恢复如新。
在对轴承实施基于状态的维修决策时,需要确定维修决策目标,如安全性、经济性、任务性目标等,然后进行优化求解,获得最优预防维修间隔,从而优化维修活动。
研究在经济性目标约束下的维修决策时,通常以更换周期内单位时间平均费用C(L)为目标函数。设tp和tf分别为预防性更换和故障替换耗费的平均时间;Cp为单次预防性更换费用,包括轴承更换费用和轴承所在系统的停机损失;Cf为单次故障费用,包括轴承更换费用和轴承所在系统的停机损失。
在tc时刻采样获得新的频谱后,剩余寿命分布得到了更新,计划的预防性更换时刻也要重新调整。以轴承开始运行为起点,至L时刻进行预防性更换为终点,构成轴承的一个维修周期。则轴承在一个维修周期内的期望费用CE为
CE=C1+C2
(8)

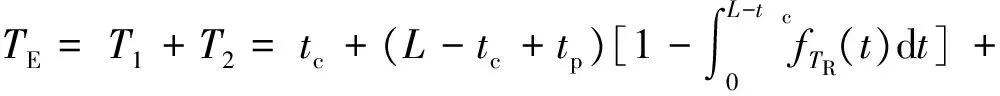
(9)
则在该维修周期内单位时间的期望维修费用为
(10)
于是以单位时间期望维修费用最小为目标,建立轴承的状态维修优化决策模型如下:
(11)
求解该模型,得到最优解L*, 即为轴承的最优预防性更换时刻。
4 模型应用
笔者提出的基于网络神经的退化模型利用另外25个轴承(轴承26~50)来论证。对这些用来验证的轴承(26~50)的退化域进行建模,文中提到退化域开始于第1个碎片的产生,终止于轴承的故障。在每次测试中,持续获得振动频谱并将其用于计算和更新验证轴承的剩余寿命分布。

由式(12)可计算轴承在各采样点的实际故障时刻和期望故障时刻间的误差比:
(12)

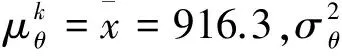
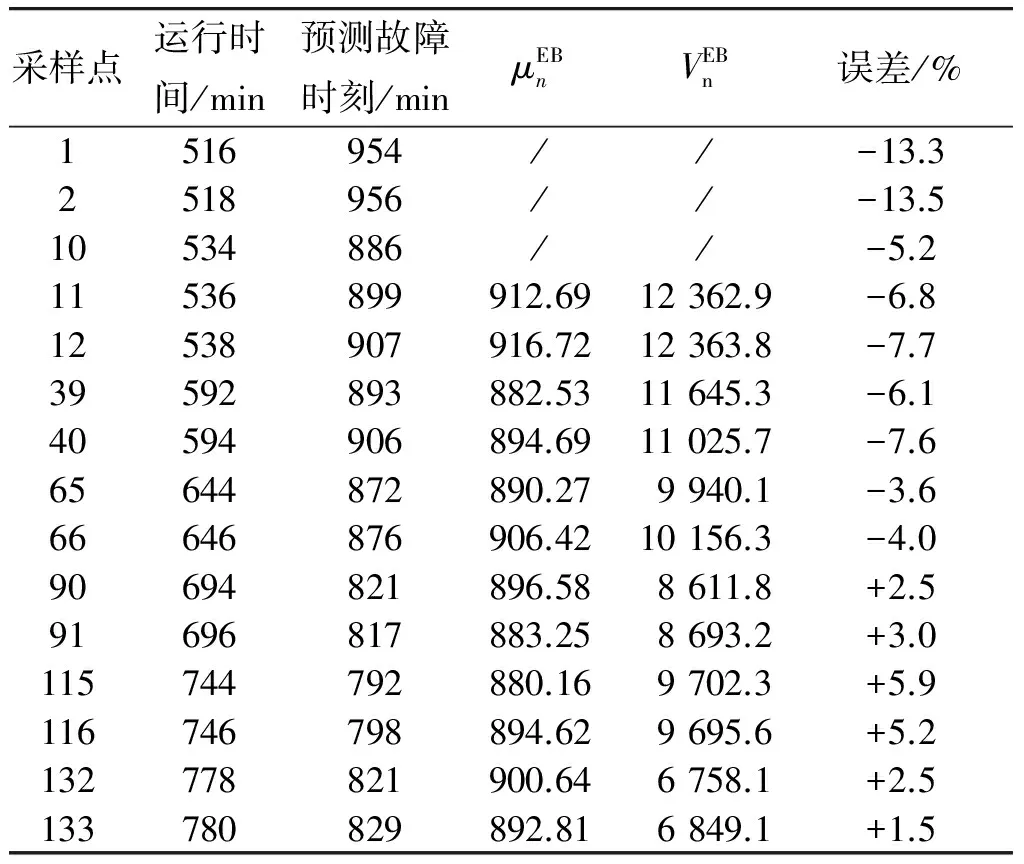
表1 各采样点的参数更新及预测误差情况表
分别计算25个验证轴承的预测误差,得到该模型下故障时刻预测的平均误差绝对值仅为7.56%,预测结果较为精确,证明了该方法的有效性。
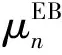
在36号轴承剩余寿命分布更新的基础上,进行状态维修优化决策。以第115个采样点为例,该采样点对应的采样时刻为 744 min。在获得该时刻的振动频谱后,将其输入神经网络,得到一个新的故障时刻预测值,于是得到更新后的剩余寿命分布为

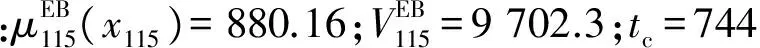
假设轴承预防性更换费用为Cp=80元,预防性更换平均时间tp=6 min,故障替换费用Cf=200元,故障替换平均时间tf=30 min。由式(11),一个更换周期内单位时间费用C(L)为
(13)
通过仿真,平均费用C(L)与预防性更换时刻L的关系如图4所示。

求解式(13)得到在轴承已运行744 min时,最优预防性更换时刻为L=821,即再过77 min,在轴承运行821 min时进行预防性更换,此时更新周期内单位时间平均费用最低,为0.097元/min。
5 结束语
笔者提出了一种基于剩余寿命分布预测的维修决策方法。模型通过滚珠轴承来测试和验证。利用轴承退化时的初始振动信号估计故障时刻的先验分布,再利用后续获得的现场监测值计算后验分布,从而更新剩余寿命分布。由于融入了反应部件实时退化过程的现场监测值,因此可提高故障时刻的预测精度。计算得到模型的平均误差为7.56%,说明预测确实较为精确。在更新后的剩余寿命分布的基础上,以单位时间平均费用最低为目标,求解了最优的预防性更换时刻。
笔者提出的融合实时状态信息与加速试验数据的剩余寿命预测方法,能有效提高预测精度。同时建立了剩余寿命与维修决策目标间的联系,实现了基于剩余寿命预测的状态维修优化决策。笔者设计的加速试验,轴承是在恒定的负载和速度下测试的。下一步可研究改变运行环境带来的影响,并把表示运行环境的参数输入到神经网络中,以实现更符合实际的预测。
References)
[1]周东华,陈茂银,徐正国.可靠性预测与最优维护技术[M].合肥:中国科学技术大学出版社,2013:160- 161. ZHOU Donghua, CHEN Maoyin, XU Zhengguo. Reliabi-lity prediction and optimal maintenance technology[M].Hefei: Press of University of Science and Technology of China,2013:160-161.(in Chinese)
[2]张仕新,昝翔,李浩,等. 状态维修理论及剩余寿命预测的研究现状与展望[J].兵工自动化,2014,33(9):15- 19. ZHANG Shixin, ZAN Xiang,LI Hao,et al. Condition based maintenance theory and the study status and forecast on remaining life prediction[J].Ordnance Industry Automation,2014,33(9):15-19. (in Chinese)
[3]胡剑波,葛小凯,张亮,等.多失效系统退化变迁建模与状态维修决策优化[J].计算机集成制造系统,2014,20(1):165-171. HU Jianbo, GE Xiaokai, ZHANG Liang,et al. Degradation transfer model method and condition maintenance optimizing decision for multiple failure system[J].Computer Integrated Manufacturing,2014,20(1):165-171. (in Chinese)
[4]贾希胜.以可靠性为中心的维修决策模型[M].北京:国防工业出版社,2007:71-98. JIA Xisheng. Maintenance decision model for reliability centered maintenance[M].Beijing: National Defense Industry Press, 2007:71-98. (in Chinese)
[5]HARRIS T A. Rolling bearing analysis[M]. New York: Wiley, 2001:132-134.
[6]BARKER C T, NEWBY M J. Optimal non-periodic inspection for a multivariate degradation mode[J]. Reliabi-lity Engineering and System Safety, 2009,94(1):33- 43.
[7]李国勇.神经·模糊·预测控制及其MATLAB实现[M].北京:电子工业出版社,2013:5-6. LI Guoyong. Nerve, dim, prediction control and its realization by MATLAB[M]. Beijing:Publishing House of Electronics Industry, 2013:5-6.(in Chinese)
[8]仇丽莎,韦来生.正态总体均值和误差方差同时的经验Bayes估计[J].中国科学院大学学报,2013,30(4):454- 461. QIU Lisha, WEI Laisheng. Empirical Bayes estimate of both normal population means and error variance[J]. Journal of University of Science and Technology of China, 2013,30(4):454-461.(in Chinese)
Method of Condition Based Maintenance Optimizing DecisionBased on Residual Life Prediction
XU Tingxue,ZHANG Zhong
(Naval Aeronautical & Astronautic University, Yantai 264000,Shandong,China)
Aiming at the problem of previous studies that the key link of condition based maintenance-residual life prediction always keeps changeless, put forward is a neural net work degradation prediction model which combined Bayes method to predict the residual life distribution of bearing dynamically. The verification results indicate the veracity of the model. Based on the updated posterior residual life distribution, established is the model of minimum expense ratio to maintain and optimize a bearing with the solution to the optimal replacement time of the bearing.
industrial engineering; neural network; Bayes method; vibration spectrum; residual life distribution; maintenance optimizing decision
2015-07-13
国防预研基金资助项目(401080102)
徐廷学(1962—),男,教授,博士,主要从事装备综合保障理论与技术研究。E-mail:xtx-yt@163.com
10.19323/j.issn.1673- 6524.2017.02.017
TJ07
A
1673-6524(2017)02-0078-06
