基于蒙特卡洛法的单全站仪调炮精度测量系统不确定度研究

刘志鹏，李 锴，徐 强

(1.南京理工大学 机械工程学院,江苏 南京 210094；2.湖北江山重工有限责任公司,湖北 襄阳 441057)

基于蒙特卡洛法的单全站仪调炮精度测量系统不确定度研究

刘志鹏1，李 锴2，徐 强1

(1.南京理工大学 机械工程学院,江苏 南京 210094；2.湖北江山重工有限责任公司,湖北 襄阳 441057)

为改进调炮精度测量系统，对单全站仪调炮精度测量系统进行数学建模，采用蒙特卡洛法进行测量精度分析，并在数学模型中修正了测量过程中影响测量精度的主要因素。其测量不确定度与双经纬仪调炮精度测量系统进行了基于蒙特卡洛法的MATLAB仿真计算比较。其仿真结果表明，单全站仪测量系统满足布站距离要求时，测量精度优于双经纬仪调炮精度测量系统，且单全站仪系统操作工作量仅为双经纬仪系统的一半，极大地简化了操作，提高了效率，在调炮精度测量中具有良好的应用价值。

工程测量技术；调炮精度；蒙特卡洛法；不确定度；全站仪；经纬仪

调炮精度是炮兵武器系统重要的战术技术指标之一，是火炮射击时能否能命中目标的关键，直接影响武器系统射击精度。现主要运用的调炮精度测量系统为双经纬仪测量系统，其数学模型是基于空间前方交会测量原理[1]，对两台经纬仪调平要求高，需要进行精确的互瞄操作。近年来新发展出的单全站仪调炮精度测量系统，仅需对一台全站仪进行调平，操作简单方便，提高了测量精度和效率。因两种调炮精度测量系统的数学模型复杂，且具有非线性，导致传统的不确定度计算方法不适用[2-3]。现用蒙特卡洛法对单全站仪调炮精度测量系统不确定度展开研究。

1 单全站仪测量系统和数学模型

1.1 单全站仪测量系统

单全站仪调炮精度测量系统由1台全站仪、便携式PC机、测量软件和数据线等组成，系统如图1所示。单全站仪调炮精度测量系统利用全站仪测距和测角两项功能对身管轴线两标记点进行距离和角度的测量，然后通过测得的4个距离和8个角度求得身管轴线的方向角和高低角的变化，与射击诸元对比可得被测火炮的调炮精度。

1.2 单全站仪测量系统数学模型

根据全站仪测量原理，建立调炮精度测量模型如图2所示。O1为全站仪水平角归零的参考点，O为全站仪中心，P1和P2为炮管两标记点，α1=∠O1OA，β1=∠P1OA，α2=∠O1OB，β2=∠P2OB，l1=OP1，l2=OP2。

火炮初始位置归于零位，调整火炮状态，零位时标记点P1的测量数据为α1，β1，l1，标记点P2的测量数据为α2，β2，l2，据据三角关系可得P1点坐标(x1，y1，z1)和P2点坐标(x2，y2，z2)：

(1)

(2)

(3)

(4)

根据射击诸元(θ，φ)调炮，调炮到位后测量标记点P1′得到测量数据α3，β3，l3,测量标记点P2′得到测量数据α4，β4，l4,跟据三角关系得P1′点坐标(x3，y3，z3)和P2′点坐标(x4，y4，z4)：

(5)

(6)

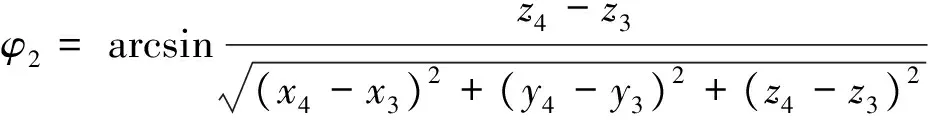
(7)

(8)

推导出高低角调炮精度Δφ和方向角调炮精度Δθ的数学模型为

Δφ=φ2-φ1-φ

(9)

Δθ=θ2-θ1-θ

(10)

2 蒙特卡洛法分析系统不确定度

2.1 蒙特卡洛法

当n个输入量Xi独立时，根据一系列测量值进行分析，确认各输入量Xi的概率分布函数和相关参数。基于MATLAB产生服从相应概率分布的大量随机数，假设从n个输入量Xi的概率分布函数中抽取m个样本值，对于n个输入量，将产生m行n列输入量矩阵xij，i=1,2,…,m；j=1,2,…,n，记为

根据建立的数学模型，计算输入量矩阵式对应每列的函数值，得到m行1列输出量模型值，即为yi。

yi=[y1,y2,…,yi,…,ym]T

(11)

式中，yi=f(xi1,xi2,…,xij,…,xin) 。

利用MATLAB提供的随机数模拟与仿真功能，在确认各个测量输入量的概率分布及数字特征的基础上，得到各个输入量随机抽样的模拟值，进而由计算机计算出相应的输出量的模型值，进一步分析输出量模型值的概率分布，得到与输出量有关的数字特征，这就是蒙特卡洛法实施测量不确定度评定的基本原理和方法[4]。

据统计，截至2017年底，全国创投机构累计投资项目数达到20 674项，累计投资金额4 110.2亿元。其中，2017年当年披露投资项目2 687项，投资金额845.3亿元，平均投资额为3 145万元/项，较2016年大幅增加。

2.2 测量系统不确定度分析

根据双经纬仪数学模型和第1节建立的单全站仪数学模型，确定单全站仪高低角和方向角调炮精度函数v1、w1和双经纬仪高低角和方向角调炮精度函数v2、w2为

v1=Δθ=f(α1,β1,l1,α2,β2,l2,α3,β3,l3,α4,β4,l4)

(12)

w1=Δφ=g(α1,β1,l1,α2,β2,l2,α3,β3,l3,α4,β4,l4)

(13)

v2=Δθ=f(α1,α2,α3,α4,α5,α6,α7,α8)

(14)

w2=Δφ=g(α1,α2,α3,α4,α5,α6,α7,α8,β1,β3)

(15)

其中，变量用Xi表示，其概率分布服从N(μ，σ2)，μ为测量范围内合理的假定值，σ为全站仪和经纬仪的技术指标，测角标准偏差选取2″，测距标准偏差1 mm[5]。

对单全站仪调炮精度测量系统进行误差分析，主要误差来源：全站仪本身测角误差2″，测距误差1 mm；全站仪调平引起的最大垂直角误差3″，水平角误差忽略不计；观瞄手操作引起的测角误差为随机误差，水平角误差1″，垂直角误差2″。根据误差合成原理，确定经纬仪水平角测量误差δ3和垂直角测量误差δ4及测距误差δ5为

δ5=1 mm

2.3 仿真结果

根据实际测量情况选取合适的测量范围，采用基于MATLAB的蒙特卡洛法对测量系统不确定度进行如表1的仿真计算。在测量范围内取200组样本进行仿真得到精度指标，试验中的蒙特卡洛试验次数为M=106，这为调炮角度测量提供95%的包含区间。

表1 两种测量系统不确定度仿真计算表

采用蒙特卡洛法对两种调炮精度测量系统不确定度进行仿真计算，根据MATLAB的输出结果利用Origin得出两种测量系统高低角和方向角的测量标准偏差图表。两种测量系统高低角标准偏差如图3所示，方向角标准偏差如图4所示。

图3、4表明单全站仪调炮精度测量系统在满足布站距离要求时，其测量精度优于双经纬仪调炮精度测量系统。

表2是根据MATLAB的输出结果得到两种测量系统高低角最大标准偏差和平均标准偏差、方向角最大标准偏差和平均标准偏差的统计。仿真结果表明单全站仪调炮精度测量系统精度受全站仪布站距离影响较大，随着布站距离增大，其精度提高。单全站仪调炮精度测量系统在合适的布站距离上其精度全面超越双经纬仪调炮精度测量系统。

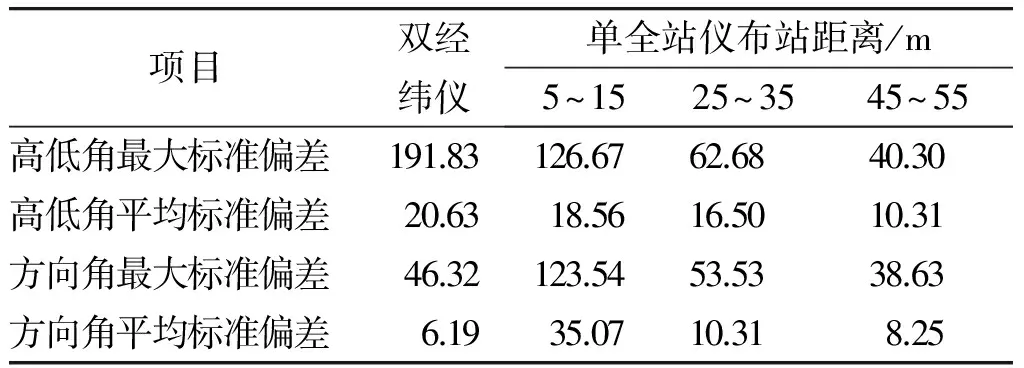
表2 两种测量系统不确定度仿真结果分析 (″)

3 测量系统工作效率

对双经纬仪调炮精度测量系统和单全站仪调炮精度测量系统工作过程进行分析，表3是对两种系统分别测量1次调炮精度耗费时间的统计(假设操作员的熟练程度一样，现场情况一致，操作满足精度要求,不计调炮时间及准备工作时间)。单全站仪调炮精度测量系统操作工作量不足双经纬仪系统的一半，极大简化了操作，一定程度上提高了测量效率。

表3 两种测量系统工作操作量统计 min

4 结束语

在仿真计算的基础上，对双经纬仪调炮精度测量系统和单全站仪调炮精度测量系统进行了基于蒙特卡洛法不确定度分析。通过比较分析可知，单全站仪调炮精度测量系统在满足布站距离要求时，其测量精度优于双经纬仪调炮精度测量系统，且单全站仪测量方法操作简单方便，可作为调炮精度测量方法的首选。

References)

[1]方安国，徐锐，张金萍.火箭炮调炮精度的几种测量方法比较研究[J].火炮发射与控制学报，2013(3):76- 79. FANG Anguo，XU Rui，ZHANG Jinping.The comparison study on several survey method of rocket launcher’s adjustment accuracy[J].Journal of Gun Launch & Control,2013(3):76-79.(in Chinese)

[2]罗鸿飞，张英堂，任国全，等.基于空间坐标解算的火炮调炮精度检测方法研究[J]．火炮发射与控制学报，2007(3)：50-52． LUO Hongfei，ZHANG Yingtang，REN Guoquan，et a1．Research on measuring method of gun rotated accuracy based on spatial coordinate algorithm[J]．Journal of Gun Launch & Control，2007(3)：50-52．(in Chinese)

[3]曾刊,赖文娟,雷雨能. 单全站仪调炮精度检测系统[J]. 四川兵工学报,2013,34(4):18-19，28. ZENG Kan,LAI Wenjuan,LEI Yuneng.Gun slaving accuracy measurement system based on total station apparatus[J].Journal of Sichuan Ordnance,2013,34(4):18-19，28. (in Chinese)

[4]刘存成,胡畅.基于MATLAB用蒙特卡洛法评定测量不确定度[M].北京：中国质检出版社和中国标准出版社，2014. LIU Cuncheng，HU Chang. Evaluate uncertainty of mea-surement based on MATLAB with Monte Carlo method[M].Beijing:China Zhijian Publishing House and China Standard Press，2014. (in Chinese)

[5]杨凡,娄妍,孙现申,等.现代精密工程测量技术及仪器[J].测绘科学,2011,36(3):44-46. YANG Fan，LOU Yan，SUN Xianshen，et al. Technology and instruments of precise engineering surveying[J].Scie-nce of Surveying and Mapping,2011,36(3):44-46. (in Chinese)

Research on Uncertainty of Gun Slaving Accuracy Measurement Systemwith One Total Station Based on Monte Carlo Method

LIU Zhipeng1，LI Kai2，XU Qiang1

(1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China;2.Hubei Jiangshan Heavy Industries Co.,LTD,Xiangyang 441057,Hubei,China)

For the purposes of improving gun slaving accuracy measurement system, the mathematical model is to be conducted through gun slaving accuracy measurement systems with one total station, which is to be used to correct the main factors in affecting the measurement precision in the process of measurement. MATLAB based on Monte Carlo method is to be used to simulate and analyze the uncertainty of the gun slaving accuracy measurement system. The simulation results indicate that when total station measurement system meets the distance requirement, its accuracy is higher than that of double theodolite measurement system with the workload of the system of one total station being half of that of double theodolite system, which simplifies the operation and improves the working efficiency, posse-ssing good application value in the measurement of gun slaving accuracy measurement system.

engineering survey technology; gun rotated accuracy; Monte Carlo method; uncertainty; total station;double theodolite

2016-03-16

刘志鹏(1991—), 男, 硕士研究生，主要从事武器系统测试测量技术研究。E-mail：lzp208319@126.com

10.19323/j.issn.1673- 6524.2017.02.014

TJ393

A

1673-6524(2017)02-0063-04