基于IDEA模型的坦克性能指标需求方案有效性分析

徐亚军，侯胜高，肖慧鑫

（1.装甲兵学院，安徽 蚌埠 233050；2.中部战区政治工作部，北京 100144）

基于IDEA模型的坦克性能指标需求方案有效性分析

徐亚军1，侯胜高1，肖慧鑫2

（1.装甲兵学院，安徽 蚌埠 233050；2.中部战区政治工作部，北京 100144）

针对坦克车辆性能指标需求方案有效性分析的输入指标为区间数、具有模糊性这一实际情况，提出了一种基于IDEA模型的需求方案有效性分析方法，并详细给出了该方法的计算步骤和算法。研究表明，该方法能够有效完成需求方案的有效性分析，同时也简化了计算过程，使得分析结果更为客观合理，最后通过一个示例来验证模型的可行性和有效性。

IDEA模型，需求方案，有效性分析

0 引言

坦克性能指标需求方案的有效性分析是坦克车辆发展论证的重要环节，有效性分析的结论不仅能够为需求方案的分析决策提供一定的参考，同时它也是优化方案发展资源的重要依据之一。如果需求方案的有效性缺乏科学的分析，在后期的研制阶段将会造成一定的资源浪费，因此，必须对坦克车辆性能指标需求方案的有效性进行科学合理的分析。

到目前为止，笔者尚未检索到有关坦克车辆性能指标需求方案有效性分析的直接研究成果。但通过研究，发现坦克车辆性能指标需求方案的有效性分析属于一个多输入、多输出的决策问题，针对这样一个多输入、多输出的决策问题，DEA（数据包络分析）是一种比较有效的分析方法。同时，为了解决坦克车辆性能指标需求方案的输入指标在论证阶段不可能通过分析计算得出一个准确的数值，只能根据类似装备的研制和使用数据，运用科学的方法并结合专家的意见预测得出一个相对准确的区间范围这一问题，本文引入IDEA（区间数据包络分析）模型，力求为坦克车辆性能指标需求方案有效性分析提供一条有效的途径。

1 IDEA模型

假设有n个坦克车辆性能指标需求方案，这n个性能指标需求方案都具有可比性，每个性能指标需求方案有m种类型的输入和s种类型的输出，每种输入和输出都是一个以区间数形式表示的模糊数，它们可以用向量的形式表示为：

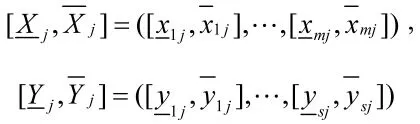
原有的效率评价指数转化为下面的区间效率评价指数：

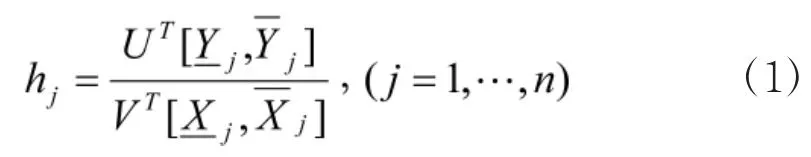
hj是一个区间数，表示为：

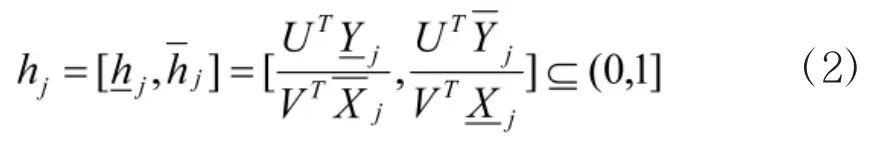
其中V，U分别表示输入、输出指标的权重向量，可以选择适当的V，U，使得hj≤1。因此，第j0个决策单元的区间效率评价指数可由下面的分式规划模型的最优值来确定。

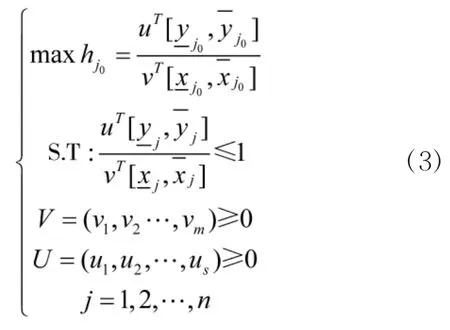
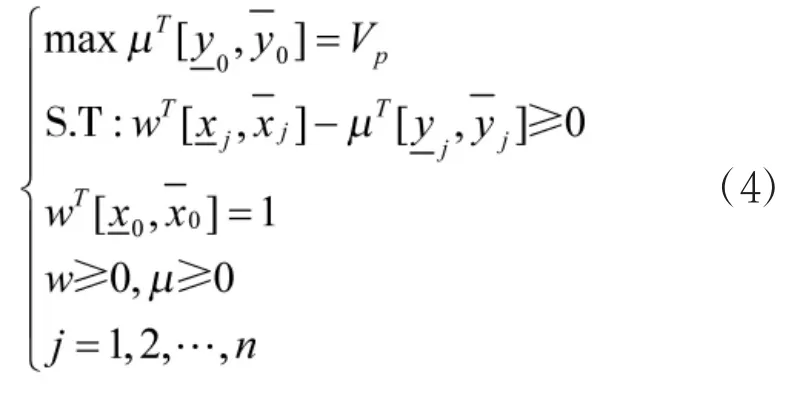
根据线形规划的对偶理论，可以得到上述线形规划模型的对偶模型：

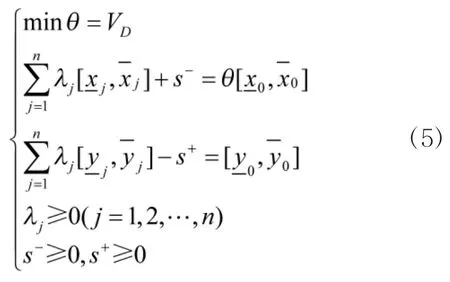
上述对偶模型的计算过程可以分为以下两种情况：

①正被分析的坦克车辆性能指标需求方案的输入值取区间的最小点，输出值取区间的最大点，其他坦克车辆性能指标需求方案的输入值取区间的最大点，输出值取区间的最小点，这时利用该对偶模型计算出的有效性系数为有效性系数区间的

②正被分析的坦克车辆性能指标需求方案的输入值取区间的最大点，输出值取区间的最小点，其他坦克车辆性能指标需求方案的输入值取区间的最小点，输出值取区间的最大点，这时利用上述对偶模型计算出的有效性系数为有效性系数区间的最小点，记作。

2 有效性分析的基本步骤

2.1 输入、输出指标的确定

要想使用IDEA模型对坦克车辆性能指标需求方案进行有效性分析，首先需要给出需求方案的输入、输出指标。坦克车辆性能指标需求方案有效性分析的输入指标是指提高坦克性能指标需要投入的要素，一般包括坦克的研制费用、采购费用、使用维修费用、研制时间等。而有效性分析的输出指标通常是一些收益性的指标，对坦克车辆性能指标需求方案而言，它直接表现为各种性能指标的提高值，一般包括火力性能提高值、机动性能提高值、防护性能提高值、通信指挥性能提高值、可靠性及维修性提高值以及人机环境适应性提高值等。

2.2 输入、输出指标的计算

输入指标通常是一些投入性的指标，仅仅根据坦克车辆性能指标需求方案不能准确地计算出它们的数值，只有根据需求方案制定出相应的研制方案后，并通过对类似装备研制使用数据的分析，运用一定的数学方法才能预测得出，本文对各个输入指标的计算方法就不一一介绍。输出指标是坦克性能指标的提高值，即新的性能指数与原有的性能指数的差值，可以采用幂指数法来计算性能指数，然后将新的性能指数减去原有的性能指数，即可得到方案的输出指标。

2.3 有效性的计算

在计算出需求方案有效性分析的输入、输出指标之后，选择IDEA模型分别建立各个需求方案有效性分析的对偶模型，然后利用软件LINGO7.0对各个方案的对偶模型进行求解计算。

2.4 有效性分析的结论

坦克车辆性能指标需求方案通常按照区间有效、区间部分有效、区间无效的次序进行排序，但有时也存在以下3种情况需要分析比较之后才能作出最终的排序。

①当方案A1、A2同为区间有效时，采用以下模型计算的超效率的下限值

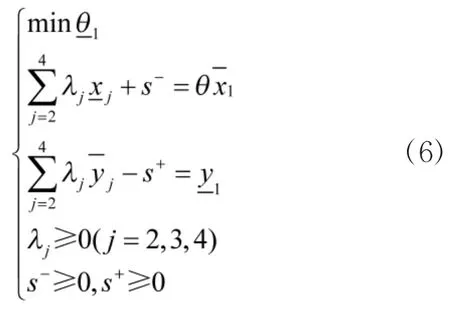
同理，计算方案A2的超效率的下限值比较和的大小，即可对方案A1和A2进行排序，若则方案A1优于A2，反之，方案A2优于A1。

②当方案A3、A4同为区间部分有效时，比较方案A3和A4有效性系数区间的下限值即可对它们进行排序，若，则方案A3优于A4，反之，方案A4优于A3。

③当方案A5、A6同为区间无效时，比较方案A5和A6有效性系数区间的下限值即可对它们进行排序，若，则方案A5优于A6，反之，方案A6优于A5。

3 某型坦克性能指标需求方案有效性分析

下面，在某型主战坦克性能指标的基础上，结合国内外各型主战坦克的相关知识，拟定出4个坦克性能指标需求方案，如表1～表4所示。

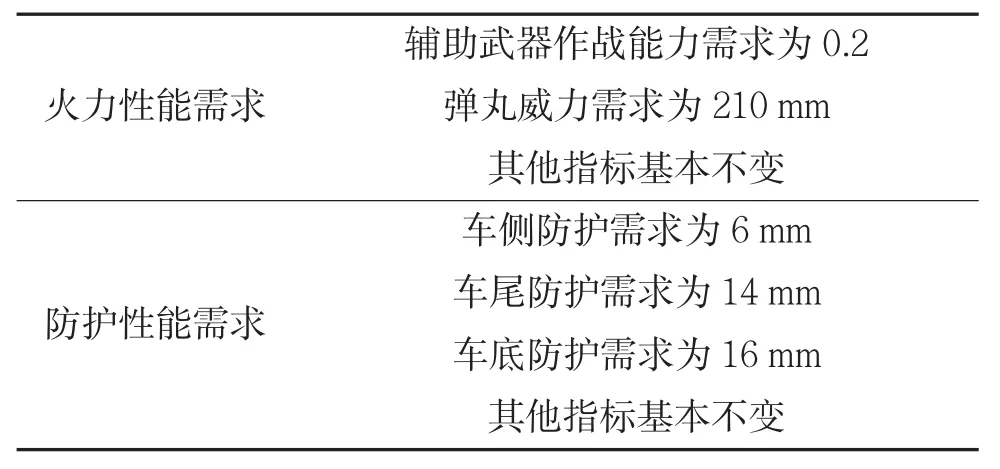
表1 某型坦克性能指标需求方案A

表2 某型坦克性能指标需求方案B

表3 某型坦克性能指标需求方案C

表4 某型坦克性能指标需求方案D

结合这4个需求方案可以拟制确定各个需求方案对应的研制方案，并根据研制方案计算出各个需求方案有效性分析的输入和输出性指标如表5所示：

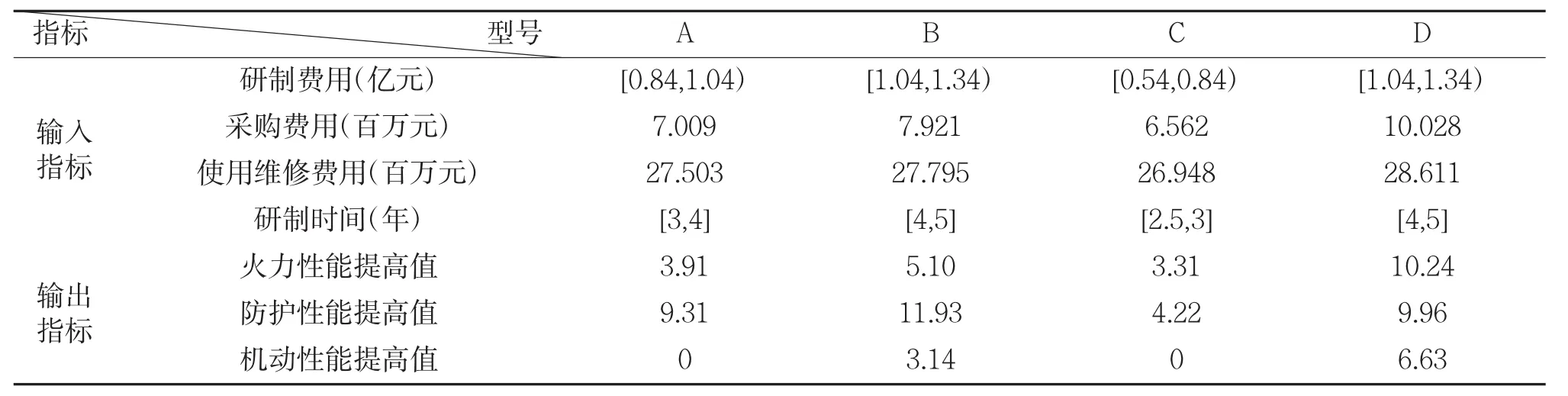
表5 各方案有效性分析的输入、输出指标值

首先，运用IDEA模型对上述4个方案的有效性进行分析，建立方案A的IDEA模型：

同理，可以建立方案B、C、D的IDEA模型，利用线形规划软件LINGO7.0计算各个方案IDEA模型的解及相关信息如表6：

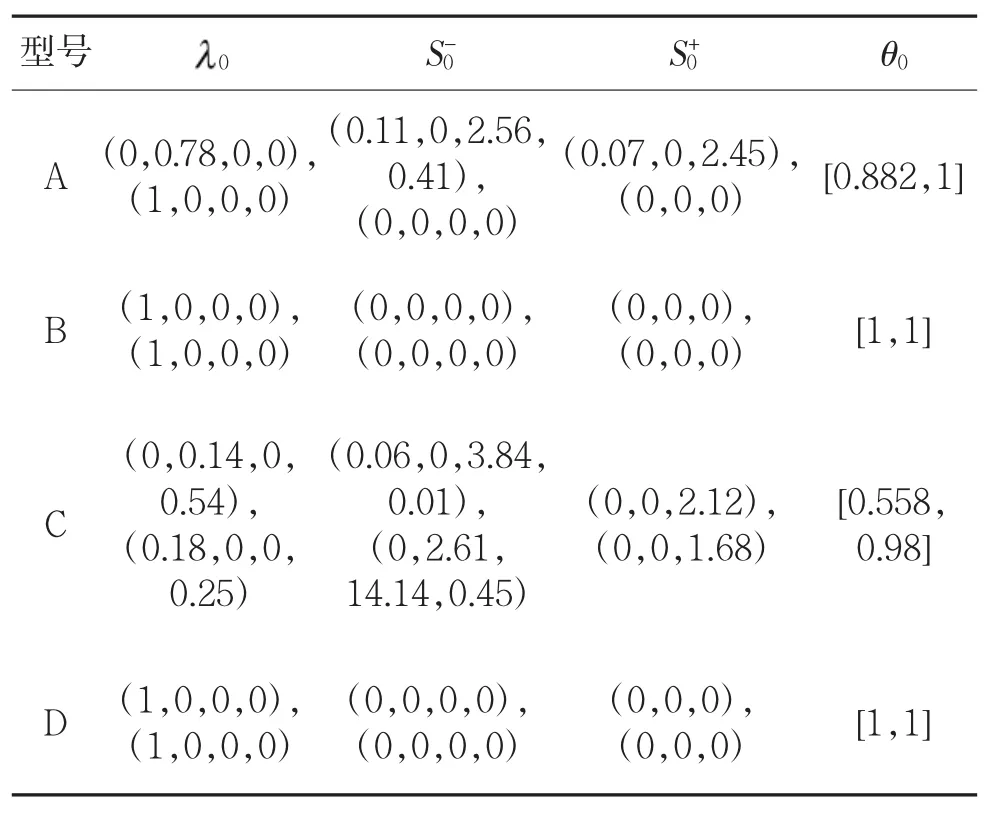
表6 各方案IDEA模型的解及相关信息

从表中可以看出，方案B和D同为区间有效，为了能够进一步区分方案B和D，下面利用式（6）对它们进行分析比较。

建立方案B的SE-IDEA模型：

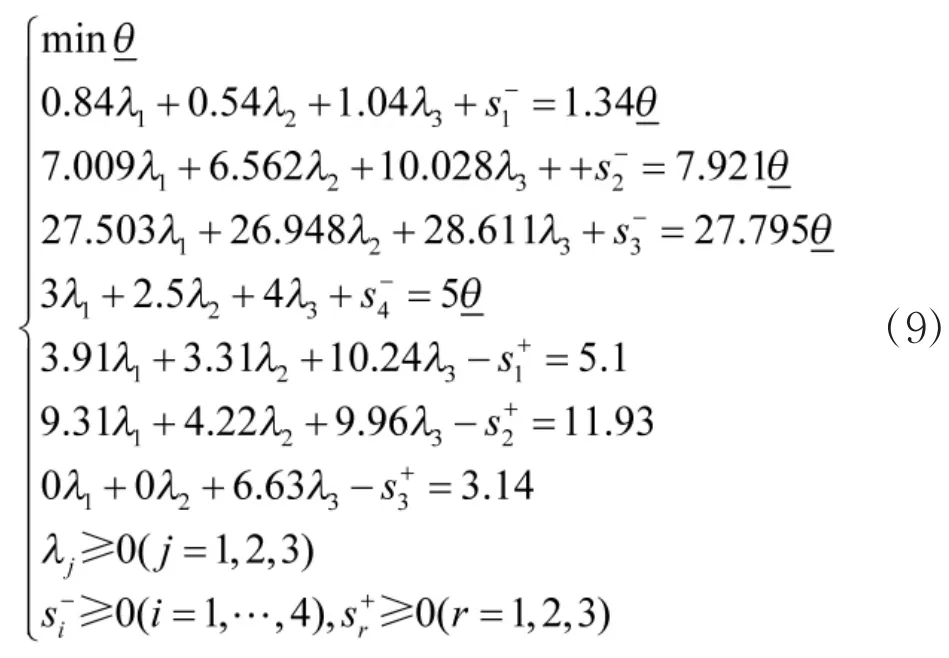
同理，可以建立方案D的SE-IDEA模型，利用线形规划软件LINGO7.0计算上述两个模型的解及相关信息如表7：

表7 B、D方案SE-IDEA模型的解及相关信息

从表中可以看出，方案B的有效值为1.285，方案D的有效值为2.051，因此，方案D比方案B更为有效。方案A为区间部分有效方案，方案C为区间无效方案。因此，4个方案的最终排序为：方案D>方案B>方案A>方案C。

4 结论

通过以上分析可以发现，基于IDEA模型的坦克性能指标需求方案有效性分析，能够有效解决输入指标和输出指标是区间数、带有模糊性这一问题。同时，本文还给出了方案有效性的排序方法，并对排序的具体计算过程作了简化分析，为当前坦克性能指标需求方案的有效性分析提供了一条有效途径。

［1］魏权龄.数据包络分析［M］.北京：科学出版社，2004.

［2］安会刚.带偏好的区间DEA模型及其应用［J］.工业工程，2007，10（2）：33-36.

［3］安会刚.航空武器项目区间DEA评价与决策［J］.航空计算技术，2006，36（1）：12-15.

［4］郭均鹏.区间超效率DEA模型及其应用［J］.佳木斯大学学报，2006，24（1）：19-21.

［5］郭均鹏.区间数据包络分析的决策单元评价［J］.系统工程理论方法应用，2004，27（3）：89-93.

Validity Analysis of Tank Performance Index Requirement Project Based on IDEA Model

XU Ya-jun1，HOU Sheng-gao1，XIAO Hui-xin2
（1.Amored Corps Institute，Bengbu 233050，China；2.Political Work Department of Centrnal Theater Command，Beijing 100144，China）

Aiming at the problem of tank performance index requirement project validity analysis which inputs indexs are fuzzy，this article proposes a validity analysis method of index requirement project based on IDEA model，then，giving the calculation steps and methods in detail.Studying shows that this method can complete the requirement project validity analysis effectively.Also，it does some improvement on the calculate process，making the analysis result more impersonality.Finally，this article gives an example to show the feasibility and effectiveness of the model.

IDEA model，requirement project，validity analysis

TJ015

A

1002-0640（2017）05-0099-04

2016-03-05

2016-05-07

徐亚军（1986- ），男，江苏扬中人，硕士。研究方向：装甲装备发展与系统工程。