基于灰色加权马尔科夫的部队集成训练效果预测*

蔡艳军，赵 睿

（武警工程大学，西安 710086）

基于灰色加权马尔科夫的部队集成训练效果预测*

蔡艳军，赵 睿

（武警工程大学，西安 710086）

针对GM（1，1）预测模型误差较大的问题，在GM（1，1）模型的基础上引入加权马尔科夫模型构建了部队集成训练效果预测模型。该模型以GM（1，1）模型存在的预测残差作为划分马尔科夫状态的依据，通过加权处理对预测结果进行修正。实例分析结果表明，该模型算法简单，易于实现，可以较大地提高部队训练效果预测精度，为部队开展科学有效的实战化训练提供了有力的数据支撑。

信息系统，集成训练，效果预测

0 引言

训练考核成绩是衡量部队训练效果的重要指标。当前，在部队训练效果评估研究和运用方面，主要有模糊评判法、云理论、层次分析法等［1-4］，这些方法主要关注的是对静态训练效果的评估。然而，基于信息系统集成训练作为提高部队战斗力的重要手段，其过程是动态、可持续的，其训练效果也是实时、动态的，而且能够反映训练发展变化的总趋势。因此，部队开展集成训练效果研究，不仅要关注训练效果，更要注重考察各阶段训练效果的发展变化情况，通过对训练效果进行预测来反思当前部队训练存在的问题，为科学组训提供数据支撑。

基于此，本文构建了基于灰色加权马尔科夫的部队集成训练效果预测模型。该模型在GM（1，1）模型基础上，引入马尔科夫状态转移模型，并对预测状态概率进行加权，算法简单、易于实现、准确度高。其基本思路是：根据原始样本数据（实际考核成绩），利用GM（1，1）取得部队集成训练效果预测成绩与样本数据之间的残差值，作为划分马尔科夫状态的依据，建立马尔科夫状态转移矩阵，对各状态分布概率作加权处理，以此来修正GM（1，1）模型的预测误差，提高预测精度。

1 建立GM（1，1）预测模型

GM（1，1）模型即灰色模型（Grey Model），是灰色预测理论的经典模型，适用性强。由文献［5］可知，GM（1，1）模型的原始形式为：

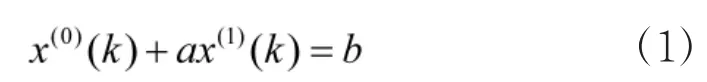
GM（1，1）模型的基本形式为：

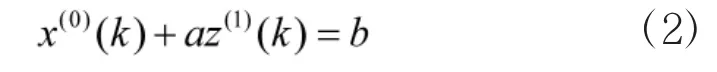
GM（1，1）模型的关键就是求解a和b值。为了方便求解a和b的值，将GM（1，1）模型改写为矩阵方程：Y=B·A。

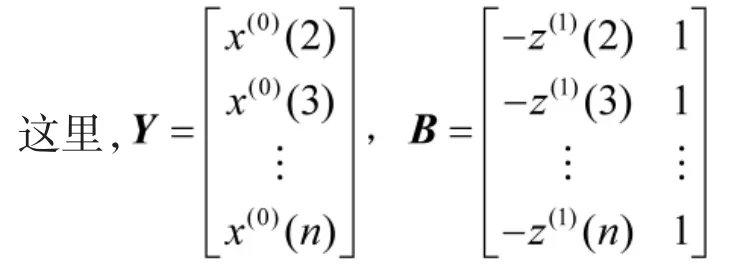
利用最小二乘法计算a和b的参数估计值，即：

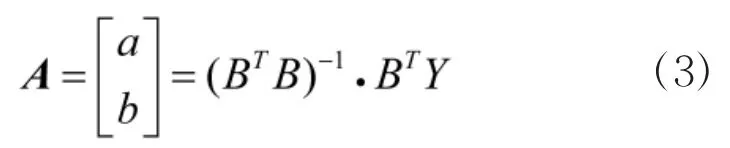
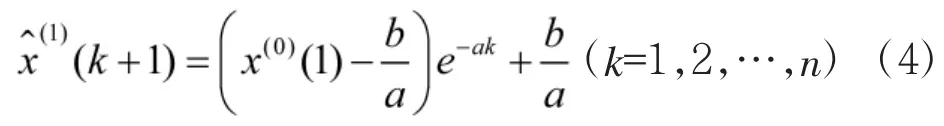
进行累加还原后，其原始数据序列的灰色预测模型为：

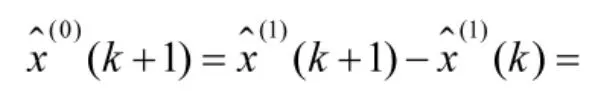
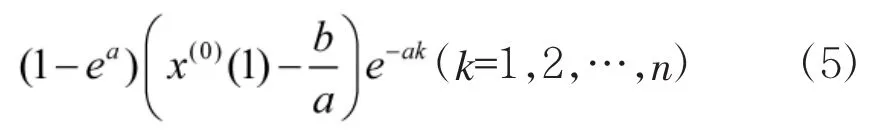
本文选取某部上一年度1月～12月集成训练月考成绩作为样本数据，该成绩依据相关要求《训练与考核大纲》考核得来。为了获得精度较高的GM（1，1）模型，需要对原始数据序列的数据级比进行检验［6］，即数据级比σ（k）必须满足。样本数据及级比验证结果如表1所示。

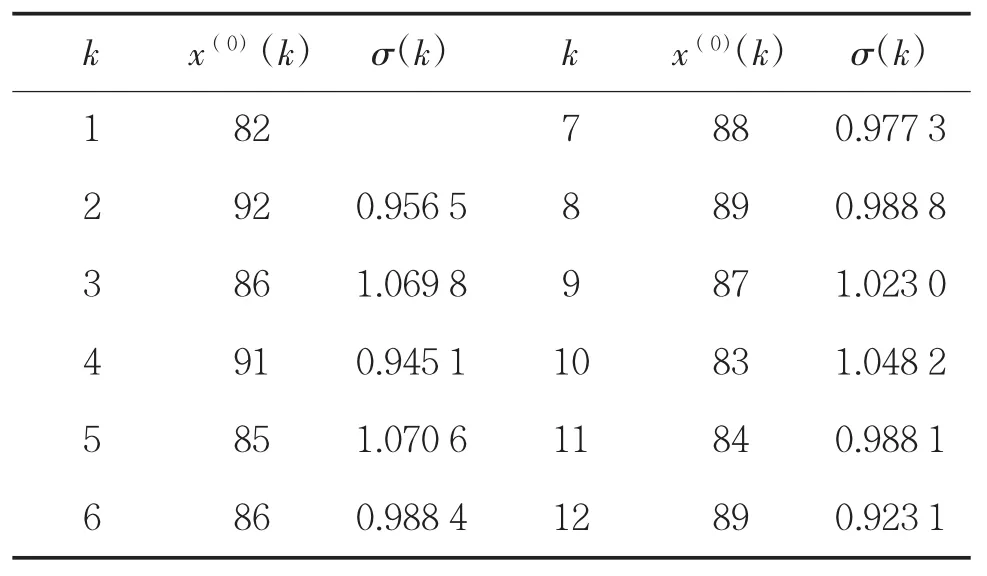
表1 样本数据及级比

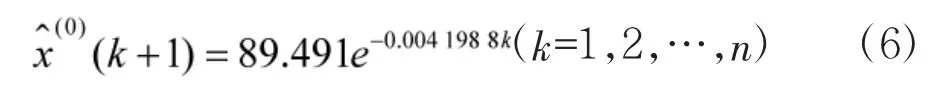
由式（6）计算可得该部上一年度1月～11月基于GM（1，1）模型的集成训练考核预测成绩，如表2所示。

表2 GM（1，1）模型预测结果

2 加权马尔科夫修正模型

由表2所示，对比样本数据和GM（1，1）模型预测结果，可以发现预测结果与实际值之间的误差较大。为了提高预测精度，引入加权马尔科夫修正模型，对预测值误差进行修正。在这里，以该部1月～ 11月基于GM（1，1）模型预测成绩与实际成绩的残差作为划分马尔科夫状态的依据，对误差进行修正。在此基础上，通过数据分析对比，验证所建预测模型的有效性。

2.1 划分状态转移区间

定义δ（k）为残差，ε（k）为相对残差，其中：

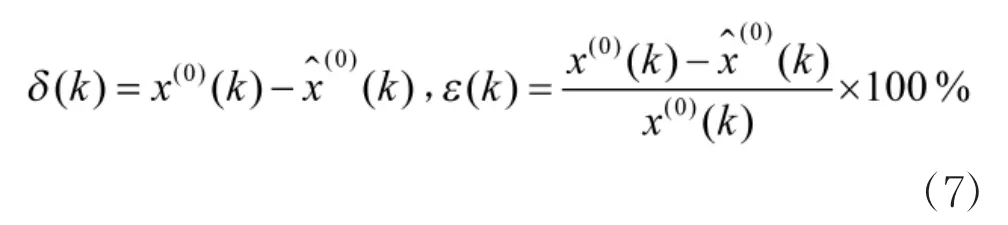
根据式（7），计算得出表2中基于GM（1，1）模型的预测成绩与实际训练成绩的残差值δ（k）和相对残差值ε（k），根据残差分布情况，将其划分5个状态区间，分别是：E1=（-4，-2），E2=［-2，0），E3=［0，2），E4=［2，4），E5=［4，∞）。由此，每个残差所处的状态分布如表3所示。

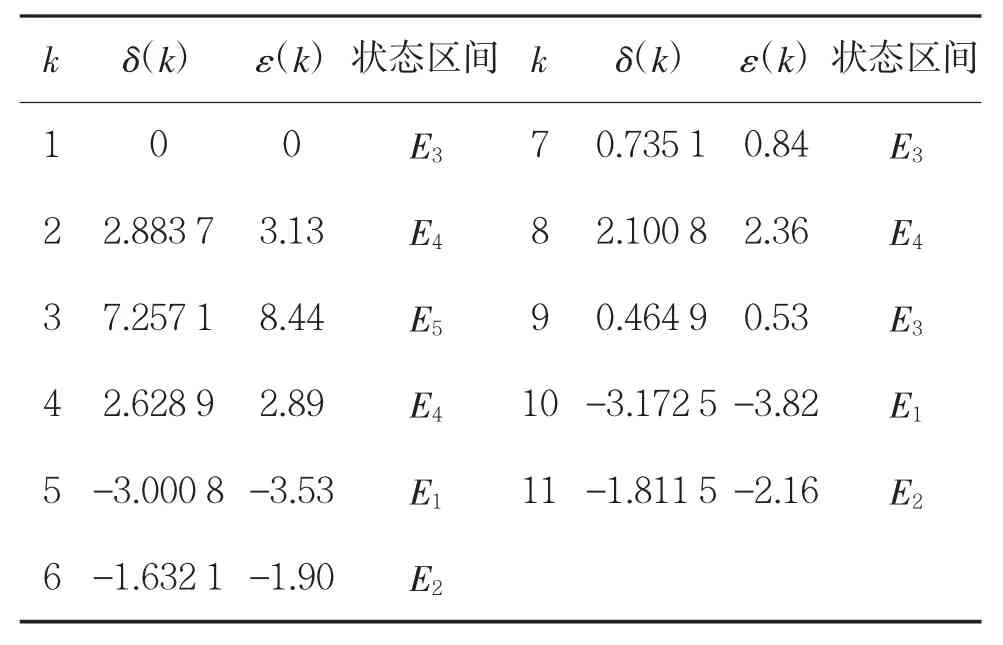
表3 残差状态分布

2.2 建立状态转移矩阵

根据表3中残差分布情况，构建s步马尔科夫状态转移概率矩阵为：

2.3 确立各阶权值

运用马尔科夫模型修正预测结果时，要考虑各状态之间的强弱关系，即各阶（转移步长）马尔科夫的绝对分布在预测中所起的作用。在这里，用权重值ws即各步长样本的自相关系数来反映各状态之间的关系。ws计算方式如下［7］：

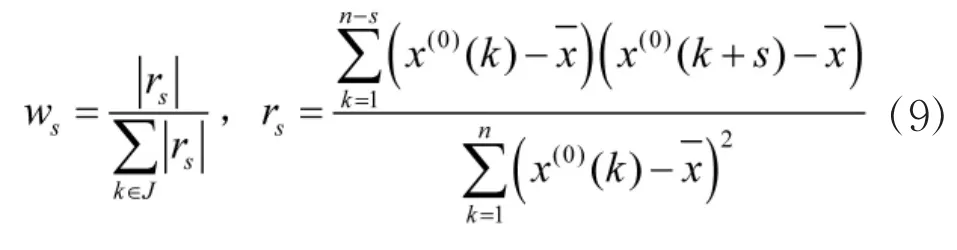
式中，rs表示各阶自相关系数，x軃表示样本数据序列的均值，对各阶自相关系数进行归一化处理即可得到各阶权重ws。对不同步长的转移概率加权，即：。式中，pj为第j种预测状态的概率；为第k阶第j种预测状态的概率。

由式（9）计算可得各阶状态转移权重值：w=［w1w2w3w4］=［0.051 8，0.000 7，0.527 2，0.420 3］。选取与12月最近的8月～11月训练考核成绩所在的区间状态为初始状态，分别计算出转移步数为4、3、2、1步的结果，并对其加权求和来确定12月训练考核成绩的预测值。计算结果如表4所示。

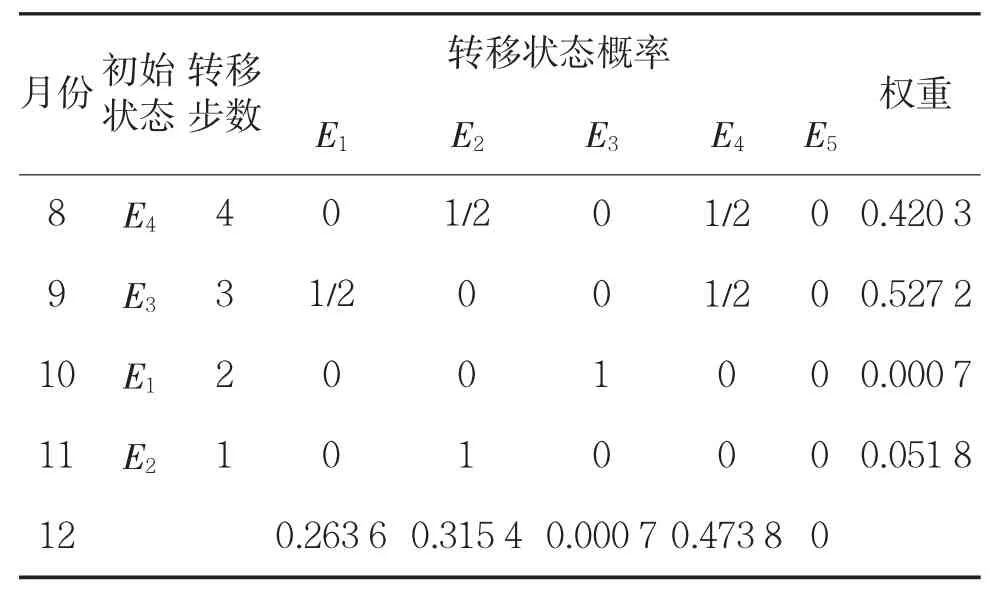
表4 加权权重值计算结果

2.4 修正预测结果

选择最大加权权重值作为预测未来状态的依据，确定预测值的变化区间。由表4可知，12月训练成绩预测值的残差处于状态E4的可能性最大，从而可预测该部12月份训练考核成绩的残差修正值Q为：

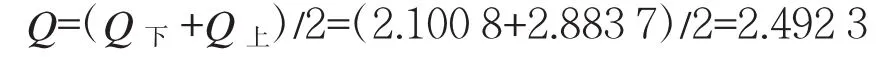
这里选取Q下、Q上为该状态区间中残差最小值、最大值作为状态区间E4的下限值和上限值，即Q下=2.100 8，Q上=2.883 7，并据此计算残差修正值。最终预测结果为：

3 结论分析

表5给出了该部12月份集成训练考核成绩预测结果分析。从表中可以看出，在原有GM（1，1）预测模型基础上，引入加权马尔科夫模型对其预测误差进行修正，其预测精度提高了3倍。

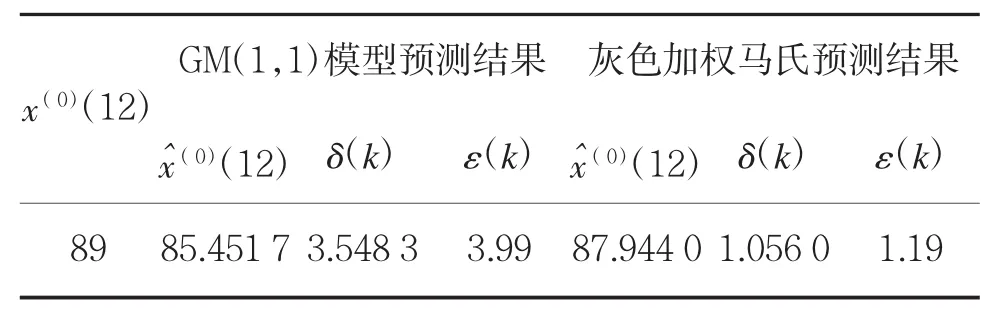
表5 结果对比

由此可见，运用灰色加权马尔科夫预测模型对部队集成训练成绩进行预测，克服了训练成绩因各种因素随机波动较大对预测结果的影响，预测精度高，计算简单，便于实现，这些都可以有力促进基于信息系统实战化集成训练。同时，在预测过程中，通过对部队训练成绩数据在各个状态上的分析研究，可以对部队训练效果实施有效评估，有利于帮助指挥员协调、控制部队训练过程，改进训练方法，为部队科学训练、针对性训练提供了有力的数据支撑。

［1］郑敏娇，郑安卡，李文元.基于改进模糊综合评判的指挥信息系统对抗训练效果评估［J］.微电子学与计算机，2014，（5）：179-183.

［2］崔凯旋，石全，张文宇，等.云理论在装备保障训练效果评估中的应用［J］.火力与指挥控制，2013，38（3）：108-111.

［3］徐池，石宁权，黄晓飞.舰艇通信兵训练效果评估研究［J］.指挥控制与仿真，2011，33（1）：74-77.

［4］冯鑫，危懿.基于AHP与模糊综合批判的模拟训练效果评估研究［J］.重庆通信学院学报，2015，34（4）：43-46.

［5］刘思峰，党耀国，方志耕，等.灰色系统理论及其应用［M］.北京：科学出版社，2004：125-134.

［6］彭勇.基于灰色马尔科夫理论的体能训练效果预测与评价模型［J］.军事运筹与系统工程，2013，27（3）：59-61.

［7］王铁宁，朱域，陈晓晨.基于灰色加权马尔科夫的备件需求预测［J］.装甲兵工程学院学报，2015，29（3）：8-13.

Research on Integrated Training Effect Prediction of Troops Based on Gray Weighted Markov Model

CAI Yan-jun，ZHAO Rui
（Engineering University of Chinese Armed Police Force，Xi’an 710086，China）

Aiming at the error of GM（1，1）prediction model，the integrated training effect prediction model is established by using the weighted Markov method based on GM（1，1）model in this paper.In this model，the Markov state is dividing on the errors in GM（1，1）model，and then the prediction result is improved by using the weighted Markov method.The example result analysis shows that the algorithm of this model is more simpler，and the training effect prediction veracity is more accurate，and this model can provide the powerful date support for battle-focused training.

information system，integrated training，effect prediction

E13

A

1002-0640（2017）05-0023-03

2016-04-06

2016-05-07

全军军事学研究生基金资助项目（JYKTXS1404）

蔡艳军（1983- ），男，湖北武汉人，博士研究生，讲师。研究方向：军事通信。