边缘化粒子概率假设密度滤波的多目标跟踪*

于 洋，宋建辉，刘砚菊，司冠楠

（沈阳理工大学自动化与电气工程学院，沈阳 110159）

边缘化粒子概率假设密度滤波的多目标跟踪*

于 洋，宋建辉，刘砚菊，司冠楠

（沈阳理工大学自动化与电气工程学院，沈阳 110159）

针对复杂情况下的多目标跟踪问题，提出一种边缘化粒子概率假设密度滤波（MPF-PHD）方法。该方法首先将复杂情况下多个目标的状态向量分别提取出其中的非线性状态与线性状态。然后利用粒子概率假设密度滤波（PF-PHD）估计非线性状态，利用卡尔曼滤波（KF）估计线性状态，并把其中与非线性状态相关的线性状态估计用来优化非线性状态估计。通过对MPF-PHD方法与传统的PF-PHD方法仿真对比，验证了MPF-PHD方法有效解决了复杂情况下多目标跟踪的漏检问题，提高了多目标状态估计精度。

边缘化粒子概率假设密度滤波，多目标跟踪，非线性状态估计，卡尔曼滤波

0 引言

目标跟踪问题依据被跟踪目标数目可分为单目标跟踪与多目标跟踪。单目标跟踪只需区分出目标与杂波，而多目标跟踪不仅要区分出杂波干扰，还要获知跟踪区域内的目标数目以及传感器量测来源于哪个目标。因而这就不得不涉及到传统的“关联-估计”的多目标跟踪方法，如联合概率数据关联（jointprobabilisticdataassociation，JPDA）［1］算法，多假设跟踪（multiplehypothesistracking，MHT）［2］等，结合贝叶斯滤波框架下的传统状态估计滤波方法实现对多个目标的跟踪。然而，由于跟踪区域中目标的产生、消亡是随机的，因此，目标的状态与数目是时变的。这种情形会导致传统的基于数据关联的多目标跟踪方法数据关联精度较低，将直接影响到之后的目标状态估计的效果，并且随着目标数目的增加还会出现计算量成指数增长的问题。针对这样的多目标跟踪问题，应当采用一种能体现出跟踪区域内这种随机变化性的状态估计滤波方法。因此，由Mahler首次将随机有限集（random finite set，RFS）用作对多目标状态以及传感器量测的描述。基于贝叶斯滤波框架，采用随机有限集描述的多目标跟踪会因为多目标状态空间上的多维积分而导致计算量过大。因而，基于RFS的概率假设密度（probability hypothesis density，PHD）［3］滤波算法应运而生。PHD滤波将多目标状态集合的后验概率密度在单目标状态空间上作了智能近似，避免了复杂的数据关联，从而降低了计算复杂度。由于PHD滤波算法递推公式中存在多个积分运算，难以得到其解析解，因而文献［4］又给出了一种高斯混合（Gaussian Mixtrue，GM）的实现方法。在GM-PHD滤波过程中，一系列加权高斯成分用来估计多目标状态集合后验概率密度的一阶统计量，并对高斯混合项进行修剪，使高斯混合项的数量维持在合理的范围内，保证对多目标数目和状态持续有效的估计。

实际情形中，复杂情况下的多目标跟踪系统的量测噪声会因为目标弱小、近距离运动而表现出非高斯特性，同时如果目标处于机动运动状态，则被跟踪的目标状态向量会包含有非线性元素［5-8］。针对这种非线性非高斯的多目标跟踪系统，由文献［9］给出一种序贯蒙特卡罗概率假设密度（SMC-PHD）滤波方法，即基于粒子滤波的概率假设密度（PF-PHD）滤波方法。该方法基于序贯重要性采样的随机样本，并赋以权值来对PHD函数进行逼近。但实际应用时，状态维数通常高于量测维数，需要大量采样粒子保证状态估计性能［10］。因而，基于边缘化粒子滤波（MPF）的思想，结合PHD状态估计，提出一种边缘化粒子概率假设密度（MPF-PHD）状态估计滤波方法实现复杂情况下的多目标跟踪。该方法将状态向量划分为非线性与线性两部分，通常以目标位置等信息为非线性状态，目标速度与加速度等信息为线性状态。非线性状态采用PF-PHD状态估计滤波，线性状态采用线性条件下最优的状态估计，即卡尔曼滤波（KF）［11-14］。结合目标动态运动模型，部分线性状态与非线性状态存在相关性，而这种相关性可以用来优化非线性状态估计。

1 PHD滤波

基于RFS理论的PHD，根据其定义就是指多目标后验概率密度分布的第一阶矩，PHD滤波利用后验概率密度分布的第一阶矩来代替RFS递推过程中的多目标的后验概率密度，降低了多目标跟踪算法的难度和复杂度。记为传感器从1到k-1时刻的累积测量序列，则PHD滤波的预测和更新公式如式（1）、式（2）：

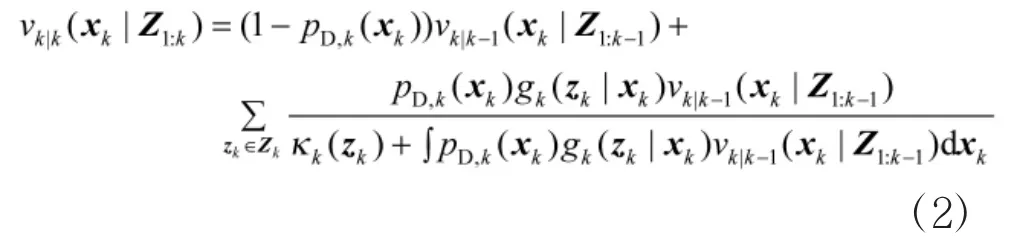
2 复杂情况下多目标跟踪MPF-PHD方法的实现

2.1 模型描述

多目标跟踪系统中的状态向量可分为非线性部分与线性部分，其中线性部分又与非线性部分相关联。设为k时刻非线性状态子向量，为k时刻线性状态子向量，与共同构成完整的状态向量，F与G分别代表状态转移矩阵与噪声转移矩阵。那么跟踪区域中多个目标状态的动态模型有如下表示：

同时，传感器量测模型可以表示为：

其中，ek为零均值高斯白噪声。

将系统描述为线性高斯的，则不考虑非线性状态，只需考虑式（4）所表示线性状态模型，并利用KF对线性状态估计，同时式（6）可表示为：

针对系统存在的非线性状态，运用PF-PHD方法估计状态。设截止到k-1时刻的非线性状态随机集为，k时刻非线性状态为则根据式（3）所表示的非线性状态模型，可以推得如下表示：

其中，Rn表示如下：

2.2 MPF-PHD方法步骤

依据边缘化粒子滤波的思想与多目标跟踪的PHD状态估计方法，结合复杂情况下多目标跟踪的模型描述。

MPF-PHD方法分为4个步骤，流程图如图1所示：

图1 MPF-PHD算法流程图

下面以伪代码形式给出MPF-PHD的算法实现流程：

2.2.1 初始化

设N0为0时刻目标数，为0时刻的估计目标数，状态随机集初始粒子为，权值为

2.2.2 预测

假设传感器检测概率pD，k与目标存活概率pS，k相互独立，k-1时刻的PHD为：

对目标进行非线性状态粒子预测，根据式（8）可得：

对粒子权值的预测，分别针对存活目标、衍生目标、新生目标有如下表示。

2.2.3 更新

在得到k时刻量测集之后，需要更新粒子权值并给出k时刻的PHD估计：

其中权值根据式（2），更新为

2.2.4 重采样

通过上述4个步骤的递推，可以得到带权值的粒子集来表征k时刻的PHD。k时刻的PHD是一个多峰的函数，峰的个数代表估计的目标数目，由上述k时刻所有权值和来表征：

多峰函数中峰的位置指代多目标的状态的估计。

由上述多目标跟踪模型以及MPF-PHD状态估计过程可知，复杂情况下的非线性状态估计过程包含有线性状态成分，此线性状态信息用来优化估计非线性成分。由此可以看出，相对于PF-PHD状态估计方法，MPF-PHD方法进行了合理的改进，将多目标状态划分为非线性与线性两部分进行处理，极大地提高了目标数目与目标状态跟踪精度，减少了目标漏检现象的发生。

3 仿真结果与分析

假定一个在复杂杂波情况下，目标数目未知且时变的二维多目标运动场景。设k时刻目标真实个数为Nk，记第个目标状态向量为，其中，表示水平面笛卡尔坐标，表示目标速度。

同时令监控时间长度为40 s，传感器采样间隔T=1 s，则目标状态转移矩阵和其状态噪声转移矩阵设为：

基于上述场景，传感器目标检测概率pD，k设为0.95，同时设目标存活概率pS，k为0.99。设传感器位于坐标原点且可获取目标距离和角度测量。

本系统设定仿真场景中，目标1产生于1 s，消亡于7 s；目标2由目标1产生，产生于8 s，消亡于25 s；目标3产生于12 s，消亡于37 s；由目标2衍生出的目标4，产生于26 s消亡于40 s。观测范围内产生均匀分布的服从泊松过程模型的杂波信号。根据上述目标场景，以目标位置信息为非线性状态，以目标速度为线性状态。非线性状态采用PF-PHD状态估计滤波，线性状态采用线性条件下最优的状态估计，即KF。仿真结果如图2所示：

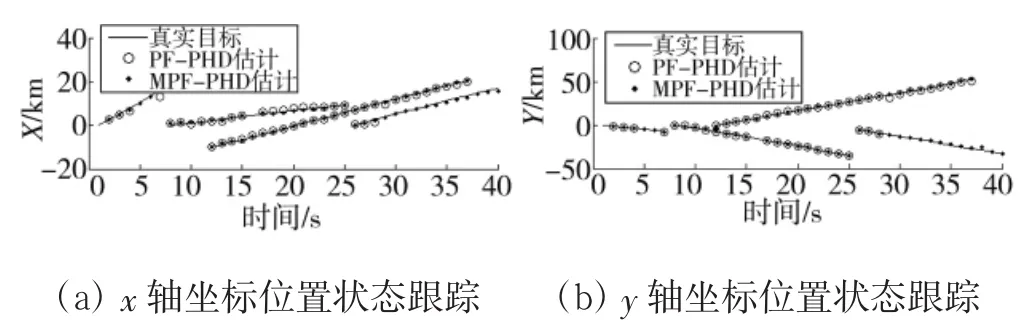
图2 场景中多目标坐标位置状态跟踪

由图2可知，PF-PHD滤波方法估计出的位置状态对比真实轨迹，跟踪效果较好，但MPF-PHD方法对于位置状态的估计总体上明显好于PF-PHD滤波方法。由图2中位置坐标状态的显示中可以看出，PF-PHD滤波方法比较容易发生目标漏检的现象，特别是在衍生出来目标的轨迹中，目标漏检现象比较多；而MPF-PHD滤波方法则表现出更加稳定且精确的跟踪。由于采用PF-PHD滤波方法而出现的多目标状态漏检的现象，容易导致系统对当前时刻目标数目的判断。从采样时刻上的漏检率看，40个采样时刻中PF-PHD方法在15个采样点上出现了漏检，而MPF-PHD方法仅在1个采样点上出现了漏检。表1为多目标采样点漏检率统计表。从表1可以看出MPF-PHD状态滤波方法在多目标采样点上的漏检率明显低于PF-PHD状态滤波方法。

表1 多目标采样点漏检率统计表

下页图3为场景中多目标数目估计的对比。由于PF-PHD状态滤波方法在多目标跟踪场景中发生的漏检现象，特别是在25 s～30 s之间场景内目标数目发生较大变化的阶段，导致图3中PF-PHD方法对于目标数目的估计存在较大误差；而本文所提出的MPF-PHD方法虽然出现了因为情况噪声而引起的目标数目估计上的少量偏差，但在目标数目发生突变的阶段仍能保持准确的数目估计。

图3 场景中多目标数目的估计

图4为场景中多目标跟踪Wasserstein距离的对比。Wasserstein距离越小，表明多目标跟踪精度越高，Wasserstein距离波动越小，表明多目标跟踪稳定性越好。如图4所示，MPF-PHD状态滤波方法对系统状态的估计无论是从精度还是稳定度上，都明显好于PF-PHD状态滤波方法。由以上3个仿真图可以看出，对于多目标的状态估计，本文所提出的MPF-PHD方法相对传统PF-PHD方法，从目标数目估计精度与状态估计精度方面都有提高。

图4 场景中多目标跟踪的Wasserstein距离

图5为PF-PHD与MPF-PHD的最优子模式分配（OSPA）距离的对比，OSPA距离是从随机有限集相似度的角度描述基于概率假设密度状态滤波方法的优劣，OSPA距离越小，表明滤波算法的估计精度越高，OSPA距离曲线随时间变化波动越小，说明滤波算法受传感器低检测概率的影响越小。由图5可以看出，MPF-PHD状态滤波方法估计精度要明显高于PF-PHD。

图5 PF-PHD平滑器与MPF-PHD的OSPA距离

表2给出了MPF-PHD状态滤波方法和PF-PHD状态滤波方法的单次更新耗时，根据表中结果可知，在同样的多目标数目的情况下，MPF-PHD算法的单次更新耗时略低于PF-PHD，算法的实时性更好，利于工程中的实际运用。

表2 各算法单次更新耗时（ms）

表3为各算法有效检测率随平均杂波数变化的比较。从表中可以看出，随着跟踪环境中杂波点迹的增长，MPF-PHD算法的有效检测率均优于PF-PHD算法。

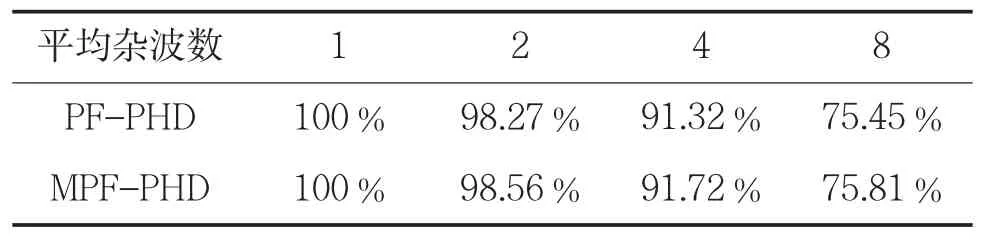
表3 各算法有效检测率随平均杂波数变化的比较

4 结论

本文提出了一种MPF-PHD方法用于对复杂情况下的多目标进行跟踪，该方法将复杂情况下的多目标状态划分为非线性状态与线性状态两部分，用PF-PHD方法估计非线性状态，用KF方法估计线性状态，同时将估计出的线性状态用来进一步优化非线性状态估计。解决了复杂情况的非线性非高斯性给多目标跟踪所带来的目标漏检的问题，同时进一步提高了跟踪精度。实验结果表明，在目标数目估计的精度、目标状态估计精度和实时性方面，MPF-PHD方法都要优于传统的PF-PHD方法。

［1］PURANIK S，TUGNAIT J K.Tracking of multiple maneuvering targets using multiscan JPDA and IMM filtering［J］. IEEE Transactions on Aerospace&Electronic Systems Aes，2007，43（1）：23-35.

［2］BLACKMAN S S.Multiple hypothesis tracking for multiple target tracking［J］.IEEE Aerospace&Electronic Systems Magazine，2004，19（1）：5-18.

［3］MAHLER R P S.Multitarget Bayes filtering via first order multitarget moments［J］.IEEE Transactions on Aerospace and Electronic Systems，2003，39（4）：1152-1178.

［4］VO B N，MA W K.The gaussian mixture probability hypothesis density filer［J］.IEEE Transactions on Signal Processing，2006，54（11）：4091-4104.

［5］ANDERSON K D.Radar detection of low-altitude targets in a maritime environment［J］.IEEE Transactions on Antennas and Propagation，1995，43（6）：609-613.

［6］BREKKE E，HALLINGSTAD O，GLATTETRE J.Tracking small targets in heavy-tailed clutter using amplitude information［J］.IEEE Journal of Oceanic Engineering，2010，35（2）：314-329.

［7］MOYER L R，SPAK J，LAMANNA P.A multi-dimensional hough transform-based track-before-detect technique for detecting weak targets in strong clutter backgrounds［J］. IEEE Transaction on Aerospace and Electronic Systems，2011，47（4）：3062-3068.

［8］SCHOH T，GUSTAFSSON F，NORDLUND P J.Marginalized particle filters for mixed linear/nonlinear state space models［J］.IEEE Trans on Signal Processing，2005，53（7）：2279-2289.

［9］连峰，韩崇昭，刘伟峰，等.多模型概率假设密度平滑器［J］.自动化学报，2010，36（2）：939-948.

［10］庄泽森，张建秋，尹建君.Rao-Blackwellized粒子概率假设密度滤波算法［J］.航空学报，2009，30（4）：698-705.

［11］CATTIVELLI F S，SAYED A H.Diffusion strategies for distributed kalman filtering and smoothing［J］.IEEE Transactionson AutomaticControl，2010，55（9）：2069-2084.

［12］PETETINY，MORELANDEM，DESBOUVRIESF. marginalized particle PHD filters for multiple object bayesian filtering［J］.IEEE Transactions on Aerospace and Electronic Systems，2014，50（2）：1182-1196.

［13］SAHA S，GUSTAFSSON F.Marginalized particle filter for dependent gaussian noise processes［C］//2012 IEEE Aerospace Conference，2012：1-6.

［14］陈金广，马全海.Parfor模式在粒子概率假设密度滤波中的应用［J］.四川兵工学报，2015，36（12）：75-79.

Multi-target Tracking Based on Marginal Particle Filtering-Probability Hypothesis Density

YU Yang，SONG Jian-hui，LIU Yan-ju，SI Guan-nan
（School of Automation and Electrical Engineering，Shenyang Ligong University，Shenyang 110159，China）

In view of the multi-target tracking problem under complex conditions，this paper puts forward a kind of marginalized particle filtering-probability hypothesis density（MPF-PHD）method. Firstly the nonlinear and linear state in the state vector of multi-target under the complex conditions is extracted separately in this method.Then using particle probability hypothesis density filter（PF-PHD）nonlinear state estimation，Kalman Filter（KF）is used to estimate the linear state，and the linear state estimation of nonlinear state related is adopted to optimize the nonlinear state estimation.According to contrast MPF-PHD method with the traditional PF-PHD method simulation，it is verified that the MPFPHD method can effectively solve the multi-target tracking under complex conditions of residual problem，the multiple target state estimation accuracy is improved.

marginal particle filtering-probability hypothesis density（MPF-PHD），multi-target tracking，nonlinear state estimation，kalman filtering

TN953

A

1002-0640（2017）05-0014-05

2016-03-09

2016-05-07

国家自然科学基金（61373089）；辽宁省教育厅基金资助项目（LT2012005）

于 洋（1963- ），男，吉林白山人，硕士，教授。研究方向：智能检测与网络化测控。