关于不定积分的表达式

韩清

（广东外语外贸大学南国商学院公共课教学部，广东广州510545）

关于不定积分的表达式

韩清

（广东外语外贸大学南国商学院公共课教学部，广东广州510545）

讨论了不定积分一般表达式的不足，改进了不定积分相等的内涵。

不定积分；一般表达式；积分常数

在微积分里，众所周知，一个给定函数的原函数不止一个。我们有下面熟知的结果［1］：

设F（x）是函数f（x）的一个原函数，则f（x）的所有原函数都具有F（x）+C的形式。这里，C为任意常数，也就是所谓的积分常数（the constant of integration）。

教科书上都把f（x）的不定积分定义为上述原函数的“一般表达式”［2］，即

这个所谓的一般表达式意思有些含糊,在教学时学生也不太容易理解,会产生下面一些问题：

（Ⅰ）为了凑常数，往往要有“前瞻性”，以凑最终结果。如此表达既繁琐，又不自然。

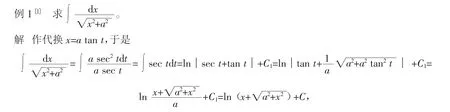
其中，记C=C1-ln a，仍为任意常数。

例1中，为凑出最终的C，提前几行就要“预见性”地在积分常数加下标，写成C1。

（Ⅱ）容易产生1=0性质的概念错误。

例2，基本积分公式［2］

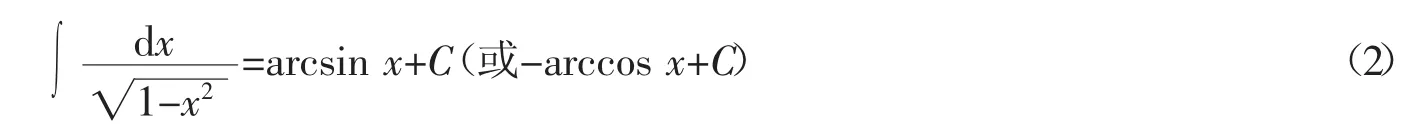
容易让人认为

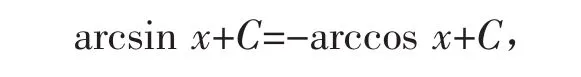
从而产生

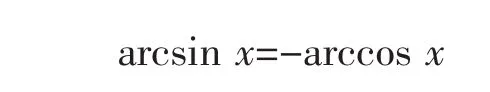
实际上，如果变换思维，把不定积分严格地定义为“所有原函数的集合”，即

那么，就不会产生前述的一些问题和误解。

也就是说，这里，把原函数与不定积分两个概念清楚区分开：前者是一个具体函数，后者则是函数族，是个集合。

不过，如果全部按上面的集合写法来表达积分又很繁琐（这大概也是教科书不这么表述的根本原因）。故此，可以把式（3）简写成紧凑的形式，即

式（4）写起来与式（1）一样，但内涵不同。确切地说，在式（3）定义下的不定积分计算中的等式，其实不是一般四则运算意义下的相等，而是集合运算的相等。

此处，英文所用的术语是“up to”，也就是“常数忽略不计”意义下的相等。如此，既不会有概念上的疑惑，也不会增加书写麻烦。

例如，上述例1中的表达式写成

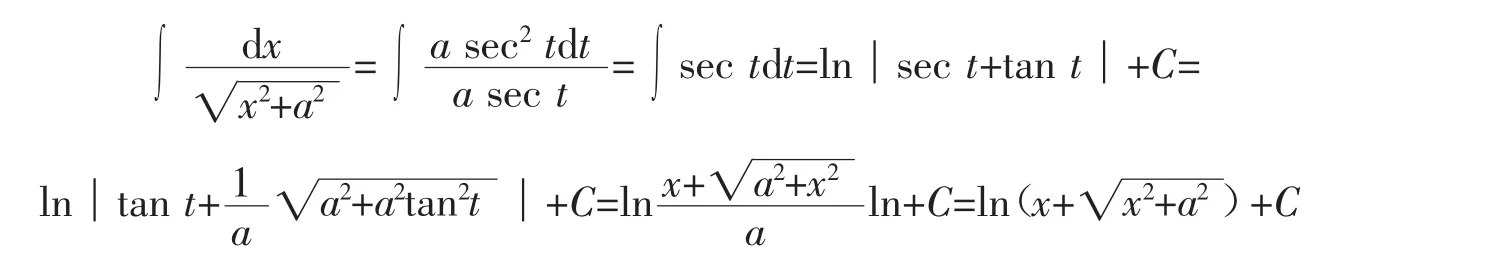
即可，而不必引进C=C1-lna这样啰嗦的写法。

关键之处是：“但凡是常数，都可以忽略不计”。

有了上面对不定积分理解的改变，可以很容易地跟学生解释：在积分计算过程中，只要还有其他积分号算出的积分就不必加常数；而一旦没有了积分号，就一定要加任意常数符号C，例如

［1］陈传璋.数学分析:上册［M］.2版.北京:高等教育出版社,1983:235,245.

［2］隋如彬.微积分［M］.2版.北京:科学出版社,2012:181,185.

【责任编辑：王桂珍 foshanwgzh@163.com】

A note about the expressing of the indefinite integral

HAN Qing
（Faculty of Common Courses,South China Business College of Guangdong Universityof Foreign Studies, Guangzhou 510545,China）

In this paper,some deficiencies of the expressing of the indefinite integral have been discussed,and the connotation ofthe equation ofthe indefinite integral has been improved.

indefinite integral;general expression;the constant ofintegration

O172.2

A

1008-0171（2017）03-0028-02

2017-02-22

国家自然科学基金资助项目（11671153）

韩 清（1964-），男，江西九江人，广东外语外贸大学南国商学院副教授，博士。