一类非线性Schrödinger方程驻波解的存在性

陈风仪，姚仰新

（华南理工大学数学学院，广东广州510640）

一类非线性Schrödinger方程驻波解的存在性

陈风仪，姚仰新*

（华南理工大学数学学院，广东广州510640）

证明了等离子体中出现的一类非线性Schrödinger方程驻波解的存在性。

非线性；Schrödinger方程；驻波解

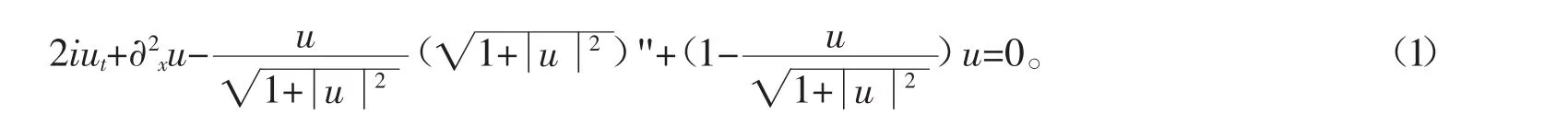
如在文献［1］中，作者研究了形如下面非线性等离子体波方程

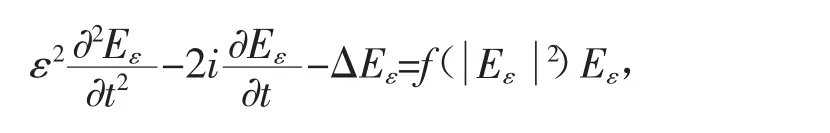
对f进行具体地假设，证明了当ε→0时，Eε可收敛到相应Schrödinger方程中的E，即有

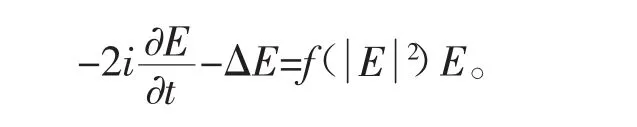
同样，文献［2］讨论了和上述方程类似的结果，即

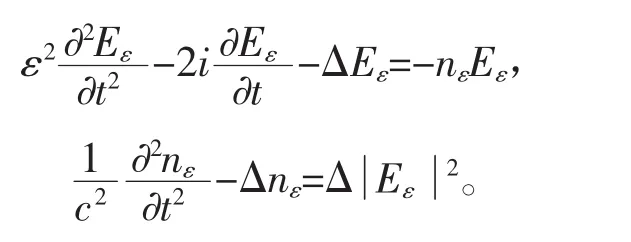
在文献［3］中，令下面等离子体波方程的ε→0（低密度等离子情形下），即作者得出了uε可收敛于相应的非线性方程中的u的结果。类似方程的研究可以参考文献［4-6］。

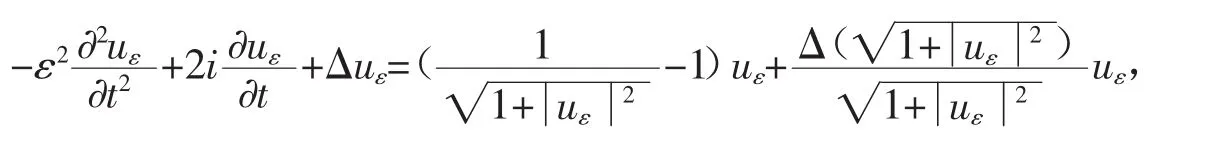
而本文主要关注方程（1）的形如下面形式的解的存在性

将方程（2）代入方程（1），有

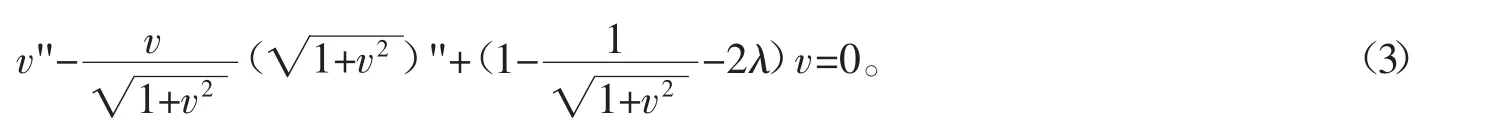
我们可给出以下定理：

定理［7］方程（1）存在形如方程（2）形式的驻波解，即

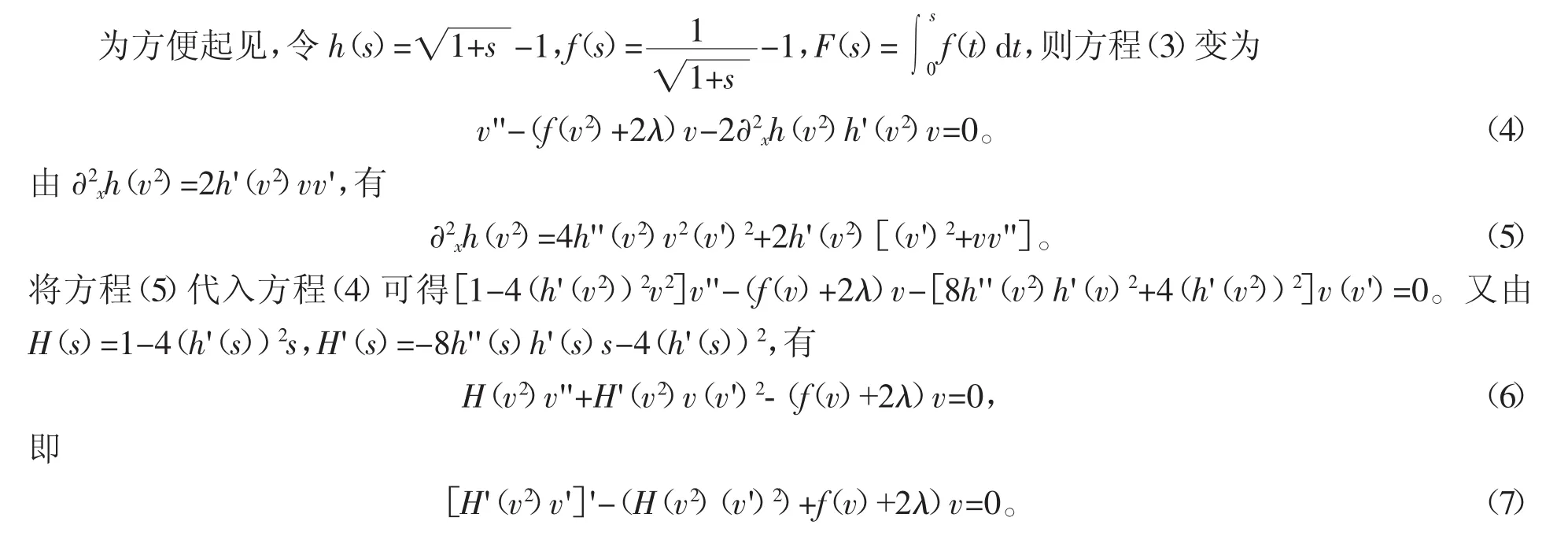
若H（v2）≠0，方程（7）也可以写为

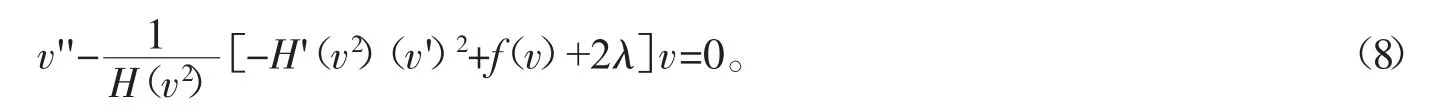
则要讨论方程（1）广义解的存在性，即要讨论方程（7）（或（8））解的存在性。下面给出一个引理。

引理［7］方程中任意解v（x）都满足

证明 对上面等式的左边求导，可得

故等式成立。

定理的证明 首先注意到，可以找到一个满足

的最小x0（＞0），使得对任何及对某一成立。

对上式两边平方可得

现在，考虑方程（7）的初值问题，令v（0）=x0，v'（0）=0，易见H2（v（0））=H（x02）＞0，x∈M。实际上，在M内，0＜v（x）＜x0。

设存在x1∈M，v（x1）=0，且对x∈［0，x1），则由引理有

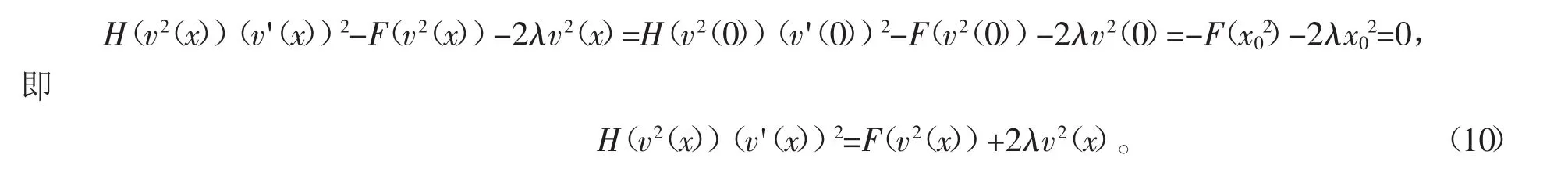
令x=x2，有v'（x2）=0。根据解的唯一性，若v（x）≡0，x∈M，则因与v（0）=x0矛盾，故v（x）＞0，x∈M。

下面逐条验证v（x）的相关性质，即v（-x）=v（x），对任何x＞0，v'（x）＜0与lim v（x）=0。

首先，显然v（-x）也是方程（7）在初值条件下的解，由解的唯一性知v（-x）=v（x）。

现假设存在某一x4＞0，且v'（x4）=0，则由方程（10）有F（v2（x4））+2λv2（x4）=0，v（x4）＜x0，故对x＞0，v'（x）＜0。

下面证明方程（7）的解平移后仍是该方程的解，即该解唯一。设w（x）是方程（7）的另一个解，将其在达到最大值的点平移到原点，则有w'（0）=0，设w（0）=w0，有w（x）=w（-x）且

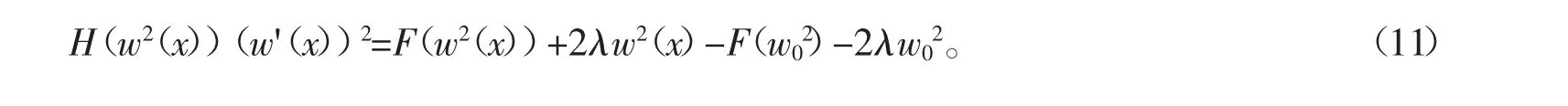
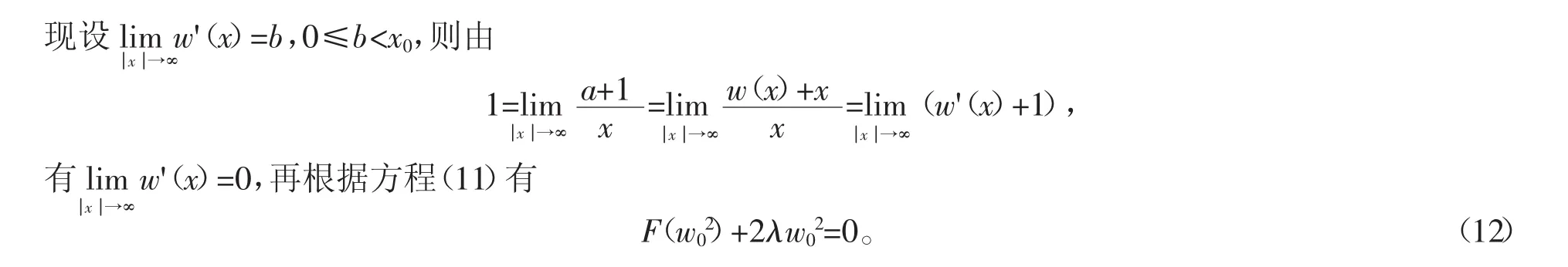
假设w（0）=w0＞x0，则存在x5＞0使得w（x5）=x0且当x∈（0，x5）时，w（x）＞x0。由方程（11）和方程（12），取x=x5有

因而w'（x5）=0。同时由方程（8）有故w（x）在x3上达到最大值，但由假设可知存在区间（0，x5），使得对其中的x有w（x）＞x0，因而矛盾，假设不成立，即有0＜w（0）≤x0，又由方程（12）知w0=x0，由解的唯一性知w（x）=v（x）。

［1］BERGÉL,COLIN T.A singular perturbation problem for an envelope equation in plasma physics［J］.Phys D,1995,84: 437-459.

［2］BERGÉL,BIDÉGARAY B,COLIN T.A perturbative analysis of the time-envelope approximation in strong Langmuir turbulence［J］.Phys D,1996,95:351-379.

［3］COLIN M.Approximation of a quasilinear Schr ödinger equation by a Kelin-Gordon equation in space dimension 2［J］. Asymptotic Anal,2003,34:275-309.

［4］BOUARD A,HAYASHI N,SAUT J.Global existence of small solutions to a relativistic nonlinear Schrödinger equation［J］. Commun Math Phy,1997,189（1）:73-105.

［5］AGRAWALGP,贾东方,余震虹,等.非线性光纤光学原理及应用［M］.北京:电子工业出版社,2003.

［6］SHENYT,WANGYJ.Soliton solutions for generalized quasilinear Schrödinger equations［J］.Nonlinear Analysis TMA,2013, 80:194-201.

［7］BRÜLL,LANGE H,KÖLN.Stationary,oscillatory and solitary wave type solution of singular nonlinear Schrödinger equations［J］.Math Meth in the Appl Sci,1986,8:559-575.

【责任编辑：王桂珍 foshanwgzh@163.com】

The existence of stationary solutions for a class of nonlinear Schrödinger equation

CHEN Feng-yi,YAO Yang-xin
（School of Mathematics,South China University of Technology,Guangzhou 510640,China）

This article established the existence of stationary solution for a class of nonlinear Schrödinger equation derived fromplasma.

nonlinear;Schrödinger equation;stationary solution

O175.25

A

1008-0171（2017）03-0019-04

2016-09-23

国家自然科学基金资助项目（11201154）

陈风仪（1992-），女，江西赣州人，华南理工大学硕士研究生。

*通信作者：姚仰新（1957-），男，广东广州人，华南理工大学教授，博士。