基于遗传算法优化的约束背景双线性分解算法用于改进高效液相色谱灰色分析体系的校正结果

张雅雄, 聂先玲

(磁性分子与磁性信息材料教育部重点实验室, 山西师范大学化学与材料科学学院, 山西 临汾 041004)

研究论文

基于遗传算法优化的约束背景双线性分解算法用于改进高效液相色谱灰色分析体系的校正结果

张雅雄*, 聂先玲

(磁性分子与磁性信息材料教育部重点实验室, 山西师范大学化学与材料科学学院, 山西 临汾 041004)

该文采用约束背景双线性分解算法(CBBL)对以高效液相色谱(HPLC)方法分离分析的灰色分析体系进行了多元校正研究。针对采用包括CBBL在内的矩阵校正方法处理HPLC灰色分析体系的固有缺陷,即在相关组分的色谱保留时间重现性较低的情形下多元校正的结果不理想,对CBBL方法进行了改进,即将待测组分的浓度与组分的色谱保留时间同时作为优化的参量引入CBBL,并采用遗传算法(GA)优化CBBL,对于模拟的组分保留时间飘移严重的HPLC灰色分析体系及保留时间重现性不佳的多种酚类化合物组成的实际HPLC灰色分析体系进行了多元校正分析,成功克服了经典CBBL的固有缺陷,取得了较理想的多元校正结果。另外,该研究所建议的方法的校正结果也显著优于传统的残差双线性分解法(RBL)以及秩消失因子分析法(RAFA)。

约束背景双线性分解算法;遗传算法;高效液相色谱灰色分析体系;改进多元校正方法

随着现代分析化学分析手段的仪器化和分析对象的复杂化,得到的仪器分析信号日益复杂,且其中包含的有用信息也日益丰富,对此类仪器分析信号进行解析以提取出最大量的有用信息就成为化学计量学研究的重要目标[1]。根据分析信号的数据类型,通常可分作标量类型数据、矢量类型数据、矩阵类型数据以及张量类型数据。显然,维数越高的数据类型其所蕴含的信息量越丰富,进而可以用于解析的分析化学体系的复杂性也越高。依据分析体系复杂性及分析要求的不同,文献[1]将复杂的多组分分析体系形象地划分为白、灰以及黑3类。其中,灰色分析体系的基本特征为:已知待测物存在于待分析的样本中,但是否存在别的未知干扰是不明确的,分析的目的是在未知干扰存在的情况下,直接对待测物进行定量分析。此类分析体系是分析化学工作者遇到的频率最高的一类体系。

对于灰色分析体系的多元校正方法,一般分为矢量校正方法和矩阵校正方法。由于在没有较强的先决条件的情况下,矢量校正方法只能给出可能解,因此具有一定的局限性。矩阵校正方法中比较著名的有秩消失因子分析法(RAFA)[2]、残差双线性分解法(RBL)[3]和约束背景双线性分解法[4,5]。在通常状况下,这些方法都可以对待测组分进行快速准确的定量,给出具有物理意义的唯一解。但文献[1]指出上述矩阵校正方法存在两大缺陷:1.若无法做到对于某一矩阵的秩的正确估计,则上述矩阵校正方法可能无法得到准确的唯一解;2.对于色谱过程所产生的数据,若组分保留时间的重现性较差,则也可能给上述方法的运用带来困难。

作为一种常用的仪器分析方法,色谱方法在现代分析化学中占有重要地位。但在实际色谱样品中常含有结构、性质相似的组分,如同系物、同分异构体、化合物及其衍生物等,这些物质在流动相和固定相中的保留行为差异不大,往往导致色谱峰的重叠。另外,在复杂多组分体系中,常含有未知杂质的干扰,而现代分析化学的主要任务之一就是对复杂多组分体系进行定性定量分析。但要实现理想的色谱分离过程,即使在采用计算机方法模拟及优化色谱分离过程的情况下[6],通常仍是一项费时费力的工作。因此,发展针对色谱灰色分析体系的多元校正方法尤为重要。另一方面,色谱条件难于控制,可能使组分保留时间的重现性较差[7]。文献[5]虽采用遗传算法(GA)优化的约束背景双线性分解算法(CBBL)研究了HPLC灰色分析体系的多元校正问题,但并未涉及组分保留时间重现性不佳时该方法的适用性问题。另外,近年来关于多元校正与分辨方法的文献报道[8-13]中也未见对此问题的探讨。

综上所述,本文拟对CBBL方法予以发展,使其能够适用于组分保留时间重现性不佳的HPLC灰色分析体系的多元校正问题。

1 理论

1.1 约束背景双线性分解算法

该算法的详细过程见文献[4],在此仅给出其概略。所谓二维数据的“双线性”[4]是指纯组分所得数据矩阵的秩为1,即该数据矩阵X可表示为两个矢量(在本文中,所有矢量如无特别说明均为列矢量)的乘积形式。

X=tpt

(1)

式(1)中,t表示液相色谱的色谱流出曲线,pt表示HPLC-二极管阵列检测器(DAD)所记录的该组分的标准光谱。

灰色分析体系的数学模型可表示为:

(i=1, 2,...,n;j=1, 2,...,m)

(2)

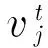
虽然通常情形下很难准确估计量测误差的统计特征,但通常假定量测误差服从零均值等方差的正态分布仍可认为是合理的。为了对量测误差的方差给出合理的估计,本文通过小波变换方法对HPLC-DAD数据进行滤噪处理,使其随机误差的方差趋近于零。因此,本文的优化过程采用了下述目标函数:

(3)

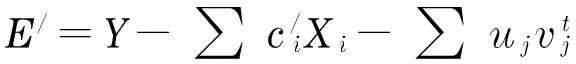
为了提高优化效率,CBBL方法引入了约束条件,对待测组分的浓度搜索范围进行限制。其约束条件为[5]:

(4)

1.2 基于数值遗传算法的优化策略

本文采用数值遗传算法[6]优化CBBL方法。组成遗传算法中的“染色体”的“基因”包括各个组分的初始浓度ci以及各组分的初始保留时间ti。引入组分保留时间作为优化参量的目的在于使CBBL方法对于保留时间重现性差的HPLC灰色分析体系也有理想的校正效果。因此,对于发生保留时间飘移的色谱体系,引入各组分保留时间ti的实质是使得式(2)中的Y、Xi、R以及E各项均成为保留时间ti的函数。其含义指:对于一个待测的HPLC二维数据灰色分析体系,如果相关组分(包括待测组分与干扰组分)的保留时间发生飘移(相对于标准物体系),那么相对于以标准物组分所采集的上述响应矩阵,待测体系的上述响应矩阵无疑都至少在保留时间轴上的数据会发生平移,还由于误差矩阵E的随机特征,故总响应矩阵Y也必然发生变化。即不仅各组分的浓度,而且各组分的保留时间ti也成为影响Y的因素。选择遗传算法的适当参数,可以实现CBBL在上述条件下的全局优化。

另外,为了克服文献[1]所指出的上述矩阵校正方法的第一大缺陷,本研究工作中采用了特征值比的方法[14]准确确定了相关矩阵的秩。

2 实验部分

2.1 数据模拟方法

本文利用指数修正的高斯色谱峰模型(EMG)[6]模拟了HPLC单峰,通过EMG模型模拟的色谱峰能够与实际色谱峰的拖尾和不对称性很好地匹配。式(5)为指数修正的高斯方程:

(5)

其中,Z=[(t-tg)/σg]-(σg/τ),代表积分上限,A为色谱峰的峰面积,tg(g代表高斯色谱峰模型)为色谱峰的保留时间,σg为色谱峰高斯分布的标准偏差,主要影响峰的拖尾程度,σg参数值越大,色谱峰的拖尾越严重。τ是呈指数衰减的时间常数,τ/σg主要衡量峰的不对称性,比值越接近1,峰的对称性就越好。V表示模拟色谱曲线信号强度,t表示色谱曲线横坐标(即保留时间),x表示高斯函数中的指数项。

在HPLC-DAD系统所产生的二维数据的另一个维度上应是组分的光谱信息,其模拟表达式如下:

S(λ)=[psin(vλ)sin(fλ)+c]/s

(6)

式(6)中,λ代表波长,S代表模拟光谱信号强度,其余参数均为非负经验常数,通过调节各个常数的大小,可以改变函数S(λ)的取值,从而实现不同组分的光谱的模拟。结合式(1)、(5)以及(6),可模拟出符合“双线性”特征的二维数据。

2.2 实验条件

2.2.1 仪器

Waters e2695型HPLC仪、Waters 2998二极管阵列检测器、Empower色谱工作站(Waters科技(上海)有限公司,美国)。

2.2.2 试剂及样品的制备

体系1:对苯二酚(上海迈坤化工有限公司)、间苯二酚(天津化学试剂公司)、苯酚(天津Kermel化学试剂研发中心)、4-硝基苯酚(上海国药集团化学试剂有限公司)和甲醇(洛阳市化学试剂厂)均为分析纯。用甲醇-蒸馏水体积比为58∶42的色谱级溶液分别配制3种不同浓度的对苯二酚、间苯二酚、苯酚、4-硝基苯酚的纯组分溶液及混合溶液,其中一种作为标准溶液样品A,另外两种不同浓度的溶液为样品B和样品C。对苯二酚、苯酚、4-硝基苯酚3种组分为待测组分,间苯二酚为干扰背景组分。

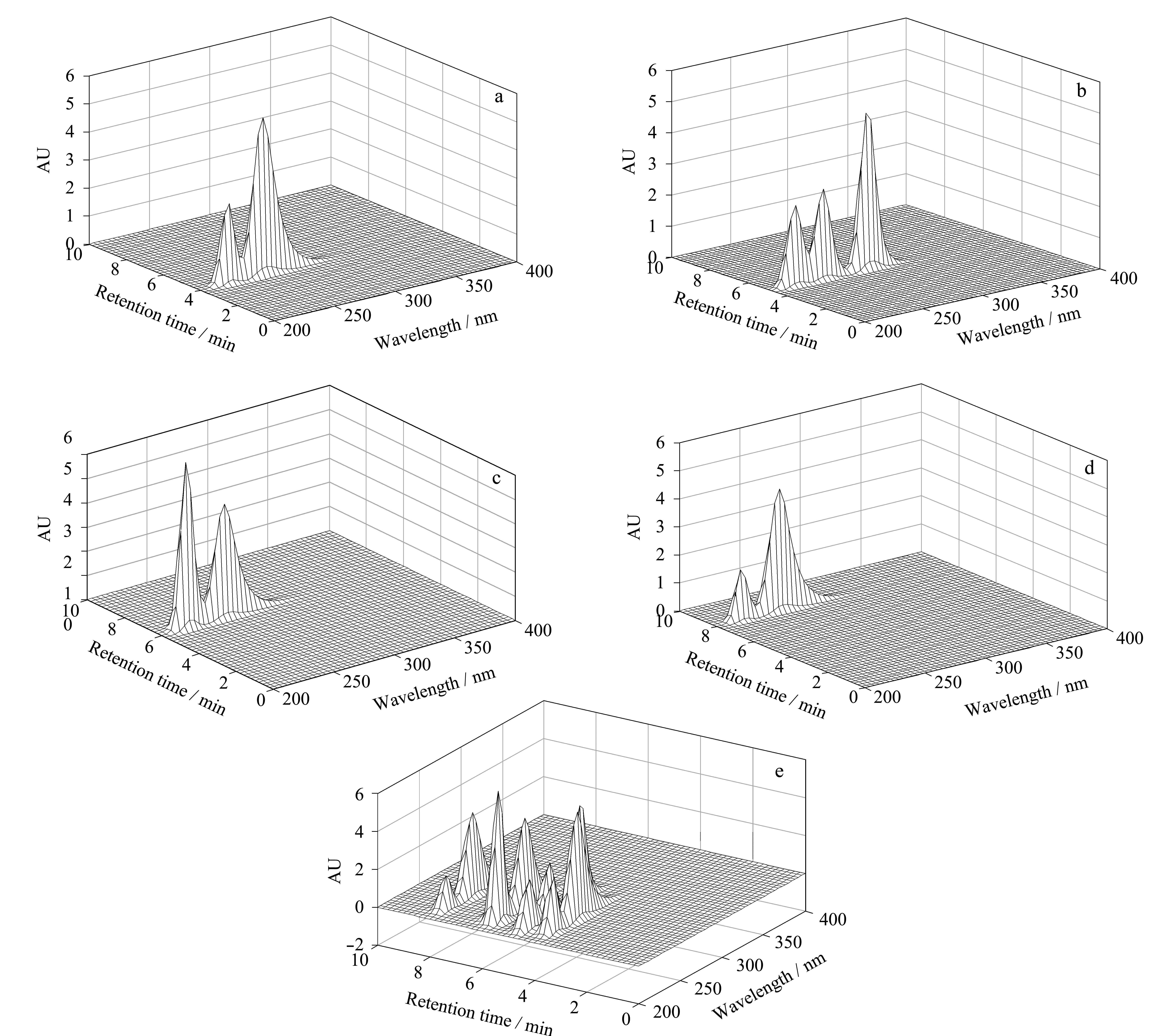
图 1 模拟纯组分和混合物的标准三维色谱图Fig. 1 Simulated standard 3D-chromatograms of the pure components and their mixture a-d indicate the simulated four pure components; e. mixture of a-d.

体系2:对苯二酚、间苯二酚、邻苯二酚、苯酚、3-硝基苯酚(上海国药集团化学试剂有限公司)、4-硝基苯酚、甲醇均为分析纯。配制甲醇-水体积比为61∶39的色谱级溶液,用此溶液分别配制3种不同浓度的对苯二酚、间苯二酚、邻苯二酚、苯酚、4-硝基苯酚、3-硝基苯酚的纯组分溶液及混合溶液,其中一种作为标准溶液样品A,另外两种不同浓度的溶液为样品B和样品C。其中,对苯二酚、邻苯二酚、苯酚、3-硝基苯酚、4-硝基苯酚5种组分为待测组分,间苯二酚为干扰背景组分。

2.2.3 色谱条件

体系1的色谱柱为Gemini C18(250 mm×4.6 mm, 10 μm)柱。流动相:甲醇-水(体积比为58∶42)。流速:1.0 mL/min。柱温:35 ℃。检测波长:200～400 nm。进样量:50 μL。进样次数:每个样品进样3次。

体系2的色谱柱为Gemini C18(250 mm×4.6 mm, 10 μm)柱。流动相:甲醇-水(体积比为61∶39)。流速:1.2 mL/min。柱温:35 ℃。检测波长:200～400 nm。进样量:50 μL。进样次数:每个样品进样3次。

3 结果与讨论

3.1 模拟HPLC灰色分析体系的校正

为了验证方法的有效性,首先考察方法对模拟体系的适用性。为此,本文模拟了四组分色谱体系。模拟所得单组分以及四组分三维标准谱图见图1。混合物的总响应矩阵通过各组分模拟响应矩阵相加构成。为更逼真地模拟实际色谱体系,在待测模拟谱图中加入了服从正态分布的零均值等方差的随机误差。对应于标准谱图的混合物样品标识为A。为模拟出浓度及保留时间均发生变化的待测混合物体系,将每种模拟组分的浓度与所对应模拟峰的面积设定为特定比例,同时使各组分的保留时间产生随机偏移,保留时间的约束范围为(ti±0.5) min,依据以上原则,模拟出待测混合样本体系B与C。

在混合体系的a、b、c、d 4种纯组分中,b为背景干扰组分,a、c、d为待测组分。在进行CBBL方法的GA优化校正之前,首先采用小波变换方法抑制B与C混合体系三维色谱数据中的随机误差。表1与表2为优化校正的结果。结果表明,即使在模拟组分的浓度与保留时间均发生较大变化的情形下,所建议的校正方法仍可得到较理想的结果。待测组分与干扰组分的浓度与保留时间均得到了较为准确地估计(相对误差绝对值小于3%)。

为了与本文所建议的方法进行比较,经典CBBL方法的校正结果也于表3中给出。由于各响应矩阵的保留时间的高度重现性,经典的CBBL方法对于标准混合溶液的校正结果几乎是理想的。而对于待测混合体系,由于响应矩阵的保留时间发生了飘移,校正结果的准确度与表1相比显著变差。这一结果验证了文献[1]对于经典矩阵校正方法局限性的结论。另外,经典CBBL方法不涉及组分保留时间的校正,也不要求计算干扰组分(甚至干扰组分的定性信息可能也是未知的)的浓度。

表 1 模拟体系的组分浓度(10-4mol/L)优化校正结果

c: concentration; T-c: target concentration; Ca-c: calculated concentration; a-d indicate the simulated components; A, B, and C indicate the simulated standard and the two test solutions, respectively.

表 2 模拟体系的组分保留时间(min)优化校正结果

tR: retention time; T-tR: target retention time; Ca-tR: calculated retention time; A, B, and C indicate the simulated standard and the two test solutions, respectively.

表 3 模拟体系的组分浓度(10-4mol/L)基于经典约束背景双线性分解算法的优化校正结果

A, B, and C indicate the simulated standard and the two test solutions, respectively. -: not detected.

3.2 HPLC灰色分析体系的校正

在对模拟数据取得成功的基础上,本文拟将所建议的方法推广到实验体系,分别以四组分体系(体系1)与六组分体系(体系2)作为考察对象。

3.2.1 对体系1的研究

对于该体系,同样采集视为标准的各个纯组分以及混合体系的三维色谱图,该系列记为A,所得谱图见图2。同样配制待分析混合体系B与C, B、C与A含有相同的组成,但各个组分的浓度不同,保留时间也发生了随机飘移。经过对待测混合体系B与C的三维谱图采用小波变换滤除随机误差之后,GA优化的CBBL方法校正后的混合体系B与C的各组分浓度及保留时间分别见表4和表5。结果表明,在实验体系1中,即使在相关组分的浓度与保留时间均发生较大变化的情形下,所建议的校正方法仍可得到较理想的结果。在体系1中,待测组分与干扰组分的浓度与保留时间均得到了较为准确地估计(相对误差绝对值小于5%)。

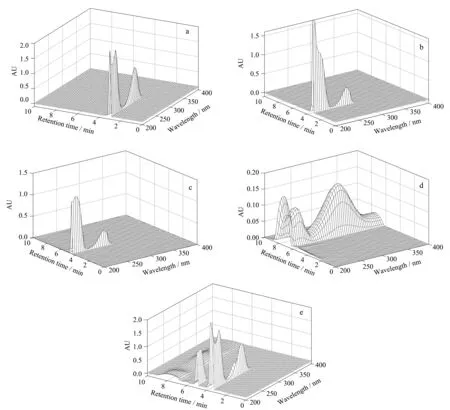
图 2 体系1纯组分和混合物的标准三维色谱图Fig. 2 Standard 3D-chromatograms of the pure components and their mixture in system 1a. hydroquinone; b. resorcinol; c. phenol; d. 4-nitrophenol; e. the mixture of a-d.

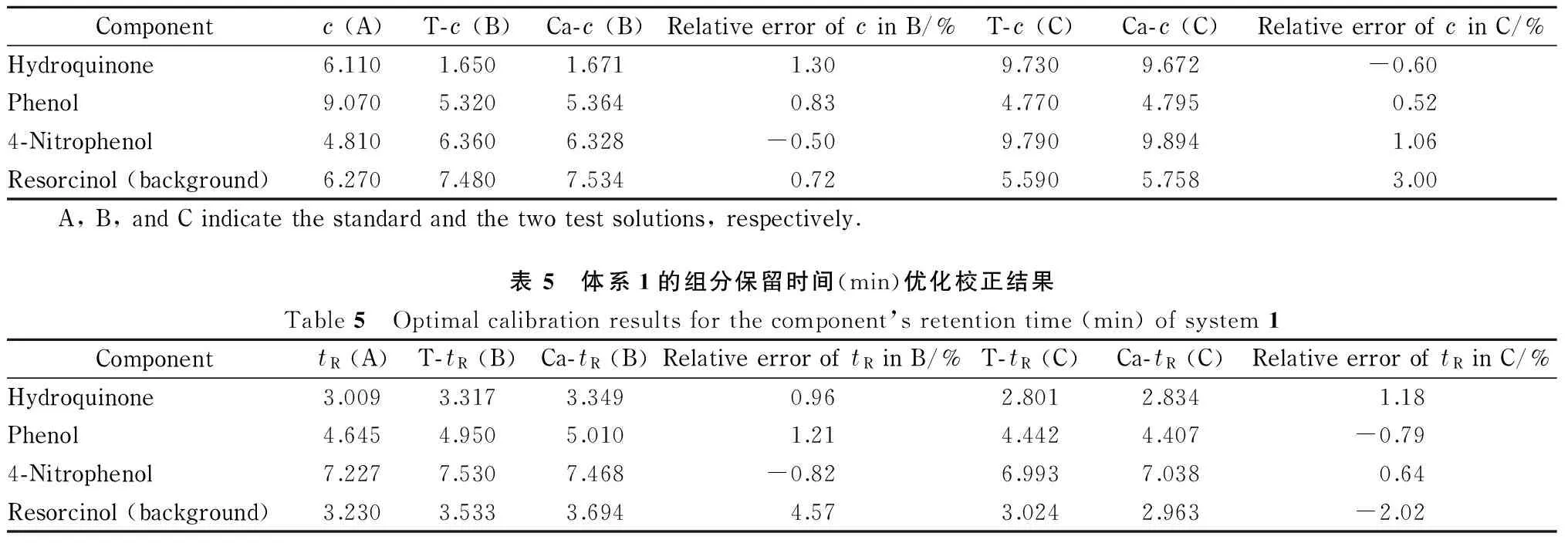
Componentc(A)T-c(B)Ca-c(B)RelativeerrorofcinB/%T-c(C)Ca-c(C)RelativeerrorofcinC/%Hydroquinone6.1101.6501.6711.309.7309.672-0.60Phenol9.0705.3205.3640.834.7704.7950.524-Nitrophenol4.8106.3606.328-0.509.7909.8941.06Resorcinol(background)6.2707.4807.5340.725.5905.7583.00 A,B,andCindicatethestandardandthetwotestsolutions,respectively.表5 体系1的组分保留时间(min)优化校正结果Table5 Optimalcalibrationresultsforthecomponent’sretentiontime(min)ofsystem1ComponenttR(A)T-tR(B)Ca-tR(B)RelativeerroroftRinB/%T-tR(C)Ca-tR(C)RelativeerroroftRinC/%Hydroquinone3.0093.3173.3490.962.8012.8341.18Phenol4.6454.9505.0101.214.4424.407-0.794-Nitrophenol7.2277.5307.468-0.826.9937.0380.64Resorcinol(background)3.2303.5333.6944.573.0242.963-2.02

A, B, and C indicate the standard and the two test solutions, respectively.

对于体系1,为了与本文所建议的方法进行比较,经典CBBL方法的校正结果也于表6中给出。对比表4与表6可知,经典CBBL方法对于保留时间发生较大飘移的实验体系,其校正结果显著变差。

另外,本文也考察了RAFA和RBL两种经典矩阵校正方法对于体系1的校正结果(见表7和表8)。结果表明,经典的RAFA与RBL方法也只能对保留时间重现性较好的体系(A溶液)给出准确度较高的校正结果。与此类经典方法相比,本文所建议的方法也具有优势。

表 6 体系1的组分浓度(10-4mol/L)基于经典CBBL方法的优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

表 7 体系1的组分浓度(10-4mol/L)基于经典秩消失因子分析法的优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

表 8 体系1的组分浓度(10-4mol/L)基于经典残差双线性分解法方法的优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

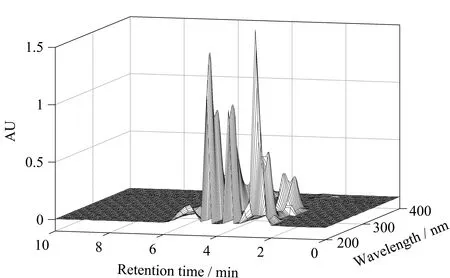
图 3 体系2混合物的标准三维色谱图Fig. 3 Standard 3D-chromatogram of the mixture in system 2

3.2.2 对体系2的研究

本部分对体系2也采用上述优化策略进行了多元校正研究。图3为体系2的混合体系的标准三维色谱图(标记为样品A)。待测试样品分别标记为B与C。其多元校正的结果见表9和表10。结果表明,在实验体系2中,即使在相关组分的浓度与保留时间均发生较大变化的情形下,所建议的校正方法也可得到较理想的结果。在体系2中,待测组分与干扰组分的浓度与保留时间均得到了较为准确地估计(相对误差绝对值小于10%)。

表11为体系2经典CBBL方法的校正结果。对于体系2,对比表9与表11的结果表明,经典CBBL方法对于保留时间发生较大飘移的实验体系,

其校正结果显著变差。

RAFA和RBL校正方法的校正结果分别在表12和表13中给出。结果同样表明经典的RAFA与RBL方法只能对保留时间重现性较好的体系(A溶液)给出准确度较高的校正结果。与此类经典方法相比,本文所建议的方法对于体系2的多元校正也具有优势。

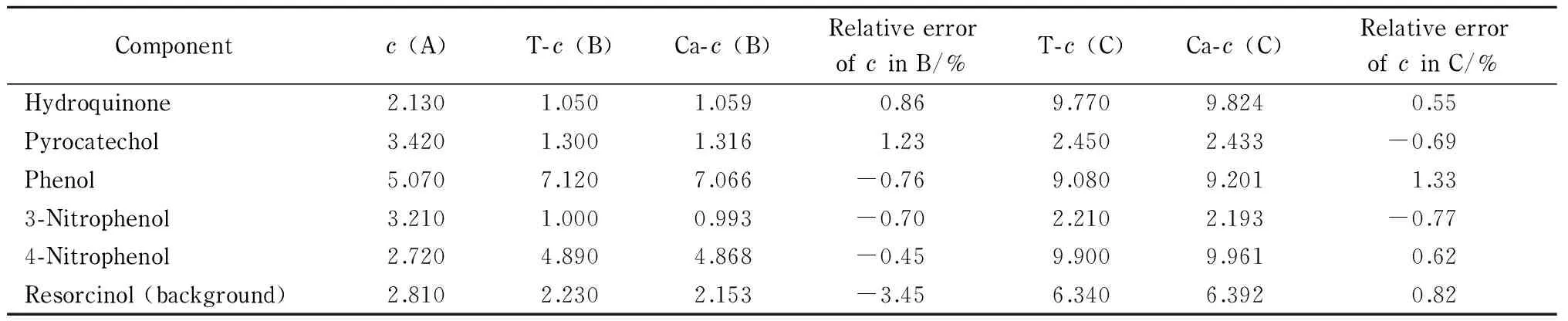
表 9 体系2的组分浓度(10-4mol/L)优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

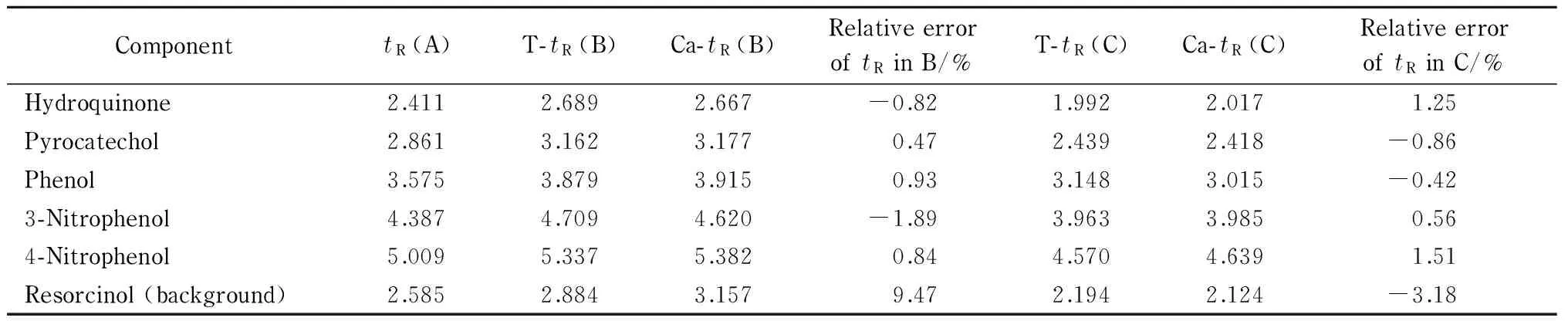
表 10 体系2的组分保留时间(min)优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

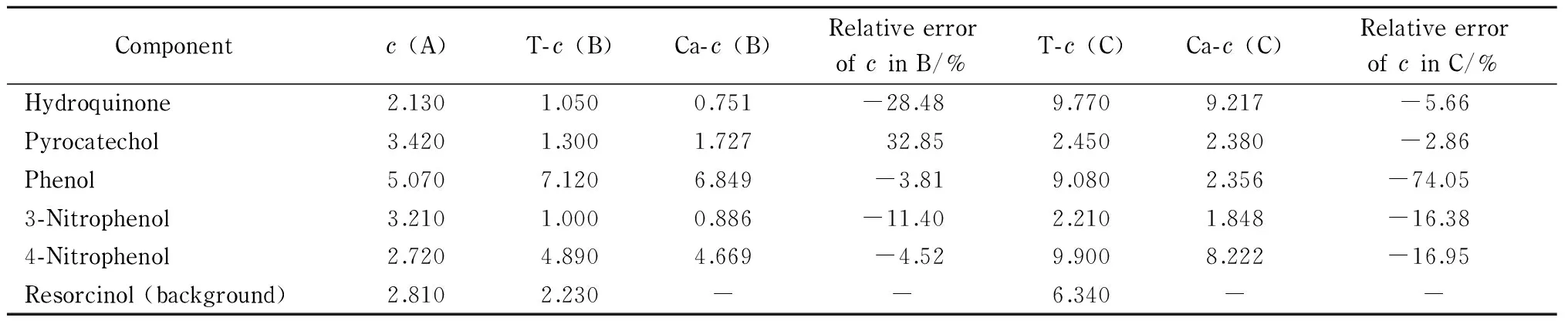
表 11 体系2的组分浓度(10-4mol/L)基于经典CBBL方法的优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

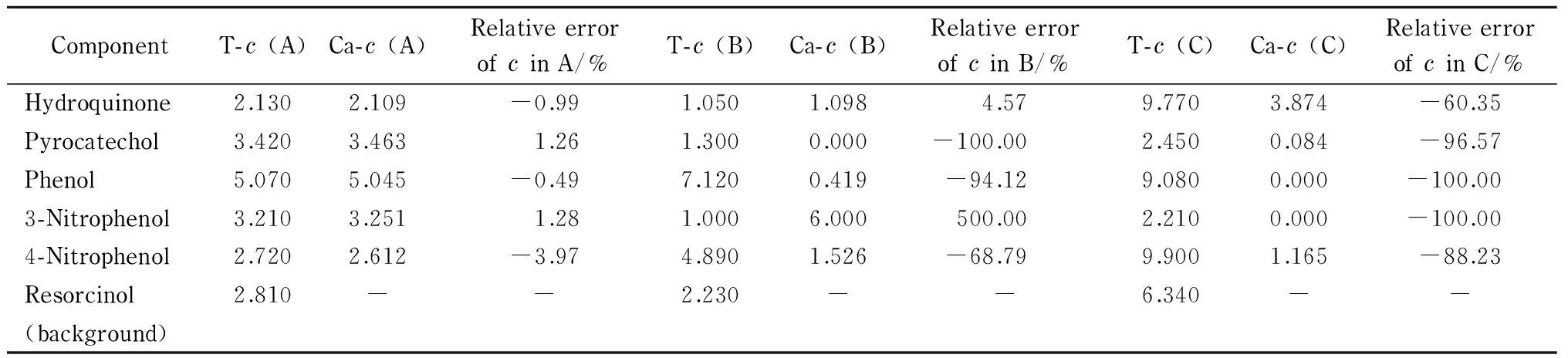
表 12 体系2的组分浓度(10-4mol/L)基于经典RAFA方法的优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

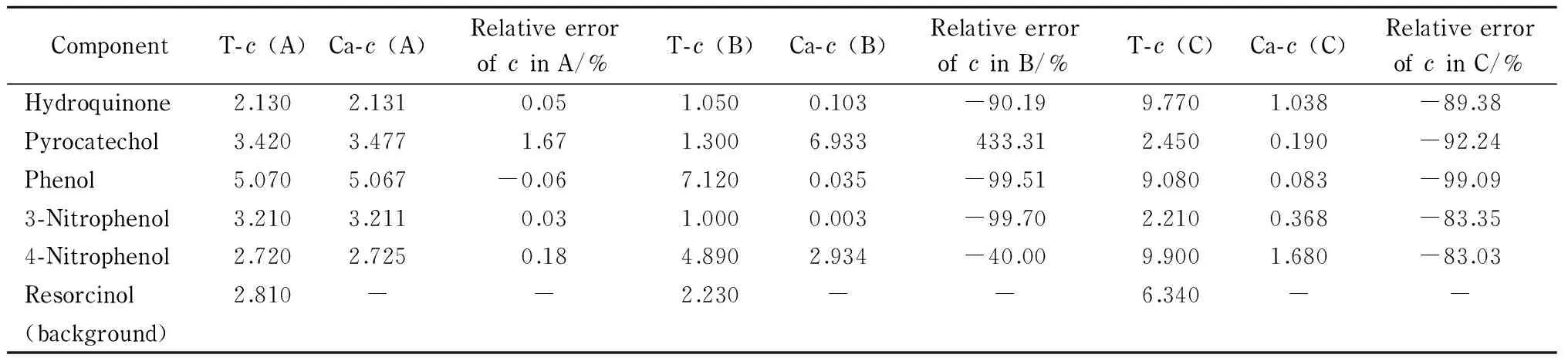
表 13 体系2的组分浓度(10-4mol/L)基于经典RBL方法的优化校正结果

A, B, and C indicate the standard and the two test solutions, respectively.

4 结论

本文力图改善约束背景双线性分解算法对二维双线性HPLC灰色分析体系的校正适用性,以使其在组分保留时间的重现性低的情况下,仍可以同时对待测组分的浓度和保留时间进行准确定量校正。本文通过模拟数据及两组实验数据验证了所建议方法的有效性。因此,本文所建议的方法有效提高了HPLC方法灰色分析体系的CBBL校正方法的准确性,对于改善矩阵校正方法在色谱灰色分析体系的适用性具有重要启发意义。

致谢 衷心感谢山西省临汾市食品药品检验所在实验工作中的大力协助。

[1] Liang Y Z, Xu Q S. Instrumental Analysis of Complex Systems——White, Grey and Black Analytical Systems and Their Multivariate Methods. Beijing: Chemical Industry Press, 2012

梁逸曾, 许青松. 复杂体系仪器分析——白、灰、黑分析体系及其多变量解析方法. 北京: 化学工业出版社, 2012

[2] Ho C-N, Christian G D, Davidson E R. Anal Chem, 1981, 53(1): 92

[3] Öhman J, Geladi P, Wold S. J Chemom, 1990, 4(2): 135

[4] Liang Y Z, Manne R, Kvalheim O M. Chemom Intell Lab Syst, 1992, 14: 175

[5] Chen W C, Cui H, Chen Z P, et al. Acta Chimica Sinica, 1997, 55(7): 693

陈文灿, 崔卉, 陈增萍, 等. 化学学报, 1997, 55(7): 693

[6] Zhang Y. Chemom Intell Lab Syst, 2015, 149: 73

[7] Lu P Z, Dai C Z, Zhang X M. Basic Theory of Chromatography. Beijing: Science Press, 1997

卢佩章, 戴朝政, 张祥民. 色谱理论基础. 北京: 科学出版社, 1997

[8] Goicoechea H C, Calimag-Williams K, Campiglia A D. Anal Chim Acta, 2012, 717: 100

[9] Elcoroaristizabal S, Juan A D, García J A, et al. Chemom Intell Lab Syst, 2014, 132: 63

[10] Vandeginste B G M. Chemom Intell Lab Syst, 2015, 149: 118

[11] Wu H L, Li Y, Yu R Q. J Chemom, 2014, 28(5): 476

[12] Li Z F, Xu G J, Wang J J, et al. Chinese Journal of Analytical Chemistry, 2016, 44(2): 305

李正风, 徐广晋, 王家俊, 等. 分析化学, 2016, 44(2): 305

[13] Xing Y N, Feng A H, Ye L Q, et al. Chinese Journal of Chromatography, 2016, 34(3): 346

幸苑娜, 冯岸红, 叶淋泉, 等. 色谱, 2016, 34(3): 346

[14] Pan Z X, Si S Z, Nie S Z, et al. Factor Analysis in Chemistry. Hefei: University of Science and Technology of China Press, 1992

潘忠孝, 司圣柱, 聂圣哲, 等. 化学因子分析. 合肥: 中国科学技术大学出版社, 1992

Scientific Research Fund From Shanxi Province, China (No. 2010011013-2); Research Project Supported by Shanxi Scholarship Council of China (No. 2014-045); Research Fund for Teaching Reform from Shanxi Normal University (No. SD2013JGXM-54).

An improvement of the calibration results for grey analytical system in high performance liquid chromatography applying constrained background bilinearization method based on genetic algorithm optimization strategy

ZHANG Yaxiong*, NIE Xianling

(KeyLaboratoryofMagneticMolecules&MagneticInformationMaterials,MinistryofEducation,SchoolofChemistryandMaterialScience,ShanxiNormalUniversity,Linfen041004,China)

Constrained background bilinearization (CBBL) method was applied for multivariate calibration analysis of the grey analytical system in high performance liquid chromatography (HPLC). By including the variables of the concentrations and the retention time of the analytes simultaneously, the standard CBBL was modified for the multivariate calibration of the HPLC system with poor retention precision. The CBBL was optimized globally by genetic algorithm (GA). That is to say, both the concentrations and the retention times of the analytes were optimized globally and simultaneously by GA. The modified CBBL was applied in the calibration analysis for both simulated and experimental HPLC system with poor retention precision. The experimental data were collected from HPLC separation system for phenolic compounds. The modified CBBL was verified to be useful to prevent the inherent limitation of the standard CBBL, which means that the standard CBBL may result in poor calibration results in the case of poor retention precision in chromatography system. Moreover, the modified CBBL can give not only the concentrations but also the retention time of the analytes. i. e., more useful information of the analytes can be generated by the modified CBBL. Subsequently, nearly ideal calibration results were obtained. On the other hand, comparing with the calibration results by the classical rank annihilation factor analysis (RAFA) and residual bilinearization (RBL) method, the results given by the modified CBBL were also improved significantly for the HPLC systems studied in this work.

constrained background bilinearization (CBBL) method; genetic algorithm (GA); grey analytical system in high performance liquid chromatography (HPLC); improvement for multivariate calibration methods

10.3724/SP.J.1123.2016.12017

2016-12-08

山西省自然科学基金项目(2010011013-2);山西省留学回国人员项目(2014-045);山西师大教学改革项目(SD2013JGXM-54).

O658

A

1000-8713(2017)06-0634-09

* 通讯联系人.E-mail:zhangyx@sxnu.edu.cn.