基于混沌映射的图像像素值置乱加密算法研究

汤泽军

(长沙航空职业技术学院，湖南 长沙 410124)

基于混沌映射的图像像素值置乱加密算法研究

汤泽军

(长沙航空职业技术学院，湖南 长沙 410124)

提出了一种基于混沌映射，过程可逆的图像像素值置乱加密算法，并分析了该图像加密算法的安全性问题。实验结果表明，该图像加密算法密钥空间大，对密钥初始条件敏感，有很高的灰度置乱程度，加解密速度快，适用于对互联网上的数字图象信息提供实时加密保护。

图像加密 ; 混沌 ; 置乱

利用互联网传递信息是一个主流的途径，主要原因包括：地理位置的独立性、没有时间限制、且成本低。然而，互联网在为我们提供强大的功能优势的同时，却也为那些未经授权个人留下了拦截信息的机会，他们往往在拦截之后进行恶意的复制、传播或销毁。因此，信息安全和信息保护成为一个研究热点问题。尤其是在当今图像传输与应用愈发频繁的网络环境中，图像信息安全受到了各相关行业的极大关注。图像加密算法正是用于解决这一问题的。其中，图像置乱加密算法即对原图像中的各像素值进行置乱而得到一副无序的不可辨认的新的图像。比较成熟的经典加密算法如 Arnold 变换， 约瑟夫遍历[1,2]等，能比 传统的密码理论更好地加密图像。但是，这些算法仅考虑位置置乱加密，像素值的大小并没有改变[3]。考虑到原始图像和加密图像的统计特性，这些算法的加密强度仍不够理想。

1989 年，英国数学家 Matthews 最早提出混沌系统用于数据加密的思想。由于混沌加密算法具有对初始条件敏感，非周期，不收敛和控制参数等特点。考虑到简单性和高安全性，许多 研 究 者 采 用 一 维 混 沌 系 统 来 改 善 算 法[4-6]。另有一些研究者基于几个经典的映射，使用高维动力系统，所有的研究主要是为了增加参数以提高安全性[7]。一个好的加密方法是应该对密钥极其敏感,密钥空间足够大，而且，它必须有一定的能力来抵御外部攻击的统计分析，即灰度分布[8]。然而，增加参数会影响到实施和提高计算复杂度，例如，使用多于一个加密算法也会降低图像加密的效率。

本文提出的基于混沌映射的图像像素值置乱加密算法，具有独特的显著特征，例如初值灵敏度初，控制参数多，能有效地排列替换像素原始图像的位置。同时根据像素比特实现灰色分布加密，该算法可进一步地增强加密强度，提高加密的安全性。

1 混沌映射和其独特的性质

经典的混沌系统，可以通过公式（1）来定义：

其中，0 ≤ μ ≤ 4，且 Xk∈ (0,1)。

从混沌动力系统来看，如果 3.569945≤μ≤ 4，混沌映射变得混乱，也就是说，对于给定的两个初值，混沌序列是非周期，非收敛和伪随机的。

例 如，μ=3.7606，x0=0.3456，y0=0.5678，混 沌现象如图1所示。

图1 混沌现象 (a) x0=0.3456 和 (b)y0=0.5678

关于混沌的定律列举如下。

定律1：混沌系统产生的序列的概率密度如下：

定律2：混沌序列离散点的平均值为

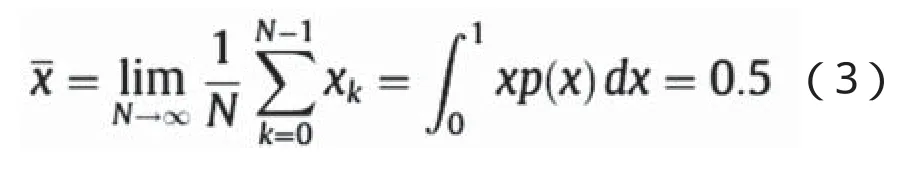
定律3：混沌序列的自相关度为

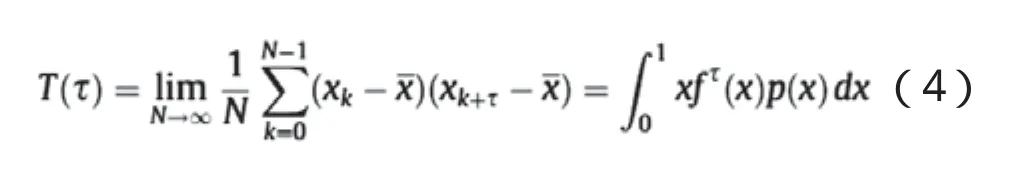
定律4：两个混沌序列的相关函数为

2 基于混沌映射提出的图像加密算法

2.1 图像加密算法

对于一幅大小为 M*N灰度图像，它是一个M 行 N 列的数字矩阵其值的范围从 0 到 255。在使用加密混沌映射的过程中，首先，N +1 地址TM 和 TN1…TNN 由混沌映射迭代生成。下一步就是使用向量 TM 来交换行，并使用向量 TN 来交换列。所以像素点的位置被完全打乱了。为了降低计算复杂度和节省时间，只用2个变换向量分别打乱行和列。

2.2 混沌序列的产生

给定一个初始 u 和 x0 和一个正整数 m，可由上面的公式得到一个无穷混沌序列。那么对于生成的序列，从中取出M个数并对它们进行排序。从排列的过程，我们可以得到变换位置向量TM。同理，我们可以得到向量 TN。

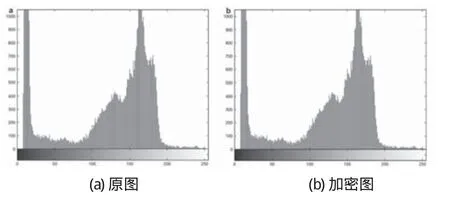
图2 直方图

2.3 加密算法与加密步骤

在新的算法中，基于混沌的图像加密结合像素位。考虑的参数数量和计算的复杂性，使用混沌映射加密，它直接施加在位置加扰加密;具有相同的加解密时间，把像素值分解为二进制位，让 P(i,j)表示原图第 i行第 j列的像素点，对其分解得到

所以，用式（6），我们可以把一幅灰度图转换成由0和1组成的二进制位矩阵。相反的，我们同样可以把二进制矩阵转换成像素点值，公式如下：

对于一张M×N大小的8位灰度图片，用上面的第一个方程得到M×8N的矩阵。对其加密后得到的二值矩阵同样是 M×8N，然后再用上面第二个方程得到M×N的加密图像。

加密过程中使用的新算法的灰度图像，解密为加密的逆过程，加密过程根据以下步骤进行：

第一步，读取一张灰度图，并表示成M×N的矩阵A。

第二步，把矩阵转换成M×8N的二值矩阵B。

第三步，对二值矩阵B的行和列分别进行混沌置乱加密得到矩阵C。

第四步，把二值矩阵C转换成M×N的矩阵D。

第五步，保存矩阵 D,加密过程结束，从而得到一张加密的灰度图。

3 仿真实验

为验证算法的安全性和实用性，使用 Matlab编 程 对 算 法 进 行 实 现。 以 如 图3(a)256×256 的Lena 图像作为实验对象，以初始值 μ=3.7606，x0=0.2017 产生混沌序列。加密图像图3(b)由图3(a)获得，从图3(b)中不能找出任何涉及到原始图像有用的信息。

图3 加密与解密测试

然后用不同的参数进行仿真，验证其对加密和解密的影响，正确的密钥是：μ=3.7606，x0=0.2017。结果如图3所示，从图中可以看出，总的密钥参数有两个，同时这两个参数的取值范围很大，这符合密钥空间大的特性，从而增加了破译的难度。

4 结论

本文提出了一种基于混沌映射和像素二进制位的新的置乱加密算法，算法能同时实现位置和加密灰度值加密，可用于为互联网上的数字图像信息提供实时加密保护。对算法进一步研究还可以扩展到高维混沌映射，实现更高安全强度的图像加密。

[1]Baptista, M.S. Cryptography with chaos[J]. Phys. Lett. A, 1998, 240(1-2): 50-54.

[2]Behnia, S., Akhshani, A., Mahmodi, H., et al., A novel algorithm for image encryption based on mixture of chaotic maps[J]. Chaos, Solitons & Fract., 2008,35(2):408-419.

[3]Chung, K.L.,& L.C. Chang, Large encrypting binary images with higher security[J]. Pattern Recognition Lett., 1998,19(15):461-468.

[4]Fang, Z.Y.,& W.Q. Tong., Image scrambling algorithm based on chaos mapping[J]. Modern Comput., 2007,(10):51-53.

[5]Fang, Z.J., Lu, X., Wei, W.M., et al., Image scrambling based on bit shuffling of pixels[J]. J. Optoelectron. Laser, 2007, 18 (12): 1481-1486.

[6]Gao, T.G. & Z.Q. Chen. Image encryption based on a new total shuffling algorithm[J]. Chaos, Solitons & Fract., 2008, 38(1):213-220.

[7]Guan, Z.H., Huang, F.J., & W. J. Guan. Chaos-based image encryption algorithm[J]. Phys. Lett. A, 2005,346(1-3):153-157.

[8]Li, Y., Fan, Y.Y. & C. Y. Hao. Information hiding technology based on image second-scrambling[J]. J. Image Graph. 2006,11(8):1088-1091.

［编校：杨 琴］

Image Scrambling Encryption Algorithm based on Chaotic Mapping

TANG Ze-jun
(Changsha Aeronautical Vocational and Technical College, Changsha Hunan 410124)

An image encryption algorithm based on chaotic mapping is presented in this paper. The paper designs a method of key generation and analyses the security of the proposed image encryption. The results show that the map can encrypt compressed images or arbitrary length of data sets and that the image encryption algorithm has a perfect hidden ability and it is suitable for the safety of digital image information on the actual Internet protection.

image encryption; chaotic; scrambling

TP309

A

1671-9654(2017)02-0090-03

10.13829/j.cnki.issn.1671-9654.2017.02.022

2017-04-17

汤泽军 (1980- )，男，湖南益阳人，讲师，工学硕士，研究方向为嵌入式系统智能测试仪表。