三维模型下永磁轨道上超导体临界电流对磁悬浮力影响研究

芦 逸 云

(洛阳理工学院 电气工程与自动化学院，河南 洛阳 471023)

三维模型下永磁轨道上超导体临界电流对磁悬浮力影响研究

芦 逸 云

(洛阳理工学院 电气工程与自动化学院，河南 洛阳 471023)

采用数值计算方法对高温超导(HTSC)块材电磁场进行模拟，计算了永磁轨道(PMR)上方超导块材所受到的磁悬浮力。文中给出了一种3D数值计算。模型采用了电磁场磁矢量法(H-方法)；基于Fortran语言开发平台编写了有限元求解代码；使用E-J幂指数模型来描述高温超导块材的电场强度E和电流密度J的关系；采用Kim模型来描述高温超导块材的临界电流密度Jc；使用了两块虚拟超导块材叠加的方法处理高温超导材料临界电流密度各向异性的特性。采用文中描述的数值计算方法，成功地对由一个永磁轨道和一块高温超导块材组成的磁悬浮系统进行了计算研究，研究了磁悬浮系统中超导块材的临界电流密度对磁悬浮力的影响。

超导; HTSC；三维模型；数值模拟

高温超导块材能够很稳定地悬浮(或者悬挂)在永磁体上方(或者下方)。这种内在的自稳定悬浮(或者悬挂)特性使得无摩擦轴承、储能飞轮和自稳定磁悬浮传输系统的潜在运用成为可能[1-2]。为了优化设计这些设备的性能，很有必要对高温超导块材的电磁特性进行模拟计算。由于YBCO块材内部存在仔晶边界效应，其内部临界电流密度沿a-b面的大小是电流密度沿c-轴的两倍。对于其E-J本构关系，与常导体的描述完全不相同。E-J幂指数假定电场强度E是与电流密度J的幂指数紧密相关的。Kim 模型假定高温超导块材的临界电流密度Jc不仅仅与该位置的电密度J相关，还和该位置的磁场强度大小相关， 这些是高温超体的E-J非线性特性和高温超导材料非线性特性。由于高温超导体的这些电磁强非线性特性，很难用数值的方法来模拟高温超导体的电磁特性。

在最近这些年，针对此类电磁问题，出现了一些数值计算方法和解析计算方法。对于2D模型，局限于与其相关的简单几何模型以及在各向同性的假设下和轴对称外磁场的假设下，研究者提出了几种解析计算方法[3-5]。对于3D模型，由于很难处理高温超导体的电磁非线性特性和受限于电脑运算能力，很少有相关报到见诸。

本文给出了一个基于有限元方法的3D模型，运用此数值模型对高温超导电磁特性进行了模拟计算。模型使用了两块虚拟超导块材叠加的处理方法来解决非线性材料问题。模型中使用了一种迭代的方法用于迭代求解E-J非线性特性，还使用了向前差分法用于处理时间空间问题。有限元求解代码是在FORTRAN语言平台下编写的。

运用文中给出的3D模型研究了由高温超导块材与永磁轨道组成的磁悬浮系统中超导块材的临界电流密度对磁悬浮力的影响。仿真计算的结果显示了超导块材的临界电流密度的增加能够增加最大磁悬浮力，并且最大磁悬浮力的增加幅度受到超导块材所受到的外磁场大小的限制。

1 基本方程

本节介绍描述高温超导块材电磁特性的基本方程。考虑一个高温超导三维几何块材模型Ω1 和非超导区域Ω2 ，如图1所示。

图1 三维超温超导模型图

Maxwell 安培定律和法拉第电磁感应定律:

×H=J,。

(1)

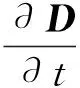
B=μH。

(2)

对于高温超导体，其E-J本构关系可描述为：

(3)

其中：Esc、Jsc和Hsc分别是高温超导块材的电场强度、电流密度和磁场强度。 Ec0是描述材料特性的一个温度相关常数， Jc是高温超导块材的临界电密度。

临界电流密度是磁场强度相关的，可以由Kim模型来描述:

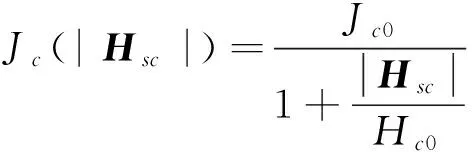
(4)

其中： Jc0和Hc0分别是与材料特性和温度相关的常数。

为了简化微分方程的推演过程，我们使用了虚拟欧姆定律：

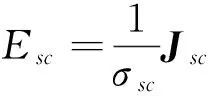
(5)

其中：σsc是高温超导块材的有效电导率：

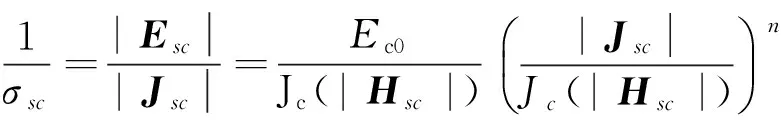
(6)

对于高温超导三维模型的非线性材料问题，研究认为沿c-轴的临界电流密度Jc是沿a-b面临界电流密度的三分之一。我们假定沿c-轴流动的电流密度所受到的电阻率三倍于沿a-b平面流动的电流密度所受到的电阻率。方程(5)又可以写成：

(7)

将方程 (1) 和方程 (2) 代入方程 (7)，可以得到：

(8)

高温导块材数学上由两部分组成，一部分是由各向同性超导材料组成，另一部分是由仅由沿c-轴方向电导率不为零的超导块材组成。

着眼于所有计算区域的超导及非超导区域，将方程(1) 代入方程 (8) ，并且考虑到Jscy=∂Hx/∂z-∂Hz/∂x,于是方程(8)可以写成如下方程：

(9)

其中：σ=σair,λ=0是指子区域Ω2；σ=σsc,λ=1 是指子区域Ω1 (见图1)； 并且定义矢量Q为Q=[0 2(∂Hx/∂z-∂Hz/∂x) 0]T。

式(9)是一个含时间变化参量的电磁偏微分方程，它是由法拉第电磁感应定律，安培定律和E-J幂指数关系式推演而出的。磁场H的分量Hx、Hy、Hz是待求解量。

对于描述某具体物理现象的偏微分方程，要想得到稳定的定解，必须给出合适的边界条件。对于控制方程(9), Dirichlet 和 Neumann 边界条件用于描述这里的电磁边界条件。在超导区Ω1与非超导抗磁区Ω2交界处的边界应该满足连续边界条件：

μ1H1n=μ2H2n。

(10)

计算区域的最外边界Ω2 属于动态边界条件。这里使用一个时间相关的函数来描述：

HΩ2(r,t)=fΩ2(r,t)。

(11)

函数fΩ2(r,t)描述了高温超导块材外界的非均匀磁场在边界Ω2处随时间的变化而变化。

2 数值求解过程

本文中使用有限元方法(FEM)和有限差分方法来建立数值求解代码，进而对此高温超导块材电磁非线性强耦合问题进行求解。

模型中使用了直接迭代方法来处理非线性偏微分方程(9)，如下所示：

(12)

其中：上标 i(i=1,2,…)暗示了迭代步骤； 下标 n 暗示了时间空间推演步骤。Hn-1是时间推演的第n步骤时的稳定解；时间变分△t指明了时间推演步每次迭代时的时间步大小。当前计算区域位于超导区域时，有效电导率σ和参数λ满足：σ=σsc和λ=1。

方程(12)又可以变换为：

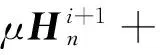
(13)

模型中使用四面体单元对计算区域进行离散剖分处理。这些属于外边界上的单元结点上的值由于属于边界条件方程(11)描述，由方程(11)计算得出。代数方程组可由下面矩阵表达式描述：

(14)

其中：[A]和[C]分别是方程(14)第二项和第三项的系数矩阵。[I]是方程(14)第一项相关的单位矩阵。[F]是与Hn-1相关的负载列向量。很明显，矩阵[A]和[C]是与有效电导率σsc紧密相关的。

数值求解的主要过程可以很简明地由下面所描述：

步骤1: 最开始，对方程(14)初始化初值如下所示：

t=0:H=H0,HΩ2(r,t=0)=fΩ2(r,t=0)。

(15)

赋于超导块材内电导率σsc非常大的初始值，这意味着当高温超导块材在初始迭代步骤时屏蔽电流密度几乎等于0。

步骤2:t=t+dt,n=t,i=1。

步骤3: 计算刚度矩阵[A]、[C]和[F],求解列向量矩阵[Hi+1] 的值。

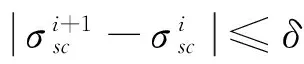
(16)

δ是一个给定的值，用于控制/横量迭代精度。如果超导块材中所有的剖分节点都满足表达式(16)，则执行式(16),then[Hi]=[Hi+1] ,i=i+1,gotoStep3。

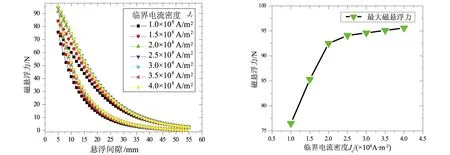
步骤5: 如果n

当计算出来磁场强度和电流密度分布后，高温超导块材所受到的磁悬浮力可以由下式计算得出：

Fem=∫vJ×Bexdv。

(17)

其中： v代表高温超导块材的体积；J是电流密度；Bex是高温超导所受到的外磁感应强度。求解代码的有效性已由实验验证[6]。

图2 高温超导块材与永磁轨道组成的磁悬浮系统

3 结果与讨论

基于文中描述的数值求解器，研究了永磁轨道上方高温超导块材内临界电流密度对磁悬浮力的影响。由永磁轨道和高温超导块材组成的磁悬浮系统简图如图2所示。其中永磁轨道是由横截面为40mm宽、40mm高的NdFeBs构成。永磁轨道的两个NdFeB的磁化方向向对排列。永磁轨道的横截面平行于x-y平面，其尺寸为宽90mm、高40mm。由永磁轨道感生出的磁场在x-y平面内呈现对称分布。

图3 磁感应强度在永磁轨道上方5 mm处竖直方向和水平方向上的分布图

模型中永磁轨道感生的磁感应强度可以使用等效电流平面解析模型计算。永磁轨道上方5mm处磁感应强度的分布图如图3所示。

磁悬浮系统中的高温超导块材尺寸是边长为30mm、厚为15mm。通过以下这种方法进行模拟计算出样品的磁悬浮力-位移恢复曲线:超导样品在永磁轨道正上方沿竖直方向由位置A以1mm/s的速度向下向位置B移动。当超导样品到达位置B后，又以同样的速度返回向位置A处移动。当高温超导块材的磁感应强度分布采用本文描述的方法计算出来后，块材样品内部的电流密度分布就可以通过数学公式(1)计算得出。最后可以依照公式(17)将超导样品的磁悬浮力计算出来。

超导样品在不同临界电流密度Jc情况下磁悬浮力-位移曲线图如图4所示。从图中可以看出，超导样品的磁悬浮力-位移磁滞恢复曲线展示了一些典型的磁滞特性。这是因为高温超导体材料的磁滞特性决定的。当超导块材沿竖直方向向下移动到永磁轨道表面处，然后又返回向上离开永磁轨道，不同的临界电流密度对应的磁悬浮力-位移磁滞恢复曲线所围的面积也不相同。从图4可以看出，磁悬浮力-位移磁滞恢复曲线所围的面积随着临界电流密度Jc的增加而减少。这是因为，当超导块材的临界电流密度较低时，样品受到外磁场的作用，磁场更容易穿透到超导块材内部。

为了更加清楚地显示出超导样品最大磁悬浮力与样品的临界电流密度Jc的关系，将最大磁悬浮力与临界电流密度曲线绘制到同一图中，如图5所示。从图中可以看出，磁悬浮力最大峰值随着临界电流密度从1.0×108A/m2到2.0×108A/m2逐渐增加时，呈线性迅速增加。当临界电流密度大于2.0×108A/m2后,磁悬浮力最大峰值随着临界电流密度的增加开始变的缓慢增加。

图4 不同电流密度下磁悬浮力-位移曲线 图5 不同临界电流密度下超导块材最大悬浮力曲线

通过对YBCO块材磁悬浮力数值计算结果可以得出：当增强超导块材材料特性(通常提高临界电流密度)时，可以在一定范围内提高超导块材的最大磁悬浮力值。最大悬浮力的增加幅度受到外界应用磁场的限制。

4 结 语

基于磁矢量方法(H-方法)和有限元方法，成功地在FORTRAN平台开发出了一个3D-模型数值计算代码，此数值计算模型着眼于高温超导电磁场的模拟计算。使用此数值计算系统，研究了高温超导块材不同临界电流密度对磁悬浮力的影响。数值模拟计算显示了增强超导块材内部临界电流密度可以提高最大磁悬浮力，但是最大磁悬浮力提高的幅度受到外磁场的限制。

[1] John R H.Applications of high-temperature superconductors in power technology[J].Phys,2003(66):1865-1886.

[2] Murakami M.Progress in applications of bulk high temperature superconductors[J].Phys C,2000,341:2281- 2284.

[3] Brandt E H.Superconductors of finite thickness in a perpendicular magnetic field:strips and slabs[J].Phys Rev B,1996,54(6):4246-4264.

[4] Prigozhin L.The Bean model in superconductivity:variational formulation and numerical solution[J].Journal of Computational Physics,1996,129:190-200.

[5] Qin M J,Li G,Liu H K,et al.Brandt,Calculation of the hysteretic force between a superconductor and a magnet[J].Phys Rev B,2002,66:024516.

[6] Lu Y Y,Wang J S,Wang S Y,et al.3D-Modeling Numerical solutions of electromagnetic behavior of HTSC bulk above permanent magnetic guideway[J].J Supercond Nov Magn,2008,21:467-472.

Effect of Superconductor with Critical Current Above PMR on Levitating Force Based on 3D-modeling

LU Yiyun

(Luoyang Institute of Science and Technology, Luoyang 471023, China)

In this paper, the electromagnetic field simulation of the high-temperature superconductors (HTS) bulk was carried out and the magnetic force between the permanent magnet railway (PMR) was calculated. Based on finite element method, a 3D-modeling numerical calculation method is described. The models were formulated with the magnetic field vector (H-method). The resulting codes were developed with FORTRAN platform. The electric field intensity E and the current density J constitutive relation of HTS were described with E-J power law. Kim macro-model was used to describe critical current density Jc of HTS bulk. Two virtual HTS bulks were used to solve the critical current density Jc anisotropic properties of HTS materials. A superconducting levitation system composed of one HTS bulk and PMR was successfully investigated using the proposed method. By this method, the influence of critical current density on magnetic levitation force of the superconducting levitation system was mathematically studied.

superconductor; HTSC; 3D model; simulation

2017-01-06

芦逸云(1972-)，男，新疆温泉县人，博士，副教授，主要从事超导电磁理论及应用方面的研究。

国家青年自然基金项目(11205080).

10.3969/i.issn.1674-5403.2017.02.022

O441;TM12

A

1674-5403(2017)02-0083-05