基于改进型有限控制集模型预测的永磁电机直接转矩控制

陈令荣，李 强，储建华

（1．江苏省徐州技师学院，徐州221151；2．东南大学，南京210096）

0 引 言

近年来，永磁同步电机（以下简称PMSM）在电力传动系统，尤其是电动汽车中使用广泛，主要是因为其具有较大的能量密度和较高的效率［1－3］。在PMSM驱动系统中，为了获取更快的转矩响应，多采用直接转矩控制（以下简称DTC），它不同于磁场定向控制的地方在于没有电流闭环，所以响应更快。传统的DTC控制策略是基于2个非线性滞环调节器和开关状态表实现的，因此导致了开关频率不固定和转矩脉动的问题［4－6］。

为了减少电流纹波和转矩脉动，文献［7－8］提出了一种结合空间矢量脉宽调制（以下简称SVPWM）和DTC的控制策略，控制中引入了PI转矩闭环来计算电压参考，进而通过SVPWM生成固定开关频率的脉冲，进而减小电流和转矩脉动，但是PI控制器的引入降低了DTC控制的响应速度。与此同时，随着预测控制技术和数字芯片的发展，高性能转矩控制策略得以实现，例如转矩预测控制和模型预测控制［9－13］。其中转矩预测控制根据PMSM模型和需要的转矩，用预测的方法计算定子电压参考［9－10］，结合使用SVPWM 得到固定的开关频率，进而降低转矩脉动，但是其难以考虑系统约束，例如电流限制等。文献［14－16］提出了一种无差拍DTC控制策略，兼顾了较快的响应速度和较低的转矩脉动，但是计算复杂度高，难以低成本工程应用。而有限控制集模型预测控制（以下简称FCSMPC）由于使用了由开关矢量构成的有限控制集，同时还构建了考虑系统约束的成本函数，故通过穷举法可以得到使成本函数计算值最优的开关矢量。该方法的一个主要优点是通过构建成本函数，可以考虑不同系统约束下提高控制性能［17］。因此，FCSMPC可以实现DTC和特殊控制目标结合，例如最大转矩电流比（以下简称 MTPA）［18－19］。但是 FCSMPC也存在DTC控制固有的问题，即不固定的开关频率将导致较大的转矩脉动。为此，文献［20］提出了一种基于FCSMPC的转矩脉动补偿方案，但是其出发点是基于电机模型精细化，没有考虑由变频器导致的转矩脉动。

本文基于上述研究，设计了一种基于改进型有限控制集模型预测的PMSM直接转矩控制策略，控制方案中引入了最优占空比的概念，同时考虑了MTPA。新型控制策略结合了FCSMPC和李亚普洛夫理论，构建了同时兼顾转矩跟踪，MTPA和其他系统约束的成本函数。同时还采用了李亚普洛夫函数来计算有限控制集中的电压矢量占空比。最后，搭建了PMSM驱动试验平台，对新型FCSMPC控制策略的有效性进行了试验验证。

1 d－q坐标系下的PMSM模型

改进FCSMPC的DTC控制是基于同步旋转d－q坐标设计的，其中PMSM在d－q坐标系下的模型［12］：

式中：R，Ld，Lq和ψf分别为定子电阻，d，q轴定子电感和电机永磁磁链；p是电机极对数；ud和uq分别为d，q轴定子电压；id和iq分别为d，q轴定子电流；ω为电角频率。使用前向欧拉算法离散后的PMSM模型：

式中：T为一个较小的时间间隔，其小于或等于采样时间；k为当前步长。PMSM的输入电压由驱动变频器给出，udq，k＝［ud，k，uq，k］T。对于两电平变频器，其输出开关矢量一共有8种不同的开关状态组合，即｛（Sa，Sb，Sc）｜Sa，b，c∈｛0，1｝｝，其中Sa，Sb和Sc分别为ABC三相的开关状态。根据文献［21］和等幅值Par k变换，变频器输出电压矢量在d－q坐标系下的方程：

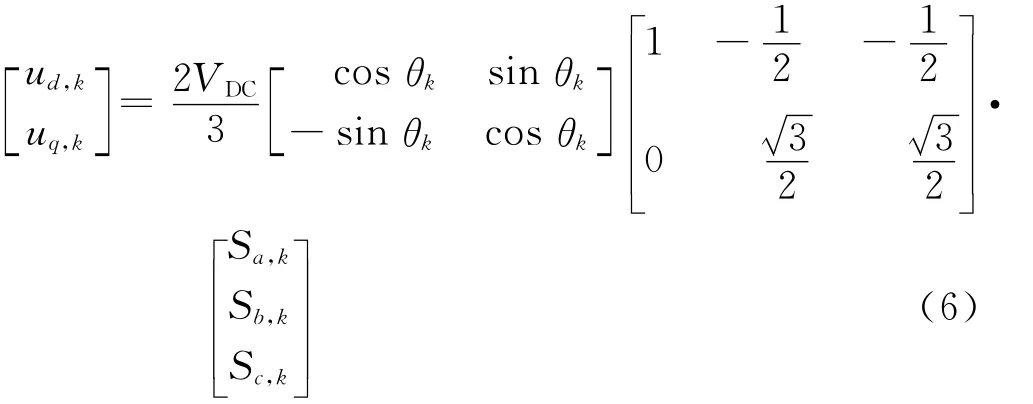
8个开关状态000，001，…，111将生成8个电压矢量，故但考虑到开关状态000和111将生成相同的电压矢量，故最后用于控制的有限控制集为｛｜j＝1，2，…，7｝。

2 基于改进FCSMPC的直接转矩控制

为了最大限度地减少电流纹波和转矩脉动，基于李亚普洛夫在设计了改进型FCSMPC直接转矩控制控器，具体的控制器框图如图1所示。从图1中可以看出，控制器中包含了单步长电流赋值算法、基于李亚普洛夫的占空比计算和成本函数计算等。

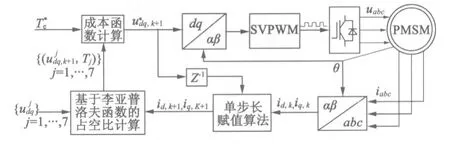
图1 基于改进FCSMPC的直接转矩控制框图

1． 1单步长赋值算法

在数字处理器中，由于参考电压矢量的计算需要时间，所以计算得到的参考电压不能及时实施，需要延迟到下一个采样周期，具体的延时示意图如图2（a）所示。其中下标k代表了当前采样，tc为参考电压的计算耗时，xk为当前采样值（电流或转矩），是基于xk计算而来的。由于计算耗时，将在下一个采样间隔k＋1实施。在这种情况下，将不再是采样间隔k＋1的最优参考电压，这是引起转矩脉动的部分原因［22］。

为了减少数字处理器采样延迟导致的转矩脉动，设计了单步长赋值算法，具体示意图如图2（b）所示。图中tc1代表了变量赋值时间，基于测量得到的xk和PMSM模型，可以得到第k＋1个采样周期的状态。然后基于更新状态，用预测控制器计算后，在tc2时刻得到最优参考电压，进而在第k＋1个采样周期能够及时的实施，即实施最优的参考电压。单步长赋值算法的执行方程：

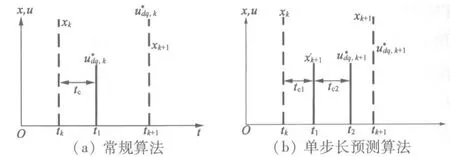
图2 数字处理器延迟原理

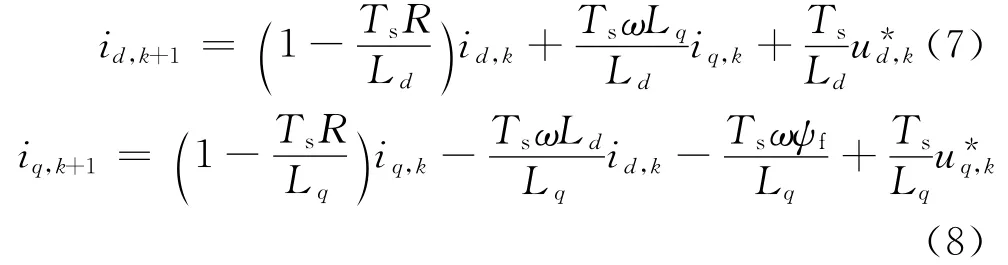
上式 中 电 流id，k＋1和iq，k＋1将 用 于 预 测 计 算，电 压和在上一个步长得到。而估计转矩可以由式（3）计算得到。

1． 2 FCSMPC的成本函数构建

为了实现MTPA条件下的转矩控制，构建了一个考虑转矩跟踪、MTPA和电流限制的成本函数，具体方程描述如下：

式中：Np为模型预测的预测尺度，由于FCSMPC算法基于穷举所有的电压矢量，故计算量是随着Np成倍增加的。为了保证计算的实时性，通常选择Np为1。上式中kT，kA和kL为成本函数的加权系数，而JT（k）和JA（k）具体如下：

在考虑PMSM 的电流限制后，JL1（k）和JL2（k）的表达式：

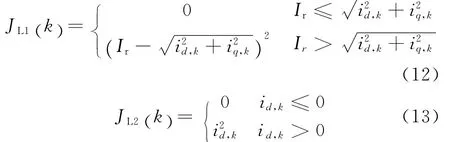
式中：Ir是PMSM的额定电流。JL1（k）为考虑电机发热的电流限制，JL2（k）是确保在MTPA条件下d轴电流收敛。通过构建成本函数，MTPA条件下的转矩控制转换为成本函数的最小化。在成本函数中，一般kL一般远大于kT和kA，以防止PMSM过电流和保证id≤0。对于kT和kA的选择，可考虑kT＋kA＝1，较大的kT将导致快速的转矩收敛，而较大的kA将使得MTPA条件快速达到。本文中设计kT＞kA，以获取更快的转矩响应。

1． 3基于李亚普洛夫函数的占空比计算

为了进一步降低转矩脉动，引入了李亚普洛夫函数对每个电压矢量的占空比进行计算。由于JL1和JL2只是限制条件，并不是全局可微的，故在基于李亚普洛夫函数的占空比计算中不考虑。具体的李亚普洛夫函数设计：

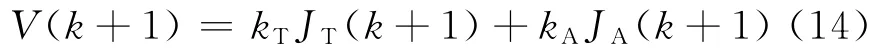
当满足V（k）＝0时，第k个采样周期的转矩，同时MTPA条件可以达到。此外，当满足d V（k）／d t＝0时，转矩和磁链将在MTPA工作点稳定，进而电流纹波和转矩脉动可以最小化。首先阐述下面3个结论：

（1）结论1：定义电流函数如下：

如果PMSM的转矩保持一个非零值，则f（id，iq）是沿恒定转矩曲线严格单调的函数。证明如下：

转矩Te＝1．5p［ψf＋（Ld－Lq）id］iq为常数，对f（id，iq）和Te求偏导数如下：

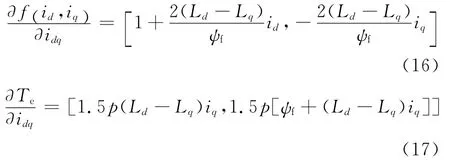
恒定转矩下，工作点沿着矢量r方向的轨迹满足r Te／idq＝0，矢量r的表达式：

式中：ε为正实数，可以注意到：

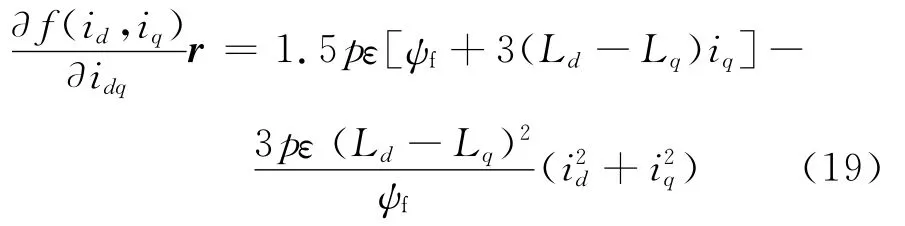
由于Ld－Lq≤0和id≤0，式（19）中等号右边项为负，因此f（id，iq）是沿恒定转矩曲线严格单调的函数。根据结论1，要保证李亚普洛夫函数严格递减，可以控制工作点轨迹如下：首先沿着恒定转矩曲线运行到f（id，iq）＝0，然后沿着 MTPA曲线运行到转矩达到参考转矩，如图3所示，从A点到B点再到C点。因此，至少存在一条工作点轨迹曲线使得李亚普洛夫函数严格递减。

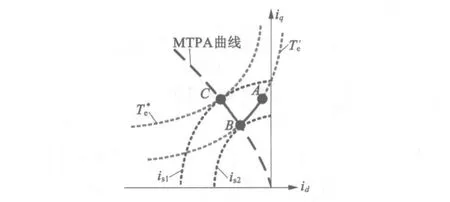
图3 满足MTPA的工作点运行轨迹

（2）结论2：对于任意初始条件，如果PMSM的反电动势在变频器输出电压限制内，那么存在一个满足d V（k＋1）／d t≤0。证明如下：

对李亚普洛夫函数求导，可得：

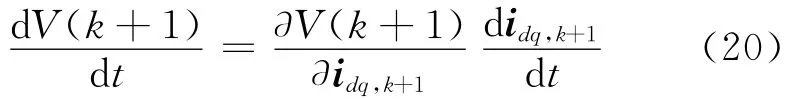
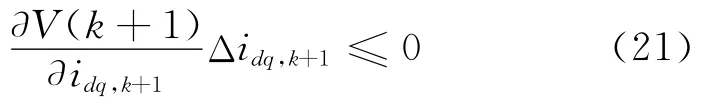
上式中等号当且仅当V（k＋1）＝0时成立，因此，存在电流微分d idq，k＋1／d t＝λΔd idq，k＋1使得V（k＋1）≤0，其中λ是一个非常小的正实数。电压u＊dq，k满足：

式中：idq，k＋1为电流矢量。由于至少存在一条工作点轨迹曲线使得李亚普洛夫函数严格递减，则存在Δidq，k＋1满足：

当uE在变频器电压限制范围内，λ可以设置为足够小来保证u＊dq，k＋1也在限制范围内，既满足d V（k＋1）／d t≤0。

（3）结论3：对于给定的电流动态：

如果PMSM的反电动势在变频器输出电压限制内，那么存在ujdq，k∈｛ujdq，k｜j＝1，2，…，7｝满足：

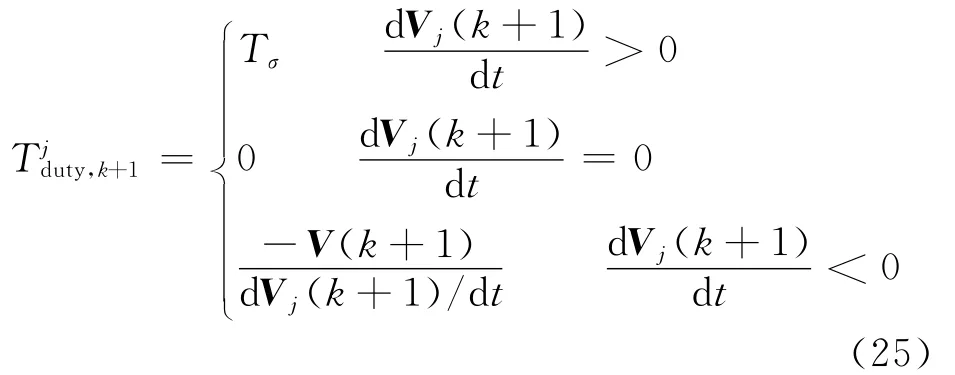
结论3的具体证明过程参考文献［23］。为了尽量减少稳态时的转矩脉动，期望李亚普洛夫函数稳态时保持V＝0和d V／d t＝0，为此电压矢量ujdq，k的占空比计算式：其中Tσ＜＜Ts为一常值，当电流达到上限时，占空比设置为Tσ，此时电流限制JL在成本函数中占主导。FCSMPC中还需考虑电压矢量Vj（k＋1）满足d Vj（k＋1）／d t≤0。当PMSM 的模型和相关预测是准确的，那么Tσ＝0是保证最小电流纹波的理想设置。但是实际系统中总是有一些诸如电机参数偏移之类的扰动，因此需要根据扰动来选择一个较小的Tσ，本文中选取Tσ＝0．1Ts以获取较高的抗扰度，实际工程中可以适当减小。

占空比计算结果Tj限制在［0，Ts］，根据结论3，在第k＋1个采样周期至少存在一个ujdq，k＋1（占空比为Tjduty，k＋1），在不考虑电流限制的情况下能保证李亚普洛夫函数V（k＋2）＝J（k＋2）收敛到0。另一方面，基于式（25）计算的占空比Tjduty，k＋1能保证稳态d V／d t＝0。因此，所有使d Vj（k＋1）／d t＜0的电压矢量都是成本函数最小化的候选矢量。故计算占空比之后，实际的有限控制集为｛（ujdq，k＋1，Tjduty，k＋1）｜j＝1，2，…，7｝。

1． 4 FCSMPC的具体实施

为了实现固定采样频率和固定开关频率，定义一个补充电压矢量如下：

补充电压矢量的使用将使d idq，k＋1／d t＝0，进而使成本函数计算结果不变。最终实施的电压矢量：

式（27）中只有作用到 PMSM 能对转矩产生影响，即保证收敛和MTPA实现，后续作用使d V／d t＝0。作用后，在第k＋2个采样周期的预测电流：

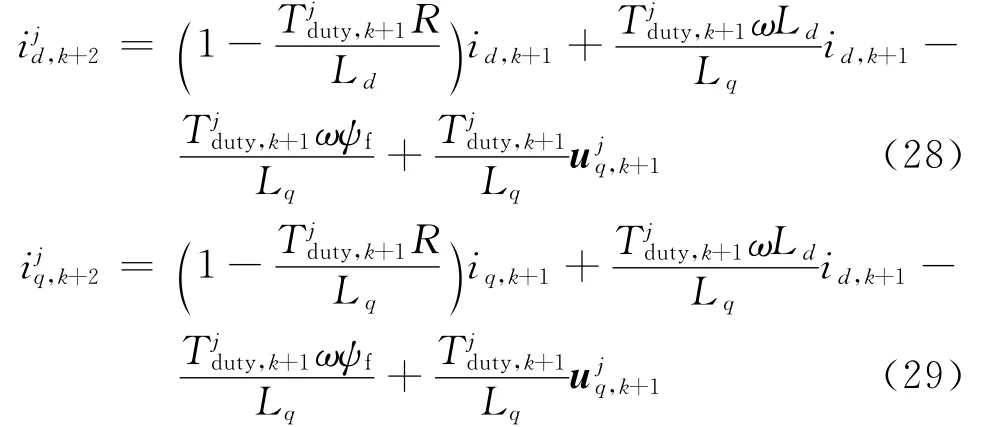
根据预测电流，基于成本函数计算在有限控制集中选取最优电压矢量：

最后的输出电压参考：

从上式中可以看出，暂态中设置最优占空比等于Ts能最小化成本函数。因此，在同样的采样频率下，新型策略策略的转矩响应和传统FCSMPC一样快。同时结论3保证了所提出的控制方案的稳定性。另一方面，稳态时补充电压矢量将保持d V／d t＝0。因此，电流纹波和转矩脉动可以最小化。

3 试验验证

为了验证所提出控制策略的实际可行性和效果，搭建了PMSM驱动试验平台开展了试验研究，试验平台如图4所示。PMSM的参数以及试验平台的主要参数如表1所示。核心算法基于实时仿真系统d SPACE（DS1103）实现，试验中控制转速在300 r／min。同时进行了新型控制策略和传统FCSMPC控制方案的对比试验，以检验其有效性。

图4 试验平台结构示意图

表1 PMSM参数和系统系统主要参数

图5和图6分别为传统FCSMPC控制方案和改进FCSMPC控制方案的试验波形。从图中可以看出，2种控制策略下的转矩响应暂态过程是近似的，但是在同样的开关频率下，改进型控制策略的转矩脉动明显减小。这个结论还可以从如图7所示的电流和转矩频谱分析图中更加准确地得到。

图5 传统FCSMPC控制方案的试验波形

图6 改进FCSMPC控制方案的试验波形

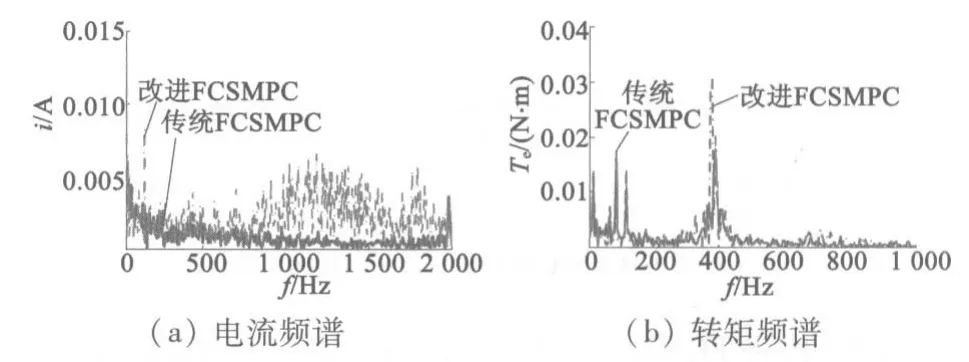
图7 2种控制方案的电流和转矩频谱分析

为了验证控制策略对电机参数误差的鲁棒性，将控制器中参数Lq设置为1．5倍Lq和参数ψf设置为1．3倍ψf，并分别进行了2组对比试验。其中图8和图9分别为传统FCSMPC控制方案和改进FCSMPC控制方案在参数Lq扰动下的试验波形；图10和图11分别为传统FCSMPC控制方案和改进FCSMPC控制方案在参数ψf扰动下的试验波形。从Lq参数扰动试验结果来看，Lq参数误差对2种控制方案的影响很小，扰动并没有改变控制器的工作点，转矩仍较为稳定地跟踪参考值，可以注意到传统FCSMPC控制方案的转矩脉动依然较大。从ψf参数扰动试验结果来看，它对控制的影响大于Lq参数扰动，这使得两种控制方案下的转矩偏离参考值，即存在一个转矩跟踪稳态误差，对比新型控制和传统FCSMPC控制，可以看出新型控制策略的误差更小，因而鲁棒性更好。因为ψf参数扰动导致了传统FCSMPC控制下的较大工作点偏移，从而选取的开关矢量不是最优的开关矢量，进而控制性能不佳。

图8 传统FCSMPC控制在参数L q误差下的试验波形

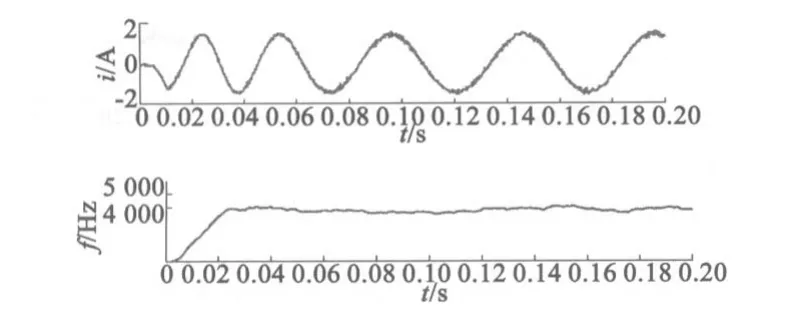
图9 改进FCSMPC控制在参数L q误差下的试验波形

图10 传统FCSMPC控制在参数ψf误差下的试验波形

图11 改进FCSMPC控制在参数ψf误差下的试验波形

4 结 语

本文提出了一种用于PMSM驱动系统的基于李亚普诺夫函数的FCSMPC控制策略。通过理论研究和试验验证，现总结结论如下：

（1）改进型FCSMPC控制策略使用了基于李亚普诺夫函数的占空比计算方案和综合考虑MTPA和电流限制的成本函数，实现了固定开关频率和电流纹波最小化。

（2）对比传统的FCSMPC控制策略，新型控制方案的转矩脉动明显降低，同时参数扰动试验验证了新型控制方案的鲁棒性更好。

（3）后续的研究方向：考虑增加基于卡尔曼滤波或自适应观测器的模型误差补偿，以进一步提高该控制策略的鲁棒性。

［1］ 李东和．纯电动汽车用永磁同步电机温度场计算［J］．微特电机，2016，44（1）：12－16．

［2］ 符晓玲，刘旭东．电动汽车用永磁同步电机滑模预测控制［J］．微特电机，2015，43（11）：53－56．

［3］ 刘奇林，沈启平．车用高功率密度永磁同步电机设计及试验研究［J］．电机与控制应用，2016，43（1）：88－94．

［4］ 薛诚，宋文胜，冯晓云．五相永磁同步电机多目标优化直接转矩控制算法［J］．中国电机工程学报，2016，36（6）：1695－1704．

［5］ 孙旭霞，高沁源，孙伟．基于SVPWM的永磁同步电机直接转矩控制系统［J］．电气传动，2016，46（11）：3－6．

［6］ 徐艳平，雷亚洲，马灵芝，沙登卓．基于模糊参数优化的PMSM反推直接转矩控制［J］．电气传动，2015，45（12）：12－16．

［7］ TANG L，ZHONG L，RAHMAN M F，et al．A novel direct torque controlled interior per manent magnet synchronous machine drive wit h low ripple in flux and torque and fixed switching frequency［J］．IEEE Transactions on Power Electr onics，2004，19（2）：346－354．

［8］ Cho Y，Lee K B，Song J H，et al．Torque－Ripple Mini mization and Fast Dyna mic Scheme f or Tor que Predictive Control of Per manent－Magnet Synchr onous Mot ors［J］．IEEE Transactions on Power Electr onics，2015，30（4）：2182－2190．

［9］ VAFAIE M H，DEHKOR D I B M，MOALLEM P，et al．A new predictive direct tor que contr ol met hod f or i mpr oving bot h steady－state and transient－state operations of PMSM［J］．IEEE Transactions on Power Electronics，2016，31（5）：3738－3753．

［10］ ZHANG Y，ZHU J．Direct tor que control of per manent magnet synchr onous motor wit h reduced torque ripple and co mmutation frequency［J］．IEEE Transactions on Power Electronics，2011，26（1）：235－248．

［11］ 王艳霞．基于模型预测的永磁同步电机直接转矩控制及负载角限制［J］．微特电机，2016，44（8）：126－130．

［12］ 牛峰，李奎，王尧．永磁同步电机模型预测直接转矩控制［J］．电机与控制学报，2015，19（12）：60－67．

［13］ 李昆鹏，万健如，朱琳．永磁同步电机瞬时功率预测控制［J］．电工技术学报，2015，30（1）：38－44．

［14］ 张明晖，杨家强，陈磊，楼佳羽．基于扩张状态观测器的永磁电机电流预测控制［J］．浙江大学学报（工学版），2016，50（7）：1387－1392．

［15］ 浦龙梅，张宏立．永磁同步电机的无差拍预测转矩控制系统［J］．电机与控制应用，2016，43（8）：21－25．

［16］ XU W，LORENZ R D．Dynamic loss mini mization using i mpr oved deadbeat－direct tor que and flux control f or interior per manent－magnet synchronous machines［J］．IEEE Transactions on Industry Applications，2012，50（2）：1053－1065．

［17］ RODRIGUEZ J，KAZMIERKOWSKI M P，ESPINOZA J R，et al．State of the art of finite control set model predictive control in power electronics［J］．IEEE Transactions on Industrial Inf or matics，2013，9（2）：1003－1016．

［18］ XIE W，WANG X，WANG F，et al．Finite－control－set model predictive torque control with a deadbeat sol ution f or PMSM drives［J］．IEEE Transactions on Industrial Electronics，2015，62（9）：5402－5410．

［19］ XIE W，WANG X，WANG F，et al．Dynamic loss mini mization of finite control set－model predictive torque control f or electric drive system［J］．IEEE Transactions on Power Electronics，2016，31（1）：849－860．

［20］ MORA A，ORELLANA A，JULIET J，et al．Model predictive torque control f or torque ripple compensation in variable speed PMSMs．［J］．IEEE Transactions on Industrial Elec－tronics，2016，63（7）：4584－4592．

［21］ MOREL F，LIN S X，RETIF J M，et al．A comparative study of predictive current control schemes for a per manent－magnet synchronous machine drive［J］．IEEE Transactions on Industrial Electronics，2009，56（7）：2715－2728．

［22］ CORTES P，RODRIGUEZ J，SILVA C，et al．Delay compensation in model predictive current control of a three－phase inverter［J］．IEEE Transactions on Industrial Electronics，2012，59（2）：1323－1325．

［23］ PRIOR G，KRSTIC M．Quantized－input control Lyapunov approach for per manent magnet synchronous motor drives［J］．IEEE Transactions on Control Systems Technology，2013，21（5）：1784－1794．