TM-Zn金属间化合物结构稳定性的第一性原理研究

方 圆，陈祖华，萨百晟，吴 波

(福州大学材料科学与工程学院，福建 福州 350116)



TM-Zn金属间化合物结构稳定性的第一性原理研究

方 圆，陈祖华，萨百晟，吴 波

(福州大学材料科学与工程学院，福建 福州 350116)

基于能带结构，提出Jahn-Teller效应的诱发条件. 基于声子色散曲线，揭示晶格动态稳定性和简并振动模式产生劈裂的物理特征. 基于电子局域化函数和束缚能，揭示原子成键特性. 结果表明，TM-Zn(TM=Ni, Pd, Pt, Cu, Ag, Au)金属间化合物发生立方到四方的相变变形过程中，结构保持稳定.

TM-Zn金属间化合物； 相变变形； Jahn-Teller效应； 结构稳定性； 第一性原理计算

0 引言

过渡金属元素中的Ni、 Pd、 Pt位于元素周期表的第10族，Cu、 Ag、 Au位于元素周期表的第11族，与Zn元素形成金属间化合物(TM-Zn)后，价电子数目多，可望具有独特的物理、 化学和力学性质[1-4]，部分金属间化合物可用作催化剂[5-6]，或用于高温结构材料和形状记忆合金[7-10]. 对于TM-Zn系金属间化合物的研究，实验上已经报道了立方CsCl型CuZn、 AgZn、 AuZn和NiZn金属间化合物，以及四方CuTi型NiZn、 PdZn和PtZn金属间化合物的存在[4, 11-20]. Shreder等[21]发现，伴随AgZn合金由立方向四方相变，吸收光谱会增加一个新的吸收峰. 最近，Chouhan等[22]计算包括了AgZn和AuZn在内的一系列Ag基和Au基金属间化合物的电子结构和弹性性质，发现具有CsCl型结构的AuZn延展性远好于AgZn. Isaeva等[7]计算作为高温结构材料的AuZn，研究其对应于横声学波的声子反常现象. 有研究还表明，具有CsCl型结构的金属间化合物在高温和应变条件下有发生由立方相向四方相变形的倾向. 这种变形改变了金属间化合物的晶格对称性，影响晶粒间位向关系，从而使材料发生断裂前能够激活滑移位错，有效提升了合金延展性[23]. 因此，晶型变化对于改善TM-Zn基材料的力学性能至关重要.

基于第一性原理计算，研究TM-Zn金属间化合物在发生“CsCl型→CuTi型”结构相变时体系的能量、 态密度、 声子色散曲线、 电子局域化函数和束缚能的变化，从电子结构层次，揭示CsCl型TM-Zn金属间化合物发生四方变形时结构稳定性的机制.

1 计算方法

基于密度函数理论的第一性原理计算方法中，利用Exact Muffin-Tin Orbitals (EMTO) 方法及全电荷密度 (Full Charge Density) 处理技术，精确地计算了体系能量，来确定体系的结构稳定性[24]. 计算中，选取GGA-PBE作为电子交换-关联泛函，使用“Frozen-core”近似求解Kohn-Sham方程. 截断能为26.53 eV，通过对分布在半球等势面上的16个能量点进行格林函数积分. 对CsCl型和CuTi型结构，在Γ对称性下分别自动生成了13×13×13和13×13×11的倒空间K点. 总能计算收敛判据选取为1×10-6eV.

运用 VASP(Vienna ab initio package) 软件包，采用投影缀加波赝势(PAW)和PBE交换-关联泛函，计算了TM-Zn金属间化合物的电子结构、 声子色散曲线和化学成键. 计算中，能量截断值设置为450 eV； 对应于CsCl型结构和CuTi型结构，K点分别为25×25×25和25×25×23，能量收敛判据设置为1×10-6eV. 使用VASP的局部弛豫技巧，模拟TM-Zn金属间化合物的四方变形过程. 即在一系列沿着 [001] 方向的拉应变εij下，CsCl型结构晶胞被迫沿着另两个方向弛豫，直到在这两个方向上应力张量σij小于0.05 GPa为止[25]. 用YPHON软件并结合线性响应理论，计算每一种金属间化合物的声子色散曲线. 计算中使用了2×2×2的超胞和13×13×13的K点. 运用VESTA软件，可视化分析了电子局域化函数.

2 结果与讨论

2.1 TM-Zn金属间化合物立方相到四方相的相变过程

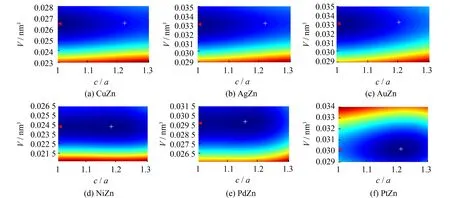
图1 TM-Zn金属间化合物等能量面Fig.1 Contour surfaces of total energy of TM-Zn intermetallic compounds calculated

上述计算结果表明，对于含有第11族元素(TM11) 的三个金属间化合物： CuZn、 AgZn和AuZn，其最稳定结构为CsCl型. 如图1所示，它们的全局能量最低(红三角箭头标记). 随着c/a比增加，四方变形程度加剧，CuZn呈现能量降低趋势，并在c/a比为1.214处存在一局域极小值点(白十字标记)，表明CuZn在四方变形过程中可得到亚稳的CuTi型结构. 对AgZn而言，这种趋势在c/a比为1.15～1.22时依然存在，但变得很弱. 而AuZn的体系能量，随着c/a比增加始终是上升的，不存在特殊的下降或平缓区域.

与TM11-Zn金属间化合物不同，对于含有第10族元素 (TM10) 的三个金属间化合物： NiZn、 PdZn和PtZn，其全局能量最低点(白十字标记)都落在c/a比为1.1～1.3的区间内. 因此，TM10-Zn金属间化合物的最稳定结构是CuTi型. NiZn和PdZn在c/a比为1.05附近出现鞍点，并都在c/a比为1处达到局域能量极小值(红三角箭头标记)，故两种金属间化合物的CsCl型结构是亚稳态的. 而PtZn的体系能量，虽随着c/a比减小，呈现出缓慢增加并在c/a比为1处出现停滞的趋势，但并未出现局部极小值.

图2 TM-Zn金属间化合物“总能-c/a比”曲线Fig.2 Etotal vs. c/a ratio curves of TM-Zn intermetallic compounds

2.2 电子态密度

为揭示TM-Zn金属间化合物由立方相向四方相变形时，变形结构的稳定性，将每一种金属间化合物沿[001]方向拉伸，选取5个不同c/a比，对比其态密度 (DOS) 变化情况，如图3所示.

图3 不同c/a比下 (c/a=1～RCuTi)，TM-Zn金属间化合物的态密度 (DOS)Fig.3 DOS of TM-Zn intermetallic compounds under different c/a ratio (c/a=1～RCuTi) with

从图3(a)、 (b)和(c)中可以看出，TM11-Zn金属间化合物在费米能级处(EF)的态密度(N(EF))基本一致，不随c/a比发生明显变化. 而TM10-Zn金属间化合物则不然，TM10-Zn金属间化合物在四方变形过程中，表现出明显的Jahn-Teller效应，如图3(d)、 (e)和(f)所示. 由于晶体结构变化，伴随着N(EF)的下降，态密度在费米能级处的大峰劈裂为两个分别对应于低能量态和高能量态的小峰. 当c/a比等于1时，它们的费米能级在态密度的峰位上； 随c/a比增加，发现N(EF)呈现出局域极小值，即Jahn-Teller效应所特有的“峰劈裂为谷”.N(EF)值的大小是判定一个结构是否稳定的重要指标，N(EF)越小则结构的稳定性越高. 这种Jahn-Teller分裂使得TM10-Zn的四方结构比立方结构更加稳定.其原因在于TM10体系比TM11体系少一个电子，从而使其费米能级下移. TM原子d轨道的变化及其分态密度所处的位置，对诱发Jahn-Teller效应起到了关键作用.

轨道能级状态对Jahn-Teller效应的影响，在能带结构中更能得以直观体现. 图4和图5为不同体系中TM原子的d轨道在能带上的投影(分能带结构). 图4中费米能级已扣除，红带、 青带和黄带分别表示TM11元素的p,eg和t2g电子对能带的贡献，图5中费米能级已扣除，红带、 青带和黄带分别表示TM10元素的p,eg和t2g电子对能带的贡献. 青色圆片带表示TM原子的eg轨道所占据的能带位置； 黄色圆片带表示TM原子的t2g轨道所占据的能带位置. 其中，eg轨道是由dZ2和dX2-Y2轨道的二重简并而来，而t2g则是由dXY、dYZ和dZX轨道的三重简并而来. 当CsCl型结构转变为CuTi型结构时，TM11-Zn金属间化合物也像TM10-Zn金属间化合物一样发生了简并轨道的劈裂. 特别是TM原子的eg轨道劈裂为高能级的dX2-Y2轨道和低能级的dZ2轨道. 虽然四方变形均导致了结构对称性的降低以及简并轨道的劈裂，但并不是所有金属间化合物都能诱发Jahn-Teller效应.

图4 CsCl型和CuTi型TM11-Zn金属间化合物的分能带结构Fig.4 Partial band structures of CsCl-type structures and CuTi-type structures of TM11-Zn

图5 CsCl型和CuTi型TM10-Zn金属间化合物的分能带结构Fig.5 Partial band structures of CsCl-type structures and CuTi-type structures of TM10-Zn

在图4中，对于所有TM11-Zn金属间化合物，其费米能级都远离TM原子的d轨道. 因此，通过简并轨道劈裂改变总能的程度有限. 相反，TM10体系少了一个电子，使费米能级下降到刚好落在CsCl型结构所对应的eg轨道上. 当四方变形发生，更低能级的dZ2轨道被占满，更高能级的dX2-Y2轨道被空出. 这导致了总电子能量的降低，使CuTi型结构能够稳定存在. 图5为此提供了直接的证据.

总之，TM-Zn金属间化合物具有Jahn-Teller效应的两个特征： (1) 结构在发生变形后能够诱发简并轨道的劈裂； (2) 费米能级EF位于简并轨道附近.文献中所报道的其他金属间化合物体系，例如MoNb、 TaTr、 IrTi和LaCd等，也具有上述特征[23, 26-28].

2.3 声子色散曲线及动态晶格稳定性

为阐明TM-Zn金属间化合物在四方变形过程中温度对晶格稳定性的影响，计算沿第一布里渊区中高对称点路径的声子色散曲线，如图6和图7所示.

图6 TM11-Zn的CsCl型和CuTi型结构声子谱Fig.6 Phonon spectrums of CsCl-type structures and CuTi-type structures of TM11-Zn

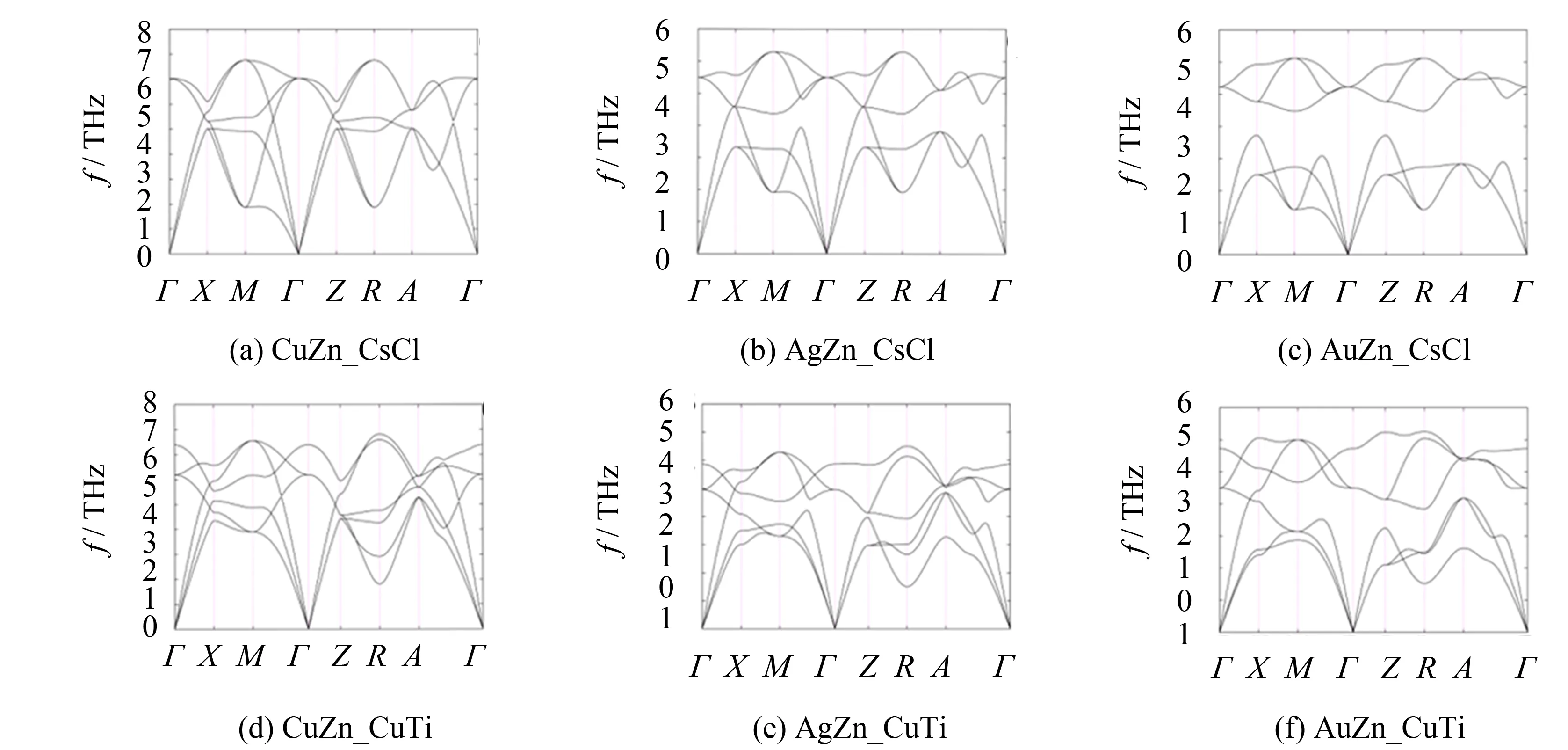
图7 TM10-Zn的CsCl型和CuTi型结构声子谱Fig.7 Phonon spectrums of CsCl-type structures and CuTi-type structures of TM10-Zn

TM-Zn金属间化合物原胞中包含有两个原子，因此产生了振动模式的六条分支，其中有三条对应于低频声学模式，另外三条对应于高频光学模式. 这些分支又可以细分为四类，即： 横声学波 (TA)、 纵声学波 (LA)、 横光学波 (TO) 和纵声学波 (LO). 随着TM与Zn的原子质量比增加，光学波逐渐远离声学波. 因此，CsCl型AuZn和PtZn金属间化合物的声子色散曲线会出现明显的带隙. 对于所有的CsCl型结构，横光学波和横声学波在沿着Γ-X、Γ-Z和R-A-Γ方向都是二重简并的. 但四方变形使晶格对称性减小，因此导致TA和TO简并波的劈裂，即沿着Γ-X和R-A-Γ方向劈裂成两部分. 同时，在Γ点还出现了TO/LO分裂，即三重简并模式劈裂为高频纵光学波和低频横光学波. 不过对于c轴 (Γ-Z方向)，由变形导致的振动模式劈裂效应很微弱. 具体表现为，除了在Γ点发生了TO/LO分裂之外，其它横光学波和横声学波仍然保持二重简并. 和CsCl型结构相比，CuTi型结构声学波和光学波之间的频率分化较弱.

计算结果还表明，除了AgZn和AuZn的CuTi型结构(图6 (e) 和 (f))，其它金属间化合物均不存在虚频. 因此，大多数TM-Zn金属间化合物，不论是CsCl型还是CuTi型结构，都具有动态晶格稳定性. 由立方相向四方相变变形仅会导致AgZn和AuZn发生晶格失稳，虚频最小值都出现在R点. 这些结果与基态总能的计算结果一致(图1和2). 此外，虽然CsCl型TM10-Zn不是最稳定的，但声子色散曲线均没有出现虚频. 因此，可以把它们视为特殊的亚稳相.

2.4 电子局域化函数以及TM-Zn化学键

运用VESTA工具软件对电子局域化函数 (ELF) 的拓扑进行可视化分析，深入研究TM-Zn化学键的特点，定量表征原子间相互作用. 因为CsCl型和CuTi型结构的密排面均为 (110) 晶面，故计算了电子局域化函数在(110)晶面的投影，如图8和图9所示.

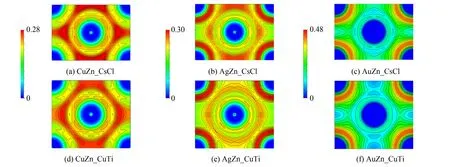
图8 TM11-Zn的CsCl型和CuTi型结构电子局域化函数 (ELF) 在 (110) 面的投影Fig.8 Contour surfaces of electron localization function (ELF) projected on (110) plane of TM11-Zn

图9 TM10-Zn的CsCl型和CuTi型结构电子局域化函数在 (110) 面的投影Fig.9 Contour surfaces of ELF projected on (110) plane of TM10-Zn

电荷主要分布在Zn原子和TM原子的外壳层，或者分散在Zn原子和TM原子之间的间隙里，未出现明显的电荷转移现象. 所以，TM-Zn金属间化合物表现出金属键特征. 而由立方相向四方相变形，使间隙区域的电荷向各原子的外壳层迁移，导致间隙内富电荷区域缩小、 消失，而贫电荷区域扩大、 增加. 此外对于TM10-Zn金属间化合物，分布在TM10外壳层的电荷倾向于偏聚在一起，并形成明显的富电荷核心.

TM-Zn金属键断裂后体系能量的增量，也叫束缚能，束缚能越大，TM-Zn金属键也越强，可用来表征TM-Zn键的强度. CsCl型和CuTi型结构的束缚能如表1所列，不难发现，不论是CsCl型还是CuTi型晶体结构，TM10-Zn金属键的强度都明显高于TM11-Zn的，也就是说，TM10外壳层的电荷偏聚有助于提高其金属键强度. 此外，所有TM-Zn金属间化合物，CsCl型结构束缚能均大于其对应的CuTi型结构束缚能，这表明随c/a比增加，四方变形有削弱金属键强度的趋势.

表1 CsCl型和CuTi型结构TM-Zn金属间化合物的化学键的束缚能

3 结语

1) TM11-Zn和TM10-Zn金属间化合物所对应的稳定结构分别为CsCl型和CuTi型.

2) 在费米能级附近，结构对称性下降所导致的简并轨道劈裂诱发了Jahn-Teller效应，是TM-Zn金属间化合物结构稳定性的原因.

3) 声子色散曲线也证实CsCl型TM10-Zn金属间化合物能够以亚稳态形式存在，而CuTi型AgZn和AuZn金属间化合物是不稳定的.

4) 电子局域化函数及束缚能计算结果表明，TM-Zn金属间化合物主要体现金属键特征.

致谢: 感谢中国科学院金属研究所胡青苗教授和北京航空航天大学孙志梅教授对计算模拟方法上的指导.

[1] AMAR H, JOHNSON K H, WANG K P. Electronic structure of IB-IIB beta-phase alloys[J]. Physical Review, 1966, 148(2): 672-680.

[2] 陶辉锦, 谢佑卿, 彭红建, 等. 贵金属Cu、 Ag、 Au的电子结构和物理性质[J]. 中国有色金属学报, 2006, 16(6): 951-957.

[3] MORII Y, NAGASAWA A, MATSUO Y,etal. Lattice instability in β1-AgZn[J]. J Phys Soc Jpn, 1991, 60(12): 4 160-4 166.

[4] FRIEDRICH M, ORMECI A, GRIN Y,etal. PdZn or ZnPd: Charge transfer and Pd-Pd bonding as the driving force for the tetragonal distortion of the cubic crystal structure[J]. Zeitschrift für Anorganische und Allgemeine Chemie, 2010, 636(9/10): 1 735-1 739.

[5] RODRIGUEZ J A. Interactions in bimetallic bonding: electronic and chemical properties of PdZn surfaces[J]. J Phys Chem, 1994; 98(22): 5 758-5 764.

[6] 汤伟, 朱定一, 关翔锋, 等. 贵金属Au宏观物性的分子动力学模拟计算[J]. 福州大学学报(自然科学版), 2004, 32(3): 321-324.

[7] ISAEVA L, SOUVATZIS P, ERIKSSON O,etal. Lattice dynamics of cubic AuZn from first principles[J]. Phys Rev B, 2014, 89(10). DOI:10.1103/physrevb.89.104101.

[8] ARIKAN N, BAYHAN Ü. First-principles study of electronic and dynamic properties of AgMg and AgZn[J]. Solid State Commun, 2012, 152(10): 891-893.

[9] PEARSON W B. The unit-cell dimensions of “electron phases” formed by b group elements with copper, silver, gold, nickel, palladium and platinum[J]. J Less Common Met, 1986, 120(2): 171-187.

[10] HARRISON N M, DURHAM P J, TEMMERMAN W M. Electrons in partially ordered alloys-Ag0.5Zn0.5[J]. Journal of Physics: Condensed Matter, 1989, 1(21): 3 315-3 324.

[11] SHARMA S K. Structural transformation in thin films of binary alloys[J]. J Mater Sci, 1969, 4(3): 189-194.

[12] SHIMIZU S, MURAKAMI Y, KACHI S. Lattice softening and martensitic transformation in Cu-Ni-Zn β ahase alloys[J]. J Phys Soc Jpn, 1976, 41(1): 79-84.

[13] ORR R L, ROVEL J. Thermodynamics of the structural modifications of AgZn[J]. J Acta Metall, 1962, 10(10): 935-939.

[14] IWASAKI H, FUJIMURA T, ICHIKAWA M,etal. Pressure-induced phase transformation in AgZn[J]. J Phys Chem Solids, 1985, 46(4): 463-468.

[15] OWEN E A, PRESTON G D. The atomic structure of AgMg and AuZn[J]. Philosophical Magazine, 1926, 2(12): 1 266-1 270.

[16] KROMPHOLZ K, WEISS A. X-ray study of the quasibinary system AuZn-PdZn[J]. J Less Common Met, 1976, 50(2): 213-222.

[17] IPSER H, MIKULA A, TERZIEFF P. Lattice parameters and melting behavior of the B2-phase in the ternary gold-cadmium-zinc system[J]. Monatsh Chem, 1983, 114(11): 1 177-1 184.

[18] LIESER K H, RINCK G. Löslichkeit von wasserstoff in legierungen II: das system nickel-zink[J]. Z Elektrochem, 1957, 61(3): 357-359.

[19] NOWOTNY H, BITTNER H. Die Kristallstruktur von PdZn[J]. Monatsh Chem, 1950, 81(5): 679-680.

[20] NOWOTNY H, BAUER E, STEMPFL A. Die Kristallstrukturen von PtZn, PtCd und PdCd[J]. Monatsh Chem, 1950, 81(7): 1164. DOI:10.1007/bf00899370.

[22] CHOUHAN S S, PAGARE G, SANYAL S P,etal. First principles study on structural, electronic and elastic properties of AgX and AuX (X= Mg, Sc, Zn and Cd) intermetallic compounds[J]. Comput Mater Sci, 2012, 65: 58-65.

[23] QI L, CHRZAN D C. Tuning ideal tensile strengths and intrinsic ductility of bcc refractory alloys[J]. Phys Rev Lett, 2014, 112(11): 115 503.

[24] VITOS L. Computational quantum mechanics for materials engineers: the EMTO method and applications[M]. London: Springer-Verlag, 2007:31.

[25] KURTULUS Y, DRONSKOWSKI R. Electronic structure, chemical bonding, and spin polarization in ferromagnetic MnAl[J]. J Solid State Chem, 2003, 176(2): 390-399.

[26] LEE S, HOFFMANN R. Bcc and Fcc transition metals and alloys:a central role for the Jahn-Teller effect in explaining their ideal and distorted structures[J]. J Am Chem Soc, 2002, 124(17): 4 811-4 823.

[27] CHEN W Z, LI Q, JIANG Z Y,etal. Electronic band structure, stability, structural, and elastic properties of IrTi alloys[J]. Physica B, 2012, 40(14): 2 744-2 748.

[28] ASANO S, ISHIDA S. Band Jahn-Teller effect in LaCd[J]. J Phys Soc Jpn, 1985, 54(11): 4 241-4 245.

(责任编辑： 蒋培玉)

The structure stability of TM-Zn intermetallic compounds from first-principles calculations

FANG Yuan, CHEN Zuhua, SA Baisheng, WU Bo

(College of Materials Science and Engineering, Fuzhou University, Fuzhou, Fujian 350116, China)

The induced-condition of Jahn-Teller effect was discussed by analyzing the partial band structure. The phonon dispersion curves were calculated to reveal the lattice dynamic stability and the separation of degenerate vibrational-models during the distortion process. Electron localization functions and bind energies were employed to intuitively describe the binding states of chemical bonds, respectively. The results show that the structure stabilities of TM-Zn(TM=Ni, Pd, Pt, Cu, Ag, Au) intermetallic compounds exist during the tetragonal distortion from cubic phase to tetragonal phase.

transition metal zinc (TM-Zn) intermetallic compounds; phase transition distortion; Jahn-Teller effect; structure stability; first-principles calculations

10.7631/issn.1000-2243.2017.03.0424

1000-2243(2017)03-0424-08

2015-10-23

吴波(1971-)，男，教授，博士，主要从事计算材料学的研究，wubo@fzu.edu.cn

国家自然科学基金资助项目(51171046); 教育部博士点基金(博导类)资助项目(20133514110006); 福建省自然科学基金资助项目(2014J01176); 福建省高等学校新世纪优秀人才支持计划项目(JA10013)

O482.1

A