计及浅水及岸壁效应的KVLCC2船体斜航运动水动力数值计算

郭 燚，罗伟林，刘 凯

(福州大学机械工程及自动化学院，福建 福州 350116)



计及浅水及岸壁效应的KVLCC2船体斜航运动水动力数值计算

郭 燚，罗伟林，刘 凯

(福州大学机械工程及自动化学院，福建 福州 350116)

通过求解不可压缩流动RANS方程, 确定浅水及岸壁效应对船舶水动力的影响. 选用RNGk-ε湍流模型，使用全六面体网格进行离散，数值模拟了KVLCC2船体在不同水深和航道宽度情况下作直航和斜航运动时的粘性流场，得到作用在船体上的水动力. 将计算结果与试验结果对比，验证了计算方法的有效性.

浅水； 岸壁； 船舶操纵运动； 计算流体动力学； 数值模拟

0 引言

现代船舶发展的一个趋势是大型化，然而，我国现有的许多港口和内河航道存在水深不足的情况. 研究表明，当水深吃水比小于3时，将发生浅水效应. 在浅水中运动的船舶，容易产生“下蹲”现象，存在触底的危险. 此外，浅水效应还将带来阻力增加、 船速下降、 舵效变差、 回转性下降、 跑舵等不利影响. 因此，了解船舶在浅水中的运动特性，进行相关的操纵运动水动力分析和计算，对于合理操纵与控制船舶，保证船舶航行的安全性至关重要.

浅水中的船舶操纵运动水动力预报方法包括模型试验、 数据库或经验公式估算、 理论计算和数值计算等. 近年来，基于计算流体动力学(computational fluid dynamics, CFD)技术的数值计算方法获得了快速发展和广泛应用. 该方法主要包括基于势流理论的三维面元法和基于RANS方程求解的粘性流方法. 采用三维面元法，余志兴等[1]对系列60船型及其相当平板求解了在浅水、 浅窄航道中的操纵运动水动力； Yao和Zou[2]预报了系列60船型在浅窄航道航行时的下蹲； Zhou等[3]对KCS船型在浅水、 浅窄航道中的下蹲进行了预报. 与势流方法相比，基于RANS方程求解的粘性流方法近年来获得了更多关注并成为研究热点. 如，Simonsen等[4]自主开发了一类RANS代码对浅水中的KVLCC2船体水动力进行计算，并结合PMM试验对计算方法的有效性进行了验证和确认； Toxopeu[5]应用REFRESCO求解器计算了KVLCC2船模在浅水中作定常斜航运动和回转运动时的粘性流场； 王化明和邹早建[6]基于SSTk-ω湍流模型对浅水中运动的船舶进行了水动力预报； 邹璐[7]应用XCHAP求解器对浅水中运动船舶的水动力进行了预报. 尽管CFD技术在包括无限水域和限制水域的船舶操纵运动水动力计算方面的应用已经取得了丰硕的成果，但该技术的有效性仍需进一步验证和确认[8].

本研究基于RANS方程对计及浅水及岸壁效应的KVLCC2船体运动进行水动力计算. 选用RNGk-ε湍流模型封闭方程，使用全六面体网格进行离散，数值模拟了KVLCC2船体在不同水深、 不同岸壁距离、 不同漂角情况下作低速直航运动和斜航运动时的粘性流场，得到水动力随水深、 离岸距离和漂角的变化规律，通过将计算结果与试验结果[9]对比，验证了计算方法的有效性. 计算中，考虑到傅汝德数小于0.1，忽略了自由面兴波的影响.

1 数学模型

1.1 坐标系

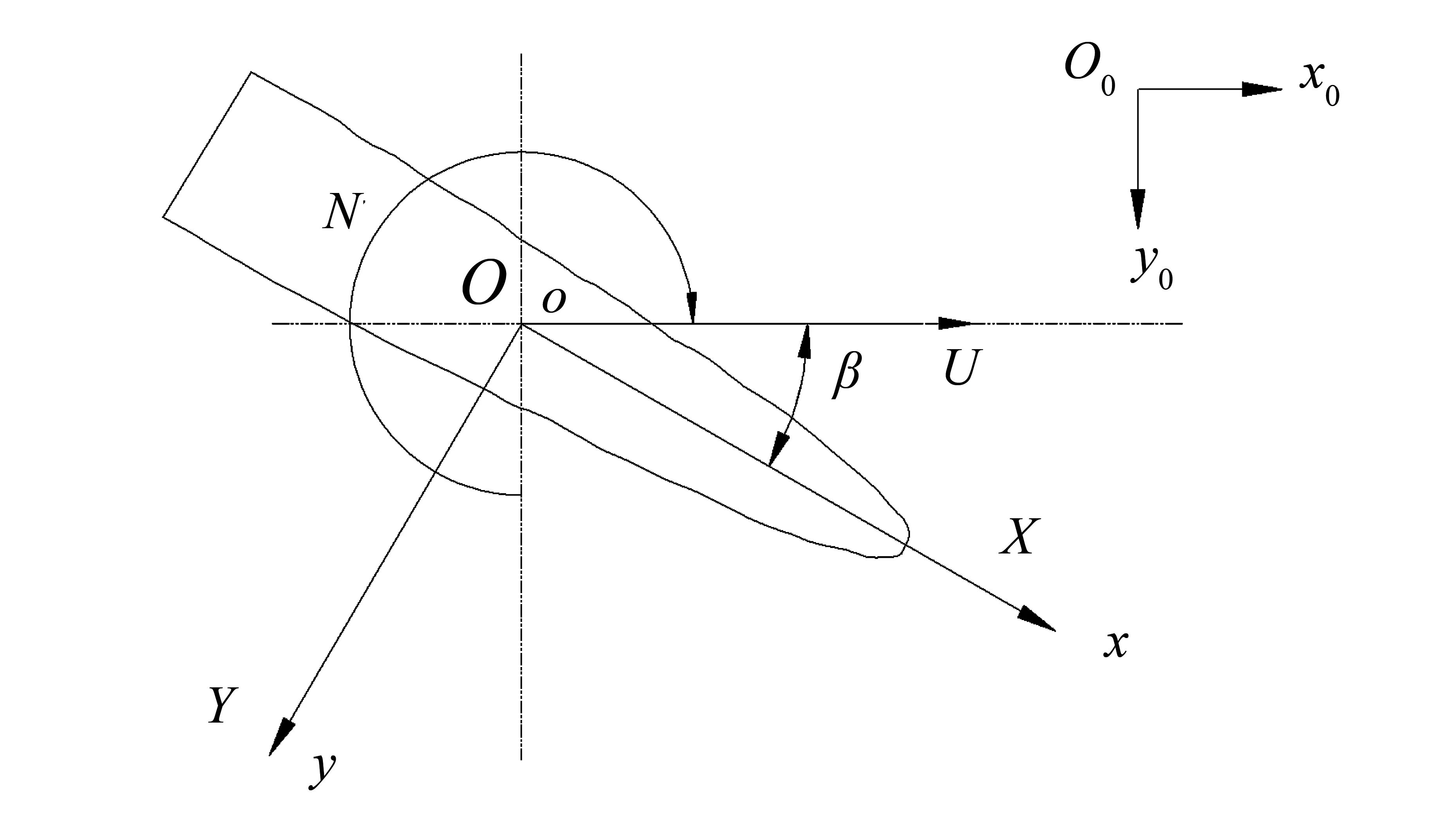
图1 船舶运动坐标系Fig.1 Coordinate system of ship motion

所考虑的物理问题为： 船舶在静水中以定常速度U向前航行，如图1所示，X为纵向力(阻力为-X)，Y为横向力，N为转首力矩，β为漂角； 采用右手直角坐标系： 随船坐标系o-xyz原点位于设计水线面、 中纵剖面、 中横剖面相交处，xoy平面位于无扰自由面上；x轴、y轴和z轴分别以指向船首、 右舷及垂直水面向下为正. 空间固定坐标系为O0-x0y0z0.

1.2 控制方程

在O0-x0y0z0坐标系下，采用雷诺平均方法，控制方程为如下连续性方程和动量方程：

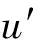
为了封闭方程(1)和(2)，需要建立湍流模型. 综合考虑计算精度和时间[10-11]，选择RNGk-ε两方程模型封闭控制方程，其湍流动能k及湍流动能耗散率ε的方程如下所示：

式中：Gk表示由于平均速度梯度产生的湍流动能； 附加项Rε的表达式为：

相关常数为：η0=4.377，β=0.012，Cμ=0.084 5，C1ε=1.42，C2ε=1.68.

2 计算模型及网格划分

图2 KVLCC 2船型Fig.2 KVLCC2 ship

以KVLCC2船为研究对象，该船是国际拖曳水池会议(ITTC—International towing tank conference)推荐的船舶操纵性研究的基准船型之一，如图2所示. 选择意大利罗马水池INSEAN采用的试验船模，模型缩尺比为1∶45.71，主尺度见表1.

表1 KVLCC2船模主尺度

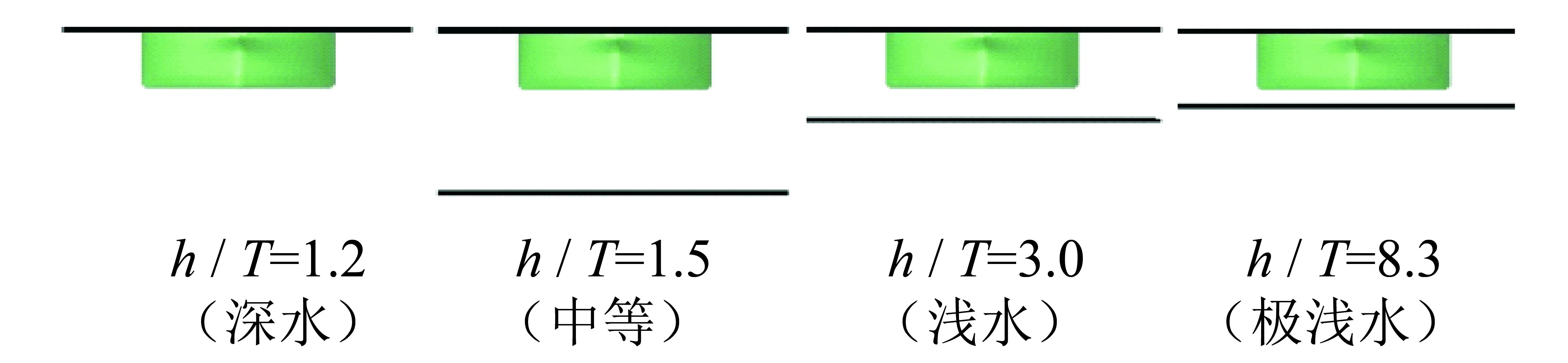
图3 4种不同水深吃水比Fig.3 Different ratio of draught to water depth

数值模拟中，为了与试验工况一致，船模速度取U=0.533 m/s，相应的弗劳德数为Fr=0.064 3，雷诺数为Re=3.7×106. 水深情况用水深吃水比(h/T)来表示，参考文[6]中的工作，在计算中考虑了4种不同水深工况，分别从深水到极浅水的情形，当水深吃水比达到1.5时，认为属于浅水情况，如图3所示.

2.1 计算域及边界条件的设定

选取的计算域如图4所示，水底与船底平行. 根据相对运动原理可假设船舶固定不动，周围流体和水底以速度-U相对船舶运动. 计算域的边界条件设置如下：

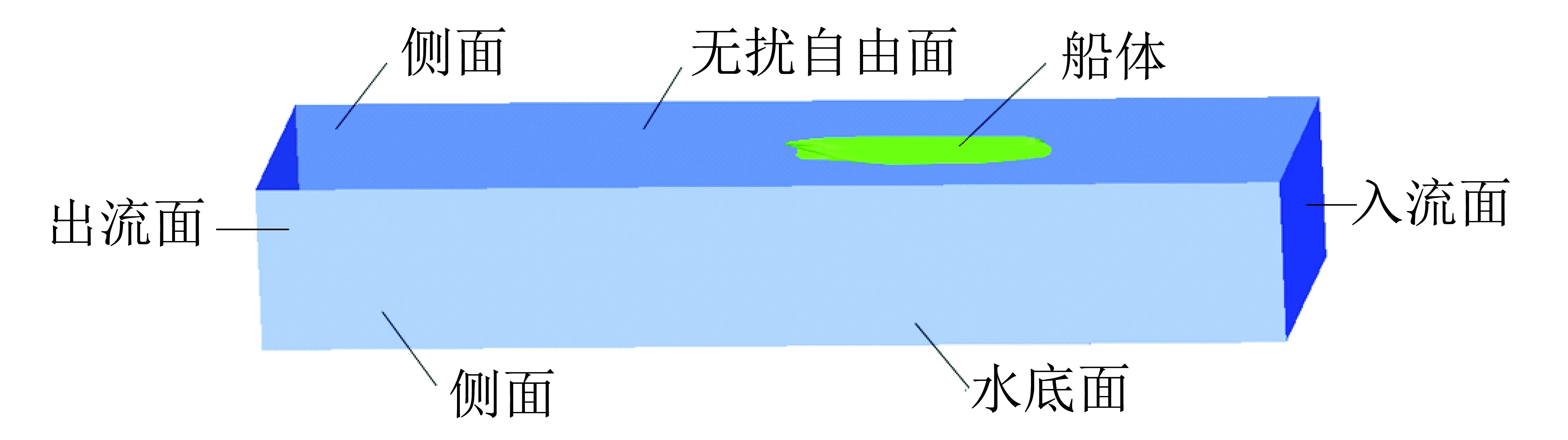
图4 计算域Fig.4 Calculation domain

1) 入流边界. 在船首向前1倍船长的距离处建立入流面，设为速度入口.

2) 出流边界. 在船尾向后2倍船长的距离处建立出流面，设为压力出口.

3) 船体表面. 在船体表面施加无滑移壁面条件.

4) 自由面. 由于船模速度较低(Fr=0.064 3)，自由面兴波的影响可以忽略，因此将其设置为对称面边界，以减少计算量.

5) 其他边界. 为了研究水池岸壁的影响，在数值模拟中考虑了两种宽度的计算域，一种宽度取为1.29 倍船长，该宽度也是进行真实试验时的水池宽度； 另一种宽度取为3倍船长. 岸壁均设为速度入口. 计算域底部平面为水底，其水深根据前述的水深吃水比来确定，水底边界条件设为以速度-U移动的无滑移壁面边界条件.

2.2 网格划分

图5 首部网格Fig.5 Meshes in the bow part

利用前处理软件ICEM进行网格划分，在整个计算域内生成完全结构化六面体网格，图5至图7分别给出了船体首部、 尾部和中横剖面的网格示意图. 在划分网格时采用独特“O”型网格生成技术在船体表面生成六面体边界层网格，通过加密网格保证y+值在30～500范围内. 由于船体首尾部形状比较复杂，故对该部分网格进行了进一步加密，以提高计算精度.

图6 尾部网格Fig.6 Meshes in the stern part

图7 中横剖面网格Fig.7 Meshes in the mid-ship section

3 数值模拟及结果分析

3.1 数值模拟

采用基于RANS方程求解的CFD软件Fluent求解船体周围粘性绕流场，压力速度耦合迭代采用SIMPLE算法，压力项离散采用Standard格式. 动量、 湍流动能和湍流动能耗散率均采用二阶迎风格式，使得到的计算结果有较高的精度. 亚松弛因子取为默认值.

3.2 计算结果及分析

对水动力进行无量纲化：

式中：L为船长(垂线间长).

结合数值模拟结果，水深、 水池岸壁和漂角对船舶水动力的影响分析如下.

3.2.1 水深和水池岸壁对船舶水动力的影响

计算工况包括4种水深、 2种水池宽度得到船舶直航时和漂角β=4°时(目前只能获得漂角β=0°、 4°时的试验数据)的斜航阻力、 横向力和转首力矩，并将计算结果与INSEAN水池提供的试验数据进行对比，对比结果如图8～11所示. 图中横轴代表水深情况，用T/(h-T)表示，与水深吃水比h/T相反，T/(h-T)的值越大表示水深越浅. 为了说明计算结果与试验结果之间的偏差，对试验结果给出了±10%的范围显示.

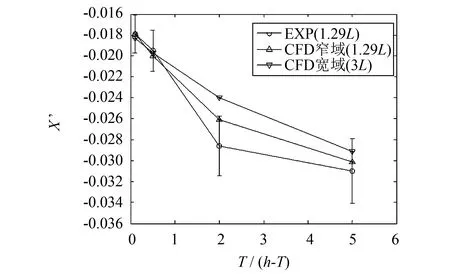
图8 直航(β=0°)时阻力随水深的变化Fig.8 Variation of the resistance with water depth at β=0°

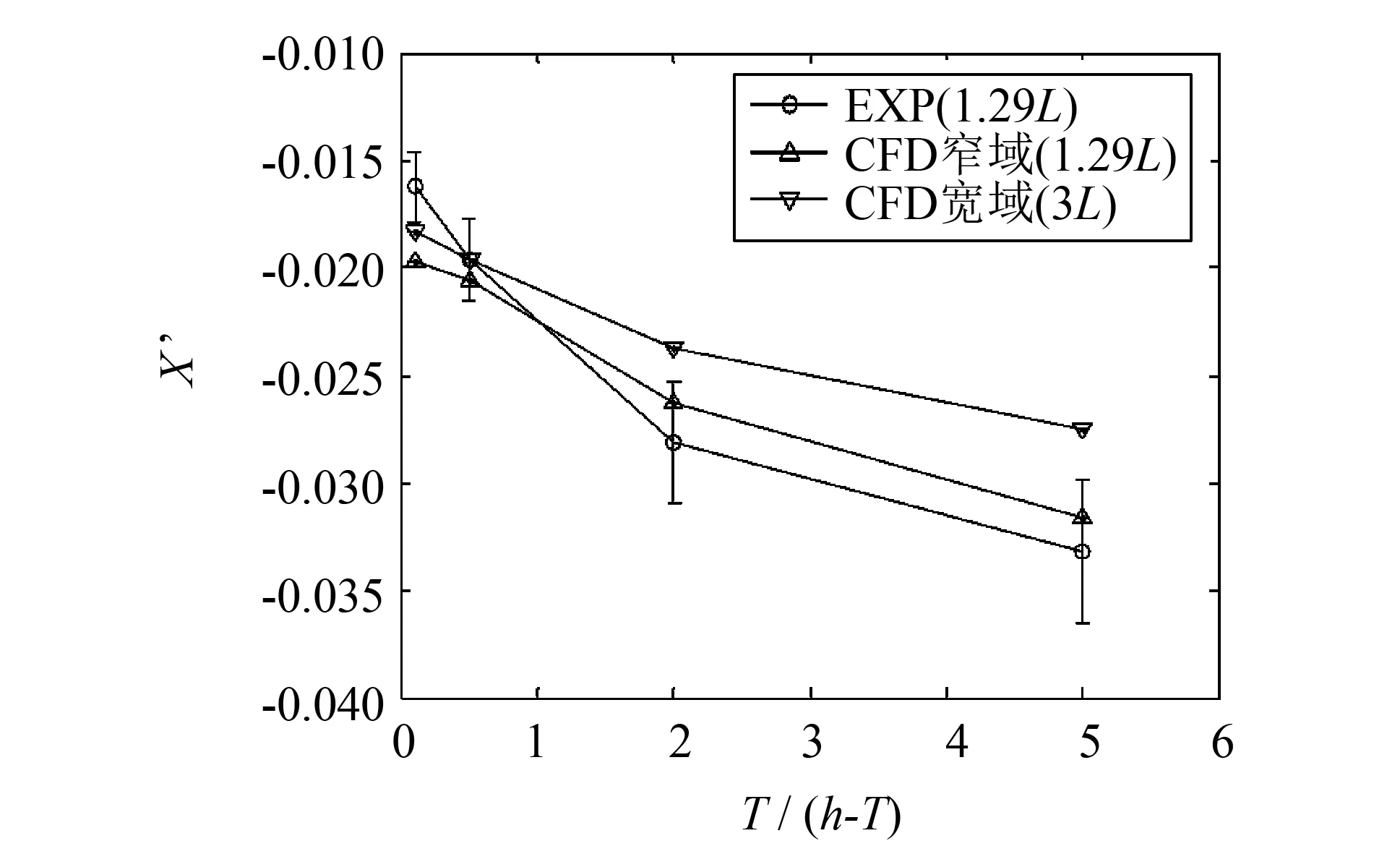
图9 斜航(β=4°)时阻力随水深的变化 Fig.9 Variation of the resistance with water depth at β=4°

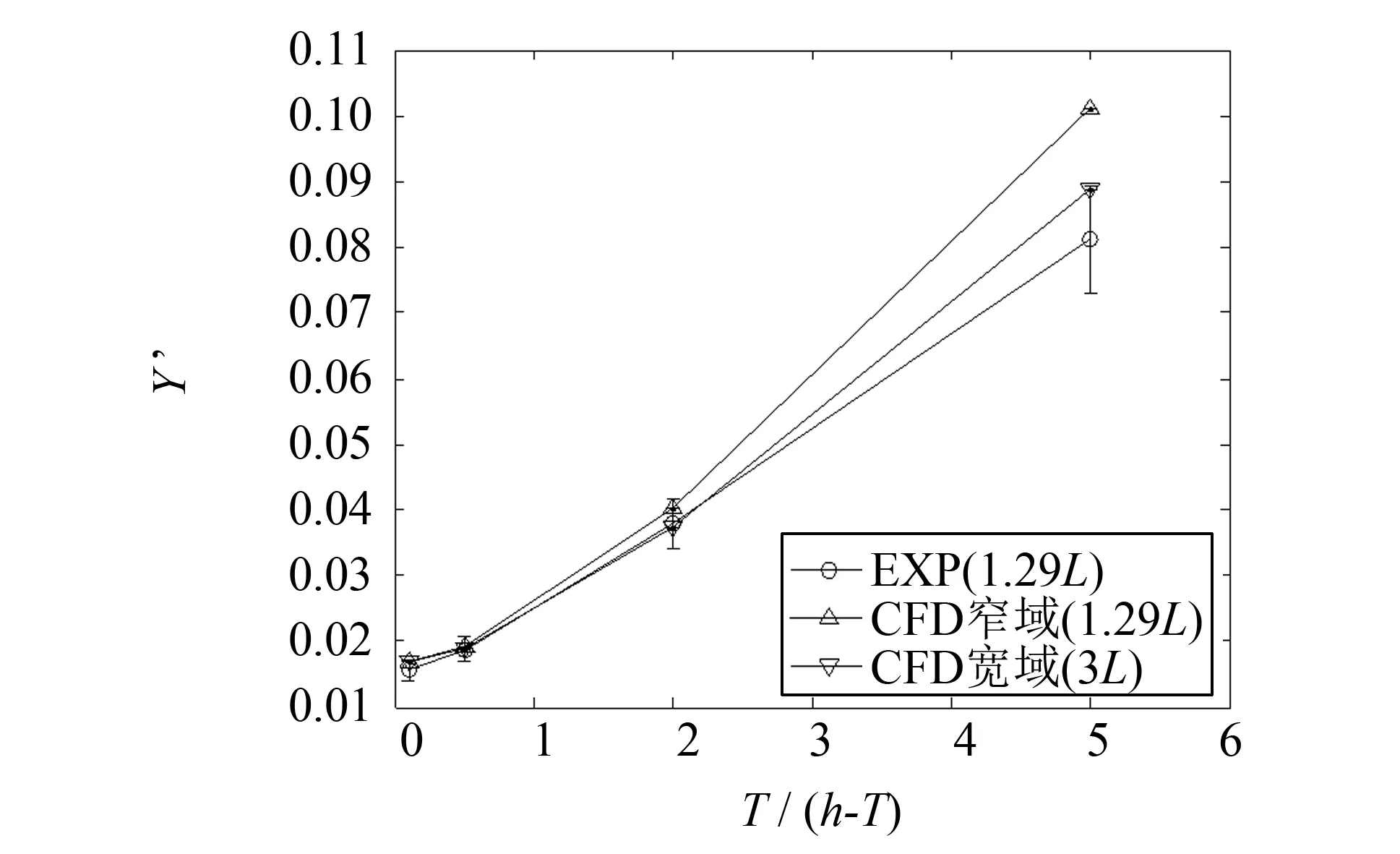
图10 斜航(β=4°)时横向力随水深的变化Fig.10 Variation of the sway force with water depth at β=4°

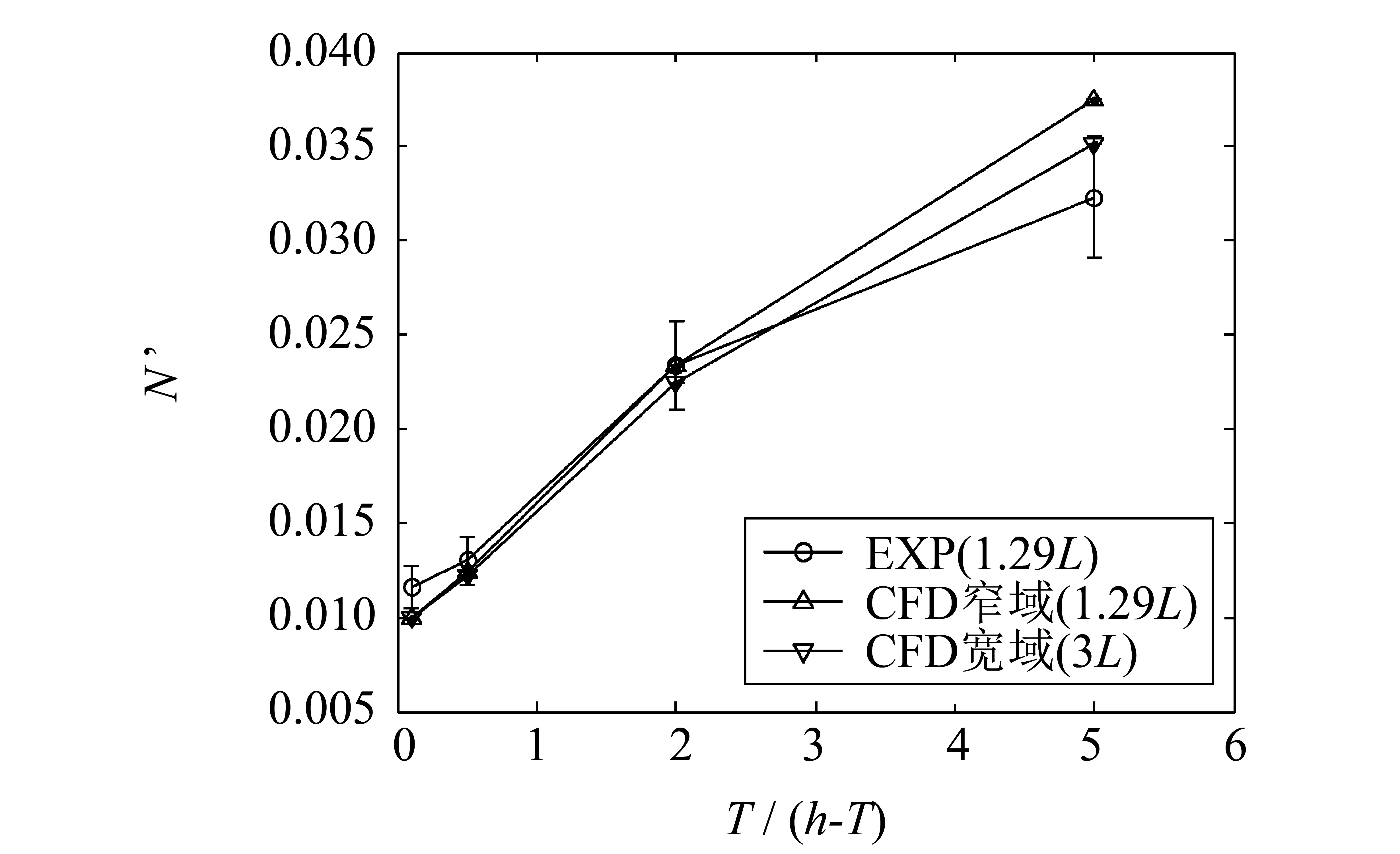
图11 斜航(β=4°)时转首力矩随水深的变化Fig.11 Variation of the yaw moment with water depth at β=4°

从计算结果可以看出，在同样的工况下(即1.29倍船长的水池宽度的情况)，计算结果与试验结果较为吻合. 但对于极浅水情况(T/(h-T)=5)，横向力和转首力矩的计算误差要比其他工况大(由图10和11可见). 究其原因，浅水情况相对深水其水底和船底的间隙更小，绕船体外部的流动也变得更加复杂，因此对网格密度和质量的要求也更高，然而在该情况下生成网格难度要比深水情况大很多(如网格的扭曲率很大)，导致计算结果出现了较大的误差[11].

分析水深对船体水动力的影响，从图中可以看出： 当船舶从深水进入浅水水域时，船舶水动力的变化非常显著，以斜航情况为例(图9～11)，从深水(T/(h-T)=0.1)情况到极浅水情况(T/(h-T)=5)，阻力-X大约增大1.7倍，横向力Y大约增大5.4倍，转首力矩N大约增大3.3倍. 比较而言，从深水情况到中等水深情况(T/(h-T)=0.5)，阻力-X仅增大约1.09倍，横向力Y增大约1.14倍，转首力矩N增大约1.18倍.

表2 岸壁效应随水深的变化

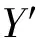
3.2.2 不同水深情况下漂角对船舶水动力的影响

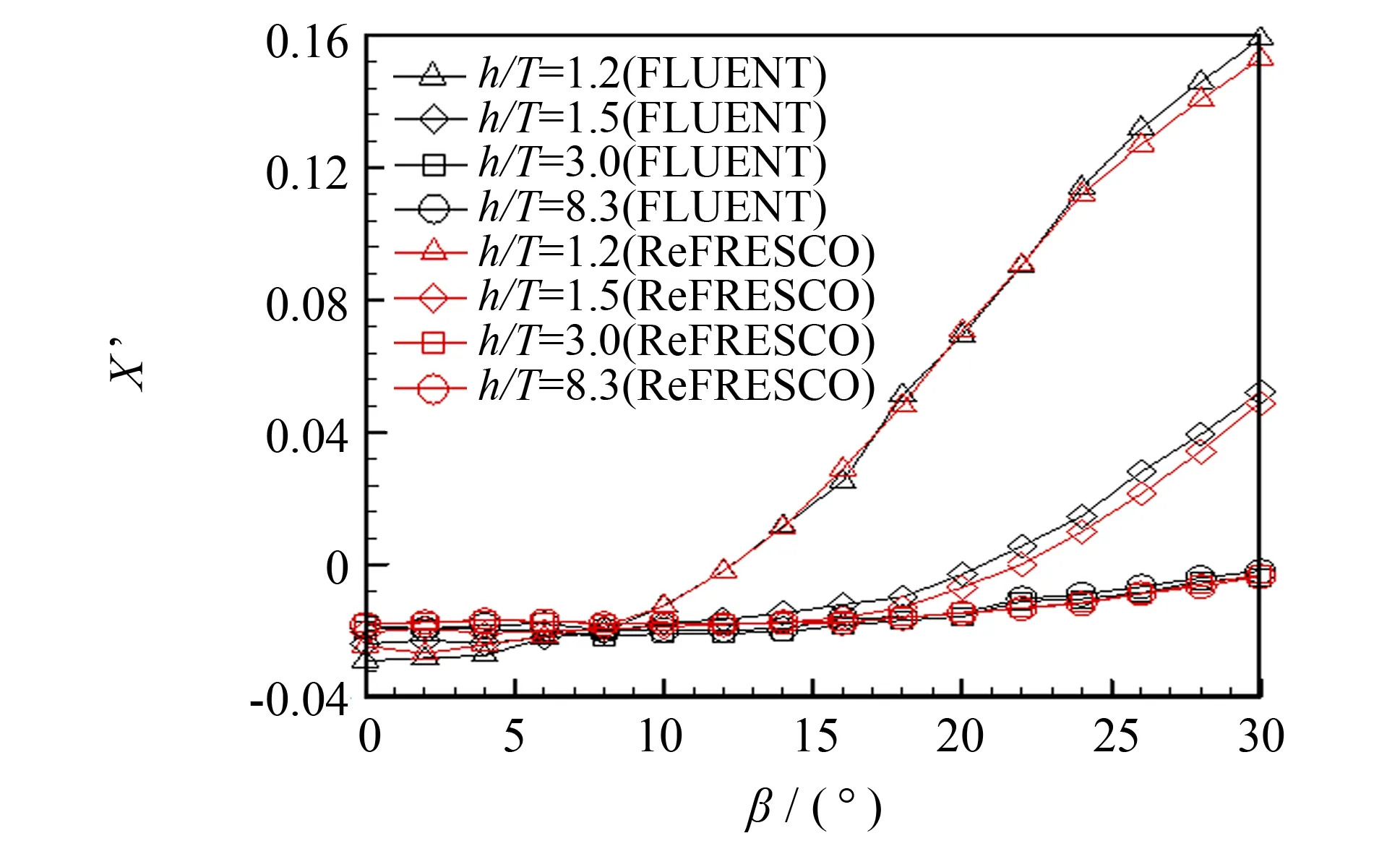
图12 水深和漂角对阻力的影响 Fig.12 Effects of the drift angle and water depth on resistance

研究中，还对不同水深情况下除β=0°、 4°以外的其他漂角情况下的阻力、 横向力和转首力矩进行了数值计算. 图12～14给出了漂角β从0°到30°(间隔2°)变化时不同水深情况下的阻力、 横向力和转首力矩的计算结果及与文[5]中的数值计算结果的比较. 从图中可以看出： 本文计算结果与文[5]给出的计算结果接近； 从水动力变化趋势看，深水情况和中等水深情况下的船舶阻力随漂角的增大而减小，浅水情况下(包括极浅水情况)阻力随漂角的变化则是先减小然后再反向增大； 对横向力和转首力矩，不论水深大小，均随着漂角的增大而增大，对于水深较深的情况，增加幅度较小，而浅水情况下则增加幅度较大.

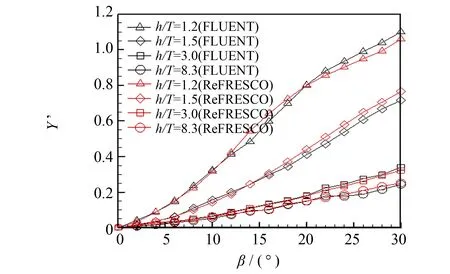
图13 水深和漂角对横向力的影响Fig.13 Effects of the drift angle and water depth on sway force

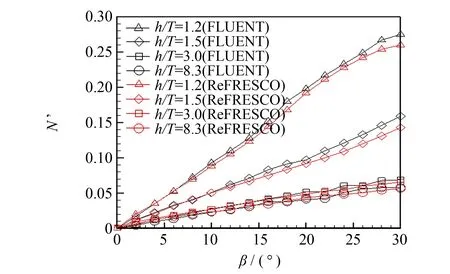
图14 水深和漂角对转首力矩的影响Fig.14 Effects of the drift angle and water depth on yaw moment

4 结语

采用RANS方程求解方法，以KVLCC2船型为对象，对船体在不同水深和不同岸壁距离情况下的低速直航运动和低速斜航运动进行数值模拟，得到船体上所受阻力、 横向力和转首力矩. 通过与试验结果对比，验证了本研究所采用的数值方法能够有效应用于浅水域船舶低速直航和斜航运动时的水动力计算. 计算结果表明，浅水中船舶所受的水动力远大于在深水中所受的水动力，浅水效应明显. 同时，考虑水深和岸壁的影响，则水深越浅，水池岸壁的影响越明显.

针对低速运动的船舶水动力进行了计算. 航速较大时，兴波的影响将不可忽略，下一步的研究将计及自由面兴波的影响.

[1] 余志兴, 吴秀恒, 张乐文. 限制水域中三维船舶操纵运动水动力计算[J]. 武汉交通科技大学学报，1996, 20(6): 677-682.

[2] YAO J X, Zou Z J. Calculation of ship squat in restricted waterways by using a 3-D panel method[C]// Proceedings of the 9th International Conference on Hydrodynamics. Shanghai: Elsevier, 2010，22(5)： 489-494.

[3] ZHOU M G, Zou Z J, Yao J X. Prediction of ship squat in restricted waters[J]. Journal of Ship Mechanics, 2013, 17(6): 625-634.

[4] SIMONSEN C D, STERN F, AGDRUP K. CFD with PMM test validation for manoeuvering VLCC2 tanker in deep and shallow water[C]// Proceedings of the International Conference on Marine Simulation and Ship Manoeuvrability (MARSIM 2006). Tershelling: Transas, 2006: 1-11.

[5] TOXOPEUS S L. Viscous-flow calculations for KVLCC2 in deep and shallow water[C]//Proceedings of IV International Conference on Computational Methods in Marine Engineering (MARINE 2011). Lisbon: Springer, 2013: 151-161.

[6] WANG H M, Zou Z J. Computation of the viscous hydrodynamic forces on a KVLCC2 model moving obliquely in shallow water[J]. Journal of Shanghai Jiaotong University(Science), 2009, 14(2): 241-244.

[7] 邹璐. 浅水中低速斜航运动船舶水动力预报及误差分析[C/OL]//2013年船舶水动力学学术会议. 舟山: 中国造船工程学会, 2013. http://cpfd.cnki.com.cn/Article/CPFDTOTALZGZC201308001065.htm.

[8] STERN F, AGDRUP K, KIM S Y,etal. Experience from SIMMAN 2008： the first workshop on verification and validation of ship maneuvering simulation methods[J]. Journal of Ship Research，2011, 55(2)： 135-147.

[9] FABBRI L, CAMPANA E, SIMONSEN C D. An experimental study of the water depth effects on the KVLCC2 tanker[C/OL]// Proceedings of AVT-189 Specialists' Meeting on Assessment of Stability and Control Prediction Methods for NATO Air and Sea Vehicles. Portsdown West, 2011: 12-14. http://puma.isti.cnr.it/publichtml/section_cnr_insean/cnr_insean_2011-A2-028.html.

[10] 马峥, 黄少锋, 朱德祥. 湍流模型在船舶计算流体力学中的适用性研究[J]. 水动力学研究与进展(A辑), 2009, 24(2): 207-216.

[11] 王化明. 限制水域操纵运动船舶粘性流场及水动力数值研究[D]. 上海: 上海交通大学, 2009.

(责任编辑： 沈芸)

Numerical calculation of hydrodynamic forces on a KVLCC2 hull in the oblique motion with shallow water and bank effects

GUO Yi, LUO Weilin, LIU Kai

(School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou, Fujian 350116, China)

To determine the shallow water and bank effects on ship hydrodynamic forces, numerical simulation of the viscous flow around a KVLCC2 hull in straight forward motion and oblique motion at different water depths and channel widths are conducted. RANS equations are solved. RNGk-εmodel is adopted and hexahedral grids are used. The hydrodynamic forces acting on the hull are obtained. The comparison between the numerical results and experimental results demonstrates the validity of the proposed calculation method.

shallow waters; channel walls; ship manoeuvring motion; computational fluid dynamics; numerical simulation

10.7631/issn.1000-2243.2017.03.0385

1000-2243(2017)03-0385-06

2015-12-18

罗伟林(1973-)，博士，副教授，主要从事船舶操纵与控制研究，wlluo@fzu.edu.cn

福建省教育厅省属高校专项课题基金资助项目(JK2015003)

U661.158

A