改进包络滤波算法及在电路信号中的应用

林德荣，赖添悦，林琼斌，王 武

(福州大学电气工程与自动化学院，福州大学先进控制技术中心, 福建 福州 350116)



改进包络滤波算法及在电路信号中的应用

林德荣，赖添悦，林琼斌，王 武

(福州大学电气工程与自动化学院，福州大学先进控制技术中心, 福建 福州 350116)

分析多次采样取平均值和经典的包络均值方法，指出这两种方法的优缺点. 提出改进的增量包络均值滤波(I-EMF)算法： 先将采样信号递归平均重建，以削弱幅值过高的噪声信号点； 然后在实时提取的重建信号上下包络中引入合理的衰减量； 最后计算包络均值作为真实信号的估计值. 通过仿真分析和实验验证，该算法具有较好的信号处理与去噪性能.

反馈信号； 信号去噪； 包络滤波； 信号检测

0 引言

数字闭环控制系统中的一些高频信号采样电路，反馈信号的采样往往伴随着驱动电路、 振荡器、 电源电路和开关管等相关电磁信号的干扰，这些干扰信号不仅无法避免，还将极大地影响系统后续算法处理的精度和效率. 传统反馈采样信号的处理，大多采用多次采样取平均值或者过采样的滤波方法[1]，这些方法具有一定的去噪能力，减少随机噪声的影响，但运算量较大，占用一定的控制时间，且选择的采样点数多少的不同，滤波效果也会有所差异，存在不稳定的信号失真现象.

经验模态分解(empirical mode decomposition，EMD)方法是一种自适应的数据处理或挖掘方法，适合非线性、 非平稳时间序列的处理，常用于对数据序列或信号的平稳化处理[2]. 文献[3-4]为有效分解噪声信号，基于EMD的基本思路分别提出一些相应的去噪算法； 文献[5-6]充分利用传统EMD的特性，将包络均值滤波(envelope mean filtering，EMF)方法分别应用在图像处理中的图像去噪问题、 心电图QRS波形检测； 文献[7-8]受EMF原理启发，分别提出并行微弱信号检测算法、 基于单自由度振动模型的心脏谱包络提取算法.

结合EMF算法和常用反馈采样信号方法，从数学统计分布规律对信号进行描述和定量分析，提出一种时域信号检测的增量包络均值滤波(incremental envelope mean filtering，I-EMF)算法. 通过仿真验证其对信号去噪的处理性能，将该方法运用到小功率Boost恒流驱动LED电路反馈信号中. 结果表明： 改进的增量包络均值滤波算法具有较好的信号处理与去噪性能，处理后的信号保留原始采样信号的主要波形和变化趋势，具有良好的跟随性.

1 传统反馈信号处理方法

反馈信号采样的过程，一般都参杂着噪声和干扰. 外部干扰可通过一些屏蔽和接地技术加以减弱或者消除[9]. 电路中的噪声，其幅度、 波形、 相位都是随机过程. 设系统采样的混有随机噪声的信号可表示为：

式中:S(t)表示有用信号；N(t)为随机噪声信号；X(t)表示真实采样到的反馈信号，包含原始有用信号和部分噪声信号，是一个幅值多变化、 频率不规则的模拟信号.

1.1 递归均值滤波

传统信号去噪滤波手段如递归平均滤波器，先将每次采样到的新数据放入一个队列数为M的队尾，并扔掉队列的首个数据(采用一种先入先出的窗口滑动原则)，对窗口中的M个数据算术平均运算，获得新的滤波波形[10].

图1 负载切换瞬间电流波形Fig.1 Load switching transient current waveform

式中:f(t)是滤波器的输出，这种滤波器对信号滤波有良好的去噪作用，平滑度高. 但是为达到良好的滤波效果，需要较多采样点数. 一些定点型微控制器运行除法程序，运算量大，占用一定的控制时间，易出现时延现象. 电力电子系统中负载切换瞬间的反馈采样信号如图1所示，处理时由于信号跳变迅速，幅值骤变，多次采样取平均值，其输出的波形必将产生一定的延时，影响系统控制响应.

1.2 包络均值滤波

经典的经验模态分解思路是运用一定的数学方法，将一个频率不规则的波形分解为多个单一频率的波形+残波的形式.

包络线是对采样信号轮廓的描述，不受限于采样信号频率高低，通用性强，依据数据本身的时间尺度特征来进行信号分解.

包络均值算法的包络线是由采样信号的最大值与最小值的连线组成，在这种情况下，一个信号的局部极值点被噪声污染，所得到的平均包络波形局部有所跳变，信号整体变化趋势不明显. 文献[13]针对传统的包络滤波算法，引入一个衰减量δ，通过选取最优衰减量使估计值有效逼近真实信号.

其基本原理示意图如图2所示.

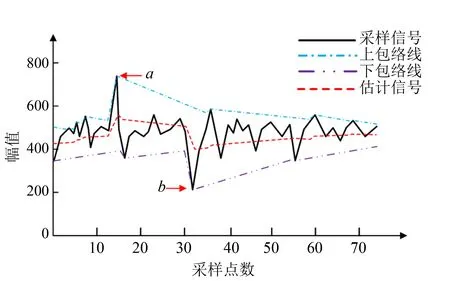
图2 EMF算法波形示意图Fig.2 EMF algorithm waveform diagram

由图2可见，通过添加衰减量，包络线整体信号的波形趋势比较明显，计算出的逼近估计值采样点幅值的波动不是非常剧烈，近似于直流信号的趋势，表现出良好的整体噪声抑制的能力. 但是在反馈信号采样过程中，若噪声干扰严重，遇到如图2中a、b两处信号幅值跳变比较剧烈时，信号的局部估计值跳变也比较明显，得到的平均包络有所扭曲，如图2中a点到b点之间的波形曲线，所体现出来的局部噪声去噪效果不佳. 故必须采取有效措施，在进行包络均值滤波处理之前，削弱或者去除类似图2中a、b两处信号幅值波动比较大的信号.

综合上述两种反馈信号处理方法，递归平均滤波方法整体滤波效果好，平滑度高，但采样点多，易受局部骤变过大的信号影响，有时延缺陷. EMF算法信号滤波效果趋势明显，但容易被局部幅值跳变大的信号影响，使信号出现局部扭曲现象.

2 I-EMF算法理论分析

图3 增量包络均值滤波算法系统模型Fig.3 System mode of the incremental envelope mean filtering algorithm

I-EMF算法系统见图3. 先三次采样递归取平均值将信号平均重建，以削弱幅值过高的噪声信号，由于采样的次数少，对信号的延时性影响小.

再实时提取重建信号上下包络的均值作为真实信号的估计值. 衰减量δ(t)的正确选取对算法的收敛速度影响较大： 衰减量过小时，算法收敛速度缓慢，检测到信号中心所需的迭代次数多，容易出现漏检、 延时现象； 衰减量过大时，算法的收敛速度有明显的提升，但易出现误检现象. 合理的衰减量可以在收敛速度和误检率与漏检率之间达到最佳效果. 针对三次采样信号，合理利用三次采样的相对偏差和偏差量，对衰减量δ(t)的选择做出了以下的设定：

式中：α、β为衰减系数；f(t)的选取为临近三次采样值的平均值；δ(t)的选取与临近三次采样值的偏差及偏差量有关，是一种增量式的计算方法. 式(6)中只有一次除法运算，式(7)中只有加、 减、 乘运算，可以在大部分定点型DSP上实现，计算量小，运算速度较快.α、β值的确定要根据实际的应用进行参数调整. 针对式(4)、 (5)，分析出现的情况有：

1) 若f(t)>H(t-1)-δ(t)，则：

2)若f(t)L(t-1)+δ(t)，则：

3) 若f(t)

3 I-EMF算法仿真与实验分析

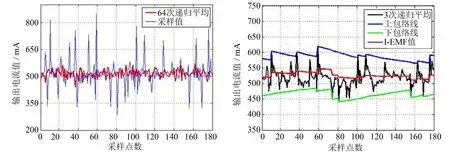
图4 基于F28027的BOOST恒流驱动LED系统Fig.4 BOOST constant current driving LED system based on F28027

为验证上述研究的理论知识在实际工程应用的可行性，搭建一个以12 V的蓄电池为供电电源； TI的32位微处理器TMS320F28027为主要核心控制器； 20个1 W的高亮度LED灯串并联组成负载； 开关频率为20 kHz的简易实验平台，见图4. 实验主要采用0.1 R的高精度采样电阻康铜丝采样输出电流，再搭建相关硬件滤波放大电路.

3.1 静态分析

系统先使用20 Ω的功率电阻作为负载进行静态调试，在PWM输出占空比为0的情况下，硬件相关数据如表1, 运行系统，DSP的12位的AD采样引脚检测到一组数据，通过CCS软件将数据导到Excel文件里，再用Matlab软件生成波形图表，如图5. 反馈采样信号经硬件电路放大，AD量化，由于硬件干扰和噪声影响，出现很多幅值跳变较大的采样点.

表1 占空比为0的硬件检测数据

图5 反馈采样信号Fig.5 Feedback signal sampling

图6为采用递归平均滤波器和I-EMF 算法处理图5数据的效果图. 分析图6(a)可知，在MATLAB仿真软件上，采用递归平均滤波器滤波整体效果明显，波形幅值局部跳变不会非常剧烈. 静态调试中为突出递归平均滤波算法的效果，这里选取采样窗口为64次，为2的6次方，方便微处理器位移运算. 实际应用调试时，考虑动态响应，选取次数可不必这么多. 但是波形在测量值0.52 A上下小范围的来回波动，且有一定的延时，在实际LED调试中，会出现灯光闪烁的现象. 由图6(b)可知，采用I-EMF算法，采样数据先经过三次递归平均，削弱大部分幅值跳变较大的点，再经过增量包络均值滤波，处理后的波形整体趋势明显，幅值的波动不剧烈(极小范围内波动)，近似于直流信号的趋势，表现出良好的噪声毛刺抑制能力.

(a) 递归平均滤波算法 (b) I-EMF算法图6 仿真对比波形图Fig.6 Simulation waveform diagram

3.2 动态分析

系统采用经典的PI算法进行控制，在实际调试过程中，20个1 W的高亮度LED灯串并联组成负载. 改变输出电流的设定值，输出电流从0.8 A跳至1.2 A，再从1.2 A跳回0.8 A. 图7为采用EMF算法和I-EMF算法处理采样的动态数据效果图. 由图7(a)可知，采样信号先经过EMF算法处理，再经PI控制，电流值骤变瞬间输出信号能及时更新运行，但由于部分幅值跳变大的干扰点影响，输出波形不够平稳； 由图7(b)可知，采样信号先经过I-EMF算法处理，再经过PI算法控制，电流值骤变瞬间输出信号能及时更新运行. 由于先经过三次递归采样取平均值，消弱部分幅值偏离较大的干扰点，再合理调试α、β值，输出波形整体效果平稳且光滑.

(a) EMF算法 (b) I-EMF算法图7 实验对比波形图Fig.7 Experimental contrast waveform

4 结语

结合传统一些去噪滤波算法的优点，提出一种新的信号去噪算法-I-EMF算法，通过理论与仿真分析, 该算法的全局收敛性强，对信号的整体和局部信号都有良好的处理效果. 在数字闭环控制系统的反馈采样信号处理中验证该算法的去噪性能，通用性较强. 本算法可作为反馈信号检测的预处理步骤，以提高后续其他算法的稳定性. 下一步将开展算法中衰减系数α、β参数的影响研究，以增强算法的自适应滤波功能.

[1] 蔡逢煌, 江彦伟，王武，等. 单相并网逆变器并网电流的过采样技术[J]. 电力电子技术，2015，49(2): 62-65.

[2] HUANG N E，SHEN Z，LONG S R，etal. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings: Mathematical，Physical & Engineering Sciences，1998，454(1 971): 903-995.

[3] LI L，JI H. Signal feature extraction based on an improved EMD method[J]. Measurement，2009，42(5): 796-803.

[4] PARK M，KIM D，OH H. Quantile-based empirical mode decomposition: an efficient way to decompose noisy signals[J]. IEEE Transactions on Instrumentation & Measurement，2015，64(7): 1 802-1 813.

[5] 张辉，黄永强. 包络滤波算法及其在图像去噪中的应用[J]. 信息技术，2008(2): 1-4.

[7] 刘磊，范铁生，王银斌，等. 基于信号包络分析的并行微弱信号检测算法[J]. 计算机应用，2012，32(8): 2 133-2 136.

[8] CHOI S，CHO S H，PARK C W，etal. A novel cardiac spectral envelope extraction algorithm using a single-degree-of-freedom vibration model[J]. Biomedical Signal Processing & Control，2015，18: 169-173.

[9] 孙士平. 微弱信号检测与应用[M]. 北京： 电子工业出版社，2013.

[10] 黄纯静. 基于FPGA的二维多普勒谱仪数据分析系统设计及实现[D]. 武汉： 华中科技大学，2009.

[11] 李宏伟，刘宇航，杨辉. 经验模式分解改进算法的比较[J]. 东北水利水电，2010，28(4): 53-56.

[12] 滕建方. 基于EMD的时变系统参数辨识[D]. 南京： 南京航空航天大学，2009.

[13] 叶卫东，李行善. 包络均值滤波算法实时检测微弱信号[J]. 北京航空航天大学学报，2010，36(8): 909-912.

(责任编辑： 蒋培玉)

Improved envelope filtering algorithm and its application in the circuit of signal

LIN Derong, LAI Tianyue, LIN Qiongbin, WANG Wu

(College of Electrical Engineering and Automation, Research Center for Advanced Process Control,Fuzhou University, Fuzhou, Fujian 350116, China)

We analyse the multiple sampling average and classic envelope average method, point out the advantages and disadvantages of the two methods. Then an improved incremental envelope mean filter (I-EMF) algorithm is proposed. First, recursiving average reconstruction of sampled signals in order to weaken the noise signal at high amplitude. Reasonable attenuation is then introduced in the real time extraction of the reconstructed signal.Finally, the estimated value of the envelope is estimated as the real signal.Through simulation analysis and experimental verification, the algorithm has better denoising performance and signal processing.

feedback signal; signal denoising; envelope filter; signal detection

10.7631/issn.1000-2243.2017.03.0362

1000-2243(2017)03-0362-05

2016-03-12

王武(1973-)，教授，主要从事电力电子系统分析、 控制算法设计与实现的研究，wangwu@fzu.edu.cn

福建省自然科学基金资助项目(2013J01178)

F407.67

A