基于PEM的三自由度直升机模型辨识*

李亚帅， 邵宗凯

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

基于PEM的三自由度直升机模型辨识*

李亚帅， 邵宗凯

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

针对三自由度(3-DOF)直升机平台的特点，提出了一种基于预测误差法(PEM)的模型频域辨识方法，建立了机理模型，运用扫频技术得到巡航飞行状态直升机3个通道的输入—输出数据；分析了偏相干函数和复合窗函数，通过PEM进行了模型的频域辨识，得到了状态空间方程的待辨识参数和直升机的参数化模型。通过时域飞行和模型预测响应的对比，验证了该模型的准确性和该辨识方法的有效性。

三自由度直升机； 预测误差法； 频域辨识； 状态空间方程

0 引 言

直升机具有垂直升降，空中悬停，低空低速和沿任意方向飞行的性能，因此在诸多领域有广泛应用。三自由度(3-DOF)直升机平台是一个有着双引擎双螺旋桨、多功能的直升机平台，其控制系统是一个复杂的高阶次、非线性、强耦合、开环不稳定和多输入多输出(MIMO)系统，是现代控制理论教学和控制策略方法研究的典型系统[1]。

一般对三自由度直升机的控制研究，在平衡位置对其进行线性化，再利用线性控制方法设计控制器，例如，自适应超螺旋鲁棒控制器[2]，无静差预测控制器[3]，自整定PID控制器等丰硕的研究成果[4]。但是这些研究均在平衡位置有较好的控制性能，脱离该位置后，直升机的鲁棒性能和稳定性能会明显减弱，响应误差增大，运动性能急剧下降。因而，对三自由度直升机平台建立更为精准的模型，为提高其控制性能打下了坚固的基础。系统辨识是控制理论的一个分支，是利用已知先验信息和输入—输出数据建立系统数学模型的科学，其简洁、高效、成本低廉的优点正在逐渐代替传统的建模方法，为已经存在的系统建立模型提供了有效方案[5]。

本文主要研究处于巡航状态下的三自由度直升机平台动力学模型的系统辨识。首先通过机理分析，分别建立高度通道、俯仰通道和旋转通道的参数化模型，根据牛顿—欧拉方程建立状态空间模型；然后进行扫频飞行实验数据采集，通过相干性分析和复合窗分析并运用预测误差方法得到状态空间模型的关键参数的值；最后进行时域验证，通过飞行实验数据和辨识模型输出数据进行对比，可以直观反映出三自由度直升机的运动性能，表明了模型的准确性。

1 三自由度直升机系统模型

三自由度直升机模型如图1所示，其主要由支撑底座、平衡杆、平衡块和2个螺旋桨组成。模型中平衡块和2个螺旋桨分别位于平衡杆的两侧，平衡杆通过万向节接头与支撑底座相连接，螺旋桨旋转产生的升力可以使平衡杆以万向节接头作为支点做俯仰运动，2个螺旋桨产生的速度差可以使平衡杆以万向节为轴做偏航运动。2个螺旋桨作为直升机系统的动力源分别由2个直流无刷电动机进行驱动。通过改变平衡块在平衡杆上的位置来平衡螺旋桨端的提升作用力和重力。

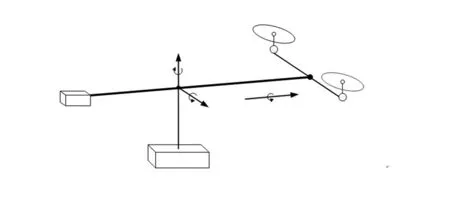
图1 三自由度直升机模型

2 机理模型的建立

根据三自由度直升机系统模型的特点，针对其3个轴(3个自由度)，根据牛顿力学原理建立数学模型[6]。

2.1 高度轴

三自由度直升机的高度由两个机翼的升力Ff和Fb的合力升力Fh和本体重力G决定，当升力Fh大于重力G时，本体上升；反之,本体下降。通过改变2个无刷直流电机的电压vb和vf可以改变升力Fh，即有微分方程等式

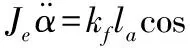
(1)

2.2 俯仰轴

三自由度直升机在横滚轴上所产生的横滚角是由2个螺旋桨产生的升力Ff和Fb之差所决定的，若二者不相等，直升机本体将产生倾斜，升力之差的分力会使直升机围绕支点旋转，因而可得到以下微分等式

(2)

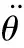
2.3 旋转轴

三自由度直升机旋转角的动力是由螺旋桨在旋转运动时产生的水平分力所提供的。假如2个螺旋桨有升力差，对于微小的角度，2个螺旋桨为直升机提供一个大小为G的合力Fg，就可以在水平方向上产生一个旋转方向的力矩，而使直升机产生旋转加速度。旋转方向的微分等式如

(3)

式中Jt为旋转方向转动惯量；φ为旋转方向的加速度。根据式(1)～式(3)，在较小飞行角度和小干扰的条件下，对三自由度直升机进行简化、线性化得到的状态空间方程为[7]

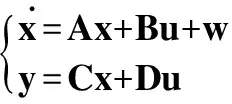
(4)

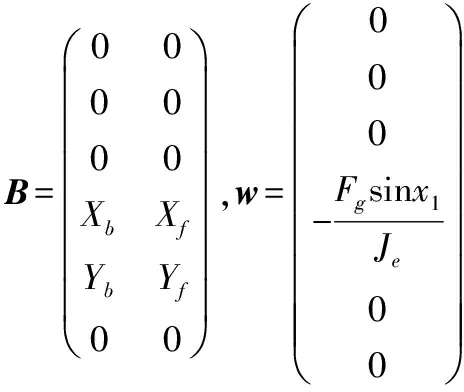
3 频域辨识

针对三自由度直升机的动力学特性，进行频率扫描试验，将获取的输入—输出数据进行复合窗分析，得到优化的频域响应，从而增加频带并降低频谱估计中产生的随机误差。用子空间方法对状态空间模型进行初步辨识，然后采用PEM对该灰箱系统进行辨识得到优化的系统模型。

3.1 相干函数分析

三自由度直升机系统的输入端受噪声影响较小，噪声主要作用于输出端，根据频谱分析法，系统的频率响应可以表示为[8]

(5)

式中H(f)为输入x和输出y之间的频率响应；Gxy(f)为输入x和输出y间的互频谱密度；Gxx(f)为输入x的自频谱密度。相干函数γ是在某个频率为f时，输出频谱由输入频谱所引起的线性相关部分所占的比例的很好地度量，其定义为

(6)

3.2 复合窗函数分析

系统辨识的关键在于得到精准的输入—输出数据，复合窗函数可以降低频谱估计中产生的随机误差，并且可以得到优化的精度较高的频率响应[9]。

对于窗口长度T的选择，关系到模型带宽和随机误差εγ的大小，频域辨识随机误差的表达式为

(7)式中γxy为输入和输出的相干函数;nd=Tγ/T为窗函数的个数，Tγ为辨识时间。由式(7)可以看出，使用大长度的窗口可以降低频谱估计的随机误差，提高精度，但是会导致带宽降低，使包含窗口的信息量减少。为此，本文采用了一种复合窗函数的的方法，其目标函数J(f)为

(8)

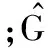
将扫频实验得到的辨识数据，分别经行5，10，15，20，25，30 s的分窗，通过对不同频率采用不同长度的窗函数的复合窗函数的方法可以在较宽范围的频带中经行高精度的频域辨识。

3.3 预测误差方法

PEM作为极大似然估计法的一种推广，是在子空间算法得到一个初始辨识模型的基础上，针对MIMO的状态空间模型，可以得到一个更为精确的辨识模型。PEM不必得到数据概率分布的先验内容，并解决了子空间辨识没有按照最优准则运算造成精度不高以及要保证输入必须不受噪声影响的限制，能够很好地适用于非线性MIMO系统[10]。

子空间辨识方法是利用已知的输入—输出观测序列确定系统状态空间方程的各个矩阵参量和协方差矩阵，具体推算参阅文献[11]。PEM运用时间点k之前的输入输出数据运算出k+1的值，在已知观测量z(k)的基础上，改变η的大小直到得到均方误差最小值。PEM的原理式如式(9)所示

z(k)=f[z(k-1),…,z(1),z(0),u(k-1),…,u(1),η]+e(k)=f[zk-1,uk-1,η]+e(k)

(9)

符合预算条件的z(k)的数学期望即为“最优”预测值，该值满足

(10)

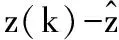
(11)

E=[ε(k)ε(k+1)…ε(k+n)]

(12)

预测误差准则表示为

(13)

模型的状态空间方程和其频率响应矩阵由以下关系方程式表示

T(s)=C(sI-A)-1B+D

(14)

4 扫频实验和辨识结果分析

三自由度直升机平台配备一套数据采集系统，其中包含一个三轴陀螺仪、一个三轴加速度计、一个PCI控制卡和一个飞行控制计算机。如图2所示。

图2 实验使用的三自由度直升机

本文采用扫频技术采集飞行实验所得输入数据，实验在各个通道开环下进行，运用Matlab中的“Chrip”信号输入频率从0.1～5Hz的逐渐增加的激励源。处于巡航状态的直升机扫频实验的部分数据如图3所示。

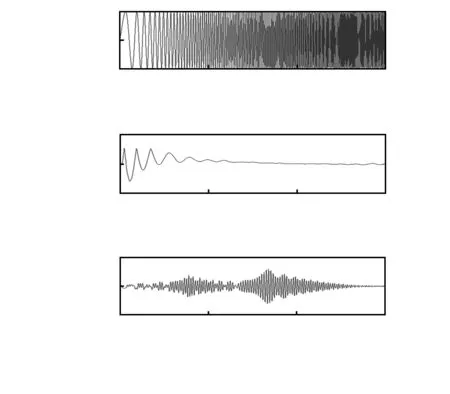
图3 输入和输出扫频数据

高度轴拟合率最高的3个迭代次数分别为5，6，7次，三者对应的拟合率分别为85.43 %，81.26 %，77.01 %，各拟合次数的预测误差部分数据如图4所示。

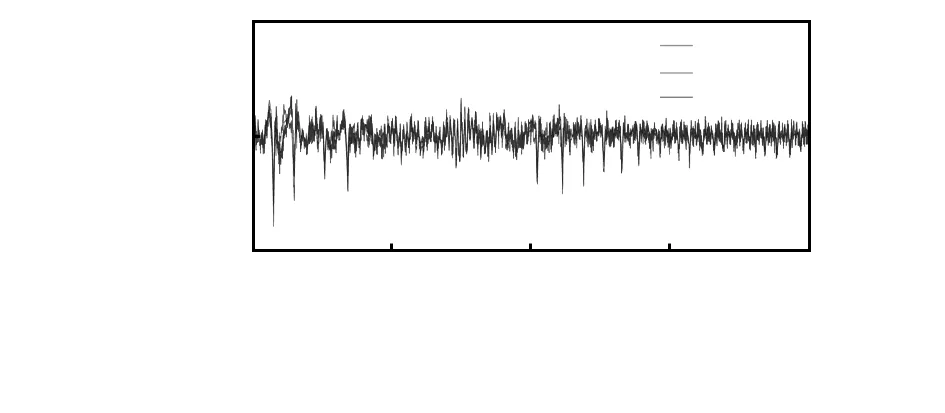
图4 不同迭代次数的误差

图5为实际飞行数据与辨识模型得到的频率响应的参照对比图。从图中可以看出，在高频和低频区域内，相关性相对较差，但是在中频区域，辨识模型和实验数据具有很好地一致性。

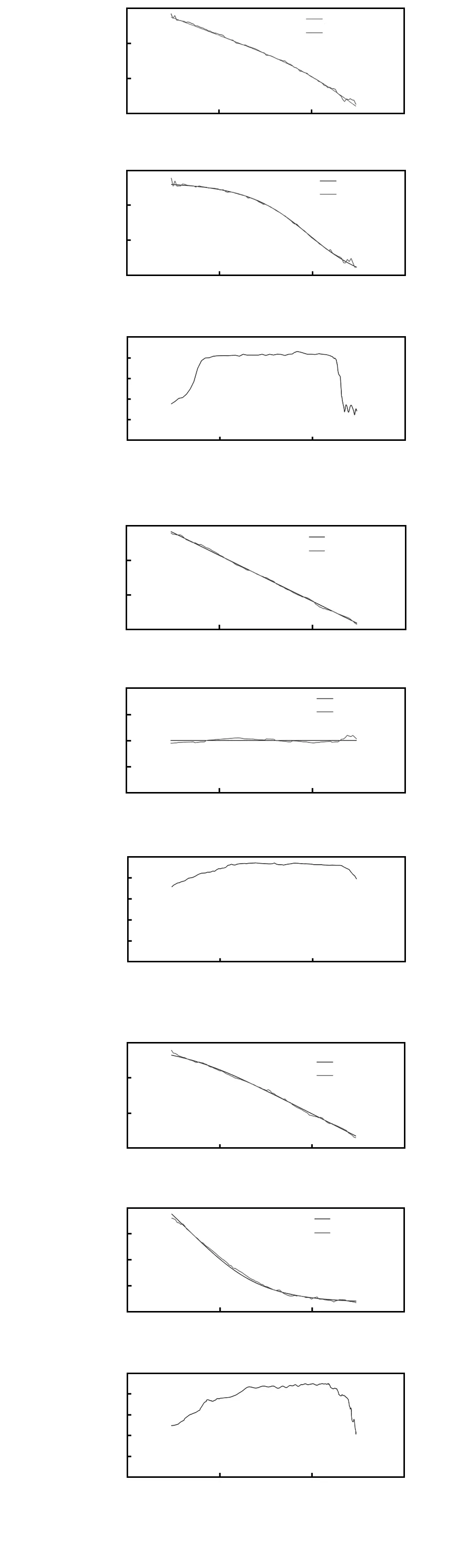
图5 各个通道的频率响应

通过辨识得到的状态空间方程结果为

5 时域飞行验证

时域飞行验证是检验所辨识出的模型的一种有效方法。在确保各个部件和飞行条件没有改变的基础上，重新采集直升机平台的一组输入—输出数据，将该输入数据作为辨识模型的输入值，得到相对应的输出数据，将实际输出数据和辨识模型预测输出数据进行对比[12]。结果通过图6可以看出，曲线走势基本一致，即三个通道的实际飞行输出和辨识模型的预测输出均较为吻合。

图6 实际输出和预测输出比较

6 结 论

本文首先对三自由度直升机平台进行了机理建模，然后通过飞行扫频试验得到巡航状态下的输入—输出数据，对数据进行了相干函数分析和复合窗分析，通过频域预测误差辨识方法得到了状态空间的未知参数。通过时域飞行验证，可以看出飞行输出数据和模型预测数据有很好地一致性，证明了本文辨识模型所运用的方法是有效可行的；对其它模态的三自由度直升机的系统辨识有一定的借鉴作用，为直升机平台飞行控制器的设计奠定了良好的基础。

[1] Liu Hao，Xi Jianxiang，Zhong Yisheng.Robust hierarchical control of a laboratory helicopter[J].Journal of The Franklin Institute，2014，351(1)：259-276.

[2] Plestan Franck，Chriette Abdelhamid.A robust controller based on adaptive super-twisting algorithm for a 3DOF Helicopter[C]∥Proceedings of the IEEE Conference on Decision and Control，Maui， Hawaii，USA，2012：7095-7100.

[3] 纪明达，李德伟，席裕庚.三自由度直升机的无静差预测控制[J].控制工程，2014，21(1):116-119，124.

[4] Boubakir Ahsene，Labiod Salim， Boudjema Fares，et al.Design and experimentation of a self-tuning PID control applied to the 3DOF helicopter[J].Archives of Control Sciences，2013，23(3):311-33.

[5] 刘金琨，沈晓蓉，赵 龙.系统辨识理论及MATLAB仿真[M].北京：电子工业出版社，2013：1-9.

[6] Chabir Alaa，Boukhnifer Moussa，Bouteraa Yassine，et al.Modelling and fixed order robust control of aerial vehicle:Simulation and experimental results[J].The international Journal for Computation and Mathematics in Electronic Engineering，2016，35(3)：1064-1085.

[7] Zhang Ju，Yu Rong.Fast model predictive control of 3-DOF helicopter[C]∥26th Chinese Control and Decision Conference，Changsha，2014：396-3401.

[8] 王 斑，詹 浩，黄 晶.旋转机翼无人机巡航状态飞行力学模型辨识[J].飞行力学，2014，32(2)：179-182,188.

[9] 刘 鹏，武 哲.改进的频域辨识方法及其在直升机建模中的应用[J].控制理论与应用，2011，28(12)：1747-1753.

[10] 李顶根，刘 刚.基于PEM与子空间方法的汽油机空燃比动态模型辨识[J].内燃机学报，2012，30(3)：248-253.

[11] 宋彦国，孙 涛.旋翼飞行器飞行动力学系统辨识建模算法[J].南京航空航天大学学报，2011，43(3)：387-392.

[12] 申 辉，方勇纯，孙秀云，等.基于切换模型的无人直升机偏航通道系统辨识方法[J].模式识别与人工智能，2015，28(2)：148-154.

邵宗凯(1973- )，男，通讯作者，博士，副教授，主要从事智能信息处理、电机智能控制等方向研究工作，E—mail：670416210@qq.com。

Model identification of 3-DOF helicopter based on PEM*

LI Ya-shuai， SHAO Zong-kai

(Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

Aiming at the characteristics of the three degree of freedom(3-DOF)helicopter platform，a frequency domain identification method based on prediction error method(PEM)is proposed.Mechanism model is constructed，and by using frequency sweep flight technique obtain the input and output data of three channels.Partial coherence function analysis and composite window function analysis are carried out in the system.The identification parameters of state-space equation and the parametric model of helicopter are obtained by prediction error method.It can be verified that the model is accurate and effective through comparison of model prediction response and real flight in time domain.

3-DOF helicopter； prediction error method(PEM)； frequency identification； state-space equation

2016—06—16

云南省科技计划资助项目(2015ZC005)

10.13873/J.1000—9787(2017)06—0049—04

V 212.4

A

1000—9787(2017)06—0049—04

李亚帅(1991- )，男，硕士研究生，研究方向为飞行器的建模与控制。