VMD能量熵与核极限学习机在滚动轴承故障诊断中的应用

秦波，王祖达，孙国栋，王建国

（内蒙古科技大学机械工程学院，内蒙古 包头 014010）

VMD能量熵与核极限学习机在滚动轴承故障诊断中的应用

秦波，王祖达，孙国栋，王建国

（内蒙古科技大学机械工程学院，内蒙古 包头 014010）

针对滚动轴承信号的不规则特性，致使信号故障特征难提取及难以辨识，为实现滚动轴承故障的智能诊断，提出基于VMD能量熵与核极限学习机（kernel extreme learning machine，K-ELM）的滚动轴承故障诊断方法。首先将测得振动信号进行变分模态分解（variational mode decomposition，VMD），利用能量熵进一步提取各模态特征组成高维特征向量集；然后将构建的特征向量作为K-ELM算法的输入，通过训练建立K-ELM滚动轴承故障分类模型。实验结果表明：VMD能够很好地分解轴承振动信号，且K-ELM滚动轴承故障分类模型比SVM、ELM故障分类模型具有更高的精度、更强的稳定性。

滚动轴承；变分模态分解；自动编码器；极限学习机

0 引言

滚动轴承是机械设备中最常用的部件，在工作过程中，由于装配不当、润滑不良、水分和异物侵入、腐蚀或过载等都可能使轴承损坏[1]。但是由于加工工艺、工作环境等原因造成其信号非线性、非平稳，而不能有效地检测出故障信号的动力学突变，因此难以精确、稳定地识别轴承的故障类型[2]。

目前，为了高效地对非线性、非平稳性信号进行处理，提出一系列信号处理方法，在特征提取方面有维格纳-威尔分布（wigner-ville distribution，WVD）[3]、小波变换（wavelet transform，WT）[4]、经验模态分解（empirical mode decomposition，EMD）[5]等等。然而它们都存在一定的缺陷，类如模态混叠、端点效应等。文献[6-7]通过VMD与LMD、EMD以及EEMD对比，指出VMD能有效避免模态混叠问题。状态识别方面：文献[8]利用小波分析法和EMD进行信号去噪，小波包分解进行故障特征的提取，BP神经网络进行故障的诊断。文献[9]利用支持向量机进行滚动轴承故障状态的分类识别；虽然上述方法具有一定的有效性，但BP神经网络学习时间较长、易造成欠拟合和陷入局部最优解等缺陷。SVM与BP相比具有更强的稳定性，并能确保局部和全局最优解完全相同。但SVM模型的低稀疏度使其在处理大样本数据时训练时间大幅度增加。Huang[10]提出的极限学习机具有训练时间短、泛化能力强且适合多维度数据训练，但其隐含层节点的输入权值和阈值随机生成，且只有一个隐含层，致使模型的精度低，鲁棒性差。文献[11]使用极限学习机来判别汽轮机的不同故障状态；文献[12]将粒子群算法优化后的极限学习机用于双目视觉摄像机标定，并取得了较好的效果；文献[13]使用遗传算法优化极限学习机，并将其应用于冲击地压危险性预测，得到了有效的预测结果。

针对上述问题，提出基于VMD能量熵与核极限学习机的滚动轴承故障诊断方法。先对测得振动信号进行变分模态分解并提取能量熵组成高维特征向量集；然后将高维特征向量集作为K-ELM算法的输入，通过训练建立K-ELM滚动轴承故障分类模型。

1 相关理论

1.1 变分模态分解

VMD是K.Dragomiretskiy等[14]在2014年提出的一种新的信号时频域分析方法，它的核心思想为变分问题。VMD的分解过程即变分问题的求解过程，包括构造和求解两部分，涉及到3个重要的概念：经典维纳滤波组、希尔伯特变换和频率混合。

1）变分问题的构造

变分问题是将输入信号f（t）分解为n个模态函数Un（t），并对各个模态Un（t）采用Hilbert变换求解得到Un（t）的解析信号，然后与预估中心频率e-jωnt进行混合，在各模态之和等于输入信号f（t）的约束条件下，变分问题如下：

式中：∂t——对t求偏导数；

δ（t）——冲击函数。

2）变分问题的求解

使用拉格朗日乘子γ（t）和二次惩罚因子α对式（1）进行改造，得到增广型的拉格朗日函数：

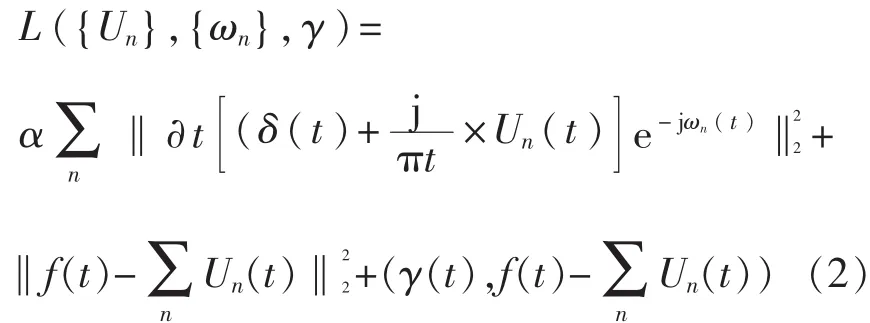
利用交替方向乘子法（ADMM）[15]对式（2）进行迭代求解，迭代次数为k，收敛条件为

然后使用傅里叶等距变换，将迭代后的结果转换到频域上并进行更新，解得：ˆ

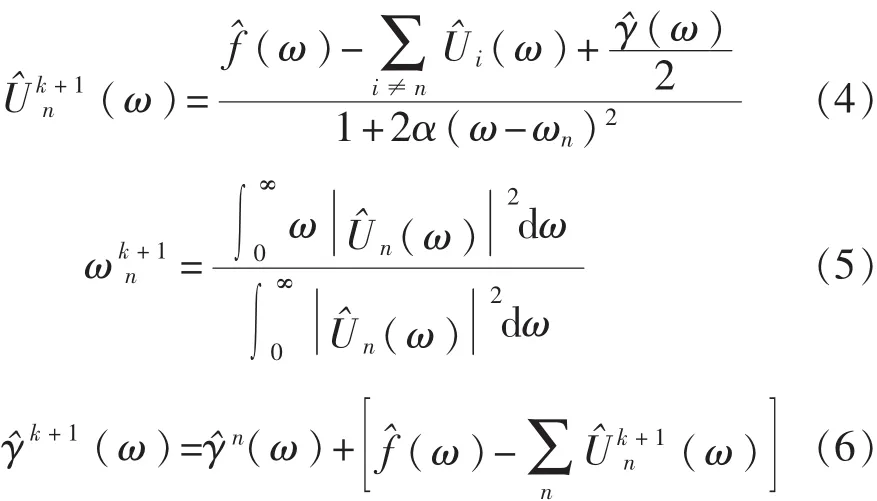
VMD算法步骤：

②根据式（4）～式（6）更新Un、ωn、γ；

③根据收敛条件（式（3））判断结果是否满足，满足则停止计算，否则返回步骤②。

1.2 ELM算法

给定P个不同的数据样本（xj，tj）∈Rn×Rm，对于含有N个隐含层节点，且激活函数为g（x）的单隐含层前馈神经网络（SLFNs）[10]的输出表达式如下：

其中bi为隐含层阈值随机生成，βi是连接输入层和隐含层的权值矩阵，且j=1，2，…，N，若g（x）无限可微，那么就能够零误差逼近输入样本的真实输出值，用公式可以表达为

简写成：

其中H为隐含层输出矩阵：

ELM算法步骤为

1）给定训练样本S={（xj，tj）|xj∈Rn，tj∈Rm，j=1，2，…，N}隐含层激活函数为g（x）；

2）设置隐含层节点数N，算法随机生成输入权重矩阵αi和阈值bi；

3）计算隐含层输出矩阵H；

4）计算输出权重β，β=H*T，H*表示H的Moerr-Penrose广义逆矩阵。

为了提高算法的泛化能力和稳定性，Huang等[10]在β的基础上增加参数1/C公式如下：

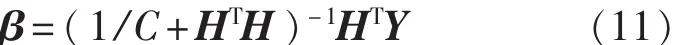
1.3 K-ELM算法

通过引入核函数把低维线性不可分的输入空间样本数据映射到可分的高维特征空间，进行内积运算从而将不可分转变为可分来处理数据。本文采用的高斯核函数满足Mercer核理论[16]，可以作为核函数应用到极限学习机中，其表达式如下：

在ELM的算法中，隐层节点输出函数g（x）是不知道具体形式的函数，那么就可以把g（x）的内积形式用核函数表示出来。所以核ELM算法中，隐层节点输出函数g（x）的具体形式不用给出，只需要知道核函数K（x，xi）的具体形式就可以求出输出函数的值，且隐层节点数能够自适应确定。ELM算法中的公式用核矩阵形式表示为

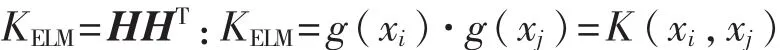
故核函数极限学习机算法可概括为：给定一个含有L个样本的训练样本集（xi，yi），xi表示输入向量，yi表示相应的输出，i=1，2，…，L，及核函数K（x，xi）。则输出的方程为

核极限学习机算法的流程图如图1所示。

图1 核极限学习机算法的流程图

2 实验验证

借助美国Spectra Quest公司轴承动平衡综合模拟试验台（见图2）来验证所提方法的有效性。该实验台由电机、变频器、联轴器与转子等组成。实验采用圆柱滚子轴承，轴承型号为美制ER-10K，其结构参数见表1。加速度传感器分别布置在靠近电机轴承座的水平径向、垂直径向和水平轴向3个方向上采集信号，所采集的振动信号经由LMS Test.Lab数据采集仪（见图3）接入计算机进行分析、保存。滚动轴承的转速为2100 r/min，采样频率为5120Hz，数据的采样点数为5120个。

通过依次对图2中轴承的正常、外圈故障、内圈故障、和滚动体故障4种状态件进行更换，并采集上述4种状态下的振动加速度信号，分别获得每种状态30组数据，每组数据包含5120个采样点。抽取每种状态20组作为训练样本，余下10组作为测试样本。首先对训练样本和测试样本数据进行VMD分解得到其模态U分量，其中，从分解层数为5开始，出现了中心频率相近的模态，本文认为出现了过分解，因此，模态数选为4。如图4内圈故障信号的VMD分解结果，对分解后得到的4个模态分量U1～U4求取能量熵值，可以组成一维特征向量。然后对滚动轴承4种状态的训练样本信号进行VMD分解，求取各模态分量的能量熵值，组成多维特征向量作为K-ELM滚动轴承故障诊断模型的输入。表2为滚动轴承4种状态下测试样本的部分能量熵值。

为验证所提方法的优越性。分别将表1中的特征向量输入到SVM、ELM与K-ELM中进行训练与测试，其中SVM中惩罚参数C与核宽度系数σ设为2与0.2。3种算法的测试样本分类结果分别如图5～图7所示。从图5中看出SVM对于轴承故障分类精度达90%（36/40）；从图6中看出ELM对于轴承故障分类精度达到87.5%（35/40）；从图7中看出，K-ELM对于轴承故障分类精度达到100%（40/40）。上述4种方法的对比结果，如表3所示。

表1 实验轴承结构参数

图2 机械故障综合模拟试验台

图3 LMS Test.Lab数据采集仪

图4 内圈故障信号的VMD分解结果

表2 滚动轴承4种能量熵值

图5 SVM的测试样本分类结果

表3 SVM、ELM、K-ELM 3种诊断模型性能比较

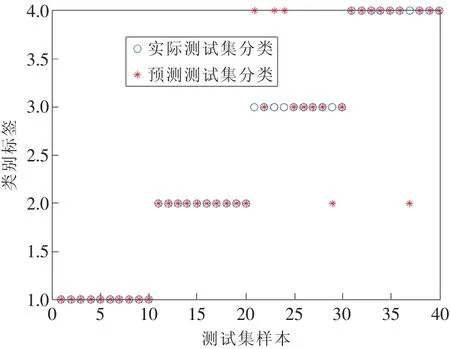
图6 ELM的测试样本分类结果

图7 K-ELM的测试样本分类结果

3 结束语

针对滚动轴承振动信号的不规则性和复杂性，导致轴承状态难以有效识别的问题，提出基于核极限学习机的滚动轴承故障诊断方法。VMD作为一种新的方法用来分解振动信号得到模态分量，本质是一组白适应维纳滤波器，各模态携带着不同频率的滚动轴承故障信息，对其提取能量熵值能够更精确地表达故障特征。然后利用提取的各模态分量的能量熵作为本模型的输入，进行轴承故障的分类和识别。通过实验结果分析，得出所用方法对比SVM、ELM具有良好的效果以及更高的模型的精度与鲁棒性，在轴承故障诊断领域有广泛的应用前景。

[1]ZHANG X Y，LIANG Y T，ZHOU J Z，et al.A novel bearing fault diagnosis model integrated permutationentropy，ensemble empirical mode decomposition andoptimized SVM[J].Measurement，2015（69）：164-179.

[2]郑近德，程军圣，杨宇，等.多尺度排列熵及其在滚动轴承故障诊断中的应用[J].中国机械工程，2013，24（19）：2641-2646.

[3]黄海波，李人宪，丁渭平，等.基于EMD-WVD的车辆悬架减振器异响声品质客观评价研究[J].振动与冲击，2015，34（18）：154-160.

[4]王宏超，陈进，董广明，等.可调品质因子小波变换在转子早期碰摩故障诊断中应用[J].振动与冲击，2014，33（10）：77-80.

[5]马文朋，张俊红，马梁，等.改进的经验模式分解在机械故障诊断中的应用[J].振动、测试与诊断，2015，35（4）：637-644.

[6]武英杰，甄成刚，刘长良.变分模态分解在风电机组故障诊断中的应用[J].机械传动，2015（10）：129-132.

[7]WANG Y X，MARKERT R，XIANG JW，et al.Research on variational mode decomposition and its application in detecting rub-impact fault ofthe otor system[J]. Mechanical Systems and Signal Processing，2015（60-61）：243-251.

[8]王斌.基于小波分析和BP神经网络的滚动轴承故障诊断方法研究[D].兰州：兰州交通大学，2014.

[9]向丹，岑健.基于EMD熵特征融合的滚动轴承故障诊断方法[J].航空动力学报，2015，30（5）：1149-1155.

[10]HUANG G B，ZHU Q Y，SIEW C K.Extreme learning machineaheory and applications[J].Neurocom-puling，2006（70）：489-501.

[11]陈立军，孙凯，侯媛媛.基于极限学习机的汽轮机故障诊断[J].化工自动化及仪表，2013，40（4）：435-438.

[12]周东凯，李刚，王学馄.基于PSO-ELM的双目视觉摄像机标定[J].广西大学学报（自然科学版），2014，39（6）：1285-1290.

[13]朱志洁，张宏伟.基于GA-ELM的冲击地压危险性预测研究[J].中国安全生产科学技术，2014，10（8）：46-51.

[14]DRAGOMIRETSKIY K，ZOSSO D.Variational mode decomposition[J].IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[15]LIU H，SONG B，QIN H.An adaptive-ADMM algorithm with supportand signal value detection for compressed sensing[J].IEEE Signal Processing Letters，2013，20（4）：315-318.

[16]WIDROW B，GREENBLATT A，KIM Y，et al.The No-Prop algorithm：a new learning algorithm for multilayer neural networks[J].Neural Networks，2013（37）：182-188.

（编辑：刘杨）

App lication of VMD and hierarchical extreme learning machine in rolling bearing fault diagnosis

QIN Bo，WANG Zuda，SUN Guodong，WANG Jianguo
（School of Mechanical Engineering，Inner Mongolia University of Science&Technology，Baotou 014010，China）

According to the irregularity characteristics of the rolling bearing signals causing the bearing condition identified difficultly，the kernel extreme learning machine fault diagnosis model is proposed.Firstly，the measured vibration signals are decomposed into variational mode decomposition，using the energy entropy to extract the features of each model to form a high dimensional feature vector set.Secondly，the combined feature vector is used as the input of the algorithm，and the fault classification model of the rolling bearing of the hierarchical limit learning machine is established.The experimental results show that the K-ELM rolling bearing fault classification model is better than ELM，and the SVM fault classification model has higher accuracy and stronger stability.

rolling bearing；variational mode decomposition；automatic encoder；extreme learning machine

A

1674-5124（2017）05-0091-05

10.11857/j.issn.1674-5124.2017.05.019

2016-08-03；

2016-09-19

国家自然科学基金（51565046）；内蒙古自然科学基金（2017MS0509）；内蒙古科技大学创新基金（2015QDL12）

秦波（1980-），男，河南南阳市人，讲师，硕士，研究方向为复杂工业过程建筑、优化及故障诊断。