太赫兹时域光谱测量液体光学常数的不确定度分析
2017-06-08张放杨霏
张放,杨霏
(1.贵阳职业技术学院生化工程系,贵州 贵阳 550023;2.贵州省计量测试院,贵州 贵阳 550003)
太赫兹时域光谱测量液体光学常数的不确定度分析
张放1,杨霏2
(1.贵阳职业技术学院生化工程系,贵州 贵阳 550023;2.贵州省计量测试院,贵州 贵阳 550003)
为建立太赫兹时域光谱测量液体样品光学常数的不确定度分析模型,针对以比色皿为样品池的太赫兹透射式测量系统,推导其测量方程。确认太赫兹幅值测量、样品厚度、比色皿厚度、比色皿倾角及近似传递函数等误差来源,以及这些误差在测量过程中的传递模型,得到表示它们各自不确定度与合成不确定度关系的解析公式。实验测量邻苯二甲酸二辛酯(DEHP)的折射率和吸收系数,并计算它们各自的测量不确定度的量级分别为0.01和1 cm-1,结果表明该不确定度评定模型可以成为评估光学常数测量结果准确性的基础。
太赫兹;光谱学;测量不确定度;比色皿;光学常数;误差传递
0 引言
太赫兹时域光谱技术(THz-TDS)是物质识别的重要工具[1]。到目前为止,利用太赫兹时域光谱技术的物质识别和成分分析的报道井喷式地增加,如爆炸物[2]、半导体[3]、水[4]、生物组织[5]等样品都可以通过太赫兹时域光谱技术检测。但是,由于各个实验室的太赫兹系统的差异性,测量得到的光谱数据相应的存在差异,甚至出现不同实验室对同一物质测得的光学常数相差较大的情况,如文献[6]和文献[7]分别测得水在0.5THz的折射率在2.3和2.05左右。因此,如何在相同标准下评价测量结果的准确性,即测量不确定度的评定问题,已经成为了太赫兹时域光谱测量技术研究需要迫切解决的问题[8]。到目前为止许多关于太赫兹时域光谱测量固体样品的噪声和不确定度分析的研究。从HüBers等[9]和Hiromoto等[10]研究部分测量误差来源到Duvillaret等[11]和Withayachumnankul[12-13]提出一种太赫兹时域光谱技术测量固体样品的不确定度分析模型。但是,相对于固体样品,由于液体样品的测量过程需要考虑液体样品载体(如比色皿)对于测量准确度的影响,它的参数提取过程和相应的测量模型是完全不同的。因此有必要考虑液体类样品太赫兹光谱测量的误差来源及不确定度分析。已有报道研究了基于反射式太赫兹时域谱的光学参数测量与误差分析(垂直反射式[14]和衰减全反射式[15]),本文将分析透射式太赫兹光谱测量液体样品的随机和系统性误差的来源,并建立测量结果的不确定度分析模型,以便各个实验室能够在相同标准下评价测量结果的准确性。
1 基于透射式太赫兹光谱技术液体样品测量函数
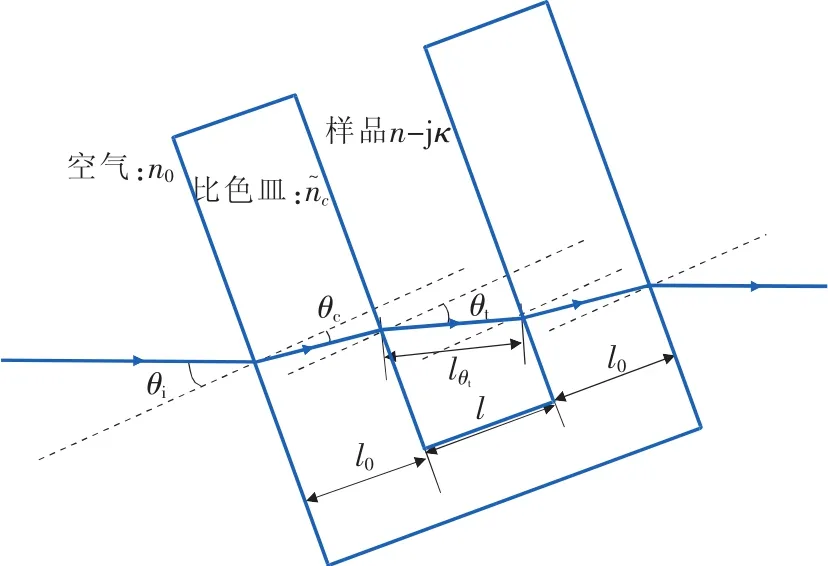
如图1所示,对液体的测量常常选用比色皿作为样品池。实验过程中测量得到3个太赫兹信号的频谱——通过空气的太赫兹频谱Eair(ω),通过空比色皿的太赫兹频谱Ec(ω),以及通过比色皿中样品的太赫兹频谱Esam(ω)[17]:
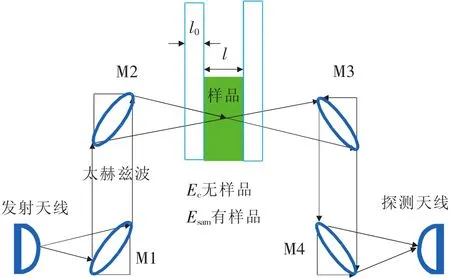
图1 透射式太赫兹时域光谱系统的太赫兹传播路径图[16]
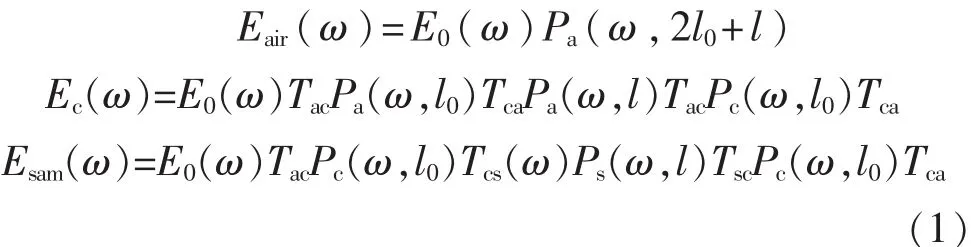
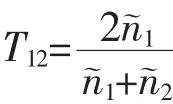
以Esam(ω)为样品信号,Ec(ω)为参考信号的传递系数函数H1(ω)计算得到:
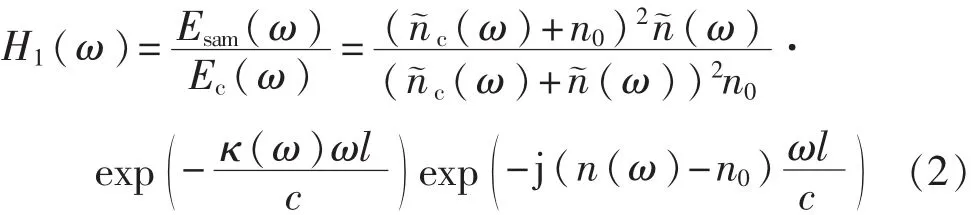
以Ec(ω)为样品信号,Eair(ω)为参考信号的传递系数函数H0(ω)计算得到:

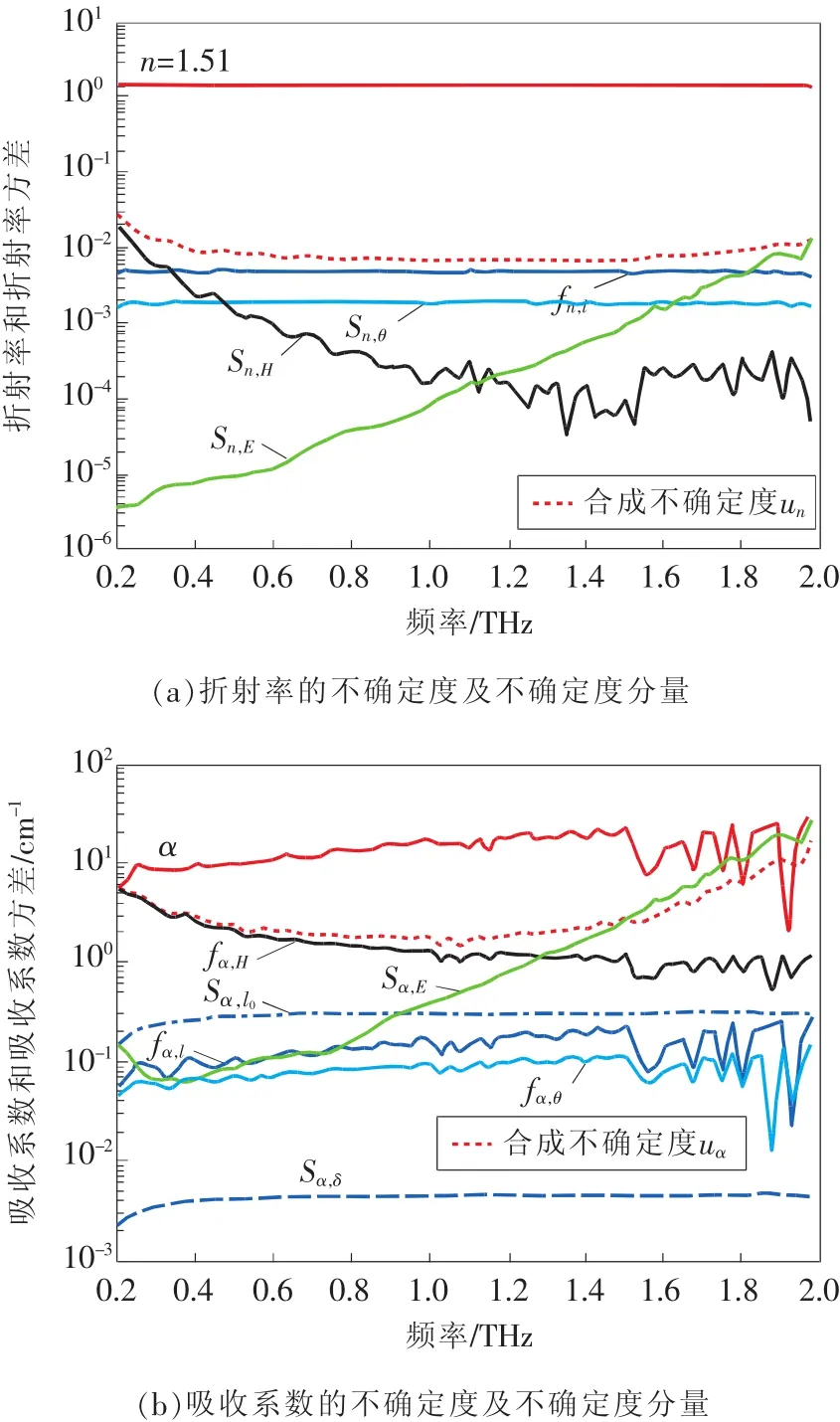
在弱吸收的近似下,即κ< 利用3个太赫兹频谱可以计算得到液体样品的折射率n(ω)和吸收系数α(ω)。 其中nc表示太赫兹波通过比色皿的折射系数,它可以通过下面的式子计算: 光学常数可以通过式(6)~式(8)在太赫兹时域光谱测量过程中得到,这3个方程被称为测量函数。 在THz-TDs测量和参数提取过程中会有很多的误差来源,其中比较重要的误差来源以及在参数提取的过程的误差传递模型如图2所示。虚线框里的误差源在THz-TDS测量和参数提取过程中都会发生。这些来源产生的误差分为系统和随机误差,它们引入的方差和偏差沿图标所示向下传播,最终构成光学常数不确定度的分量。 图2 太赫兹时域光谱测量的误差来源及传递路径 在时域信号测量时幅值误差在参数提取过程中通过傅里叶变换和反卷积传递到传递函数的幅值和相位误差。在计算样品光学参数的过程中,样品厚度、比色皿倾斜角都是不确定度的误差来源。此外传递函数模型的近似处理是一个系统误差。所有这些误差分量构成了最终光学参数的测量不确定度。 接下来将详细分析主要的误差来源及其与光学常数测量不确定度的关系,最后在此基础上得到光学常数的合成不确定度。 2.1 太赫兹时域信号幅值误差 假定3个太赫兹信号的频谱——通过空气的太赫兹频谱Eair(ω),通过空比色皿的太赫兹频谱Ec(ω),以及通过比色皿中样品信号的太赫兹频谱Esam(ω)所对应的幅值方差分别是(k),(k)和(k),那么结合文献[12],经过复杂的推导过程,可以得到光学常数中幅值相关的方差为 其中 式中:Im2、Re2——复数的虚部和实部的平方; τ——太赫兹信号两个取样点的间隔; kτ——第k个取样点的取样时间。 式(9)表明,增加样品厚度会减小光学常数的不确定度。这背后的物理意义是厚的样品可以使得太赫兹波与其充分相互作用,得到的样品信号更加准确。但是由于|Esam|∝exp(-l),增大样品厚度会降低信号幅值从而增大总的不确定度。 2.2 样品厚度的随机误差与系统误差 影响样品光学常数测量结果的一个重要参数就是太赫兹波在样品中的传播距离。当正入射时,传播距离就等于样品的厚度。一般来说,比色皿光程(即样品厚度)的标称值l的公差pl是已知的,其引出的误差是随机误差。该误差造成的光学常数不确定分量为 比色皿的壁厚l0是通过测量得到的,因此l0测量误差就包括随即误差和系统误差。假设测量l0的随机误差的方差为s2l0,根据式(6)、式(7)可以推导出厚度误差导致的样品光学常数的方差为 相对于随机误差,由于测量仪器的分辨率导致的误差被认为是系统误差。一个测量设备的分辨率是有限的,导致的测量误差是系统误差。假设测量设备的分辨率是δl,则分辨率极限引起的样品厚度方差是δl2/12,与随机误差的推导类似,因为误差传递函数相同,所以分辨率极限的标准不确定分量为 从式(11)~式(14)可以看出样品越厚,比色皿厚度越大,其引出的光学常数不确定度分量就越小。 2.3 样品倾斜角度的随机误差与系统误差 当放置比色皿时,很小的倾角都会导致太赫兹波在样品的路径变长,如图3所示。这种误差的类型根据实际的实验过程确定。如果在实验过程中每次测量要重新放置样品池,该误差是随机的。相反如果在实验过程中样品池固定,则视为系统误差。在下面的分析中将假设倾角偏差的最大范围包含两种情况。 图3 倾斜的比色皿中太赫兹波传播路径 根据图3,折射角θt与入射角θi有关,根据Snell定律,n sinθt=n0sinθi,当倾斜很小时,θt≈θi。太赫兹波在样品中实际传播距离的lθ和比色皿中传播的距离l0,θ是倾斜角θi的函数,即: 假设折射角在很小的范围[-fθ,fθ]内变化并且其算术平均值为0,则该倾角导致的传播距离最大偏差为 则根据式(6)、式(7),fl导致的光学常数的偏差可以计算得到: 式(19)、式(20)表明比色皿倾角误差对折射系数的影响与样品厚度无关,而样品越厚会部分减小吸收系数的偏差。并且倾角越大,光学常数的不确定度越大。 2.4 近似传递函数的系统误差 测量函数是基于弱近似假设下将传递函数近似得到的,这样就会导致测量结果存在系统误差。该系统误差可以在不考虑近似的情况下通过数值算法移除,但是这种算法往往需要复杂的迭代计算。研究者们往往会综合考虑算法耗时和近似误差的大小来确定是否采取近似处理。这就需要对近似传递函数的系统误差进行评估。通过计算可以得到,近似处理造成的传递函数的相位偏差和幅值误差为 根据测量函数,相位偏差导致的折射系数的偏差和吸收系数的偏差分别为 同样地,可以计算: 因此 式(25)、式(26)表明样品越厚,传递函数近似导致的光学常数的偏差越小。 2.5 光学常数的合成不确定度 2.1 ~2.4节分析了太赫兹光谱测量液体光学常数时的4种误差来源对于测量不确定度的贡献。它们对于样品折射系数和吸收系数的合成不确定度可以表示为 其中包含因子kp=1表示标准不确定度,kp>1表示扩展不确定度。NE表示太赫兹信号的测量次数;Nl0表示比色皿厚度的测量次数分别表示幅值测量、比色皿倾斜、传递函数近似和光程公差导致的测量样品折射系数(吸收系数)的不确定度分量。因为这些误差来源都是不相关的,所以在公式中没有出现协方差项。 式(27)、式(28)建立了太赫兹光谱测量液体光学常数的不确定分析模型。通过该模型可以比较不同实验室测量结果的准确性。除此之外,该模型还可以用来分析系统主要的误差来源从而优化测量过程。 为了验证建立的不确定度分析模型的有效性,选择塑化剂样品(DEHP)进行太赫兹时域光谱实验。系统采用的锁模飞秒脉冲光纤激光器的重复频率为80MHz,脉冲宽度32 fs,平均功率280mW,中心波长1570nm。所产生的太赫兹脉冲信号的动态范围60dB,带宽0.2~3THz。为了消除水蒸气的影响,太赫兹光路充满洁净干燥的空气使相对湿度在3%以下。 3种太赫兹光谱的时域信号交替测量5次。5次测量的平均值的以及各自的标准偏差如图4所示,其中插图显示的是均值信号的频谱。 图4 实验测得的3种太赫兹信号分别测量5次的平均值及标准差 图5 DEHP光学常数测量的不确定度及各个误差分量的不确定度 用游标卡尺测得的比色皿厚度的平均值为1.16mm。假定入射角偏差在[-5°,5°]并服从矩形分布。在整个测量过程中,环境相对湿度为60%,环境温度为25℃,对应于空气的折射率为1.0001。 图5表明DEHP的折射率和吸收系数的测量不确定度量级分别为0.01和1 cm-1,DEHP的折射率在n=1.51左右。吸收系数随着频率的增加从5 cm-1增加到30cm-1。幅值测量误差相关的不确定度分量sn,E和sα,E在高频时变得较大,可能是因为太赫兹波的高频分量更容易受到反射镜的位置和方向误差的影响。图5(a)表明,折射率的不确定度的最大误差来源是样品厚度的不确定性。幅值测量的标准偏差在1.1THz以下的值约为折射率的1/10000,其影响可以忽略。传递函数近似导致的不确定度fn,H随着频率的增加而变小。图5(b)表明吸收系数的不确定度的最大误差来源是信号噪声(高频段),和传递函数近似(低频段);其次的误差来源是比色皿厚度的不确定性sα,l0;样品厚度的偏差(以fα,l表示)和倾斜角对应的偏差(以fα,θ表示)相对较小;游标卡尺的分辨率造成的系统误差sα,δ非常小,可以忽略。 本文建立THz-TDS透射式系统用于测量液体样品时的不确定度分析模型,确认影响测量结果的4种误差来源,得到了这些误差的方差或偏差与样品光学常数测量结果的方差或偏差关系的解析公式。不同实验室可以在这个基础上对液体样品测量结果进行比较。该不确定度分析模型的一大优点是它可以用于分析测量参数的灵敏度以及优化测量参数使得不确定度减小。此外,该模型没有考虑样品相关的误差来源,如散射效应或样品可能的非均匀性,以及样品引起的太赫兹波束聚焦形状变化(焦点的束腰、瑞利长度以及波形发散等),这些情况的不确定度分析模型可在今后的工作中进一步研究。 [1]JEPSEN P U,COOKE D G,KOCH M.Terahertz spectroscopy and imaging:Modern techniques and applications[J].Laser Photon Rev,2011,5(1):124-166. [2]FISCHER B M,HELM H,JEPSEN P U.Chemical recognition with broadband THz spectroscopy[J].Proceed ings of the IEEE,2007,95(8):1592-1604. [3]JEON,TAE I,GRISCHKOWSKY D.Characterization of optically dense,doped semiconductors by reflection THz time domain spectroscopy[J].Applied Physics Letters,1998,22(23):3032-3034. [4]卢承振,刘维,孙萍,等.不同水的太赫兹时域光谱[J].激光与光电子学进展,2015,52(4):254-261. [5]WALTHER M,FISCHER B,SCHALL M,et al.Farinfrared vibrational spectra of all-trans,9-cis,and 13-cis,retinal measured by THz time-domain spectroscopy[J]. Chemical Physics Letters,2000,332(3-4):389-395. [6]NAKANISHI A,KAWADA Y,YASUDA T,et al.Terahertz time domain attenuated total reflection spectroscopy with an integrated prism system[J].Review of Scientific Instruments,2012,83(3):97. [7]REID C B,REESE G,GIBSON A P,et al.Terahertz time-domain spectroscopy of human blood[J].IEEE Transactions on Terahertz Science&Technology,2013,3(4):363-367. [8]NAFTALY M.Metrology issues and solutions in THz timedomain spectroscopy:Noise,errors,calibration[J].IEEE Sensors Journal,2013,13(1):8-17. [9]HÜBERS H W,KIMMITT M F,HIROMOTO N,et al. Terahertz spectroscopy:System and sensitivity consideration[J].IEEE Trans Terahertz Sci Technol,2011,21(1):321-331. [10]HIROMOTO N,TRIPATHI S R,TAKEDA M,et al. Study on random errors in THz signal and optical constants observed with THz time-domain spectroscopy[C]∥Proc 35th Int Conf Infrared Millim Terahertz Waves,2010. [11]DUVILLARET L,GARET F,COUTAZ J L.In fluence of noise on the characterization of materials by terahertz time-domain spectroscopy[J].J Opt Soc Amer,2000,17(3):452-461. [12]WITHAYACHUMNANKUL W,FISCHER B M,LIN H,et al.Uncertainty in terahertz time-domain spectroscopy measurement[J].JOpt Soc Amer,2008,25(6):1059-1072. [13]WITHAYACHUMNANKUL W,LIN H,MICKAN S P,et al.Analysis of measurement uncertainty in THz-TDS[C]∥Proc SPIE,2007. [14]李向军,杨晓杰,刘建军.基于反射式THz时域谱的水THz光学参数测量与误差分析[J].光电子激光,2015(1):135-140. [15]SOLTANI A,JAHN D,DUSCHEK L,et al.Attenuated total reflection terahertz time-domain spectroscopy:Uncertainty analysis and reduction scheme[J].IEEE Trans Terahertz Sci Technol,2016,6(1):32-39. [16]WITHAYACHUMNANKUL W,NAFTALY M.Fundamen tals of measurement in terahertz time-domain spectroscopy[J].Journal of Infrared Millimeter and Terahertz Waves,2014,35(8):1-28. [17]LIU L P,SHEN L,YANG F,et al.Determining phthalic acid esters using terahertz time domain spectroscopy[J]. Journal of Applied Spectroscopy,2016,83(4):1-7. (编辑:李刚) Analysis of measurement uncertainty in determ ining liquids’optical constants by terahertz time-domain spectroscopy ZHANG Fang1,YANG Fei2 To build an uncertainty analytical model for measurement of optical constants of liquid sample by terahertz(THz)time domain spectroscopy,the measurement equations are derived by taking THz transmission system with a cuvette as its sample cell into account.The sources contributing to the measurement error,including the errors in T-ray amplitude,sample thickness,cuvette thickness,cuvette tilting,and systematic error in approximated transfer function,are identified.The error propagation through the measurement process is modeled.The analytical formula representing the relation between a source uncertainty and the output uncertainty is derived.An actual experiment is carried out to obtain the refractive index and absorption coefficient of a Di 2-ethyl hexyl phthalate(DEHP)sample.Their uncertainty is calculated with an order of 0.01 and 1 cm-1,respectively.The results show that the uncertainty model can be the basis for assessing the measurement accuracy of the optical constants. THz;spectroscopy;measurement uncertainty;cuvette;optical constant;error propagation A 1674-5124(2017)05-0030-06 10.11857/j.issn.1674-5124.2017.05.007 2016-09-20; 2016-11-18 贵州省科学基金(J20142107);贵阳职业技术学院科研项目(GYZGY2016YB-36) 张放(1986-),女,贵州贵阳市人,讲师,硕士,研究方向为药物分析、傅里叶红外光谱、太赫兹光谱分析。 杨霏(1986-),男,重庆市人,高级工程师,博士,主要从事计量、太赫兹光谱分析的研究工作。
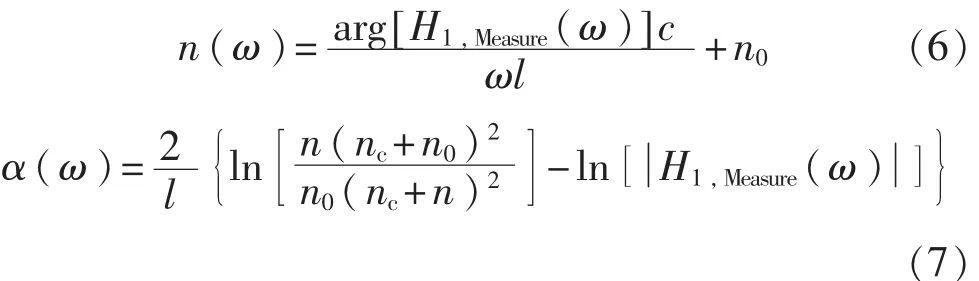
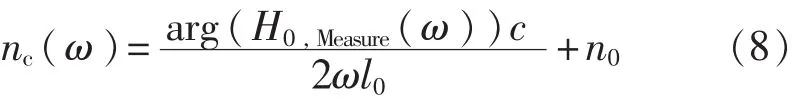
2 误差来源及不确定度分析

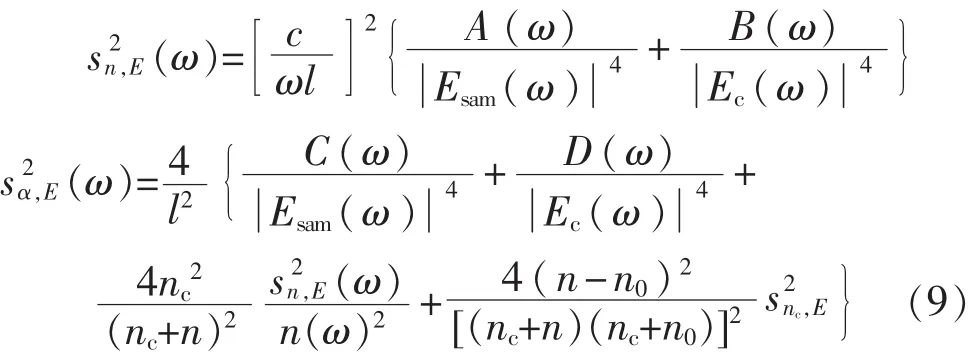


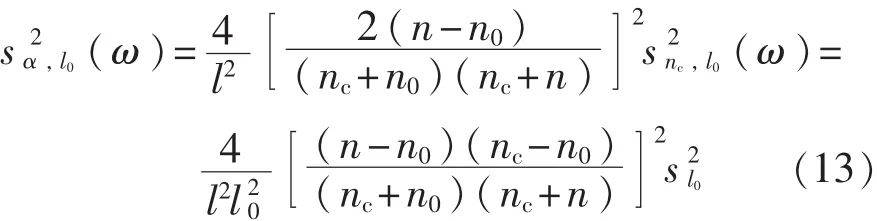


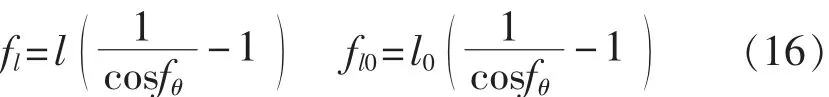





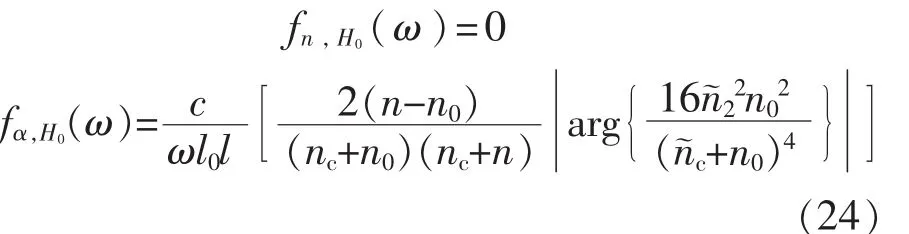
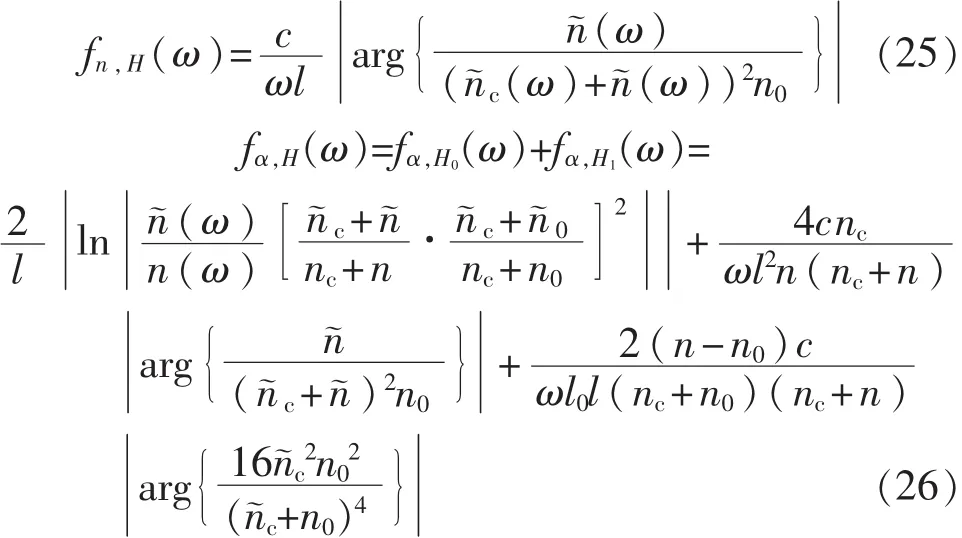

3 太赫兹时域光谱测量实验

4 结束语
(1.Biochemical Engineering Department,Guiyang Vocational and Technical College,Guiyang 550023,China;2.Guizhou Institute of Metrology,Guiyang 550003,China)
