装甲车辆用立式弹药舱的设计与动力学分析
2017-06-08张雷雨李剑锋杨洋
张雷雨, 李剑锋, 杨洋
(1.北京工业大学 机械工程与应用电子技术学院, 北京 100124;2.北京航空航天大学 机械工程及自动化学院, 北京 100191)
装甲车辆用立式弹药舱的设计与动力学分析
张雷雨1, 李剑锋1, 杨洋2
(1.北京工业大学 机械工程与应用电子技术学院, 北京 100124;2.北京航空航天大学 机械工程及自动化学院, 北京 100191)
为分析输送链条的动力学特性和弹药的稳定性,将所有链节及弹架两侧双排滚子简化为弹簧阻尼单元,采用多体系统动力学和运动弹性动力学理论,建立输送链条的完整动力学模型和弹药的稳定性模型。借助Matlab软件,对输送链条的整体动力学模型进行数值仿真,并求解弹药的稳定性模型。通过数值仿真结果可知:在不同驱动功率下输送链条的速度、加速度均窄幅波动;轨迹线的形状特征决定了弹药离心力的动力学响应和突变特性,离心力的突变特性对弹药运动法线方向稳定性具有较大的影响,而弹药在运动切线方向上的稳定性主要受自身惯性和输送链条的动力学参数影响。根据弹药上部的摆动位移响应可知,弹药在运动法线方向和切线方向具有较好的动态稳定性。采用试验测量方法,得到输送链条的切线方向加速度与弹架的法线方向加速度值,测量数据与仿真结果较为吻合。
兵器科学与技术; 立式弹药舱; 输送链条; 弹簧阻尼系统; 多体系统动力学; 稳定性
0 引言
自动弹药舱作为弹药装填系统的核心组件,具有弹药存储、弹种识别和自动选弹的功能,而坦克等装甲车辆的内部空间异形且狭窄,如何在异形空间约束下进行自动弹药舱的设计和放置成为重大挑战,且弹药运动路径规划、动力学特性及稳定性分析已成为兵器技术领域的重要研究方向。
目前,俄罗斯T64A/T72/T90A及中国96A/99式坦克采用盘状弹药舱[1],分装式弹丸和药筒平放在炮塔吊篮底板下方,采用转盘式的驱动方式。法国“勒克莱尔”、日本90式及部分美国M1A1、德国“豹Ⅱ”坦克的自动弹药舱位于炮塔的尾舱中[2],整装式弹药平放于弹药舱内的弹匣内,采用链条系统拖动弹药循环运动。美国TCM公司装甲火炮系统(AGS)的自动装弹机位于炮塔下方吊篮内[3],弹药舱采用带状结构,在竖直放置弹药的顶部及底部均设置了拖动链条。针对125 mm整装式弹药,本文提出并设计了装甲车辆用立式弹药舱,放置于吊篮内部的左侧。基于弹药舱的功能和吊篮内部异形空间的特征,进行弹药运动路径规划和传动系统的设计,实现有限空间中存储最大数量的弹药。
由于吊篮内部空间异形且狭窄,弹药运动路径不规则[4],采用链传动作为立式自动弹药舱的动力输送方式。国内外学者对链传动的研究越来越完善和详尽,Chew[5]将滚子链中各链节的质量简化至滚子中心,采用归纳法,推导出整根链条的等效质量公式,得到链条惯性对链节间冲击强度的影响。Troedsson等[6-7]着重分析链传动中静载荷的分布和链条振动问题,将链节等效为具有弹簧阻尼特性的弹性链板。Zheng等[8]采用显式有限元方法,建立了链传动的全尺寸模型,分析了滚子链的机械特性和啮合时的瞬态振动响应。Xu等[9-10]和Spicer[11]在建立滚子链动力学模型时,考虑了输入轴弹性和链节弹簧阻尼性的影响,但分析的链节数量较少,未将动力学模型拓展至包含实际数量链节的封闭链条。借鉴上述分析方法,将输送链条所有链节的弹簧阻尼性考虑在内,建立链条拖动系统的完整动力学模型,分析弹药竖直放置且单点拖动时动态稳定问题。
1 立式弹药舱的结构
1.1 弹药轨迹线及输送链条优化
立式弹药舱放置于吊篮内部的左侧,可用空间为座圈、炮膛及隔爆板组成的几何空间,同时需避开炮尾的反后坐装置,可用空间由多个圆弧和直线段组成,呈狭长状,属于异形空间,如图1所示。

图1 放置弹药舱的可用空间Fig.1 Available space for ammunition cabin
设计立式弹药舱时,需明确弹药、弹匣、炮塔等边界约束。为了保护弹药及提高弹药存放的适应性,针对不同弹药的外形尺寸设计了通用型弹匣,在弹药布置方案中以弹匣直径dc为基准进行规划,炮塔内部直径db与炮塔座圈直径ds相等,续弹舱外侧轮廓半径rm小于炮塔座圈半径(ds/2),见图1.
弹药均匀分布在轨迹线上,在满足多边界约束的条件下,以布置最大数量的弹药为优化目标,建立轨迹线的分段函数模型,采用参数法和遗传算法进行优化,得到轨迹线的最佳形态,如图2所示。轨迹线由4段圆弧和2条线段组成,圆弧与线段间均采用相切过渡,输送链条的链节分布在轨迹线上,链条节距p=57.15 mm,链条型号为36A,封闭的输送链条由48个链节构成,能够拖动12枚弹药沿轨迹线循环运动。

图2 轨迹线的组成Fig.2 Elements of ammunition trajectory
1.2 立式弹药舱的结构设计
基于轨迹线的形态设计内、外底板,内、外底板形成组合式环形导向轨道和负载轨道。导向轨道用于约束输送链条严格沿轨迹线分布,负载轨道承载弹架、弹匣和弹药的重力及受到的倾覆力矩,如图3所示。弹架的下部与输送链条通过螺纹连接,弹药与弹匣均放置在弹架上,电机驱动输送链条,沿导向轨道循环往复运动。当选定的弹药输送至举升位置时,锁紧机构在电磁铁的驱动下将输送链条和弹架锁紧并固定。

图3 弹药舱的驱动系统Fig.3 Drive system of ammunition cabin
弹药放置在通用型弹匣中,弹匣插接在弹架上,弹匣锁紧机构将弹匣与弹架锁紧为一体,如图4(a)所示。弹架两侧设置了双排滚子,弹架通过双排滚子卡装在底座的负载轨道上,弹架的上部和输送链条下部均安装有导向轮,导向轮与导向轨道接触,减小弹架与输送链条的运动阻力,同时确保循环链条沿轨迹线分布,如图4(b)和图4(c)所示。

图4 弹架与弹匣的结构Fig.4 Structures of ammunition rack and cartridge
立式弹药舱中的输送链条仅拖动弹药的底部,在弹药舱启动及运动的过程中,弹药及弹匣的稳定性受惯性力、翻转力矩及轨迹线几何特征的影响较大,因此,输送链条的动力学特性和弹药的稳定性是本文的研究重点。
2 立式弹药舱的动力学建模
将弹药、弹匣和弹架作为单个负载单元,综合多刚体系统动力学和柔性多体系统动力学理论,将所有链节及负载单元作为弹簧阻尼单元处理[12],建立单个负载单元的通用动力学模型,其次,建立输送链条各链节的动力学模型,进而建立弹药舱的全动力学模型。采用运动弹性动力学方法,构建竖直的弹药稳定性模型,根据弹药上部摆动位移响应情况,分析弹药的稳定性问题。
2.1 负载单元的动力学建模
为了精确分析弹药在运动过程中的上部摆动位移及由此引起的干涉问题,将弹药、弹匣简化为刚性杆,将链节的质量m集中在链节的滚子中心上,输送链条即被简化为一串铰接的质点。


图5 负载单元i的力学模型Fig.5 Force model of load unit i

(1)


(2)

(3)
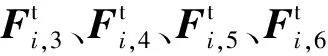

(4)
式中:A、B为简化系数,


2.2 输送链条的动力学建模
输送链条是续弹舱的动力执行元件,整条滚子链在运动过程中的长度随着受力的变化而变化。将链条假设为弹性体,每个链节简化为无质量弹簧阻尼单元。输送链条共由N(N=48)个链节组成,链节j的质量mj集中在滚子中心上,如图6(a)所示,链节1(j=1)拖动弹药1(i=1),链节j与弹药i的对应关系须满足j= 4(i-1)+1.

图6 输送链条的简化模型Fig.6 Simplified model of drive chain

(5)


(6)
式中:γj,b为沿轨迹线切线方向的速度vj与线段OjOj-1的夹角;γj,a为速度vj与线段Oj+1Oj的夹角。

(7)
联立负载单元和输送链条的动力学方程,建立输送链条的整体动力学模型,根据初始条件和动力输入,求解输送链条及弹药的动力学响应。
2.3 弹药的稳定性模型
弹匣刚度大且受力均匀,在外部冲击下不易产生应力集中和变形,因此,弹匣、弹药作为刚体处理。弹架两侧双排滚子的受力较大,将双排滚子简化为弹簧阻尼单元,弹药的转动中心为双排滚子的几何中心Ot,如图7所示。

图7 负载单元i的弹簧阻尼模型Fig.7 Spring-damping model of load unit i
在运动轨迹线的法线方向上,弹药摆动的转角为θy,由相对于中心Ot的力矩平衡方程可得弹药的运动微分方程:

(8)


(9)
式中:C为关于速度和轨迹线半径的函数,
同理,可推导出弹药在运动轨迹线切线方向上转角θx的2阶微分方程:

(10)
式中:cx、kx分别为双排滚子沿运动切线方向的阻尼系数和弹簧系数;Jx为弹药和弹匣在运动切线方向的转动惯量;D为关于速度等的函数,
弹药上端产生的切线方向摆动位移xi(t)和法线方向摆动位移yi(t)分别为
(11)
式中:lb为弹药顶端距离点Ot的距离。
3 仿真结果分析及试验对比
立式弹药舱的动力学方程分为3个部分:负载单元的动力学模型、输送链条的动力学模型及弹药的稳定性模型,借助Matlab软件,采用龙格- 库塔法进行求解。将主要参数初始值等代入至程序中,得到立式弹药舱的动力学响应,立式弹药舱的主要参数如表1所示。



表1 立式弹药舱的主要参数Tab.1 Main parameters of vertical ammunition cabin
在续弹舱满负载情况下,仿真不同功率Pd下的链节1的速度v1,如图8所示。在恒功率(Pd=500 W)的驱动下,速度v1经历了迅速上升、缓慢上升、波动平衡3个阶段。由图8可知,随着驱动功率Pd增加,速度v1到达平稳波动的加速时间逐渐减小,速度v1的平稳波动速度值逐渐提高。在不同功率下速度震荡幅度λ接近,且幅度λ<0.4 m/s. 由图8(c)可知,当功率Pd=1 000 W时,v1≈0.61 m/s,与实际试验测量数据较为吻合。

图8 在不同功率Pd下的速度v1Fig.8 Velocity v1 nder different power Pd


图9 在不同功率Pd下的加速度1Fig.9 Acceleration 1 under different power Pd
3.2 弹药i受到的离心力Fy,i
弹药和弹匣在竖直放置状态下,重心位置偏高,离心力Fy,i对弹药的稳定性影响较大,以弹药1受到的离心力Fy,1为研究对象,同时,设定Pd=1 000 W,以分析Fy,1对弹药1稳定性的影响。
图10为离心力Fy,1的响应曲线,数值仿真的起点为举升位置,输送链条顺时针方向运动,弹药1沿线段1运动至圆弧4,沿圆弧4运动至线段2,再由线段2到圆弧1、圆弧2、圆弧3,最后,从圆弧3回到线段1即举升位置(见图2)。结合轨迹线的形状特征,由图10(a)可知,离心力Fy,1产生于圆弧4、圆弧1、圆弧2、圆弧3,Fy,1的大小与速度v1及圆弧半径密切相关。在线段1和线段2上离心力Fy,1为0 N,弹药1在圆弧4上的速度v1处于震荡上升阶段,Fy,1的最大值出现在圆弧3上。

图10 在不同负载下的离心力Fy,1Fig.10 Centrifugal force Fy,1 under different loads
由图10可知,随着各弹药负载ma的负载减小,离心力Fy,1逐步减小,Fy,1在不同圆弧上的大小差距减小。由离心力Fy,1的响应曲线和突变特性可推测:离心力Fy,1的突变导致了速度v1趋于稳定后一直处于波动状态,且Fy,1的突变由轨迹线的形状特征决定。
3.3 弹药的稳定性分析

图11 弹药1的法线方向角速度yFig.11 Normal angular velocity y of Ammunition 1
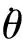
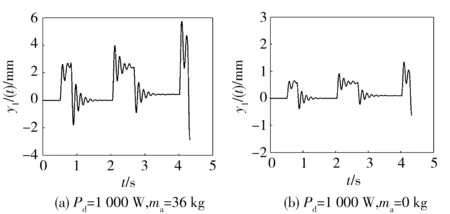
图12 弹药1的法线方向摆动位移y1(t)Fig.12 Normal vibration displacement y1(t) of Ammunition 1
由上述分析可知,弹药在运动法线方向上的弹性振动主要由离心力Fy,1所导致,在离心力的突变位置激起弹匣运动法线方向的弹性振动,且弹性振动幅值随着运动速度、负载重量的增加而加大。在弹匣满载的情况下,弹药的摆动位移y1(t)最大幅值为5.6 mm,弹匣与弹药舱外侧板预留间隙为6 mm,满足设计技术要求。
图13为弹药1的切线方向摆动位移x1(t),弹药1在运动过程中一直处于摆动状态,摆动位移x1(t)在零位附近上下波动,在弹匣空载状态(ma=0 kg)x1(t)依旧上下震荡,但振动范围大幅缩小。摆动位移x1(t)在[-1.5 m,1.5 m]内波动,满足弹药之间最大摆动位移量要求,弹匣在运动切向具有良好的稳定性特征。

图13 弹药1的切线方向摆动位移x1(t)Fig.13 Tangential vibration displacement x1(t) of Ammunition 1
3.4 试验对比
设计动力学验证试验,验证所建立的整体动力学模型正确性。试验方案:采用两个加速度传感器(CA-YD-187)测量输送链条在运动切线方向和法线方向的加速度响应。两传感器垂直正交地固定在安装支架上,如图14所示,将安装支架固定在弹药下部的弹架上,弹架与输送链条固连,通过测量弹架的加速度等效为输送链条的动力学参数。

图14 加速度传感器的安装示意图Fig.14 Installation diagram of acceleration sensors


图15 输送链条的切线方向加速度TFig.15 Tangential acceleration T of drive chain



图16 弹架的法线方向加速度NFig.16 Normal acceleration N of ammunition rack
4 结论
1)建立单个负载单元的通用动力学模型,将输送链条的链节均简化为弹簧阻尼单元,构建输送链条的整体动力学模型。根据输送链条的动力学参数,采用运动弹性动力学方法,建立竖直放置弹药的稳定性模型。



References)
[1] 郭正祥. T-72C坦克的自动装弹机(下)[J]. 国外坦克, 1996(8): 27-31. GUO Zheng-xiang. Autoloader of tank T-72C(2)[J]. Foreign Tank, 1996(8):27-31. (in Chinese)
[2] George, E.Mauser. 装甲火炮系统自动装弹机[J]. 国外坦克, 1996(12): 20-24. George E M. Autoloader of armored gun system[J]. Foreign Tank, 1996(12):20-24. (in Chinese)
[3] Christopher F Foss. 装甲战车的自动装弹机[J]. 国外坦克,1996(5): 24-28. Foss C F. Autoloader of armored vehicle[J]. Foreign Tank, 1996(5): 25-28. (in Chinese)
[4] Pedersenl S, Hansenl J, Ambrósio J A C. A roller chain drive model including contact with guide-bar[J]. Multibody System Dynamics, 2004, 12(3): 285-301.
[5] Chew M. Inertia effects of a roller-chain on impact intensity[J]. Journal of Mechanisms, Transmissions, and Automation in Design, 1985, 107(1): 123-130.
[6] Troedsson I, Vedmar L. A method to determine the static load distribution in a chain drive[J]. Journal of Mechanical Design, 1999, 121(3): 569-579.
[7] Troedsson I, Vedmar L. A method to determine the dynamic load distribution in a chain drive[J]. Proceedings of the Institution of Mechanical Engineers. Part C: Journal of Mechanical Engineering Science, 2001, 215(5): 569-579.
[8] Zheng H, Wang Y Y, Quek K P. A refined numerical simulation on dynamic behavior of roller chain drives[J]. Shock and Vibration, 2004, 11(5/6): 573-584.
[9] Xu L X, Yang Y H, Chang Z Y, et al. Clearance influence on dynamic response of intermittent roller chain drive[J]. Chinese Journal of Mechanical Engineering, 2010, 23(6): 699-708.
[10] Xu L X, Yang Y H, Chang Z Y,et al. Dynamic modeling of a roller chain drive system considering the flexibility of input shaft[J]. Chinese Journal of Mechanical Engineering, 2010, 23(2): 1-8.
[11] Spicer J B. Effects of the nonlinear elastic behavior of bicycle chain on transmission efficiency[J]. Journal of Applied Mechanics, 2013, 80(2):599-605.
[12] Zhang L Y, Yang Y. A numerical simulation on dynamic behavior of pushing chain mechanism[J]. Proceedings of the Institution of Mechanical Engineers. Part C: Journal of Mechanical Engineering Science, 2016, 230(11):1902-1909.
Design and Dynamics Analysis of Vertical AmmunitionCabin for Armored Vehicle
ZHANG Lei-yu1, LI Jian-feng1, YANG Yang2
(1.College of Mechanical Engineering and Applied Electronics Technology, Beijing University ofTechnology, Beijing 100124, China;2.School of Mechanical Engineering and Automation, Beihang University, Beijing 100191, China)
The vertical ammunition cabin possesses the functions of ammunition storage, recognition and automatic selection. The ammunition vertically placed in the cabin is circularly dragged along the optimum ammunition trajectory by the drive chain. In order to analyze the dynamic properties of drive chain and the stability of ammunition, all links of drive chain and the double-row rollers of ammunition rack are simplified as spring-damper elements. The full dynamics models of drive chain and the stability model of ammunition are established by use of multi-body dynamics and kineto-elastodynamics methods. A numerical simulation of the full dynamics models is performed by adopting Matlab software. The stability model of ammunition is solved. Simulated results show that the velocity and acceleration of drive chain fluctuate within a small range. The dynamic response and drastic characteristic of centrifugal forces are dominated by the shape feature of the trajectory. The normal stability of ammunition is influenced by the drastic characteristic. The tangential stability is determined by the inertia forces of ammunition and the dynamic parameters of drive chain. The analysis shows that the ammunition has high normal and tangential stability. The tangential accelerations of chain and the normal accelerations of ammunition rack are measured. It can be found that the measured data are consistent with the simulated results.
ordnance science and technology; vertical ammunition cabin; drive chain; spring-damping system; multi-body dynamics; stability analysis
2016-08-16
中国博士后科学基金项目(2016M600021); 国家自然科学基金项目(61273342、51675008)
张雷雨(1988—), 男, 讲师, 博士。 E-mail: zhangleiyu1988@126.com
李剑锋(1964—), 男, 教授, 博士生导师。 E-mail: lijianfeng@bjut.edu.cn
TJ810.2
A
1000-1093(2017)05-0843-09
10.3969/j.issn.1000-1093.2017.05.002
