定向射孔参数对压裂裂缝扩展规律的影响

陈军斌，魏波，王汉青

（1.西安石油大学石油工程学院，陕西 西安 710065；2.中国石油塔里木油田分公司油气工程研究院，新疆 库尔勒 841000）

定向射孔参数对压裂裂缝扩展规律的影响

陈军斌1，魏波2，王汉青1

（1.西安石油大学石油工程学院，陕西 西安 710065；2.中国石油塔里木油田分公司油气工程研究院，新疆 库尔勒 841000）

为了探究直井水力压裂过程中定向射孔参数对压裂裂缝扩展规律的影响，采用扩展有限元方法对水压致裂岩石的流固耦合模型进行求解，从射孔方位、射孔长度和射孔相位角3个方面分析了裂缝自射孔孔眼起裂的扩展和转向规律。研究结果表明：射孔方位对裂缝周围地层压力分布几乎没有影响；射孔方位角较小的孔眼具有较低的起裂压力和较高的扩展压力，压裂后容易形成长而宽的裂缝；射孔方位角较大的孔眼则具有较高的起裂压力和较低的扩展压力，压裂后容易形成短而窄的裂缝；随着射孔长度的增加，重新定向距离逐渐增长，在转向处易形成相对较宽的裂缝；射孔相位角过小容易引发裂缝干扰，射孔方位角较小的裂缝优先扩展并对后扩展的裂缝产生较强的抑制作用。在施工时，为获得较好的改造效果，应尽量选择小方位射孔；为避免缝间干扰，射孔相位角应大于45°。

水力压裂；定向射孔；数值模拟；扩展有限元

0 引言

射孔参数的选取对水力压裂设计具有重要意义。在远场地应力、井筒效应和射孔方位的影响下，裂缝从射孔处起裂，形成具有一定曲率的裂缝，其曲率取决于射孔方位与平面最大主应力夹角的大小。Abass等［1-2］基于物理模拟实验指出，在直井或水平井条件下，破裂压力总随射孔方位角的增加而增加。姜浒等［3］则通过大尺度真三轴水力压裂物理模拟实验，探究了射孔方位和水平应力差对地层破裂压力与裂缝形态的影响。实验模拟形象直观地揭示了定向射孔水力压裂裂缝扩展的一般规律，对于指导实际射孔参数优化设计具有重要参考意义。但实验模拟费时费力，因而，近年来数值模拟在探究水力压裂相关规律方面得到了更为广泛的应用。

有限元方法是近些年来模拟水力压裂裂缝扩展的常用方法［4-6］；但其在求解时，裂缝路径需要预先设定，无法体现裂缝的转向规律及裂缝扩展的任意性，且在每个时间步结束后均需对裂缝重新进行网格划分，进而影响网格精度和计算效率。扩展有限元法则弥补了有限元法在模拟裂缝扩展时的缺陷［7］。Sepehri等［8］基于扩展有限元法模拟了不同射孔方位、水平应力差条件下的裂缝扩展形态，并与Abass的实验结果进行了对比。现阶段学者们运用扩展有限元方法在定向射孔对裂缝起裂压力与转向距离的影响方面开展了大量的研究，但对裂缝扩展过程中的压力分布、流体变化以及缝宽的影响研究相对较少。本文运用扩展有限元法求解基于最大拉应力准则与应力强度因子准则建立的水压致裂岩石的耦合模型，研究了不同射孔方位、射孔长度和射孔相位角对裂缝起裂与扩展的影响。

1 水力压裂扩展有限元模型

1.1 水力压裂的耦合分析

水力压裂是黏性流体流动与岩体变形、破裂的动态耦合过程。借助Abaqus6.14软件耦合求取岩石变形的应力平衡方程与连续性流动方程，进而模拟井筒附近地层岩石在流体压力作用下的破裂过程。

岩体变形的应力平衡方程弱形式［9］为

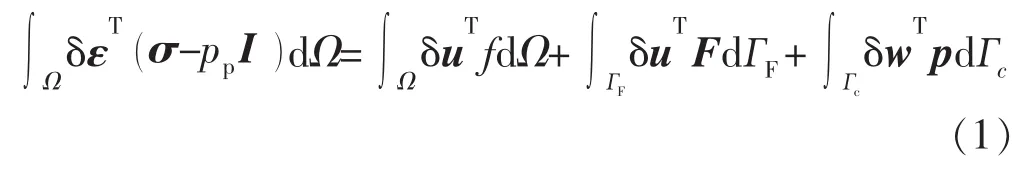
式中：Ω为二维扩展域；ГF，Гc分别为外力边界与裂缝边界；δ为为克罗内克符号；ε为虚应变矩阵；σ为有效应力矩阵；pp为岩体孔隙压力，Pa；I为单位矩阵；u为虚位移矩阵；f为体积力，Pa；F为外力矩阵；w为裂缝张开位移矩阵；p为裂缝内流体压力矩阵。

裂缝内流体流动的连续性方程弱形式［10-11］为

式中：ws为裂缝宽度，m；▽为哈密顿算子；μ为流体黏度，Pa·s；t为时间，s；ql为流体滤失量，m3。

1.2 基于扩展有限元的水力压裂裂缝描述

扩展有限元是在有限元的基础上添加裂缝间断形函数与额外自由度对裂缝位移场进行描述的［12］。被裂缝完全贯穿的单元，裂缝面两侧的节点位移发生了跳跃，可用阶跃形函数H（x）表示为

没有被裂缝完全贯穿的单元 （裂缝尖端止于单元内），裂尖周围的节点可用裂缝尖端形函数B（x ）表示：

扩展有限元格式的裂缝周围位移场的近似式为

式中：In为网格中所有节点的集合；Icr为被裂缝完全贯穿的节点集合；Itip为裂尖的单元节点集合；Ni（x）为单元节点形函数；Nj（x ）为单元中含有间断的节点形函数；ui为位移节点自由度；aj与为分别模拟裂缝路径与尖端的额外节点自由度。

裂缝内流体压力可用标准有限元法近似表示为

射孔孔眼处裂缝的起裂准则满足最大拉应力准则，即最大主应力达到岩石的抗拉强度时，孔眼处岩石发生破裂：

式中：σmax为最大主应力，Pa；σt为岩石抗拉强度，Pa。

裂缝扩展的判断依据是满足岩石失稳条件，即应力强度因子达到其断裂韧性时，岩石失稳扩展：

式中：KI为应力强度因子，MPa·m1/2；KIC为岩石断裂韧度，MPa·m1/2。

2 模型设计与参数选取

建立定向射孔裂缝扩展模型（见图1）。为了满足计算精度，采用四节点矩形单元对模型进行网格划分，并引进沙漏控制计算的收敛性。模型边界为封闭固定边界，射孔方位角θ的取值范围为0～90°，裂缝内流体满足连续性方程，不考虑流体的滞后。井筒周围受到流体压力、水平地应力以及孔隙压力的作用。

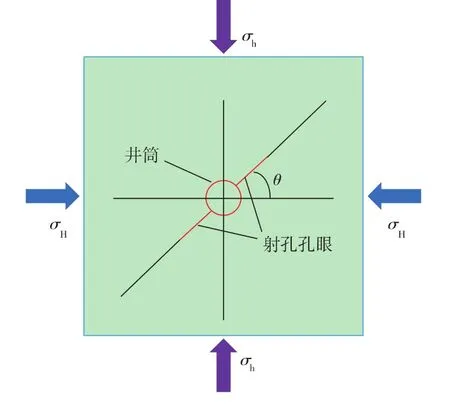
图1 模型示意

基本模拟参数见表1。设计2套模拟实验方案：第1套方案的数据选取陈勉等［3］的实验数据，用于数值模拟结果与物理模拟实验对比；第2套方案的数据选取鄂尔多斯盆地延长组某区块，用于表征实际地层环境。

表1 模拟参数

3 模拟结果及影响参数分析

3.1 模拟验证

为了验证数值模拟结果的准确性，选取60°方位角射孔进行模拟，模拟结果如图2所示，裂缝形态与实验结果具有较好的匹配性。裂缝先从射孔孔眼处起裂，并最终沿着最大主应力方向扩展，形成具有一定弯曲度的裂缝。

3.2 定向射孔特征参数分析

3.2.1 射孔方位

射孔方位角对于裂缝起裂和最终形态具有重要影响［13］。根据前人研究结果，对于要求产生明显裂缝转向的压裂，有效射孔方位角范围为30～60°［3］。因此，模拟分析了30°与60°方位角射孔条件下，地层孔隙压力、裂缝内流体压力以及缝宽和缝长随压裂时间的变化关系，模拟结果见图3—6。

图2 射孔方位角为60°时，数值模拟与实验结果对比

对比图3a与图3b可知：在30°与60°方位角射孔条件下，地层压力在裂缝周围未发生明显变化；裂缝转向内侧的地层压力值最大，近裂缝区呈尖核状分布，远离裂缝区逐渐呈椭圆状分布，且离裂缝越远，地层压力变化越小。

图3 30°与60°方位角射孔条件下地层压力分布

由图4可知，裂缝内流体压力随压裂时间快速增加，达到地层破裂压力之后，流体压力迅速降低，最终趋于平稳。当时间为0～15 s时，在井筒附近，60°射孔裂缝内的流体压力高于30°射孔内的流体压力——说明射孔方位越大，地层发生破裂所需的压力越大。随着压裂时间的增长（大于15 s），60°射孔裂缝内的压力低于30°射孔裂缝内的压力——说明60°射孔裂缝内的流体受到摩擦阻力的影响较大，阻碍了裂缝内的压力传导，造成了压力损失。

裂缝宽度与裂缝横向张开位移的关系为

式中：wf为裂缝宽度，m；u+为裂缝上表面的节点位移，m；u-为裂缝下表面的节点位移，m。

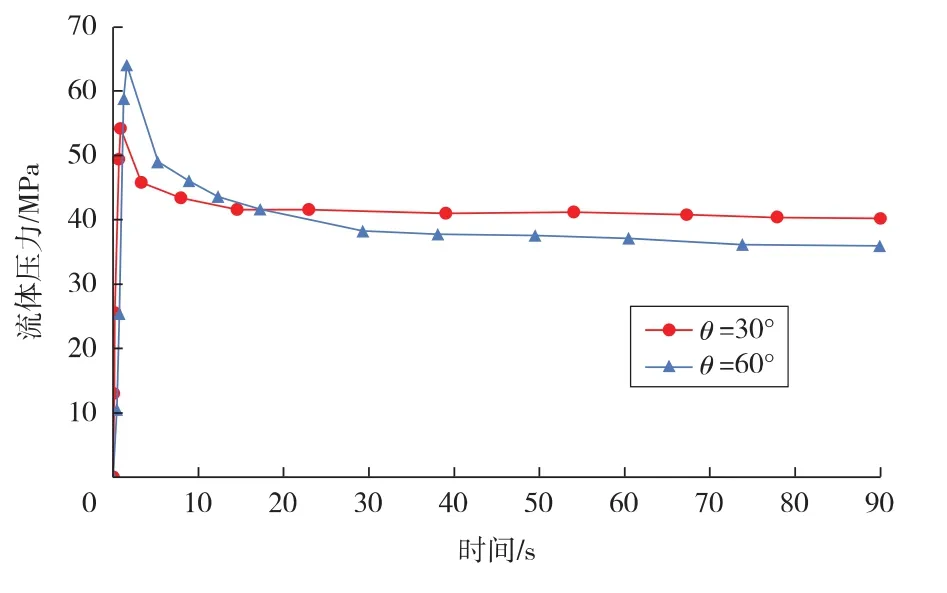
图4 裂缝内流体压力随时间的变化关系

由图5可知，无论是裂缝上表面还是裂缝下表面节点位移，30°方位角射孔的裂缝都高于60°方位角射孔的裂缝。因此，30°方位角射孔条件下的裂缝扩展宽度明显大于60°方位角下裂缝的扩展宽度。

图5 裂缝张开位移随时间的变化关系

由图6可知，30°方位角下射孔形成的裂缝长度大于60°的裂缝长度。

上述研究表明：射孔方位较小的孔眼起裂压力低，在井眼附近易形成较小曲率的裂缝，这样有利于降低注入压力和流动阻力，从而易形成长而宽的裂缝；射孔方位较大的孔眼，起裂压力高，易形成较大曲率的裂缝，压裂液在其中流动时，会产生较大的摩擦阻力与压降损失，不利于流体流动与压力传导，其结果可能导致支撑剂沉降、砂堵，甚至造成压裂施工的失败。

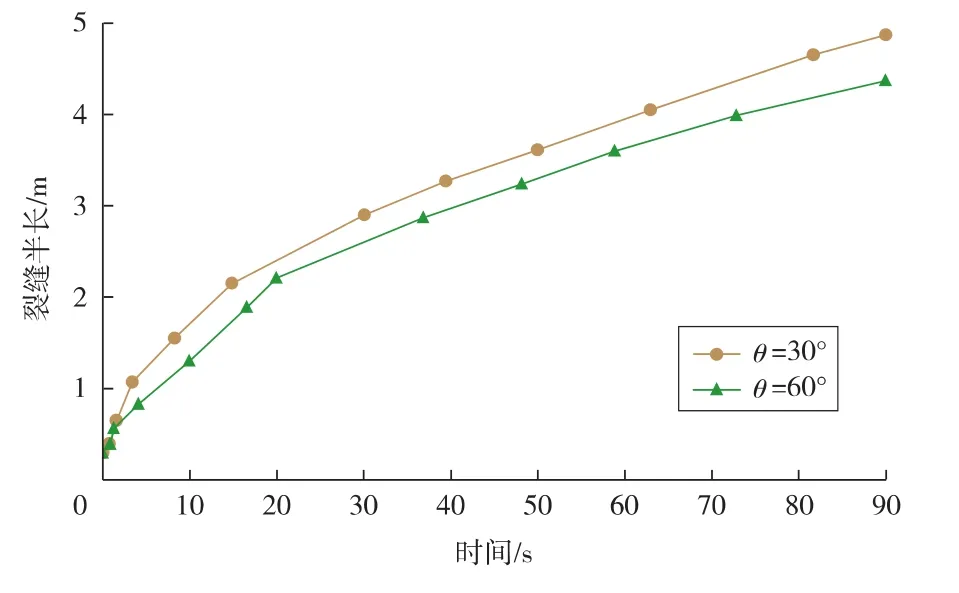
图6 裂缝半长随时间的变化关系

3.2.2 射孔长度

合适的射孔长度有利于穿过近井污染区，减小井筒效应对裂缝起裂扩展的影响［13］。选取射孔长度与井筒半径的比值，衡量射孔长度裂缝形态的影响。本文共进行6个计算模型的模拟，比值分别取1.0，1.5，2.0，3.0，4.0，5.0，射孔方位为45°。结果表明，射孔长度与井筒半径的比值越大，重新定向的距离越大，并在转向处形成较宽的裂缝，有利于压裂液的流入与支撑剂的填充。

3.2.3 射孔相位角

在压裂施工过程中，为了保证达到预期压裂效果，一般倾向于选择较小的射孔相位角，如30°，45°或60°。

当射孔相位角为30°时（见图7），优先扩展的裂缝会对后扩展的裂缝产生很强的限制作用，迫使射孔方位较大的裂缝发生不规则转向，并向低射孔方位方向延伸，从而导致不能形成有效缝长。

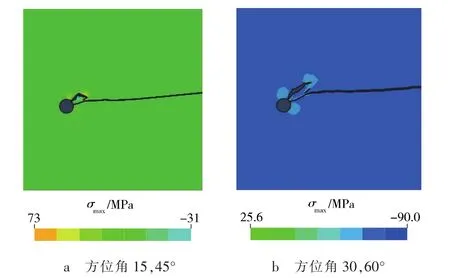
图7 30°相位角的裂缝扩展情况

当射孔相位角分别为45，60°时（见图8），则裂缝间的干扰作用显著降低。相同施工时间下，射孔方位角较小的裂缝扩展长度大于射孔方位角较大的裂缝。

通过以上分析得出：在压裂设计中，必须根据压裂施工的实际情况选择射孔相位角，相位角太小不利于形成有效的裂缝长度与宽度，并且会产生曲折度高的裂缝面，产生较高的摩擦阻力，不利于压裂液的泵入与支撑剂的填充，甚至可能会造成支撑剂沉降，最终对产量具有很大影响。从模拟结果可知，应选择大于45°射孔相位角。

4 结论

1）射孔方位对裂缝周围地层压力几乎没有影响；较大射孔方位角的裂缝具有较高的起裂压力、较低的扩展压力，易形成较窄、较短的裂缝，不利于流体流动与压力传导，因此应尽量选择小方位角射孔。

2）射孔长度越长，裂缝重新定向距离越长，在转向处易形成较宽的裂缝。

3）射孔相位越近，应力干扰作用越强，射孔方位角较小的裂缝扩展长度明显优于射孔方位角较大的裂缝，优先扩展的裂缝对后扩展的裂缝抑制作用越强。为了满足压裂设计对裂缝长度的要求，应选择大于45°射孔相位角。

［1］ABASS H H，MEADOWS D L，BRUMLEY J L，et al.Oriented perforation-A rock mechanics view［R］.SPE 28555，1994.

［2］ABASS H H，HEDAYATI S，MEADOWS D L.Nonplanar fracture propagation from a horizontal wellbore：experimental study［J］.SPE Production and Facilities，1996，11（3）：133-137.

［3］姜浒，陈勉，张广清，等.定向射孔对水力裂缝起裂与延伸的影响［J］.岩石力学与工程学报，2009，28（7）：1321-1326.

［4］BAO J Q，FATHI E，AMERI S.A coupled finite element method for the numerical simulation of hydraulic fracturing with a condensation technique［J］.Engineering Fracture Mechanics，2014，131（2）：269-281.

［5］BAO J Q，FATHI E，AMERI S.Uniform investigation of hydraulic fracturing propagation regimes in the plane strain mode［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2015，39（5）：507-523.

［6］HUNSWECK M J，SHEN Y，LEW A J.A finite element approach to the simulation of hydraulic fractures with lag［J］.International Journal for Numerical and Analytical Methods in Geomechanics，2013，37（9）：993-1015.

［7］NICOLAS M，DOLBOW J，BELYTSCHKO T.A finite element method for crack growth without remeshing［J］.International Journal for Numerical Methods in Engineering，1999，46（1）：131-150.

［8］SEPEHRI J，SOLIMAN M Y，MORSE S M.Application of extended finite element method to simulate hydraulic fracture propagation from oriented perforations［R］.SPE 173342，2015.

［9］陈军斌，魏波，谢青，等.基于扩展有限元的页岩水平井多裂缝模拟研究［J］.应用数学和力学，2016，37（1）：73-83.

［10］KRUNAL J，JOHN L.Comparison of various deterministic forecasting techniques in shale gas reservoirs［R］.SPE 163870，2013.

［11］魏波，陈军斌，谢青，等.基于扩展有限元的页岩水平井压裂裂缝扩展模拟［J］.西安石油大学学报（自然科学版），2016，31（2）：70-75.

［12］GOODARZI M，MOHAMMADI S，JAFARI A.Numerical analysis of rock fracturing by gas pressure using the extended finite element method［J］.Petroleum Science，2015，12（2）：304-315.

［13］周再乐，张广清，熊文学，等.水平井限流压裂射孔参数优化［J］.断块油气田，2015，22（3）：374-378.

（编辑 李宗华）

Influence of directional perforation parameters on fracture propagation

CHEN Junbin1,WEI Bo2,WANG Hanqing1
(1.College of Petroleum Engineering,Xi′an Shiyou University,Xi′an 710065,China; 2.Oil and Gas Engineering Research Institute,Tarim Oilfield Company,Petro China,Korla 841000,China)

In order to explore the effect of directional perforation parameters of straight well during the process of hydraulic fracturing,the laws of fracturing initiation and extension originated from perforation tunnel were analyzed in such three aspects as perforation orientation,perforation length and perforation phase angle by using extended finite element method.The results show that perforation orientation has hardly effect on the fracturing around the formation pressure distribution;long and wide fracturing is easily founded in the perforation tunnel with small orientation angle,however,it is opposite in the orientation angle with big orientation angle;with the increase of perforation length,reorientation distance increase,it is easy to form relatively wide fracture in turning point;too small perforation phase angle causes fracture interference easily,the fracture originated from perforation tunnel with smaller orientation angle extends firstly,and it has a strong inhibition on the followed fracture.In the field operation,in order to make a better stimulation,the small orientation angle should be chosen as far as possible.In order to avoid the interference of the fracture,the phase angle should be more than 45°.

hydraulic fracturing;directional perforation;numerical simulation;extended finite element

国家自然科学基金面上项目“页岩气藏水平井液态气动力压裂增产新方法研究”（51374170）；陕西省教育厅省级重点实验室项目“低渗透油藏注气（氮气、二氧化碳）提高原油采收率技术研究”（09JS036）

TE357.1

A

10.6056/dkyqt201703021

2016-11-23；改回日期：2017-03-16。

陈军斌，男，1963年生，教授，博士，主要从事油气渗流理论与提高采收率技术方面的教学和研究工作。E-mail：chenjbxu@126.com。

陈军斌，魏波，王汉青.定向射孔参数对压裂裂缝扩展规律的影响［J］.断块油气田，2017，24（3）：391-395.

CHEN Junbin，WEI Bo，WANG Hanqing.Influence of directional perforation parameters on fracture propagation［J］.Fault-Block Oil&Gas Field，2017，24（3）：391-395.