Vortex shedding in the flow around two side-by-side circular cylinders of different diameters*

Xiang Qiu (邱翔), Zhen-xiao Bi (毕贞晓), Jian-ping Luo (罗剑平), Yu-lu Liu (刘宇陆)

1. School of Science, Shanghai Institute of Technology, Shanghai 201418, China, E-mail: emqiux@163.com

2. School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418, China

3. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

Vortex shedding in the flow around two side-by-side circular cylinders of different diameters*

Xiang Qiu (邱翔)1, Zhen-xiao Bi (毕贞晓)2, Jian-ping Luo (罗剑平)2, Yu-lu Liu (刘宇陆)3

1. School of Science, Shanghai Institute of Technology, Shanghai 201418, China, E-mail: emqiux@163.com

2. School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 201418, China

3. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

2017,29(3):470-478

In this paper, the 3-D turbulent flow around two side-by-side circular cylinders of different diameters, at sub-critical Reynolds number (R e =3900), is numerically simulated by the large eddy simulation (LES). The spacing ratios (T /D ) between the two cylinders are considered in four cases (T /D =1.2, 1.5, 1.8 and 2.7) to study the vortex shedding and turbulent properties in the flow field. The main results are focused on the drag and lift coefficients, the vortex shedding frequency, the coherent structure, and the scale properties. It is shown that when T /D is equal to 1.2, the vortex shedding of the main cylinder is strongly suppressed by the small cylinder, the drag and lift coefficients of the main cylinder are smaller than those in other three cases. While T /D is equal to 1.5, the vortex shedding of the main cylinder can be improved, the drag and lift coefficients of the main cylinder are larger than those in other three cases. The empirical mode decomposition (EMD) method is applied to decompose the velocity signals traced by the LES. It is shown that there is a linear relationship between the mean period and the mode in the semi-log coordinates. The vortex shedding period of the main cylinder is consistent with the period of the restructured coherent structures quantitatively.

Large eddy simulation (LES), drag and lift coefficients, vortex shedding frequency, empirical mode decomposition (EMD)

Introduction

The flow around multiple cylinders were studied theoretically in fluid mechanics and extensively in engineering applications. As a classical model of the multiple-cylinder system, the case of two side-by-side circular cylinders attracted much attention. Experimental studies show that there are three flow patterns for the configuration of two side-by-side cylinders at different spacing ratios, including the single-bluffbody behavior, the parallel vortex streets and the biased flow pattern[1-3]. Related studies on drag and lift coefficients show that except for the biased flow regime, the mean drag coefficient is close to that of a single circular cylinder, and the mean lift coefficient isclose to zero. At very small spacing ratios, a negative lift force is on the two cylinders. Within the biased flow regime, the two cylinders are mutually expelled with positive lift coefficients[4,5].

With the development of computer technology, the flows around multiple cylinders were widely studied numerically in recent years. Kravchenko and Moin[6]studied the flow around a single circular cylinder using the large eddy simulation method at =Re 3 900. It was found that the results of the dynamic Smagorinsky sub-grid scale (SGS) model and the center discrete format are closer to the experimental results, and the density of the grid around the cylinder affects the length of the recirculation. Zhang et al.[7]use the large eddy simulation (LES) to obtain the flow past a finite circular cylinder with a height-to-diameter ratio of 1.5 and an infinite circular cylinder of the same diameter at a Reynolds number Re =3900. Ali and Sheldon[8]investigated the effects of Reynolds numbers and spacing ratios on the flow characteristics and the hydrodynamic forces on the two side-by-side arranged cylinders of the same diameter. Cross-flows arou-nd two, three and four circular cylinders in tandem, side-by-side, isosceles triangle and square arrangements are simulated using the incompressible lattice Boltzmann method with a second-order accurate curved boundary condition[9]. Vedat et al.[10]found that the asymmetric flow behavior of two side-side circular cylinders downstream can be suppressed with a splitter plate in a shallow water. Zeng et al.[11]examine the water wave radiation by arrays of truncated circular cylinders. Based on the eigenfunction expansion and Graf’s addition theorem for Bessel functions, an analytical method that includes the effects of evanescent modes is developed to analyze such arrays of cylinders. With respect to the turbulent signal analysis, Huang and Lu[12]analyzed the velocity signal at a point behind the cylinder, using the EMD method at Re =152. The large energy-containing modes were found to have a clear physical meaning, and an obvious intra-wave frequency modulation was found at the corresponding instantaneous frequency.

At present, the flows around two side-by-side circular cylinders of different diameters were not well studied. Dalton et al.[13]and Zhao et al.[14]found that the vortex street exists behind the cylinders only at very small spacing ratios for the two cylinders. Dalton et al.[13]showed that both the drag and the lift coefficients of the main cylinder were reduced because of the existence of a small cylinder. Zhao et al.[14]simulated the flow around two side-by-side circular cylinders at Re =500 and at the diameter ratio of 0.25. It was found that the spacing ratio has little effect on the mean drag coefficient of the small cylinder, while has a great influence on the wake of the main cylinder and the mean drag and lift coefficients. Yang et al.[15]showed the effects of the piggyback cylinder on the drag and lift coefficients of the main cylinder in an oscillatory flow.

In the present work, the flow around two side-byside circular cylinders of different diameters is investigated numerically by the LES method, based on the dynamic Smagorinsky SGS model. and the EMD method is used to analyze the suppression mechanism of the vortex shedding. The primary coverage is focused on the effects of the two side-by-side cylinders of different diameters on the vortex shedding behind two cylinders and the force on the main cylinder.

1. Computational details

1.1 Governing equation and numerical method

The basic idea of the LES is to calculate large scale eddies directly by solving the filtered Navier-Stokes equations, and to simulate the small scale eddies by a SGS model. The governing equations used for the LES in this paper are as follows:

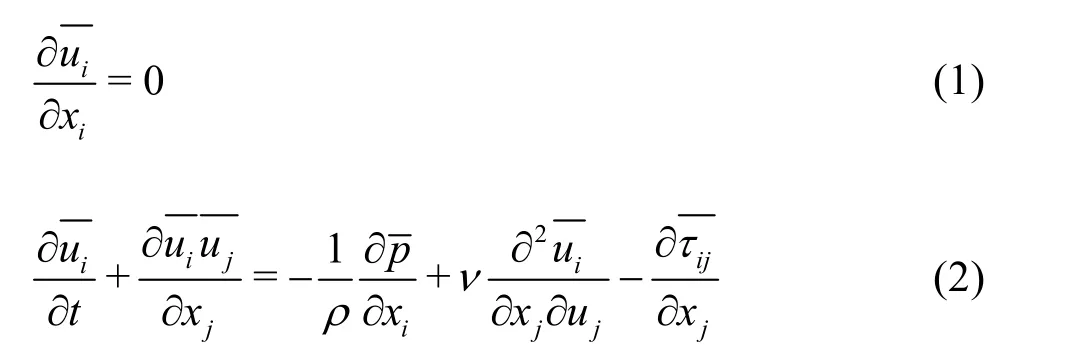
whereuiand ujare the filtered mean velocity components,p is the mean pressure, r is the water density, n is the kinematic viscosity of the water,tijdenotes the mean SGS stress resulting from the filtering operation, which is unknown and is modeled as

where tkkis incorporated in the pressure, resulting in a modified pressure term, ntis the SGS kinematic viscosity, Sijis the rate-of-strain tensor, and can be modeled as

The most basic SGS model was built by Smagorinsky and then further developed by Lilly. In the Smagorinsky-Lilly model, the sub-grid kinematic viscositytn is modeled by

where Lsis the mixing length for the SGS, andcan be computed by

where k=0.42is the von Karman constant, y is the distance to the nearest wall, D is the volume of the computational cell. CSis the Smagorinsky constant. Good results for a wide range flows were obtained when the Smagorinsky constant CS=0.1-0.14[16]. All computations in this paper are carried with CS=0.1.

In the present simulation, the finite volume method (FVM) applied on the structured grids is used to discrete the unsteady Navier-Stokers equations, the SIMPLE algorithm is used for the pressure-velocity coupling between the momentum and continuity equations, the bounded central differencing is used for themomentum discretization and the dynamic Smagorinsky-Lilly model is used in the SGS models.

1.2 Validation of numerical model

To validate the numerical model, the 3-D turbulent flow around a single circular cylinder is simulated at a sub-critical Reynolds number (R e =3900), where U0is the free stream velocity and U is the mean velocity. The size of the whole computational domain is 35 D ´ 20D ´pD , and D is the diameter of the cylinder. Distribution of the mean streamwise velocity along the centerline of the cylinder is shown in Fig.1, which agrees well with the experimental results of Jia and Liu[17]. Figure 2 shows the relationship between the pressure coefficient (Cp) at a point of the cylinder surface and the corresponding central angle (q) , where q is the angle in the clockwise direction, starting from the centerline along the streamwise direction. Figure 2 shows that the simulated results agree well with the experimental results of Jia and Liu[17]. Therefore, the reliability of the numerical model and method is validated by numerically studying the flow around the single cylinder.

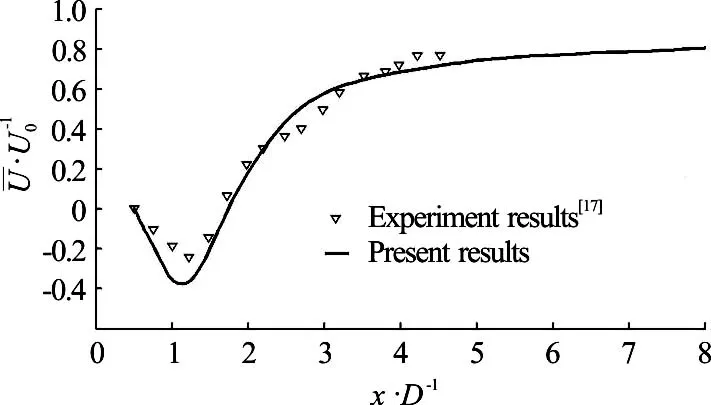
Fig.1 Distribution of mean steamwise velocity along the centerline of the cylinder

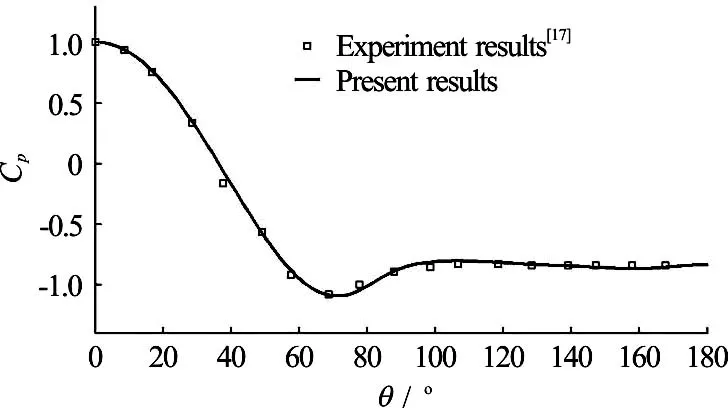
Fig.2 Pressure coefficient pC on the surface of the cylinder

1.3 Computational model and grid generation

The geometric size of the computational domain and the boundary conditions imposed for the flow around the two side-by-side circular cylinders of different diameters are shown in Fig.3. The size of the whole computational domain is 35 D ´ 20 D´ 4D with the main cylinder diameter (D) being 0.01 m and the small cylinder diameter (d) being 0.005 m. The bottom center of the main cylinder is chosen as the origin of the coordinates, and X axis, Y axis and Z axis are as shown in Fig.3. If the distance between the two cylinder centers is denoted as T, four working cases are analyzed in this paper with / =T D 1.2, 1.5, 1.8, 2.7. The inlet velocity is 0.39 m/s and the turbulence intensity is 5%. The two cylinder surfaces are defined as no-lip walls with no roughness, and other boundary conditions are shown in Fig.3. In the four working cases, the value of+y of the main cylinder is less than 0.55 and that of the small cylinder is less than 0.7, which are well within the requirement of the LES. Figure 4 shows the symmetrical surface mesh and the local mesh near the two cylinder surfaces.

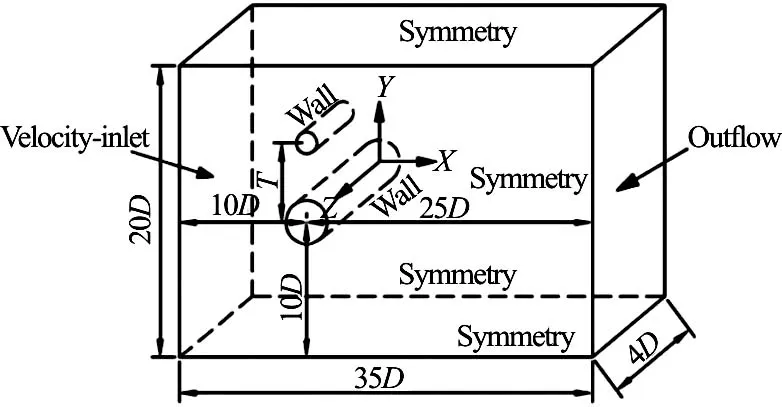
Fig.3 Computational domain

Fig.4 Mesh on symmetric surface

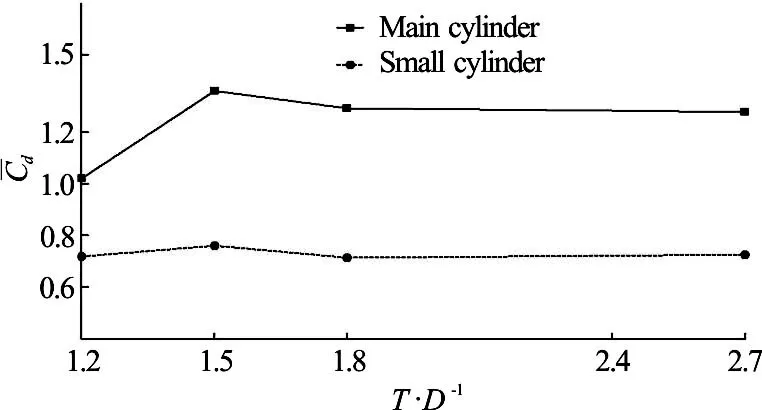
Fig.5 Effects of spacing ratios on mean drag coefficient of the two cylinders

2. Results and discussions

2.1 Hydrodynamic characteristics and turbulent characteristics

Figure 5 shows the effects of spacing ratios on the mean drag coefficients(Cd) of the two cylinders.With the increase of T /D, the mean drag coefficient of the main cylinder increases at first, and then decreases, and gradually tends to a stable value. The drag coefficient of the main cylinder is smaller than those in other three cases when T / D =1.2, while it is larger when T / D =1.5. It is due to the fact that the vortex shedding of the main cylinder can be strongly suppressed by the small cylinder when T /D =1.2 and improved when T /D =1.5. With the increase of T /D, the effect of the small cylinder on the main cylinder gets smaller and smaller. In addition, T /D has little effect on the mean drag coefficient of the small cylinder.

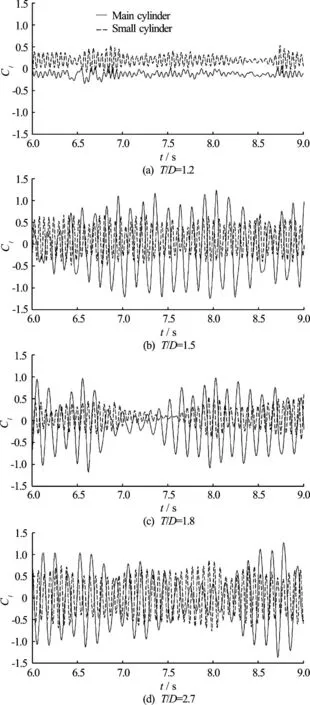
Fig.6 Lift coefficient curves of the two cylinders at different values of /T D

Figure 6 shows the evolution of the lift coefficient (Cl) curves of the two cylinders at different values of T /D. It can be seen from Fig.6 that the lift coefficients of the two cylinders oscillate irregularly. It shows that remarkable 3-D turbulence characteristics exists in the flow around the two cylinders at a sub-critical Reynolds number (R e =3900). The fluctuating range of Clof the main cylinder is smaller than those in the other three cases when T / D =1.2, while it is larger when T / D =1.5. It is also due to the fact that the vortex shedding of the main cylinder can be strongly suppressed by the small cylinder when T / D =1.2 and improved when T /D =1.5.

Fig.7 (Color online) Effects of spacing ratios on vorticity

This is further confirmed by examining the vorticity contours behind the two cylinders as shown in Fig.7. The biased flow is characterized by a gap flow biased towards one of the two cylinders. In Fig.7 oneclearly sees the biased flow with the gap flow biasing towards the small cylinder when T / D =1.2. And the biased flow disappears when T / D =1.5. With the increase of T /D, the interactions between the two shedding processes become weaker andweaker and the sheddings behind the two cylinders become relatively independent. This is called parallel vortex streets.

Fourier analyses of the lift coefficients of the two cylinders are carried out for various spacing ratios. The dominant frequency of the lift coefficient can be regarded as the vortex shedding frequency. The inset in Fig.8(a) shows the corresponding magnification of the power spectra of the fluctuating lift at T / D =1.2.

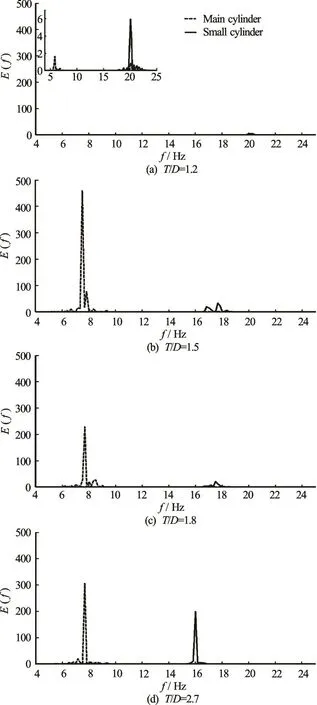
Fig.8 Power spectrum (())Ef of the lift forces of two cylinders of different /T D

Figure 8 shows that when T /D =1.2, there are two dominant sharp peak frequencies for the main cylinder and the amplitude of the lift coefficient is quite small. The larger vortex shedding frequency is equal to the vortex shedding frequency of the small cylinder. It is shown that the flow biases frequently towards the small cylinder. When T / D =1.5, the vortex shedding of the main cylinder speeds up, the dominant sharp peak frequency for the main cylinder becomes smaller and the amplitude of the lift coefficient is larger than those in other three cases. Strong cyclical characteristics are seen in the vortex shedding of the main cylinder when T / D =1.5. And the vortex shedding frequencies of the two cylinders tend to be stable with the increase of T /D.

Figure 9 shows the distribution of the mean velocity along the central axis of the main cylinder for different values of T /D. The recirculation length (Lr) represents the length of the central axis when U is less thanUminand it symbolizes the distance between the center of the initial vortex formed behind the cylinder and the center of the cylinder. For the main cylinder, when T / D =1.2, Lris larger while the mean drag coefficient is smaller than those in other three cases. When T /D =1.5, the recirculation length is smaller while the mean drag coefficient is larger than those in other three cases.

Fig.9 Mean velocity along the central axis of the main cylinder

Figure 10 shows the evolution of the Reynolds stressin the near wake with different values of T /D. X /D is the distance between the location in the near wake and the center of the cylinder. With the increase of X /D in the near wake, the Reynolds stress of the main cylinder increases gradually when T / D =1.2. However, in other three cases, the Reynolds stress of the main cylinder increases at first, and then decreases and the vortex shedding begins at the location of T / D =1.5 in the near wake. In conclusion, the spacing ratio has a great effect on the turbulence characteristics of the main cylinder.

2.2 EMD and coherent structure

The empirical mode decomposition (EMD) is toadaptively decompose the original signal into a sum of some different intrinsic mode function (IMF) components. The IMFs need to satisfy the following two conditions[18]: (1) In the whole data series, the number of the extremes (the maxima and the minima) and the number of zero crossings must be equal, or differ at most by one. (2)The mean value of the envelopes defined by the local maxima and minima must be zero at any point.

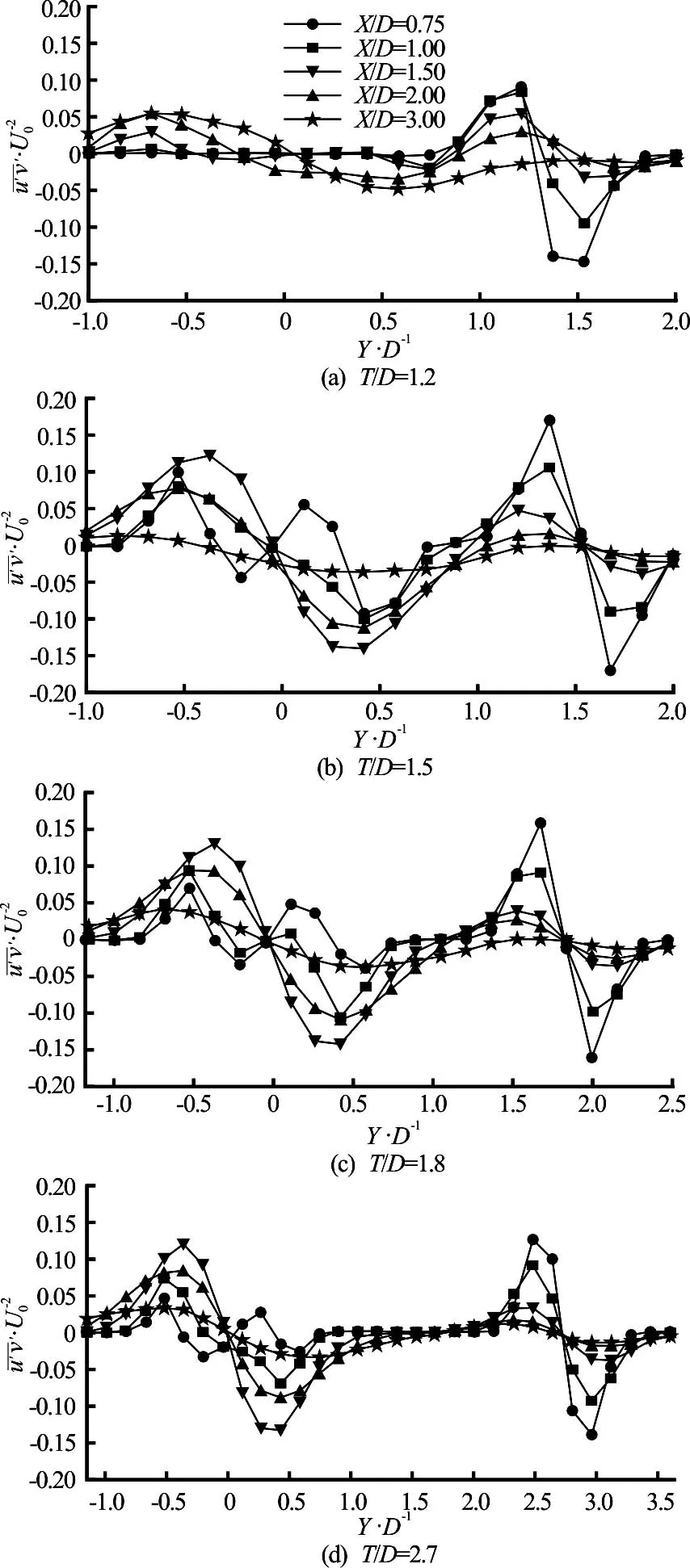
Fig.10 Evolution of Reynolds stress in the near wake with different values of /T D

Huang et al.[18]suggested implementing a shift process to get the IMFs from the original signal ()xt. The original signal ()xt can be expressed by

where rn(t) is the number of the IMFs, rn(t) is the final residue, which is the main trend of x(t), and hi(t) (i =1,2,L ,n) are the IMFs, which are nearly orthogonal to each other.

As we all know, when /T D is equal to 1.2, the vortex shedding of the main cylinder is strongly suppressed by the small cylinder and the drag and lift coefficients of the main cylinder are smaller than those in other three cases. In order to further study the wake vortex turbulence characteristics of the main cylinder, the EMD method is used to analyze the vertical velocity of the point ( X / D =3, Y/ D =0,Z /D =2).

Figure 11 shows different modes of the vertical velocity signal decomposed through the EMD method. Figure 11(a) shows that the time scale changes from the small scale to the large scale with the increase of the modes, and the time scale of the first mode is smaller than those of other modes. From Fig.11(b), we can see that the smaller scale has a stronger intermittency. The probability density function (PDF) of most modes deviates from the Gaussian distribution, as shown in Fig.11(c), which is due to the fact that the turbulent flow itself is structured.

Figure 12 illustrates the estimated mean frequency f(m) versus the mode index m, in which the inset shows the corresponding mean periodT(m) versus the mode index m. It is shown that there is a linear relationship between the mean period and the mode of the formf(m )= Ae-bmwith A =35, b= 0.714 in the semi-log coordinates. Figure 13 shows the distribution of the mean energy of the IMFs.

As we all know, the turbulence is dominated by a coherent structure, which can be recognized by the mean energy. If the mean energy in the mode exceeds 10% of the whole fluctuation energy, the mode is defined as the coherent mode.

Table 1 and Table 2 show the mean energy and its corresponding mean period of different modes of the vertical velocity at T/ D =1.2 and T /D =1.5. From Table 1, we can see, for the vertical velocity at T / D =1.2, there are two modes (Modes 2 and 3) with the mean energy over 10%. The amount of the energy contained in these two modes accounts for 89% of the total energy. Their mean periods are 0.1642 s and 0.2090 s, respectively. Table 2 shows that, for the vertical velocity at T /D =1.5, there are three modes (Modes 1, 2 and 3) with the mean energy over 10%. The amount of the energy contained in these three mode s accoun ts fo r 96.09% o f the to ta l ene rgy. The ir meanperiodsare0.1158s,0.1422sand0.2293s,respectively. When T/D =1.2 and T /D =1.5, the average periods of the restructured coherent structure are 0.1656 s and 0.1286 s, respectively. And the vortex shedding periods of the main cylinder are 0.1712 s and 0.1364 s, as obtained by the LES. The vortex shedding period of the single circular cylinder is about 0.140 s. It is found that the vortex shedding period of the main cylinder is consistent with the period of the restructured coherent structure. The analysis with the EMD method shows that when T /D =1.2, the vortex shedding of the main cylinder is strongly suppressed by the small cylinder, however, the vortex shedding of the main cylinder is improved slightly when T / D= 1.5.

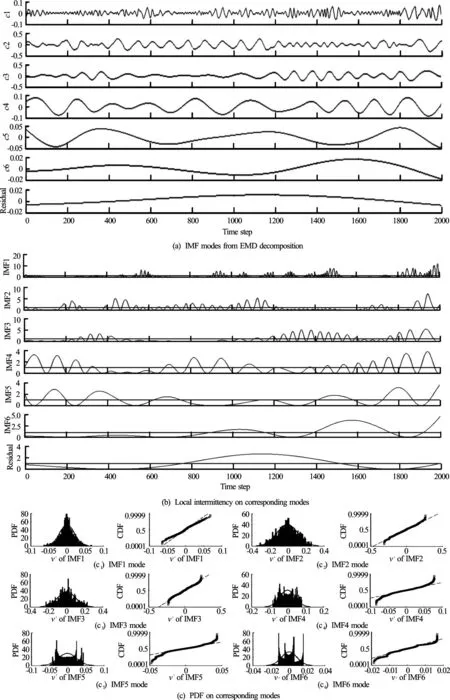
Fig.11 EMD analysis on the instantaneous vertical velocity of point at T/D =1.2

Fig.12 Mean frequency and mean period of IMF

Fig.13 Mean energy of IMF

Table 1 Mean energy and mean periods of different modes at T/D =1.2

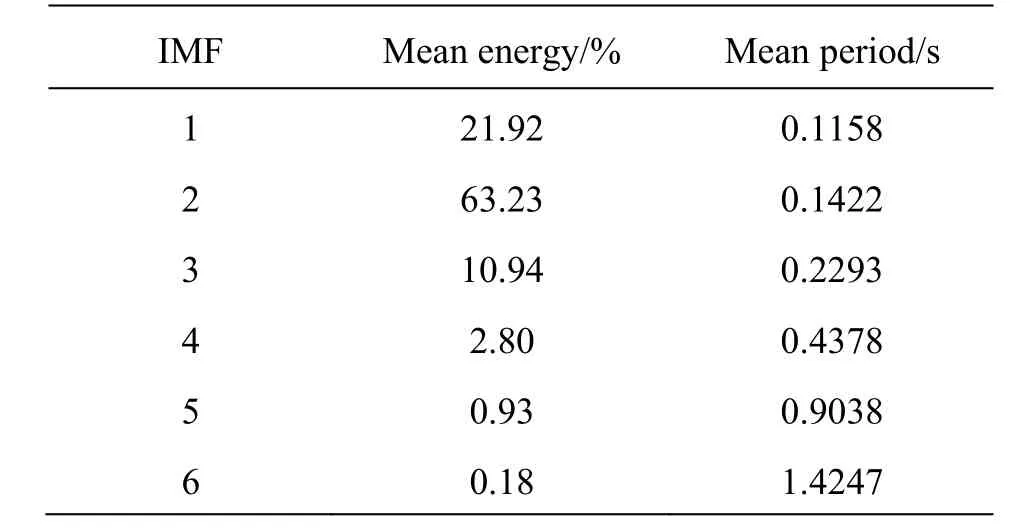
Table 2 Mean energy and mean periods of different modes at T/D =1.5

3. Conclusions

In this paper, we study the effect of the /T D values on the drag and lift coefficients, the vortex shedding frequency, the coherent structure and the turbulence characteristics in the wake behind the two cylinders. The relationship between the period of the vortex shedding and the force on the main cylinder is analyzed using the EMD method.

The drag and lift coefficients of the main cylinder are smaller than those in other three cases when T/ D =1.2, while they are larger than those in other three cases when T /D =1.5.

The biased flow can be observed with the gap flow biasing towards the small cylinder when T / D= 1.2. And the biased flow disappears when T /D =1.5. The vortex shedding of the main cylinder is strongly suppressed by the small cylinder when T / D =1.2 and improved when T / D =1.5. The vortex shedding frequencies of the two cylinders tend to be stable with the increase of the T /D values.

The recirculation length is larger while the mean drag and lift coefficients are smaller than those in other three cases when T / D =1.2. However, the recirculation length is smaller while the mean drag and lift coefficients are larger than those in other three cases when T / D =1.5. When T /D =1.5, 1.8, 2.7, the vortex shedding begins to appear at the location of X/D =1.5 in the near wake.

There is a linear relationship between the mean period and the mode in the semi-log coordinates. The vortex shedding period of the main cylinder is consistent with the period of the restructured coherent structures quantitatively.

[1] Wang Z., Zhou Y., Li H. Flow-visualization of a two sideby-side cylinder wake [J]. Journal of Flow Visualization and Image Processing, 2002, 9(2-3): 123-138.

[2] Sumner D. Two circular cylinders in cross-flow: A review [J]. Journal of Fluids and Structures, 2010, 26(6): 849-899.

[3] Xu S. J., Zhou Y., So R. M. C. Reynolds number effects on the flow structure behind two side-by-side cylinders [J]. Physics of Fluids, 2003, 15(5): 1214-1219.

[4] Alam M. M., Moriya M., Sakamoto H. Aerodynamic characteristics of two side-by-side circular cylinders and app-lication of wavelet analysis on the switching phenomenon [J]. Journal of Fluids and Structures, 2003, 18(3-4): 325-346.

[5] Alam M. M., Zhou Y. Flow around two side-by-side closely spaced circular cylinders [J]. Journal of Fluids and Structures, 2007, 23(5): 799-805.

[6] Kravchenko A. G., Moin P. Numerical studies of flow over a circular cylinder at ReD=3900 [J]. Physics of Fluids, 2000, 12(2): 403-417.

[7] Zhang H., Yang J. M., Xiao L. F. et al. Large-eddy simulation of the flow past both finite and infinite circular cylinders at Re =3900 [J]. Journal of Hydrodynamics, 2015, 27(2): 195-230.

[8] Ali V., Sheldon I. G. Two-dimensional side-by-side circular cylinders at moderate Reynolds numbers [J]. Computers and Fluids, 2011, 51(1): 136-144.

[9] Kang X. Y., Su Y. P. Lattice Boltzmann simulation of flow around two, three and four circular cylinders in close proximity [J]. Science China Physics, Mechanics and Astronomy, 2012, 55(10): 1873-1885.

[10] Vedat O., Akar M. A., Akilli H. et al. Suppression of asymmetric flow behavior downstream of two side-byside circular cylinders with a splitter plate in shallow water [J]. Measurement, 2013, 46(1): 442-455.

[11] Zeng X. H., Shi M., Huang S. L. Hydrodynamic interactions of water waves with a group of independently oscillating truncated circular cylinders [J]. Acta Mechanica Sinica, 2016, 32(5): 773-791.

[12] Huang Y. X., Lu Z. Application of Hilbert-Huang transform in analysis of Duffing equation and wake flow over a cylinder [J]. Chinese Quarterly of Mechanics, 2005, 26(4): 658-663.

[13] Dalton C., Xu Y., Owen J. C. The suppression of lift on a circular cylinder due to vortex shedding at moderate Reynolds number [J]. Journal of Fluid Structure, 2001, 15(3-4): 617-628.

[14] Zhao M., Cheng L.,Teng B. et al. Hydrodynamic forces on dual cylinders of different diameters in steady currents [J]. Journal of Fluids and Structures, 2007, 23(1): 59-83.

[15] Yang K., Cheng L., An H. et al. The effect of a piggyback cylinder on the flow characteristics in oscillatory flow [J]. Ocean Engineering, 2013, 62: 45-55.

[16] Zhao W., Huhe A. Large-eddy simulation of three-dimensional turbulent flow around a circular pier [J]. Journal of Hydrodynamics, Ser. B, 2006, 18(6): 765-772.

[17] Jia X. H., Liu H. Large eddy simulation of flow around two circular cylinders [J]. Chinese Journal of Hydrodynamics, 2008, 23(6): 625-632(in Chinese).

[18] Huang Y., Schmitt F. G., Lu Z. et al. Analysis of daily river flow fluctuations using empirical mode decomposition and arbitrary order Hilbert spectral analysis [J]. Journal of Hydrology, 2009, 373(1-2): 101-111.

10.1016/S1001-6058(16)60758-8

May 4, 2015, Revised March 28, 2016)

* Project supported by the National Natural Science Foundation of China (Grant Nos. 11572203, 11332006), the Innovation Program of Shanghai Municipal Education Commission (Grant No.13YZ124).

Biography:Xiang Qiu (1978-), Male, Ph. D., Professor