Shedding frequency of sheet cavitation around axisymmetric body at small angles of attack*

Chu-rui Wan (万初瑞), Hua Liu (刘桦),2

1. MOE Key Laboratory of Hydrodynamics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: jsvan@139.com

2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration Shanghai 200240, China

Shedding frequency of sheet cavitation around axisymmetric body at small angles of attack*

Chu-rui Wan (万初瑞)1, Hua Liu (刘桦)1,2

1. MOE Key Laboratory of Hydrodynamics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China, E-mail: jsvan@139.com

2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration Shanghai 200240, China

2017,29(3):520-523

Cavity shedding of cavitating flows around an axisymmetric body belongs to the unsteady cavitating flows in the condition of steady incoming current. The periodic characteristics of unsteady cavitating flows around an axisymmetric body at small angles of attack are investigated experimentally and numerically. The evolution and shedding process of the three-dimensional sheet cavitation are computed numerically by the Reynolds averaged Navier-Stokes equations and the RNG -ke model. The modification approach for eddy viscosity coefficient in the transition area of the two-phase flow is adopted to reproduce the shedding process of cavitating flows. The computed frequency of the cavity shedding coincides with the experimental data for the cases of unsteady cavitating flows around axisymmetric bodies with four headforms. Given the cavitation number, the shedding process of the cavitating flow depends heavily on the headform of the axisymmetric body. If the angle of attack of the axisymmetric body is greater than a critical value, the violent shedding of the sheet cavitation seems to be depressed.

Cavitating flow, shedding, fluctuation, axisymmetric headform

Unsteady behavior of cavitation on two-dimensional hydrofoils in the case of steady incoming flows has been the subject of intensive investigations. The Strouhal number for the lift and the drag fluctuation, defined by the chord length, was obtained experimentally as 0.14 for an Eppler foil[1]. Using the high speed photography, the evolution and abrupt cavity separation of unsteady cavitation on a hydrofoil NACA4412 were analyzed and the Strouhal number, corresponding to the violent deformation of the cavity, was proposed as 0.158[2]. Through numerical simulation, it was found that, for the unsteady cavitating flow on twodimensional hydrofoils NACA0015, the computedvalue of the Strouhal number is equal to 0.1[3].

Regarding the cavitation pattern on an axisymmetric body with different headforms, it can be divided into cavitation inception, developed cavitation and supercavitaion. There are several experimental investigations on the mechanism of unsteady cavitating flows through analyzing the cavity profile measured by high speed photography. It turns out that the reentrant jet moving through the cavity would be the major factor causing the cavity to detach from the front near the cavitator leading edge[4]. Such periodic fluctuation of the cavity profile affects hydrodynamic lift and drag on the headform[5]. In order to model the fluctuating hydrodynamic loads, it is essential to establish an empirical formula to calculate the frequency of unsteady cavitating flows.

An experimental investigation on unsteady cavitating flows on an axisymmetric headform was carried out at SSRI K15 Cavitation Tunnel[6]. The characteristics of the frequency of cavity evolution and hydrodynamic loads were discussed based on the high speed movies and the wavelet analysis of the measured time series of forces. The length of the test section is 2.6 m,its cross section is a square of 0.6 m by 0.6 m. The maximum flow speed reaches 12 m/s and the minimum static pressure can be controlled from near vacuum to 200 kPa. A de-aeration system was used to control the dissolved air content of the water. The relative dissolved air content is around 0.3 in the experiments measured by a Van Slyke equipment. The cavity profiles were recorded by the high speed photograph HIGHSPEED10-16. The recording rate was 6 000 frame per second. A three component balance was adopted to measure the lift, drag and moment acting on a slender model with different headforms. We selected four headforms in the experiment, including an elliptic headform, a 1/4-caliber give headform, a 600-conical headform and a hemispheric headform, shown in Fig.1. The heaform diameter is 62.9 mm. The axisymmetric model consisted of a headform and a parallel cylinder with the length of 657 mm. The strut-mounted slender model was attached to the wall of the test section of the cavitation tunnel.

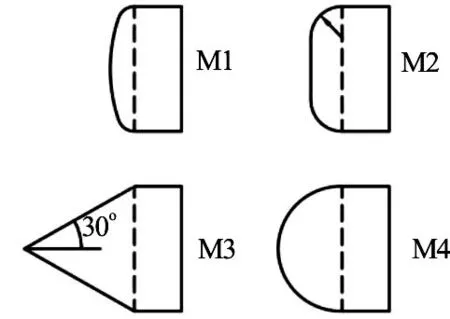
Fig.1 Four headforms used in experiments

The cavitation number s is defined as

where p¥and V¥are the pressure and reference velocity, respectively, p is the vapor pressure at the bulk temperature of the water, and r is the water density.

The Strouhal number St is defined as

where f stands for the fluctuating frequency of unsteady cavitating flows and D represents the diameter of the headform.

Analyzing the time series of the drag acting on the headforms by FFT and the images of cavity by digitalizing high speed records, the measured frequencies of the cavity evolution are shown in Table 1. The averaged value of the Strouhal number obtained by analyzing the measured drag on the models is equal to 0.107. Here, we might propose an empirical formula St =0.107 ± 0.014 of the periodic shedding of the cavitation flows around an axisymmetric body with different headforms and small angle of attack.

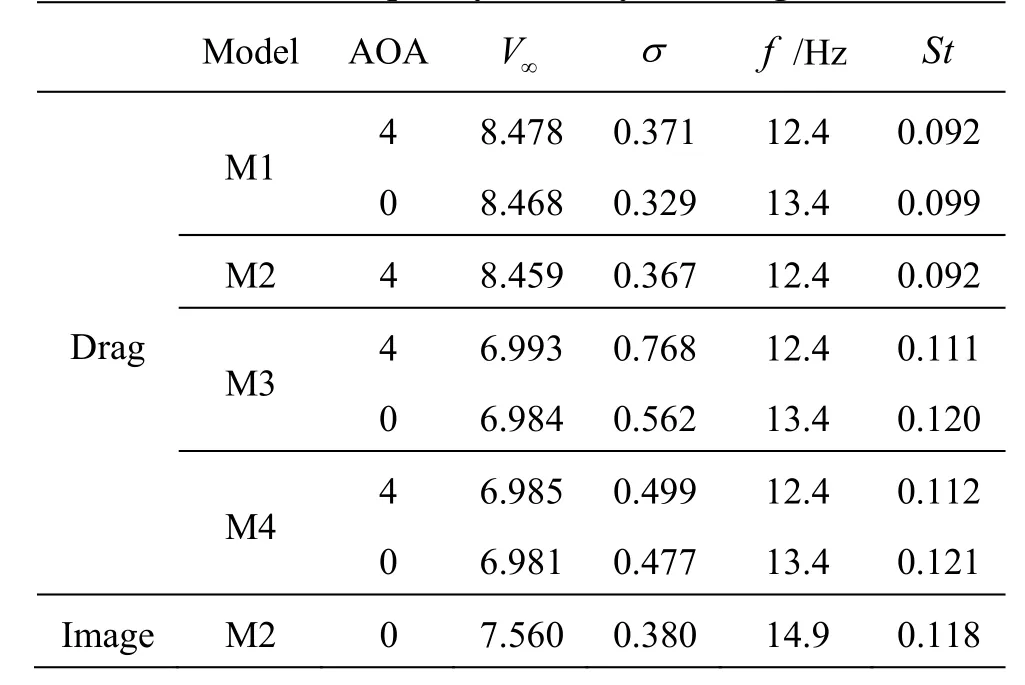
Table1 Measured frequency of cavity shedding

We carried out numerical simulations of unsteady cavitating flows around the axisymmetric body with four headforms. The RANS equations and the RNG k-e model are used to simulate the cavitating turbulent flows[7,8]. The cavitation model developed by Single et al. was adopted in the present study[9]. The grid convergence was checked carefully in terms of the pressure distribution on the axisymmetric body. The grid number of the meshes for the numerical simulations is 1.67M and the corresponding+=30-60 y . In order to reproduce the shedding process of the cavitating flow around an axisymmetric body at small angles of attack, the modification approach of decreasing the vortex viscosity of two phase flow inside the cavitation region is implemented in numerical simulations[10].

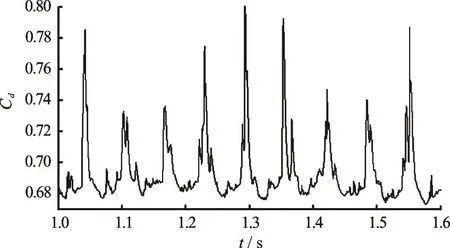
Fig.2 Time series of drag force on cavitating model M2

For the model M2, the computed time series of the drag acting on the axisymmetric body is plotted in Fig.2 for the case of s=0.38and zero angle of attack. Analyzing the drag by FFT, the peak frequency of the spectra is equal to 15.6 Hz and the corresponding Strouhal num ber is 0.12 4. It is co nfirmed by the ex perimentaldataasshowninTable1.Thesnapshotsofthe shedding process of unsteady cavitating flows are shown in Fig.3 for the case of zero angle of attack and in Fig.4 for the case of a small angle of attack. It can be seen that the violent detachment near the separating point of the cavity on the axisymmetric body appear with three-dimensional cavities.

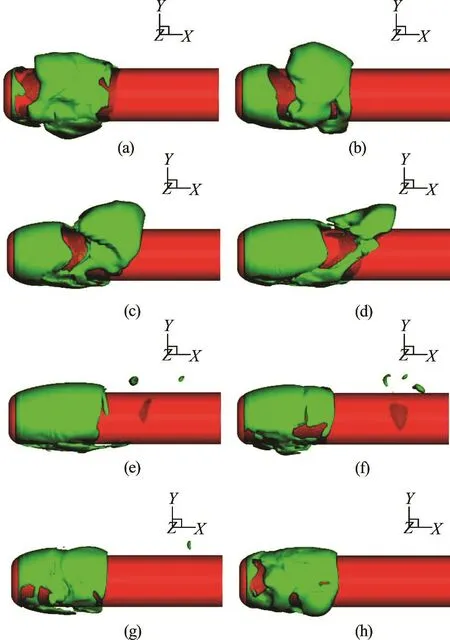
Fig.3 (Color online) Snapshots of cavity shedding process for M2 with 0oAOA. The fluctuation period T =0.064s. Time interval is 1/8 of the fluctuation period

Figure 5 presents the pressure distribution on the surface of the axisymmetric body in which the panels corresponds to the subfigures of Fig.4. During the process of shedding of the sheet cavitation and developing of the cloud cavitation, significant variations of the pressure distribution on the body appear particularly at the lee side of the body at small angles of attack.

The computed time series of the drag on the model at small angles of attack are shown in Fig.6. Comparing the computed drag for the cases of smaller angle of attack, it turns out that the fluctuation peaks appear at almost the same time and, however, for the case of the angle of attack is equal too8, the computed drag is significantly different from those at smaller angles of attack. As the angle of attack is higher than a critical value, the violent shedding of the sheet cavitation seems to be depressed.

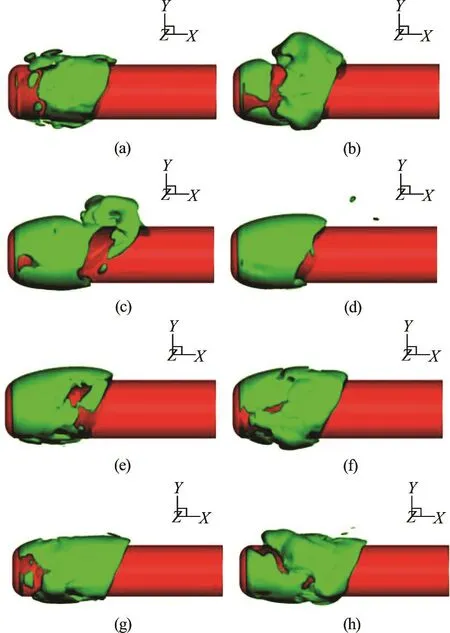
Fig.4 (Color online) Snapshots of cavity shedding process for M2 at 2oAOA. The fluctuation period T =0.074s . Time interval is 1/8 of the fluctuation period

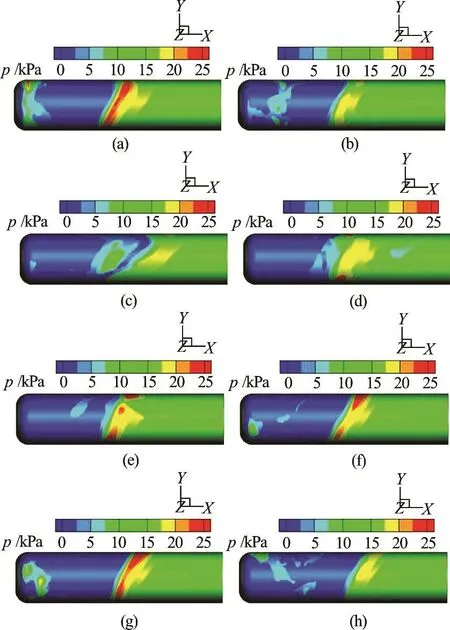
Fig.5 (Color online) Pressure distribution on the surface of a cavitating axisymmetric body. The panels correspond to those of Fig.4

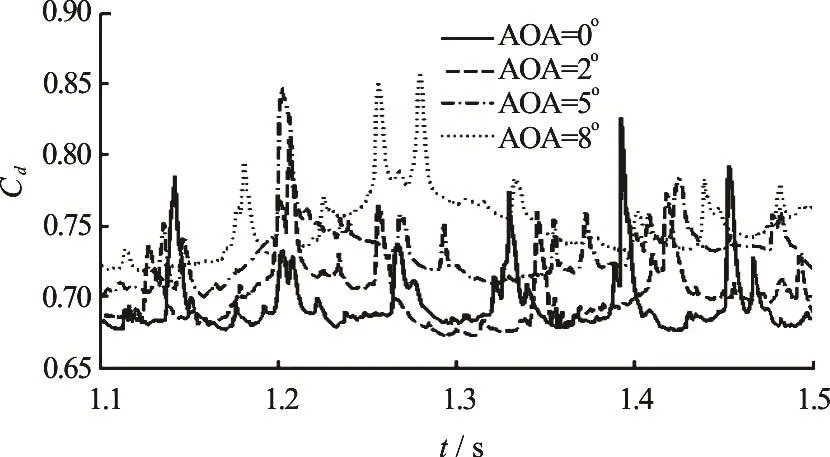
Fig.6 Time series of the drag force on the axisymmetric body with different angles of attack

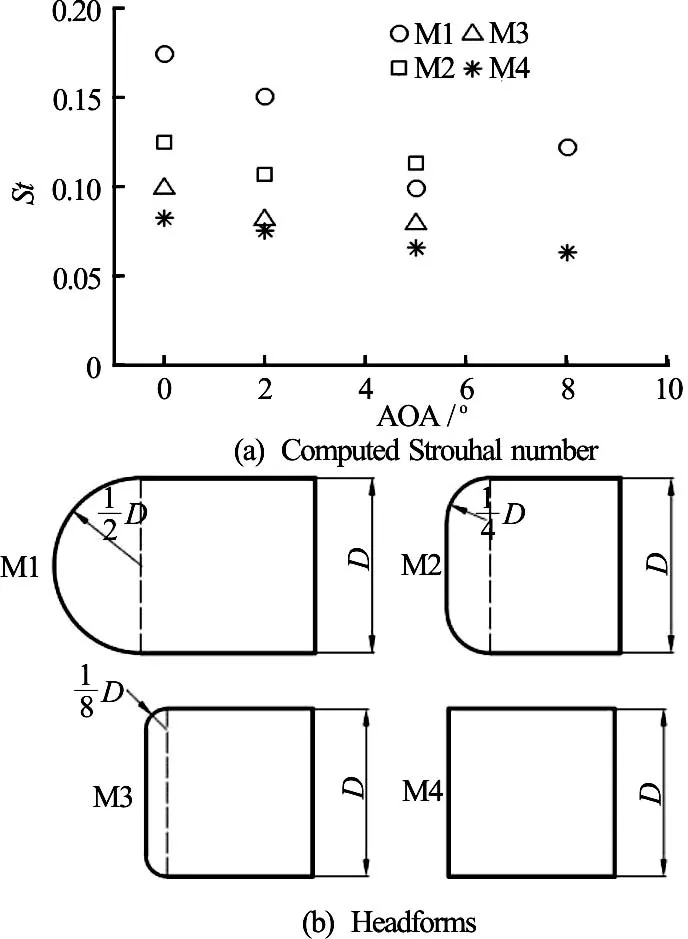
Fig.7 The relationship between Strouhal number and the angle of attack of an axisymmetric body with different headforms

Carrying out a series of numerical experiments, we can obtain the relationship between the frequency characteristics and the angle of attack for the axisymmetric body with different headforms. As shown in Fig.7, it is interesting to note that, for a given headform, the Strouhal number of the shedding sheet cavity is inversely proportional to the angle of attack, and, for a given angle of attack, the Strouhal number becomes greater from the blunt headform to the hemispheric headform.

As a summary, the shedding process of unsteady cavitating flows and the corresponding hydrodynamic loads are studied experimentally and numerically for an axisymmetric body with four blunt headforms at small angles of attack. Based on the measured time series of drag and high speed image of cavity, the Strouhal number of low frequency fluctuation of the violent shedding sheet cavitation can be estimated by St =0.107 ± 0.014 for different headforms. It turns out that, for a given headform, the Strouhal number of the violent shedding of the unsteady cavitating flows around an axisymmetric body decreases as the angle of attack increases. The violent shedding will be depressed as long as the angle of attack is greater than a critical value. To understand the mechanism of rapid changes of the pressure distribution on the surface of a cavitating axisymmetric body, more effort should be made in measuring the flow field inside the unsteady cavitating flows with violent shedding of cavity[11,12]and developing the corresponding numerical simulation approaches[13,14].

[1] Sakagami K., Kuwako H., Ito Y. et al. Behavior of the lift and the drag fluctuations on a foil in cavitation violent vibration [J]. Proc. of Japanese Society of Mechanical Engineers (B), 1990, 56(525): 1223-1229.

[2] He Y. S., Liu H., Zhao G. A study on pulsation of twodimensional cavitating flow [J]. Acta Mechanica Sinica, 1997, 29(1): 1-7(in Chinese).

[3] Arndt R. E. A., Song C. C. S. et al. Instability of Partial cavitation: A numerical/experimental approach [C]. The 23rd Symposium on Naval Hydrodynamics. Rouen, France, 2000.

[4] Stinebring D. R., Billet M. L., Lindau J. W. Developed cavitation-cavity dynamics [R]. RTO EN-010, Brussels, Belgium: The von Kármán Institute (VKI), 2001.

[5] Gnanaskandan A., Mahesh K. Numerical investigation of near-wake characteristics of cavitating flow over a circular cylinder [J]. Journal of Fluid Mechanics, 2017, 790: 453-491.

[6] Liu H., He Y. S., Zhao G. A study on pulsation of axisymmetric cavitating flow [J]. Shanghai Journal of Mechanics, 1997, 18(2): 99-105(in Chinese).

[7] Coutier-Delgosha O., Fortes-Patella R., Reboud J. L. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation [J]. Journal of Fluids Engineering, 2003, 125(1): 38-45.

[8] Orszag S. A., Yakhot V., Flannery W. S. et al. Renormalization group modeling and turbulence simulations [J]. Near-wall Turbulent Flows, 1993, 1031-1046.

[9] Singhal A. K., Athavale M. M., Li H. et al. Mathematical basis and validation of the full cavitation model [J]. Journal of Fluids Engineering, 2002, 124(3): 617-624.

[10] Wang Y. Y., Wang B. L., Liu H. Numerical simulation of sheet cavity shedding and cloud cavitation on a 2D hydrofoil [J]. Chinese Journal of Hydrodynamics, 2014, 29(2): 175-182(in Chinese).

[11] Wan C., Wang B., Wang Q. et al. Probing and imaging of vapor–water mixture properties inside partial/cloud cavitating flows [J]. Journal of Fluids Engineering, 2017, 139: 031303-1.

[12] Hu C. L., Wang G. Y., Huang B. et al. The inception cavitating flows over an axisymmetric body with a blunt headform [J]. Journal of Hydrodynamics, 2015, 27(3): 359-366.

[13] Ma J. S., Hsiao C. T., Chahine G. L. A physics based multiscale modeling of cavitating flows [J]. Computers and Fluids, 2017, 145: 68-84.

[14] Chen Y., Chen X., Li J. et al. Large eddy simulation and investigation on the flow structure of the cascading cavitation shedding regime around 3D twisted hydrofoil [J]. Ocean Engineering, 2017, 129: 1-19.

10.1016/S1001-6058(16)60764-3

March 10, 2017, Revised April 11, 2017)

* Project supported by the National Natural Science Foundation of China (Grant Nos. 10972138, 11632012), the National Key Basic Research Development Program of China (973 Program, Grant No. 2013CB036102).

Biography:Chu-rui Wan (1985-), Male, Ph. D. Candidate

Hua Liu, E-mail: hliu@sjtu.edu.cn