轴承对轮胎动平衡机动态特性影响的研究

马建峰，张蕴泽，李超

轴承对轮胎动平衡机动态特性影响的研究

马建峰1，张蕴泽2，李超1

（1.北京工业大学机械工程及应用电子技术学院，北京100124；2.哈尔滨工业大学附属中学，黑龙江哈尔滨150086）

针对轮胎动平衡机设计当中建模精度的问题，对某轮胎动平衡机进行三维实体建模并简化，并将模型导入ANSYS中进行模态分析。对含轴承和不含轴承的模型进行分析对比，发现建模中轴承对系统动态特性分析精度影响很大，同时进行了实验验证，有限元仿真和实验结果两者具有较好的一致性，说明模型建立正确。在轮胎动平衡机设计环节，轴承的影响必须考虑。

动平衡机；轴承；模态分析；激振

近年来，我国在轮胎动平衡机研制方面发展迅速，但在系统稳定性、精度等方面，与国外同类产品相比，还存在较大的差距。随着轮胎厂对轮胎精度和可靠性需求的增加，动平衡机的行业应用越来越普遍，同时国内动平衡机研究成果层出不穷[1-7]，轮胎动平衡机研发和生产向高精度、高稳定性方向发展。

轮胎动平衡机都是以转子不平衡力激励下的响应作为测量对象。为确保平衡机具有较高的测量精度，机械结构的动力学模型建立的准确性便成为了平衡机设计中最为关键的环节之一。目前，针对动平衡机机械结构分析计算方面往往只考虑结构件的动力学特性，而忽略了轴承测量结果的影响，造成测量结果误差相对较大，测量数据随时间的推移以及机械结构工作状态的稍作改变而精度降低。本文基于轮胎动平衡机整机系统模型，分析了轴承对整机系统动态特性的影响，并进行实验验证，结果表明，考虑轴承的影响后，整机系统精度得到较大的提高。

1 模型的建立

采用Pro/E建立实体模型，在不影响计算结果的前提下，对机械结构进行有效简化。通过Pro/E与ANSYS之间的无缝接口，将模型导入到ANSYS中进行处理。所建实体模型如图1所示，其中标注的测量方向表示安装传感器的位置和测力方向。在分析中，将传感器简化为具有相应刚度的弹簧单元，单元类型选择为Combin14，三维实体模型单元类型选择为Solid45.

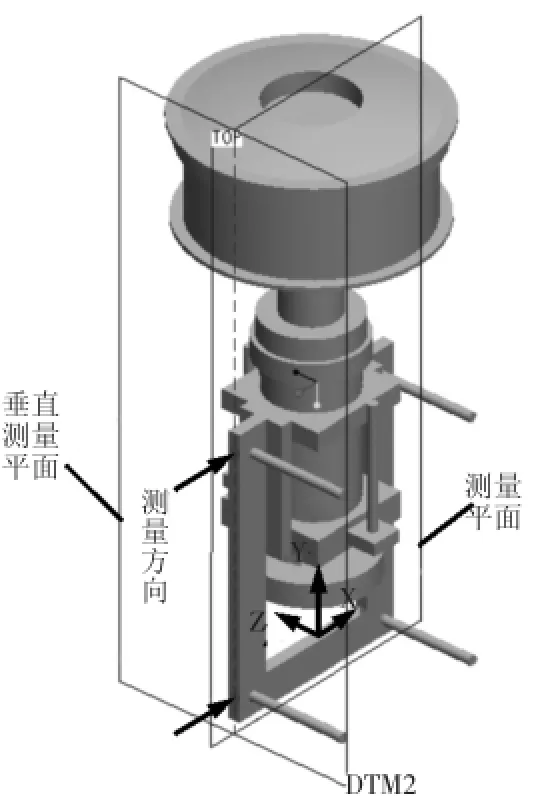
图1 动平衡机核心部件实体模型

2 系统的模态分析

2.1 不考虑轴承影响的模态分析

忽略轴承连接的影响，所有结构均按照实际材料属性进行设置，弹性杆、壳体及主轴均采用强度和刚度较大的材料，取其弹性模量为212 GPa，泊松比为0.28，密度为7 850 kg/m3；轮辋采用铝合金材料，取其弹性模量为71.7 GPa，泊松比为0.33，密度为2 810 kg/m3.前三阶振型如图2所示。

图2 不考虑轴承的模型前三阶振型

2.2 考虑轴承影响的模态分析

在主轴系统中，均采用角接触球轴承作为主轴支撑，主轴、轴承、壳体连接处示意如图3所示。

图3 主轴轴承安装示意图

在主轴系统的设计中，共采用两个7012C/DB型号的下轴承，背对背成对安装，三个7015C/DT型号的上轴承，串联安装。在角接触轴承的样本手册里查得，当主轴为轻型载荷时，7015型号的轴承预紧力为290 N，7012型号的轴承预紧力为250 N，其尺寸型号如表1所示。

表1 动平衡试验机所采用的轴承参数

采用角接触轴承经验公式[8]对轴承的法向和切向刚度进行计算，表达式如下：

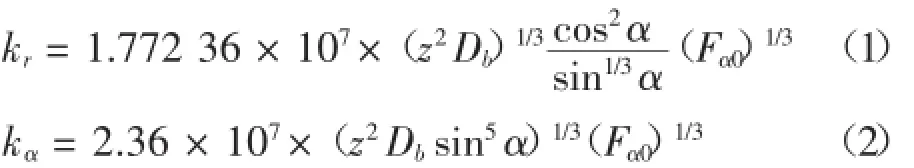
式中kr为径向刚度（N·m）；kα为轴向刚度（N·m）；z为轴承滚动体个数；Db为轴承滚动体直径（m）；α为轴承接触角（°）；Fα0为轴承预紧力（N）.

将上、下轴承的数据分别代入，可得，上轴承的刚度约为

下轴承的径向和轴向刚度约为

在模型分析中，主要关心传感器力测量平面和垂直力测量平面内的固有频率及振动特性，因此，在对轴承进行简化时，将轴承简化为上述两个垂直平面内的法向和切向弹簧，分布于主轴的周围，示意如图4所示。

图4 轴承简化模型示意简图

对含有轴承的模型进行模态分析，各阶振型如图5所示。

图5 考虑轴承影响的模型前三阶振型

由模态分析结果表明，当考虑轴承连接的影响时，整机的各阶固有频率均有显著下降，与不考虑轴承连接的分析结果相比，在测量平面内的固有频率下降了41.02%，如表2所示，可见轴承连接对整机的动态特性影响重大。

表2 不考虑和考虑轴承连接影响的两次分析结果对比

3 实验验证

借助虚拟仪器测试平台LabVIEW编写了测试程序，进行了激振实验。通过涡流传感器采集主轴旋转时的振动信号。选择主轴表面光洁度较好的部位作为涡流传感器的测量位置，采集主轴的振动信号。为避免动平衡机基架本身的振动影响，将涡流传感器固定在与动平衡机不接触的位置。激振方向与测量方向同相并处于同一个竖直平面，实际测量装置如图6所示。

图6 激振实验装置

实际测量时，外部激励信号为正弦扫频信号，选择步长为0.5 Hz，激振范围为0～300 Hz.在软件测试界面进行设置，由激振器将振动传递给动平衡机，通过涡流传感器采集振动信号，涡流传感器分辨率较高，对于低频信号也能精确识别。

通过上述激振实验，进行幅频特性分析发现，在97.3 Hz附近出现共振峰值，该值即为动平衡机一阶弯曲振型所对应的固有频率。将模型分析结果及激振实验结果相对比，误差为6.1%，分析结果与实验结果具有较好的一致性，说明模型建立正确，分析结果相对比较精确。如图7和表3所示。

图7 激振频域特性曲线

表3 实验结果与ANSYS分析结果对比

4 结束语

在轮胎动平衡系统建模过程中，考虑了轴承对系统动态特性的影响，采用有限元对整个系统进行仿真，并用实验进行验证，实验结果显示，系统建模过程中，考虑轴承的影响后，仿真结果与实验结果一致性较好，而不考虑轴承影响的动力学模型，一阶频率差别达30%以上，本文建模方法和实验结果对设计高精度轮胎动平衡系统有较大的指导意义。

[1]巫上清.动平衡机测量及远程监控系统研究[D].天津：天津大学，2009：15-20.

[2]李顺锋，程文平，张晓光，等.国产在线式轮胎动平衡试验机简介[J].轮胎工业，2005，25（09）：515-523.

[3]刘迎澍，尹建华，巫上清.基于复影响系数的载重轮胎动平衡机标定算法[J].天津大学学报（自然科学与工程技术版），2013，46（06）：565-570.

[4]牟世刚，冯显英，晏志文，等.基于小波分析的动平衡机不平衡量提取方法研究[J].山东大学学报（工学版），2011，41（03）：62-66.

[5]张宏辉，张万利.基于影响系数法的车轮平衡机检测系统[J].机械设计与制造，2007（07）：167-168.

[6]伍良生，洪豪，马建峰，等.轮胎动平衡机测试系统研究[J].机械设计与制造，2014（02）：34-36.

[7]刘健，潘双夏，杨克已，等.全自动动平衡机关键技术研究[J].浙江大学学报（工学版），2006，40（5）：777-782.

[8]肖毅川．考虑结合面特性的多段梁结构动态特性的研究[D]．北京：北京工业大学，2010：25-27．

Research on Influence of Bearings to Dynamic Characteristics of Tire Balancing Machine

MA Jian-feng1，ZHANG Yun-ze2，LI Chao1
（1.Mechanical Engineering and Applied Electronics Technology Institute，Beijing University of Technology，Beijing 100124，China；2.Harbin Institute of Technology，Affiliated High School，Harbin Heilongjiang 150086，China）

A three-dimensional solid model of tire dynamic balancing machine is modeled to research the modeling accuracy during the course of the tire dynamic balancing machine design.The model is imported into ANSYS for modal analysis.It is found that the bearing in the model has great influence on the analysis accuracy of the dynamic characteristics of the system，and the experimental results show that the finite element simulation and the experimental results are in good agreement.Therefore，in the tire dynamic balancing machine design,the influence of bearing must be considered.

balancing machine；bearings；modal analysis；excitation

TP391.7文献识别码：A

1672-545X（2017）02-0036-04

2016-11-23

马建峰（1979-），男，山西朔州人，博士，讲师，主要研究方向为精密、超精密制造装备。