聚酯玻璃钢大气老化力学性能BP人工神经网络预报模型的建立

杜武青，刘颖慧，赵晴，王莹，马达兵



聚酯玻璃钢大气老化力学性能BP人工神经网络预报模型的建立

杜武青1，刘颖慧1，赵晴2，王莹1，马达兵3

（1.北京理工大学珠海学院 材料与环境学院，广东 珠海 519085；2.南昌航空大学 材料科学与工程学院，南昌 330063；3.中国人民解放军91515部队，海南 三亚 572016）

目的准确地分析并建立起一个老化模型，探究不饱和聚酯玻璃钢在大气环境中的条件与老化性能的变化联系。方法在气象数据的基础上分别分析不饱和聚酯玻璃钢在不同季节不同大气环境下各种力学性能的变化，利用数学建模的人工智能方法-BP神经网络进行建模。结果实际值与预测值有很好的一致性，模型精确度也较高。结论此预报模型可比较精确地评价不饱和聚酯玻璃钢在大气中的老化行为。

不饱和聚酯玻璃钢；大气老化；人工神经网络

不饱和聚酯玻璃钢具有质量轻、强度高、耐腐蚀性能好、电性能好、成本低和工艺性能良好等优点，是可普遍适用于人们生活中的一类高分子材料，但弹性模量低、长期耐温性差及层间剪切强度低等不足也是使用玻璃钢时不可忽视的因素[1]。随着玻璃钢在大气环境中的广泛使用，其中老化现象尤为突出。最为明显的现象包括：玻璃钢表面的颜色发生变化，表面的树脂发生脱落，各种力学性能逐渐下降，最终出现老化现象，即丧失了其使用的价值[2]。因此，为了使得不饱和聚酯玻璃钢在大气环境下更安全更长久的使用，研究玻璃钢的老化问题渐渐成为了人们关注的焦点。

由于玻璃钢老化过程复杂和不易监测，对于老化的研究主要集中在对影响老化的环境因素进行研究，有对温度、湿度、辐照量、温差、臭氧、紫外线等进行单因子或多因子复合作用机理的研究[3—7]。对老化方式和方法的研究，有自然环境老化、氙灯人工加速老化、荧光紫外光人工加速老化、人工酸雨环境老化等自然或人工老化的研究[8,10]。对老化过程中和老化后材料性能的表征研究，有运用力学性能、X射线光电子能谱、热分析法、色谱/质谱分析法、正电子湮灭寿命谱法、核磁共振波谱法、拉曼光谱法进行表 征[11,13]。对老化后性能预测模型的研究，有相关分析法、模糊数学法、灰色关联分析法、Hop field网络模型等模型进行预测[14—15]。文中通过神经网络数学建模的方法对不饱和聚酯玻璃钢在大气中的老化进行了探究，利用网络模型来评价不饱和聚酯玻璃钢在大气环境下力学性能的老化，从而能够大量减少人力物力的损耗，也能减少试验的周期性，能在高效短时的情况下得出可靠的试验结论[16]。

1 预测神经网络模型的建立

1.1 BP神经网络模型的建立

由于BP神经网络与其余的理论建模相比，建模关系数量不受限定，灵便性和预报准确度比较高，将其应用于不饱和聚酯玻璃钢的老化预测，是一种更为实用的模型。BP神经网络用来预测材料的性能变化具有操作方法简单、误差小、容错性强、学习精度高等优点，如图1所示。

BP神经网络分为三个部分，分别为输入层、隐含层、输出层。从数学的角度上对BP神经网络模型进行分析，由第一部分可以得到关于BP神经网络模型的第一个公式[17]：

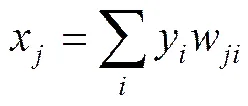
对于神经元的输出函数，模型单元节点通常选用Sigmoid函数[18]：

(2)

通过式(1)和式(2)，可以分析出BP神经网络输出结果的计算过程。每个神经元受到刺激y，然后加权积累权重w，完成产生x，再通过Sigmoid函数产生y，向下一层与它相连的神经元传递，依次类推最终输出结果。

权重为w，需要用数学推导来修正w得到误差量。用d表示正确结果，那么误差可推导出公式：

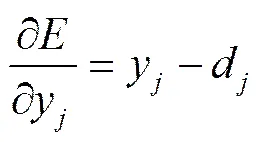
因此权重w的误差量就是，由式(1)可推 导出：

(4)

结合式(2)和(4)可推导出：

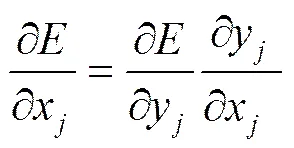
最终得到的误差量的值为：

(6)

最后修正权重w，再设置一个0到1之间的学习率：

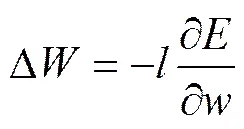
在整个训练的过程中，反复的计算输入和输出误差，直到网络的平均误差达到要求为止[19]。

1.2 老化力学性能网络的建立

文中主要研究大气中的温度、辐照量、湿度及温差对玻璃钢的影响，其性能随影响因素的变化过程。根据BP神经网络特点和输入输出情况，将设定4个输入参数和5个输出参数，即网络的输入层有4个单元，输出层为有5个单元。输入参数为温度、辐照量、湿度及温差影响因素；输出参数为纯树脂样条的弯曲强度、玻璃钢剪切强度、玻璃钢表面涂层的弯曲强度、玻璃钢拉伸强度、玻璃钢剪切强度。

BP神经网络隐含层的层数和节点数是与输入层和输出层单元相关。一般来讲，隐含层、隐藏节点越多，则精度越高，但网络的泛化能力也随之下降。神经网络结构的优化，尚缺乏通用的理论指导，一般是根据应用的不同而不同。实际运用中，一般采用的方法就是不断地尝试，即比较多种网络结构，参考一些建议，最后确定一种比较好的结构。Cybenko证明，三层网络（一层隐含层）如果有足够多的隐藏节点，可以逼近任何函数，因此较少的隐藏层是可以胜任的[20]。在常用的网络结构中一般采用1~3个隐含层。

隐含层节点的作用是从样本中提取并存储其内在的规律，每一个隐节点有若干个权值，而每个权值都是增加网络映射能力的一个参数。隐藏层节点数太少时，网络每次学习时间相对较短，网络从样本中获取信息的能力较差，不足以概括和体现样本规律，从而识别新样本困难，容错性差；隐含层节点数太多时，网络的学习时间加长，且学习过程中，有可能把样本中非规律性的内容（如噪声等）也学习记住，从而出现所谓的“过度吻合”问题，反而降低了泛化能力。设置多少个隐含层节点，取决于训练样本数的多少以及样本中蕴含规律的复杂程度等多种因素。目前常用于确定节点的方法有：取输入单元和输出单元数之和的均值；最佳隐含层节点数为输入层单元与输出单元数之积开平方；取小于输入层的个数即可；取（输入层单元+1）/2或（输入层－1）；取输入层单元数的对数；取（输入层节点数+1）的2倍。BP网络设计中初始权值是网络映射能力的一个参数，权值的恰当与否，主要体现在整个网络的收敛和学习时间的长短。恰当的权值，可以缩短网络学习的时间，反之则增加网络学习的时间，但不影响学习的结果。

文中模型设定两个隐含层，如图2所示。其中各层的神经元个数取输入层和输出层单元之和的均值，分别为4和5。两个隐含层及输出层所计算的转移函数为{‘tansig’，‘tansig’，‘purelin’}，训练函数为‘trainrp’。对于初始权值，由于大气中的温度、辐照量、湿度及温差对玻璃钢影响的权重因各地的气候条件不同而未确定，故采用等同权重进行学习。

图2 BP网络结构模型

2 老化性能计算

2.1 训练误差

构建一个BP网络模型，首先要学习的是样本中的训练网络，利用Mapminmax函数预先把数据进行归一化处理，即规格化。将全部数据规格到[0，1]这个区间，进行网络空间的变化，以此来保证网络模型能够正常运行。该次模型网络的训练次数设定阈值为1000次。如图3所示，如果模型其中一个训练，训练了10次后，训练误差平缓趋向于0，仅训练10次，便得到了一个较为精确的预测，学习精度可达到0.000 000 001，获得的训练误差平均值为0.34%。

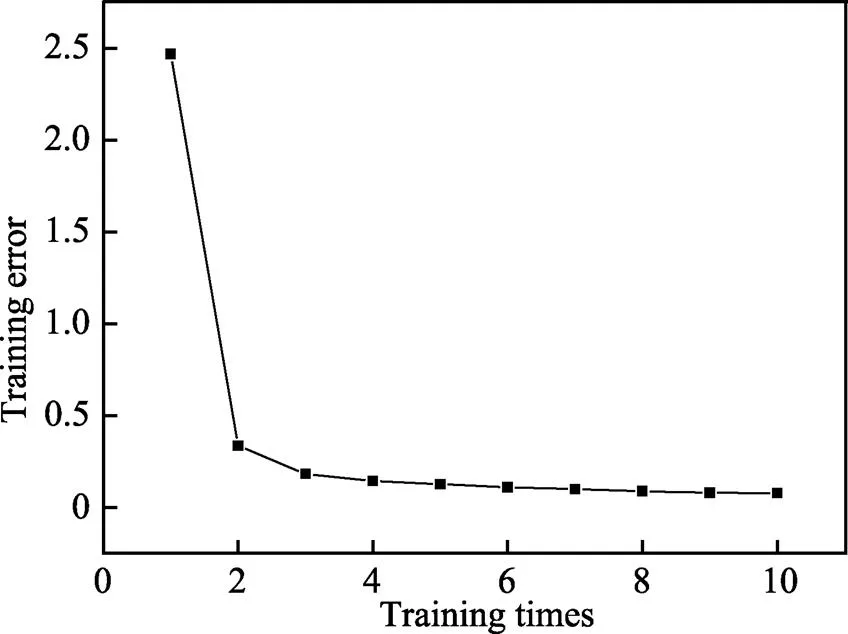
图3 BP神经网络训练误差曲线

BP神经网络模型的算法是利用梯度下降的原理来实现的，为了避免造成局部极小值等问题，最好的方法是加大训练量。第一次的训练误差接近2.5%，而当第二次训练开始时，训练误差极速减小，10次之后趋向为0。由此可知，训练越多次，学习的精度越高。由建立BP神经网络模型训练过程可得出，网络的误差相对较小，这足以说明，构建BP神经网络模型是可以比较精确地预测及评价玻璃钢在大气环境中的老化。

2.2 预测数据

以所采取的数据为例，输出层是根据实验所测得的五个玻璃钢力学性能所组成，分别为纯树脂样条的弯曲强度、玻璃钢弯曲强度、玻璃钢表面涂层弯曲强度、玻璃钢拉伸强度、玻璃钢剪切强度。构建BP神经网络模型后，通过对这五种性能实际值预测值的一一分析，进行预测对比，来证明构建BP神经网络模型对不饱和聚酯玻璃钢老化力学性能进行评价是否可行。结果如图4—8所示。

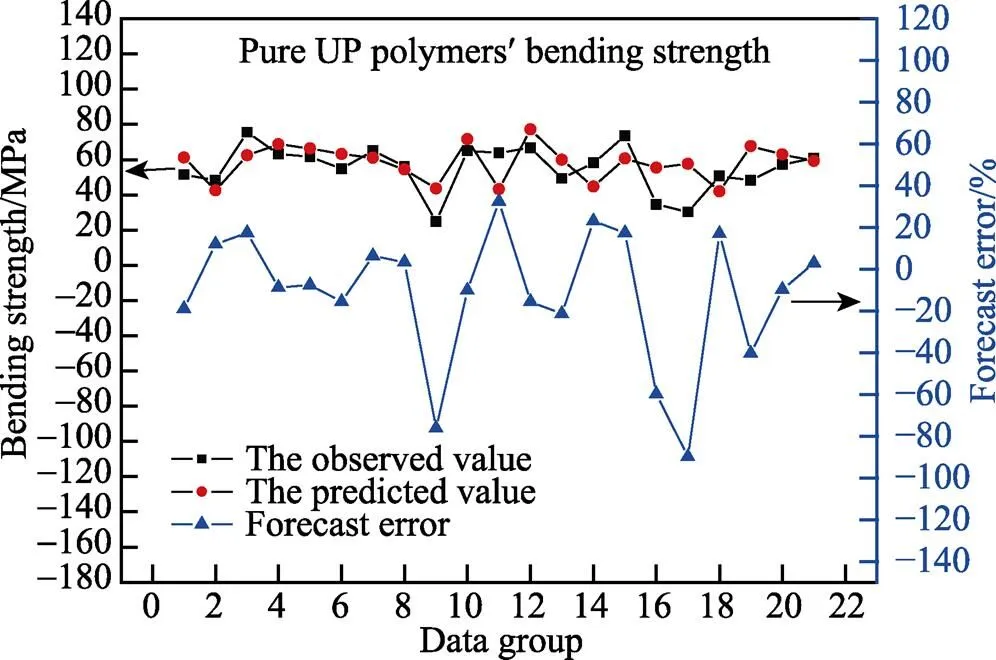
图4 BP网络预测纯树脂弯曲强度的结果

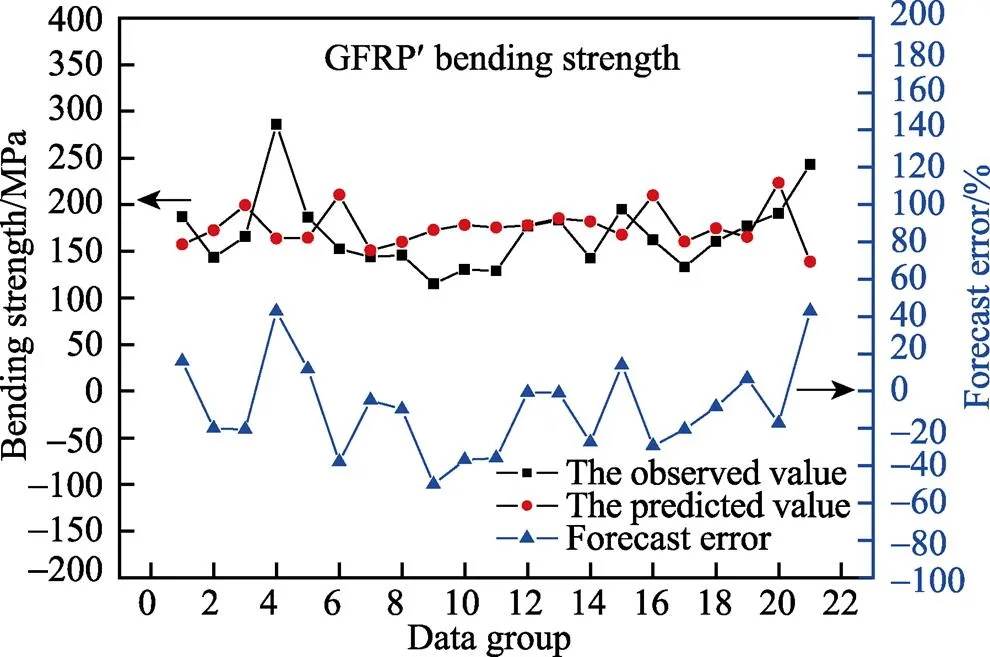
图5 BP网络预测玻璃钢弯曲强度的结果

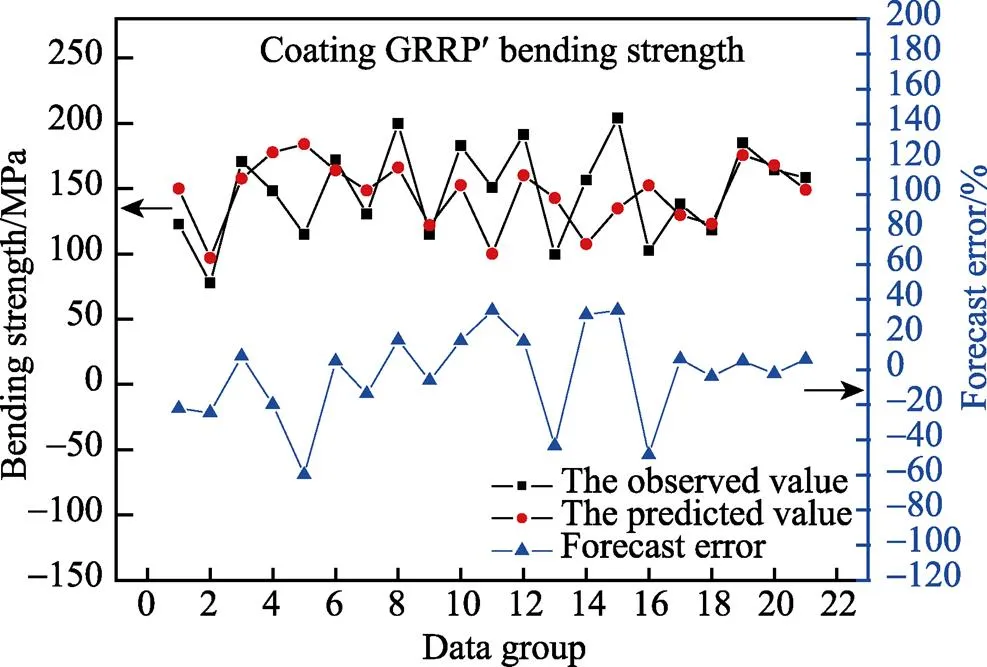
图6 BP网络预测玻璃钢表面涂层弯曲强度的结果

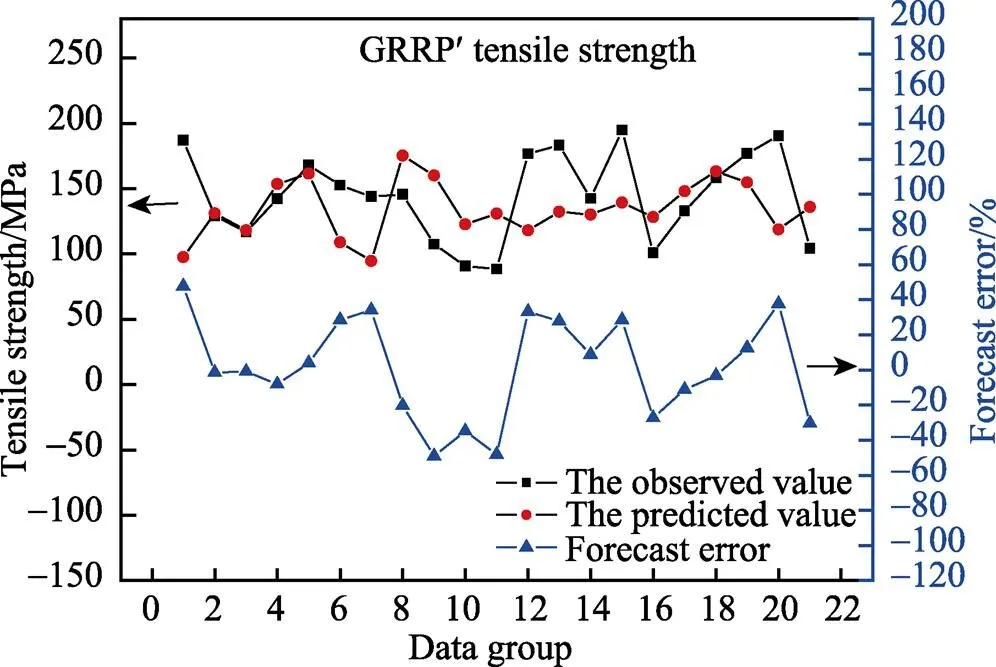
图7 BP网络预测玻璃钢拉伸强度的结果

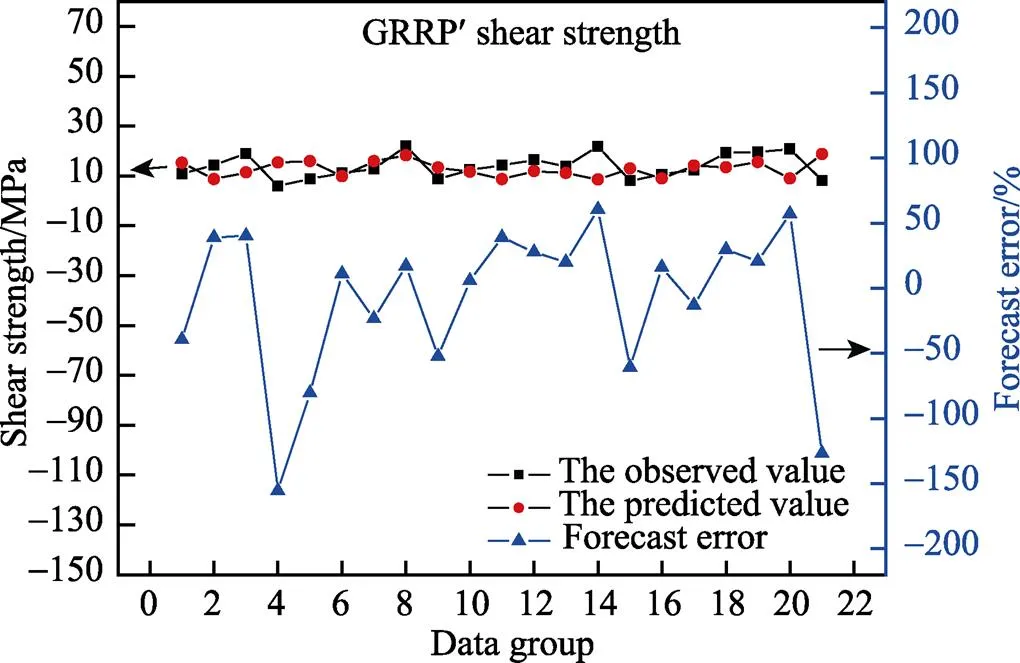
图8 BP网络预测玻璃钢剪切强度的结果

2.3 分析讨论

由图4可知，纯树脂的弯曲强度实际值比预测值起伏更大，但都还是在围绕0点水平线上下浮动。其中最大误差为89.89%，最小误差为2.81%，平均误差值为11.55%。由图5可知，不饱和聚酯玻璃钢弯曲强度与预测值略有偏差．其中最大误差为49.99%，最小误差为0.62%，平均误差值为8.88%。由图6可知，带有涂层的不饱和聚酯玻璃钢的弯曲强度实际值与预测值偏差具有先较大后变小的趋势。其中最大误差为59.86%，最小误差为2.18%，平均误差值为3.14%。由图7可知，不饱和聚酯玻璃钢的拉伸强度实际值与预测值具有相同的变化趋势。其中最大误差为49.02%，最小误差为0.94%，平均误差值为1.31%。由图8可知，不饱和聚酯玻璃钢剪切强度实际值与预测值曲线非常接近，但其误差却较大。其中最大误差为155.64%，最小误差为5.58%，平均误差值为8.05%。

由此可见，平均误差值都小于15%。其中最小的是不饱和聚酯玻璃钢的拉伸强度，最大的是纯树脂的弯曲强度。玻璃钢拉伸强度与增强材料玻璃纤维的强度关系较大，外界环境对玻璃钢中玻璃纤维的腐蚀不易，而纯树脂的弯曲强度则与树脂的状态密切相关，外界环境对纯树脂的老化比腐蚀玻璃纤维容易，并且纯树脂在制样等环节会受到很多因素干扰。因此，玻璃钢拉伸强度测量值的稳定性好于纯树脂弯曲强度的测量值，则BP神经网络系统对于玻璃钢拉伸强度的预测值要好于纯树脂强度。

不饱和聚酯玻璃钢弯曲强度与剪切强度平均误差值相当，但剪切强度比弯曲强度的误差波动值大。玻璃钢弯曲强度是玻璃纤维与树脂的共同抗弯作用产生的，剪切强度则是玻璃纤维与树脂之间的层间结合力产生的。对比发现，弯曲强度的值远大于剪切强度值，数值越小受到加工测量的影响越明显，则BP神经网络系统对于弯曲强度的预测值要好于剪切强度。

带有涂层的不饱和聚酯玻璃钢弯曲强度比不带涂层的不饱和聚酯玻璃钢的平均误差值要小，但波动值要大。可能原因是带涂层的聚酯玻璃钢延缓了外界环境对树脂的老化降解，但涂层的不均匀性也导致了降解的不均匀性，进而影响其弯曲强度值的波动。则BP神经网络系统对于带有涂层的不饱和聚酯玻璃钢的预测误差小，但波动大。

文中建立的BP神经网络系统对五个玻璃钢力学性能的预测效果较好，预测效果的优良顺序是：不饱和聚酯玻璃钢拉伸强度>带有涂层的不饱和聚酯玻璃钢弯曲强度>不饱和聚酯玻璃钢弯曲强度>不饱和聚酯玻璃钢剪切强度>不饱和聚酯纯树脂的弯曲强度。

3 结论

文中对不饱和聚酯玻璃钢在大气环境下老化的力学性能进行BP神经网络建模，通过对结果的逐一分析，基本确认正确的网络输入-输出关系已经建立。

1）根据大气环境因子、力学性能测试种类和常用BP网络神经模型，确定了BP神经网络模型有4个输入层、2个隐含层、5个输出层。

2）在BP神经网络的学习中，训练次数与精准度呈正相关性，训练次数越多，精准度越高，误差越接近于0。当误差逐渐接近于0，且变化平稳时，系统便认定训练次数，绘制出训练误差曲线图，完成BP神经网络模型的建立。

3）通过建立的BP神经网络模型对纯树脂样条弯曲强度、玻璃钢剪切强度、玻璃钢表面涂层的弯曲强度、玻璃钢拉伸强度、玻璃钢剪切强度等五个力学性能参数进行预测，得到实际值与与预测值平均误差分别为11.55%，8.88%，3.14%，1.31%，8.05%。对不饱和聚酯玻璃钢在大气下老化后力学性能的变化有很好的预测性。

4）通过建立的BP神经网络模型的预测优良顺序为：不饱和聚酯玻璃钢拉伸强度>带有涂层的不饱和聚酯玻璃钢弯曲强度>不饱和聚酯玻璃钢弯曲强度>不饱和聚酯玻璃钢剪切强度>不饱和聚酯纯树脂的弯曲强度。

[1] 朱春芽. 不饱和聚酯玻璃钢的加速老化研究[D]. 南昌: 南昌航空大学, 2008.

[2] 王禹阶, 崔鹏. 玻璃钢与复合材料的生产及应用[M]. 合肥: 合肥工业大学出版社, 2005.

[3] 解昊. 聚丙烯无纺布的光老化与降解[D]. 广州: 华南理工大学, 2012.

[4] 闫永生. 不同光源条件下PVC涂层膜材料光氧老化性能研究[D]. 上海: 东华大学, 2012.

[5] 赵锦灿, 杨俊龙. 光缆护套的热氧与光氧加速老化研究[J]. 塑料工业, 2015, 43(12): 87—92.

[6] 滕旭秋, 费占黎. 多因素作用下橡胶沥青老化特性研究[J]. 兰州交通大学学报, 2016, 35(4): 1—5.

[7] 代军, 晏华. 不同类型聚乙烯光氧老化特性比较研究[J]. 工程塑料应用, 2016, 44(8): 88—92.

[8] LEE B L, HOLL M W. Effect of Moisture and Thermal Cycling on Inplane Shear Properties of Graphite Fibre- reinforced Cyanate Ester Resin Composites[J]. Composites Part A:Applied Science and Manufacturing, 1990, 27(11): 1015—1022

[9] 王仲昭. 材料耐光老化测试研究[J]. 纺织检测与标准, 2016(4): 7—11.

[10] 周威, 文俊. 环氧沥青在模拟自然条件下的老化机理研究[J]. 胶体与聚合物, 2016, 34(3): 122—124.

[11] OTIENO-ALEGO V, CREAGH D, JAR B, et al. Characterization of the Moisture Absorption and Thermal Ageing Behavior of Polymeric Composite Systems Using Raman Spectroscopy[C]// First International Conference on Ageing Studies and Lifetime Extension of Materials, UK: Oxford, 1999: 113—121.

[12] 杜武青, 赵晴. XPS研究不饱和聚酯人工加速老化行为[J]. 工程塑料应用, 2010, 38(6): 60—63.

[13] 刘玉兰, 韩明哲. 红外光谱法在SBS老化评价中的应用[J]. 分析仪器, 2016(5): 53—55.

[14] 谢红梅, 黄伟. 塑料自然老化力学性能的人工神经网络预测[J]. 工程塑料应用, 2001, 29(12): 31—33.

[15] 黄伟, 仇君. 塑料自然老化力学性能的灰色预测[J]. 广西大学学报(自然科学版), 2001, 26(4): 275—277.

[16] 王玉民, 宁培森. 不饱和聚酯树脂玻璃钢(GFRP)的老化研究进展[C]// 塑料制品老化与防老化技术研讨会. 广州, 2011.

[17] 方明. 基于BP神经网络的电网工程估价模型研究[J]. 科技咨询, 2008(35): 20.

[18] 胡雪棉. 基于BP神经网络的中国煤炭资源需求预测模型研究[D]. 太原: 山西财经大学, 2008.

[19] 赵朝凤, 令晓明. 浅析BP神经网络基本模型的C语言实现[J]. 通讯技术, 2013, 46(1): 89—91.

[20] 殷震. 基于BP神经网络的电力变压器内部故障诊断方法研究[D]. 天津: 天津大学, 2007.

Establishment of Prediction Model for GFRP¢s Mechanical Property in Atmosphere Aging Based on BP Neural Network

DU Wu-qing1, LIU Ying-hui1, ZHAO Qing2, WANG Ying1, MA Da-bing3

(1.Department of Materials and Environment, ZHBIT, Zhuhai 519085, China; 2.Department of Material Science and Engineering, Nanchang HangKong University, Nanchang 330063, China; 3.Troops 91515 of PLA, Sanya 572016, China)

Objective To analyze accurately and establish an aging model to explore conditions of fiberglass reinforced plastic in atmospheric environment and relations in change of its aging properties. Methods Changes of fiberglass reinforced plastic’s mechanical properties in different atmospheric environments of different seasons were analyzed based on the meteorological data and a model was established with artificial intelligence method-BP neural network of mathematical modeling. Results The actual value and predicted values were in good agreement and the model accuracy was high. Conclusion The prediction model can evaluate aging behaviors of unsaturated fiberglass reinforced plastic in the atmosphere accurately.

unsaturated fiberglass reinforced plastic; atmospheric aging; artificial neural network

10.7643/ issn.1672-9242.2017.05.021

TJ04; TQ317.6

A

1672-9242(2017)05-0097-05

2016-12-01；

2017-01-30

国家自然科学基金重点项目（50533060）

杜武青（1984—），男，江西人，硕士，主要研究方向为高分子材料的老化、加工和改性。