多并网逆变器耦合谐振特性*

朱小会， 袁玉霞， 张庆辉

(1. 郑州科技学院 电气工程学院， 郑州 450064； 2. 河南工业大学 信息科学与工程学院， 郑州 450001)

多并网逆变器耦合谐振特性*

朱小会1， 袁玉霞1， 张庆辉2

(1. 郑州科技学院 电气工程学院， 郑州 450064； 2. 河南工业大学 信息科学与工程学院， 郑州 450001)

针对多LCL滤波型并网逆变器并联并网系统的复杂耦合谐振问题，建立单台逆变器的数学模型，并扩展成多台逆变器并联系统的数学模型.考虑逆变器自身、并联逆变器和电网单独作用时的等效电路模型，提出一种基于叠加定理的多逆变器并联系统小信号等效简化电路.利用频域分析法仿真分析了多逆变器并联的耦合谐振特性，并与单台逆变器谐振特性进行了对比分析，结果表明，多逆变器并联系统会出现额外的谐振尖峰，且谐振峰值和频率与并联逆变器的数量有关.

LCL滤波； 并联； 耦合； 谐振； 数学模型； 叠加定理； 频域分析

随着常规化石能源的不断枯竭和生态环境的日益恶化，光伏并网发电等可再生能源因其产量丰富、高效、无污染等特点受到广泛的关注与重视[1-2].并网逆变器作为光伏阵列和电网的接口，其性能对并网系统的安全稳定起着至关重要的作用，然而，随着大量电子器件的接入，并网逆变器产生大量的高频谐波而影响系统的高效稳定运行[3].

传统的抑制高频谐波方法是在逆变器和电网接口处串入单电感L滤波器，为了提高抑制高频谐波的能力，往往需要将电感值设计的很大，这样又会带来功率密度低、占用体积大和高功耗等缺点.而LCL滤波器因高频滤波效果好、体积小等优势而得到广泛的应用[4-6].在同样的功率等级系统和取得相同的滤波效果条件下，LCL滤波器所需的电感值要小得多，这大大提高了系统的功率密度并且节省了体积.尽管LCL滤波器具有多种优势，但是它是一个三阶网络，在谐振频率处有一个较大的谐振峰值，会导致谐波放大，引起谐振问题.

为有效抑制LCL滤波器固有的谐振问题，国内外学者也进行了大量的研究，然而目前大部分的研究工作仅仅针对单台LCL逆变器[7-9].在实际应用中，尤其是在高渗透率的分布式光伏发电系统和大型光伏电站中，LCL并网逆变器往往都是以并联的形式接入电网，系统中的谐振问题较单电感而言要复杂的多，不仅与自身滤波参数有关，而且各逆变器的LCL滤波器是相互耦合在一起的，形成复杂的高阶网络.

为深入分析该复杂谐振问题，本文以多光伏并网逆变器并联系统为例，建立了其等效数学模型并求出传递函数，基于此利用Bode图仿真分析了耦合谐振频谱特性，并与单LCL逆变器谐振特性进行了对比.

1 多LCL滤波器的逆变器并联系统

含多个LCL滤波器的逆变器并联系统如图1所示，图中，u11、u21、un1分别为1、2和n号逆变桥侧输出电压；L11、L21、Ln1分别为1、2和n号逆变桥侧滤波电感；C1、C2、Cn分别为1、2和n号逆变器滤波电容；L12、L22、Ln2分别为1、2和n号逆变器网侧滤波电感；i12、i22、in2分别为1、2和n号逆变器输出电流；ig为所有逆变器输出电流之和，即入网电流.

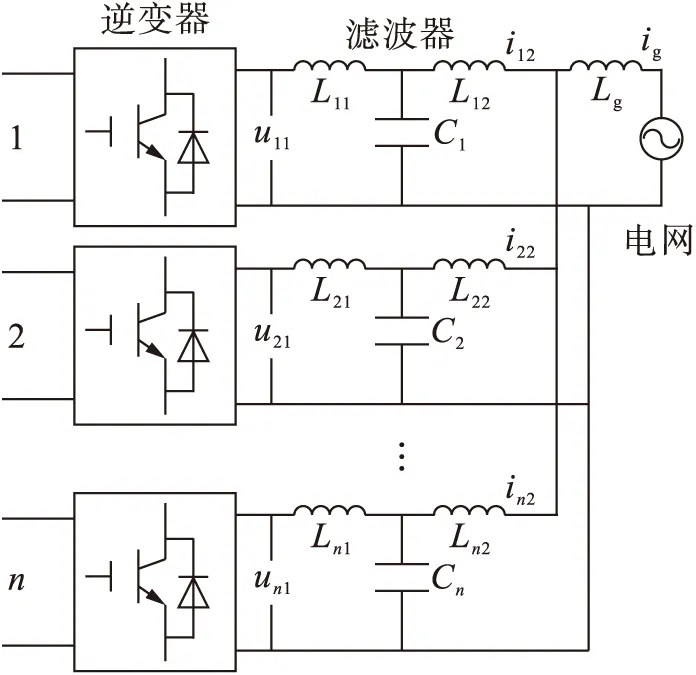
图1 多LCL滤波型并网逆变器并联并网系统

一般情况下，同一光伏电站采用同类型的并网逆变器，因此本文中假设每台并网逆变器的LCL滤波器都是一样的，即

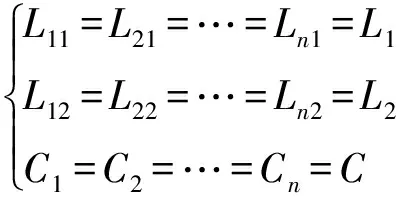
(1)

2 逆变器并联并网系统建立

假设所有并网逆变器都具有相同的参数，结合并网逆变器的电源特性可将图1等效为多种电源激励作用下的结构框图，如图2所示.由图2可知，多并网逆变器并联系统可等效为多个电源共同作用下的并联电路.根据电路叠加定理[10]，多种电源作用效果可以等价为每一个电源单独作用，然后将每个作用结果进行叠加的效果.本文基于该原理，以第1号逆变器输出电流为分析对象，其输出特性是由1号逆变器自身、与其并联的2～n号逆变器以及电网等三种激励源共同作用而决定的.在该三种激励源单独作用下，对多LCL型并网逆变器并联系统的耦合复杂谐振特性进行了深入地数学推导和分析.

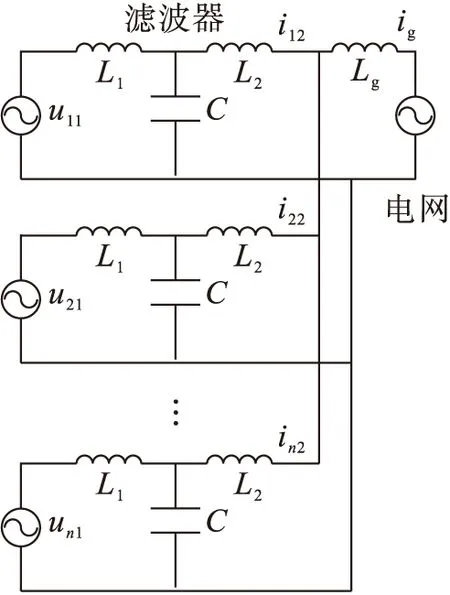
图2 多LCL滤波型逆变器并联等效电路

2.1 逆变器自身作用

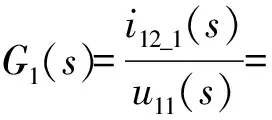
(2)

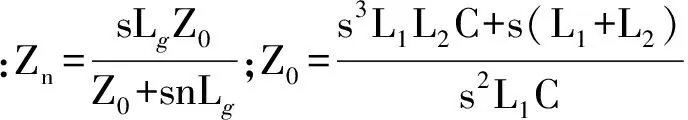
从式(2)可以看出，1号逆变器输出电流到1号逆变桥输出电压的传递函数是一个较为复杂的高阶网络，其传递特性不仅与滤波器参数、电网等效电感参数有关，还和并联系统的并网台数紧密相关.

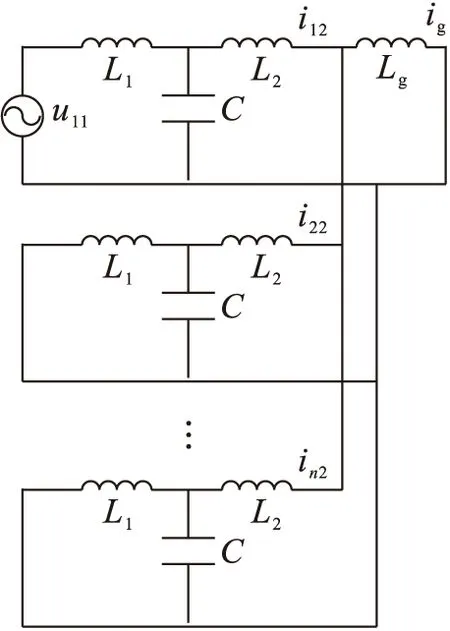
图3 1号逆变器作用等效电路

2.2 逆变器并联作用

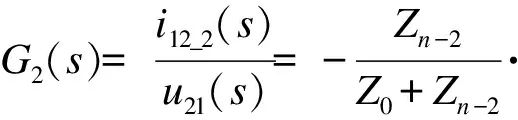
(3)

从式(3)可以看出，1号逆变器输出电流到2号逆变桥输出电压的传递函数是一个高阶网络，比式(2)表现出了更高的阶数和更为复杂的传递特性.其传递特性也与滤波器参数、电网等效电感参数和并网台数有关.

2.3 电网电压串联作用

在图2中当只有电网电压单独作用时，其他电压源可看成短路状态，其等效电路如图5所示.根据图5可以求得1号逆变器输出电流到电网电压的传递函数为

(4)

从式(4)可以看出，1号逆变器输出电流到电网电压的传递函数较式(2)和式(3)而言阶数低一些，复杂程度略低.其传递特性与滤波器参数和电网等效电感参数有关.

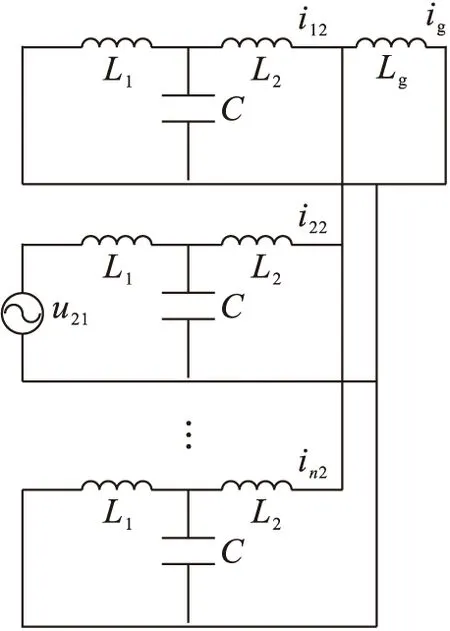
图4 2号逆变器作用等效电路

图5 电网电压作用等效电路

上述研究分析了各个激励源对1号逆变器输出电流的传递特性，根据线性叠加原理，可将三部分作用相加，求出在多LCL型并网逆变器并联系统中1号逆变器输出电流的表达式为

i12(s)=i12_1(s)+i12_2(s)+i12_3(s)

(5)

3 耦合谐振特性分析

将单台LCL滤波型并网逆变器和多LCL滤波型并网逆变器并联系统传递函数(2)、(3)、(4)分别在Matlab中画出对应的伯德图，仿真中分别采用1、3、6、9和12台逆变器进行分析.

图6是当只有1台LCL型并网逆变器并网系统输出电流到逆变桥侧输出电压的传递函数伯德图.从图6中可以看出，系统较高频段只有一个谐振峰，且频率固定.

图7是仅当1号逆变器作用下的伯德图，其对应的传递函数为式(2).与图6相比，该系统具有两个正的谐振尖峰值和一个负的谐振尖峰.其中谐振频率高的谐振峰不会因并网逆变器并联的数目变化而变化，为一固定的谐振峰和谐振频率.

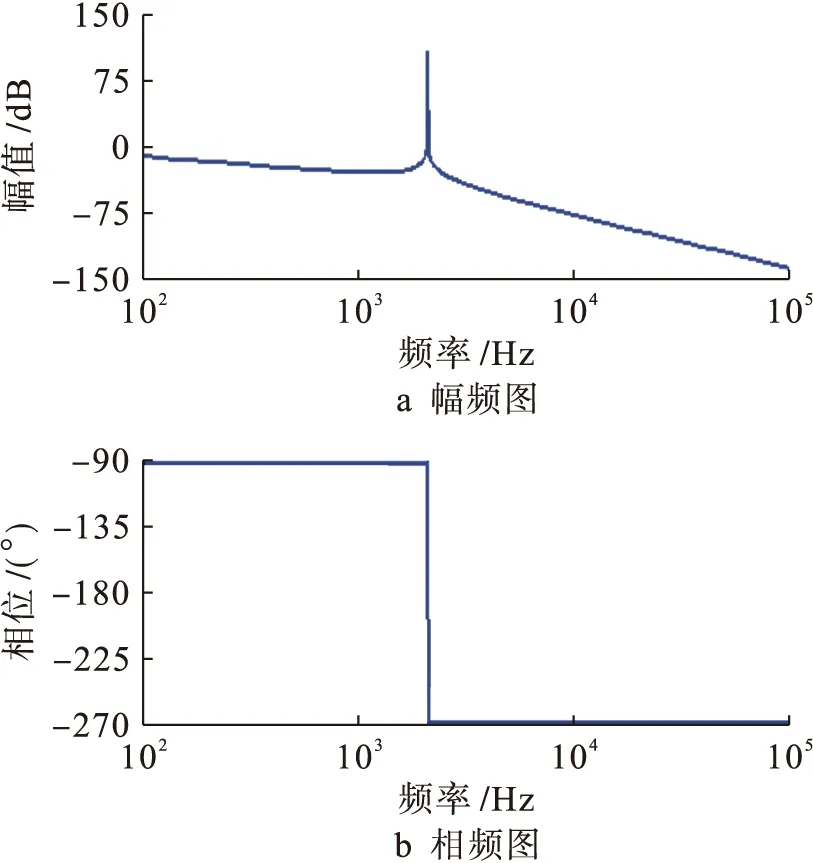
图6 单台LCL滤波器的伯德图

而谐振频率较小的正谐振峰和负谐振峰都会随着并网逆变器并联数目的增多不断地向频率减小的方向移动，即并联数量越多，谐振频率越小.

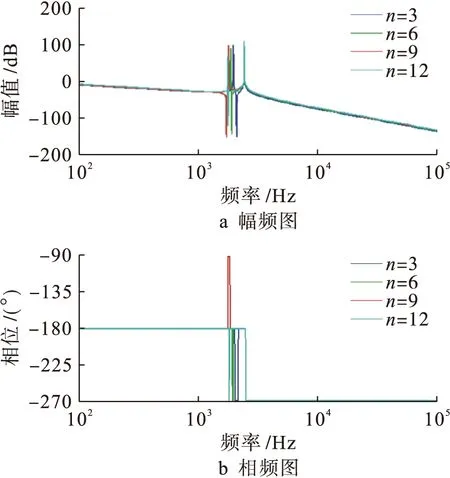
图7 1号逆变器作用下的伯德图

图8是当2号逆变器作用下的伯德图，其对应的传递函数为式(3).与图6相比，该系统也具有两个正的谐振尖峰值和一个负的谐振尖峰值.其中谐振频率高的正谐振峰和负谐振峰都不会因并网逆变器并联的数目变化而变化，而谐振频率较小的正谐振峰会随着并网逆变器并联数目的增多不断向频率减小的方向移动，即并联数量越多，谐振频率越小.

图9为电网电压作用下的伯德图，其对应的传递函数为式(4).与图6相比，该系统只存在一个正的谐振尖峰和一个负的谐振尖峰.其中，正谐振峰会随着并网逆变器并联数目的增多不断地向频率减小的方向移动，即并联数量越多，谐振频率越小.负谐振峰不会因并网逆变器并联的数目变化而变化，为固定的谐振峰和谐振频率.

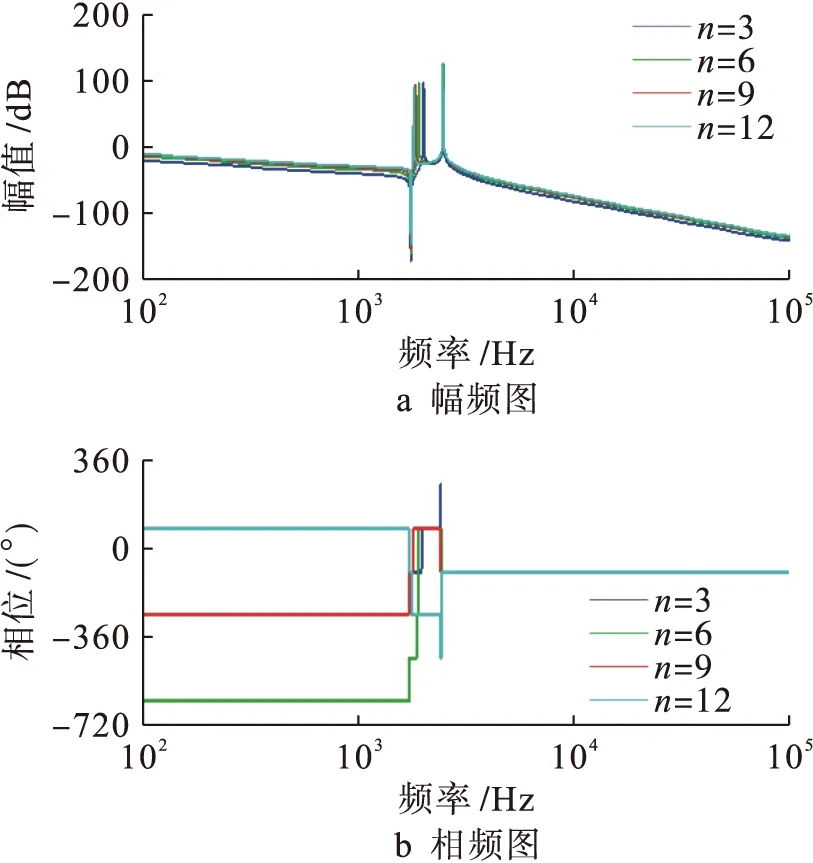
图8 2号逆变器作用下的伯德图

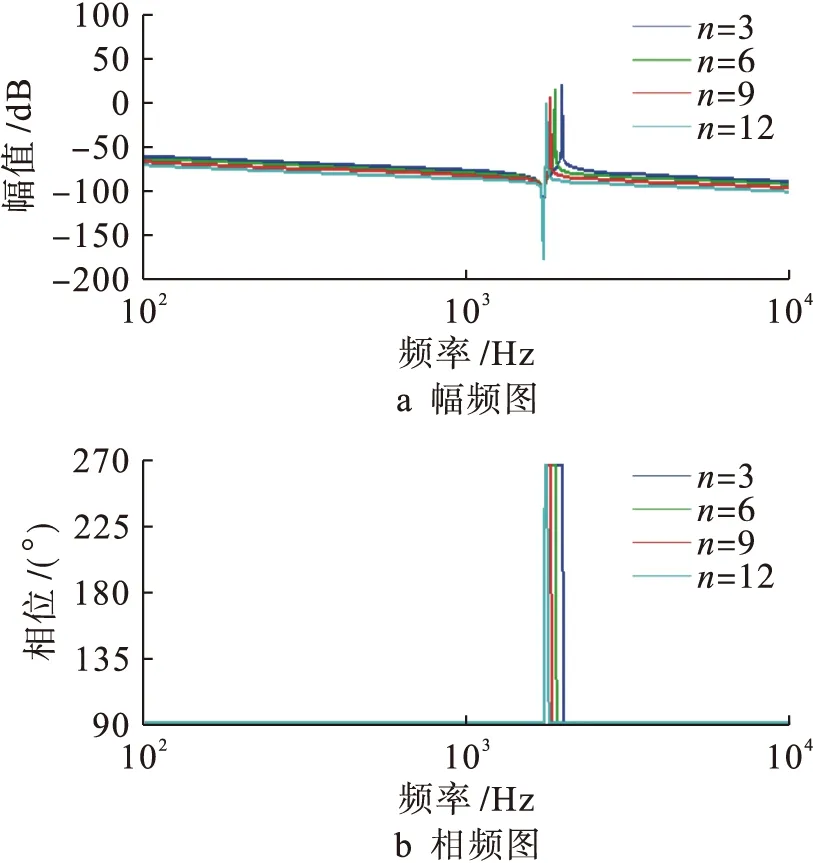
图9 电网电压作用下的伯德图

由图7～9可知，较单台LCL滤波器的传输特性而言，多LCL滤波型逆变器并联并网系统具有更为复杂的耦合谐振特性，系统具有额外的谐振尖峰，且谐振峰值与谐振频率均与并网台数有关.

4 结 论

本文建立了多LCL型逆变器并联并网系统的数学模型，以分析1号逆变器输出电流为例，获得了在1号逆变桥输出电压、2号逆变桥输出电压和电网电压3种不同激励源作用下的传递函数特性.基于此在伯德图上仿真分析了耦合谐振特性，并与单LCL型逆变器谐振特性进行了对比，分析结果表明：

1) 采用的叠加频域分析方法能够清楚地分析多并网逆变器耦合谐振特性，对后续设计谐振抑制措施具有指导意义；

2) 多逆变器系统较单LCL滤波系统而言，具有额外的谐振尖峰，且谐振峰和谐振频率均与并网台数有关.

[1]常瑜.中国光伏发展报告：2011 [M].北京：中国环境科学出版社，2011.

(CHANG Yu.China development report of PV：2011 [M].Beijing：China Environmental Science Press，2011.)

[2]熊燕，刘鑫，马胜红.中国城市规模化光伏发电应用条件分析 [J].可再生能源，2012，30(1)：123-126.

(XIONG Yan，LIU Xin，MA Sheng-hong.Application condition analysis for scaled PV power generation in urban area of China [J].Renewable Energy Resources，2012，30(1)：123-126.)

[3]王湘明，张玮玮，王卫鑫.并网逆变器功率和合成谐波阻抗联合控制策略 [J].沈阳工业大学学报，2016，38(2)：127-132.

(WANG Xiang-ming，ZHANG Wei-wei，WANG Wei-xin.Combined control strategy of power and synthetic harmonic impedance for grid connected inverter [J].Journal of Shenyang University of Technology，2016，38(2)：127-132.)

[4]金亮亮，周荔丹，姚钢，等.适用于并网逆变器的新型LCL滤波器 [J].电力系统保护与控制，2016，44(11)：1-8.

(JIN Liang-liang，ZHOU Li-dan，YAO Gang，et al.A novel LCL filter adopted in grid-connected inverter [J].Power System Protection and Control，2016，44(11)：1-8.)

[5]齐飞，李建文，张舒怡，等.基于LCL滤波器的光伏并网复合控制策略 [J].电机与控制应用，2016，43(1)：48-53.

(QI Fei，LI Jian-wen，ZHANG Shu-yi，et al.Multiple control strategy of grid-connected photovoltaic based on LCL filter [J].Electric Machines & Control Application，2016，43(1)：48-53.)

[6]殷进军，刘邦银，段善旭.LCL滤波并网逆变器双环控制参数设计与优化 [J].电力系统自动化，2013，37(9)：123-128.

(YIN Jin-jun，LIU Bang-yin，DUAN Shan-xu.Parameters design and optimization of dual-loop controller for grid-connected inverters with LCL filters [J].Automation of Electric Power Systems，2013，37(9)：123-128.)

[7]许方玲.三相并网逆变器中LCL滤波器谐振问题研究 [D].秦皇岛：燕山大学，2015：1-78.

(XU Fang-ling.The research of LCL filter resonance problem in three-phase grid-connected inverter [D].Qinghuangdao：Yanshan University，2015：1-78.)

[8]闫一斌，王锦泷.基于 LCL 谐振问题的并网控制策略研究 [J].电气开关，2015，53(6)：19-23.

(YAN Yi-bin，WANG Jin-long.Grid control strategy based on LCL resonant problems [J].Electrical Switch，2015，53(6)：19-23.)

[9]田鹏，宣文华，牛益国.基于陷波控制的LCL型光伏并网逆变器谐波谐振抑制研究 [J].电力系统保护与控制，2016，44(14)：82-88.

(TIAN Peng，XUAN Wen-hua，NIU Yi-guo.Suppression of harmonic resonance for photovoltaic grid-connected inverter with LCL filter based on notch filter control [J].Power System Protection and Control，2016，44(14)：82-88.)

[10]赵艾萍，张峰.叠加定理在电路教学中的妙用 [J].电气电子教学学报，2014(3)：50-52.

(ZHAO Ai-ping，ZHANG Feng.Application of superposition theorem in teaching of circuit [J].Journal of Electrical & Electronic Education，2014(3)：50-52.)

(责任编辑：景 勇 英文审校：尹淑英)

Coupling resonance characteristics of multiple grid-connected inverters

ZHU Xiao-hui1, YUAN Yu-xia1, ZHANG Qing-hui2

(1. School of Electrical Engineering, Zhengzhou University of Science & Technology, Zhengzhou 450064, China; 2. School of Information Science and Engineering, Henan University of Technology, Zhengzhou 450001, China)

In order to solve the complex coupled resonance problem for the parallel grid-connected system of grid-connected inverters with multiple LCL filters, the mathematical model for single inverter was established, which was extended to form the mathematical model for the multiple inverter parallel system. With considering the equivalent circuit model when the inverter itself, parallel inverter and grid separately functioned, a small signal equivalent simplified circuit of multiple inverter parallel system based on the superposition theorem was proposed. With the frequency domain analysis method, the coupling resonance characteristics of multi inverters in parallel were analyzed, which were compared with the resonance characteristics of single inverter. The results show that an additional resonance peak will occur in the multiple inverter parallel system, and the resonance peak value and frequency are related to the number of parallel inverters.

LCL filtering; parallel connection; coupling; resonance; mathematical model; superposition theorem; frequency domain analysis

2016-05-09.

河南省科技攻关计划资助项目(152102210002).

朱小会(1982-)，女，河南郑州人，讲师，硕士，主要从事智能控制系统等方面的研究.

10.7688/j.issn.1000-1646.2017.03.02

TM 615

A

1000-1646(2017)03-0248-05

*本文已于2017-03-28 17∶03在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20170328.1703.020.html