准确把握关键性问题,让数学教学更深刻
——“有趣的一笔画”教学思考与实践
2017-06-06张祖润
◇张祖润

“有趣的一笔画”源自“七桥问题”,也是大学课程《运筹学》中的一个知识点。如何引导小学生认识这样一个由实际问题抽象出的数学问题呢?如果我们仅仅把教学停留在告知学生一笔画图形的判定方法,那就显得过于浅薄了。从核心素养的培育角度看,我们就要思考:一笔画问题的教育价值是什么?指向学生数学核心素养的实质到底是什么?最关键的问题是什么?只有把握住最关键的核心问题,才能在教学中有针对性地展开教学,培育关键能力,提升核心素养。
在教学预设时,笔者对本学习内容在小学阶段的价值进行了分析,感到它至少包含三层意思:1.感受数学抽象。从学习内容看,一笔画问题需要学生把生活问题抽象成数学问题,从图形与图形的关系中抽象出数学概念,从事物的具体背景中抽象出一般规律,并学会用数学语言描述一笔画问题的规律。2.体会数学建模。研究一笔画问题的实质就是让学生对现实的问题进行抽象,经历用数学知识与方法构建模型解决一笔画问题的过程,积累用数学解决实际问题的经验。3.学习研究方法。引导学生经历研究一笔画问题的过程,学习研究此类问题的方法策略,在研究的过程中实现模型的建构,有效达成数学抽象。基于此,我提出了本节课的关键性问题:“怎样有效引导学生经历将一笔画问题抽象成数学模型的过程?”
一、什么是一笔画问题——用基于史实的故事情境引发问题思考
佐藤学认为,课程设计越简单越好,如果要点过多,教师往往只会专注于自己是否完成目标,而忽略学生的反应。据此,我们认为,在把握次关键性问题教学时只要做到“提纲挈领,抓大放小”即可。如何引发学生对一笔画问题进行深度思考呢?如何达到“多快好省”(叶圣陶先生语)?基于高观点背景下的数学体系的认知,直接从数学史的故事情境引入,可以让学生对问题做到先入为主,从而理解一笔画图形的基本概念。
1.故事引入。
谈话:今天我们的数学课要从一则故事说起,18世纪初,东普鲁士的首府哥尼斯堡是一座景色迷人的城市。其中一个公园里有一条河,河上有两个小岛,七座桥把两个岛和河岸连接起来。居民经常沿河过桥散步,于是提出了一个问题:怎样才能不重复、不遗漏地一次走完七座桥,最后又回到出发点呢?这个问题困扰了人们很多年,直到1836年,数学家欧拉经过锲而不舍的研究,终于将七桥问题转化成一笔画问题,才顺利找到答案。
2.课题进入。
揭题:今天我们就要沿着欧拉的脚步,一起来研究有趣的一笔画问题。
提问:你知道什么是一笔画问题吗?谁来介绍一下?请学生上讲台画图说明。
揭示:一笔画是指从图形的某一点出发,笔不离开纸,不间断、不重复地画完一个图形。
3.问题深入。
谈话:是不是所有图形都能一笔画出呢?
判断:(出示图1-图7)谁能一眼看出哪幅图肯定不能一笔画成?为什么?
生:图6肯定不可以。

图1
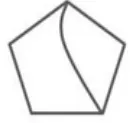
图2
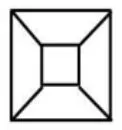
图3
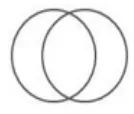
图4

图5

图6
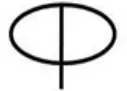
图7
说明:由此可见,能一笔画成的图形必须是相连、相通的,我们叫它——连通图。图6中的两个三角形之间没有相连相通,不是连通图,所以一定不可以一笔画成。
二、一笔画图形与图形的什么有关——用基于操作的观察猜想引发问题探索
儿童对一笔画问题是充满探究的乐趣的,如果直接告诉学生与奇点、偶点的数量有关系,而忽略了学生个体的个性化思考,势必会剥夺学生的观察想象能力和数学思辨能力,削弱探索规律教学的价值,数学核心素养的培育也就无从谈起了。
1.操作感知。
操作感知:剩下的连通图中,是不是都能一笔画成呢?请同学们试着画一画。
汇报交流:哪些图形能一笔画成?学生尝试进行汇报。
分类展示:根据学生的交流情况,进行分类汇总。
2.思考探索。
猜想:在这些连通图中,能一笔画成的图形与图形的什么有关呢?请大家在小组里讨论一下。
小组讨论后进行汇报。
生:我猜想可能与连接点有关,因为由点出发的线的数量有多有少。
生:我认为与点相连的边的数量有多有少,会不会与能否一笔画成有关联?
生:我以前听说过,好像叫什么奇点与偶点。
3.概念揭示。
谈话:你们真会观察,想法和欧拉的发现很相似,欧拉也发现了这些点,他把与奇数条边相连的点叫奇点,与偶数条边相连的点叫偶点。
辨析:你能判断出这两个点分别是什么点吗?哪位同学来介绍一下你的方法?请在图中任意找几个点,同桌相互指一指、说一说。
三、一笔画图形与奇点、偶点有怎样的关系呢——用基于实验的验证方法引发模型建构
“一笔画图形与奇点、偶点有怎样的关系呢?”这个次关键性问题是本节课教学的核心问题,在教学中,不仅要给予学生充分的探究空间,更要引导学生对探究过程进行反思总结,形成清晰的模型建构过程。
1.引发思考:认识了奇点、偶点,那么一个图形能否一笔画成与这些点之间到底有怎样的关系呢?请同学们填一填,看看有什么发现。
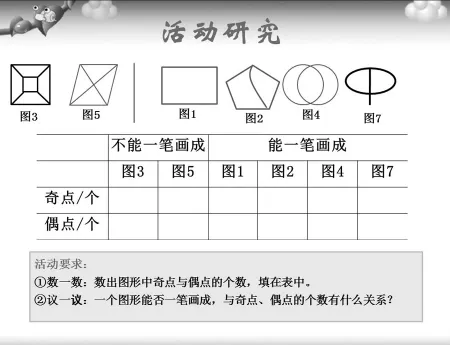
图8
活动要求:
①数一数:数出图形中奇点数与偶点数,填在表中。
②议一议:一个图形能否一笔画成,与奇点、偶点的个数有什么关系?
2.提出猜想:读一读记录的数据,你有什么大胆的猜想?
生:我发现不能一笔画成的图形,奇点的个数是4个或8个。
生:我发现不能一笔画成的图形,偶点的个数是没有规律的。
生:我发现能一笔画成的图形,奇点的个数都是0个或2个,而偶点的个数是不受限制的。
3.实验验证。
引发实验:刚才我们通过研究得出了初步猜想,这个猜想对不对?还要进行验证。
设计实验:我们可以怎样验证猜想?
生:我们可以通过画图举出更多的例子,用实验的方法进行验证。

(表格略)
4.概括结论。
通过实验研究,我们发现能一笔画成的图形,奇点的个数只能是0个或2个,与偶点的个数无关。
5.回顾反思。
提问:刚才我们是怎样研究一笔画图形的特征的?请同学们先自己回顾一下,再和同桌说一说。
生:我们首先要确定这些图形是不是连通图,只有连通图才有可能一笔画成。
生:我们先猜想能否一笔画成的图形可能与什么有关,经过观察、讨论发现可能与点有关。
生:在研究时,我们对能否一笔画成的图形的奇点、偶点的数量进行统计,初步提出了猜想。再用实验的方法进行验证,最后发现了结论。
四、七桥问题的原型是一笔画问题吗——用基于原型的认知建构引发模型应用
一笔画问题教学的本质意义在于引导学生学会一定的研究方法,初步构建基于生活原型的模型,并尝试在生活中进行简单地应用,从而获得科学、合理的模型建构方法与策略。
1.七桥问题。
让我们回到课前的七桥问题,七桥问题的原型是一笔画问题吗?(学生表示不甚理解)欧拉认为:人们关心的只是不重复地一次走遍这七座桥,而并不关心桥的长短和岛的大小。因此,他用4个点分别表示小岛和河岸,用7条线段表示7座桥(出示图9),于是“七桥问题”就转化为一笔画问题。

图9
问题解决:现在你们找到答案了吗?人们可以不重复地一次走遍这七座桥吗?
(生介绍想法和理由)
2.其他实际问题。
(1)根据图形(图略)判断:哪些图形能一笔画成?哪些不能?为什么?
(2)根据生活规划:快递员想不重复地一次走遍这些投放点(如图10),他可以做到吗?该怎样规划行走路线?
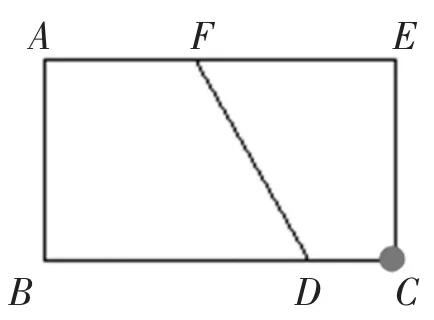
图10
3.模型延伸。
谈话:如果快递员从C点出发,他能不重复地一次走遍这些投放点吗?(不能)明明是可以一笔画成的图形,怎么到这里就不行了呢?看来如何规划行走路线还是有规律可探寻的,同学们课后可以继续去研究。
