基于fsolve的电力系统潮流计算

2017-06-05江宁强黄畅想

电气电子教学学报 2017年1期

关键词：代数方程潮流计算结果

江宁强，黄畅想

(南京理工大学自动化学院电气工程系，江苏南京 210094)

基于fsolve的电力系统潮流计算

江宁强，黄畅想

(南京理工大学自动化学院电气工程系，江苏南京 210094)

潮流计算是本科“电力系统分析”课程的重点内容，也是电力系统相关专业研究生课程的基础。本文采用Matlab中求解代数方程的函数fsolve，提出了潮流计算的一种编程方法。并以包含TCSC的电力系统为例，阐述了计算步骤和程序。所得程序简明清晰，易于扩展修改，可用于“电力系统分析”、“电力系统计算机辅助分析”等课程的教学实践。

电力系统；潮流计算；fsolve

0 引言

潮流计算是“电力系统分析”、“电力系统计算机辅助分析”等电气专业本科课程的重点内容。在教学中往往着重阐述牛顿-拉夫森法潮流计算的原理[1]，但根据该原理直接编写计算程序时，雅可比矩阵的构造较繁琐，代码长且程序不直观，调试工作量大，学生在完成相关计算时易出错。此外，目前的教学内容主要针对传统的交流电力系统，在研究生教学阶段，涉及柔性交流输电(FACTS)、高压直流输电(HVDC)等时，还需仔细修改雅可比矩阵的相关元素，程序的扩充修改较为不便[2，3]。

潮流计算的实质是求解一个非线性代数方程组。为提高编程效率和作业的正确率，本文提出一种基于fsolve函数的潮流计算方法。fsolve是Matlab中的代数方程计算函数，可用于求解线性或非线性方程组。采用该函数进行潮流计算，能够显著减少程序量，提高直观性，并易于扩充和修改。

1 潮流计算中的代数方程组

对于传统的交流电力系统，潮流计算需求解的方程组通常由功率平衡方程构成。若记EPQ为PQ节点集合，EPV为PV节点集合，E0为平衡节点。则PQ和PV节点的有功平衡方程为

(1)

PQ节点的无功平衡方程为

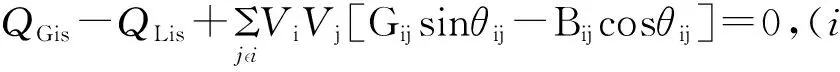
(2)

上述方程中下标s表示已知量。Vi、θi为节点i电压的幅值和相位，PGi、QGi为发电机有功/无功出力，PLi、QLi为有功和无功负荷，Gij、Bij为导纳矩阵中i-j元素的实部和虚部。

潮流计算中首先将式(1)、(2)联立，建立功率平衡方程组；然后计算电压相关未知量；最后确定各支路的消耗功率以及发电机出力等。

考虑FACTS、HVDC时，需补充这些元件在交流节点上的等效负荷，以及其它代数约束方程。以串补设备(TCSC)为例[2]，设电网中PQ节点k(首端)至m(末端)间装设了串补设备，该设备采用恒定有功控制，则需增加一个未知量XTCSC，即串补设备的等值基波电抗。对于这两个节点，式(1)和(2)变为式(3)和(4)。

(3)

(4)

并增加以下代数约束：

PTCSC,k-PTCSC,ks=0

(5)

PTCSC,k-VkVmsin(θk-θm)/XTCSC=0

(6)

QTCSC,k-Vk[Vk-Vmcos(θk-θm)]/XTCSC=0

(7)

PTCSC,m-VmVksin(θm-θk)/XTCSC=0

(8)

QTCSC,m-Vm[Vm-Vkcos(θm-θk)]/XTCSC=0

(9)

式(5)表示稳态时串补设备输送的有功功率为设定值PTCSC,ks，式(6)～(9)用节点电压和XTCSC表示设备在两端节点上的等值有功/无功负荷。

3 基于fsolve的潮流计算

fsolve是Matlab中求解代数方程或代数方程组的函数，可用于求解线性或非线性方程组。对于代数方程组

f(x)=0, (xR″)

(10)

用fsolve求解该方程组的格式为

x= fsolve(@f,x0,options)

(11)

其中f为定义代数方程组的函数文件(.m文件)，x0为初值，options中定义变量的计算精度、函数残值，以及最大迭代次数等终止条件，x为计算结果。此外，options中还提供相应选项，用于显示每次迭代的步长、残值，或结果处的雅可比矩阵。需注意的是，该函数不支持嵌套计算。

式(1)、(2)表示的传统交流网络模型以及式(3)～(9)表示的FACTS系统模型都是非线性方程组，下面讨论采用fsolve进行潮流计算的流程和编程实现方法。计算流程如图1所示，与通常的计算流程相比较，省去了功率失配量、雅可比矩阵、电压修正量计算以及迭代终止条件判别等环节。

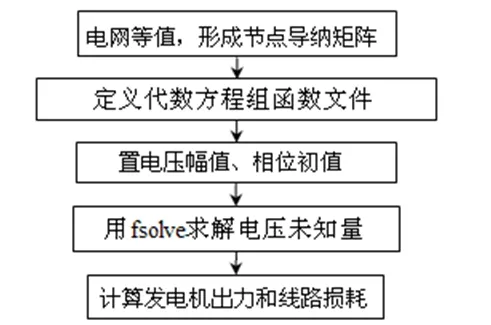
图1 潮流计算流程

以上述的FACTS系统为例，相应的编程实现包括以下步骤：

(1)形成节点导纳矩阵。由节点表N和支路表B生成节点导纳矩阵Y，与传统方法相同，本文不赘述。表N和B可采用多种格式，附录所示为简化的IEEE数据格式。附录中矩阵TCSC为FACTS设备参数。

下列语句由表格获得系统参数，百分号“%”后为注释：

global N ng n Y selp selq TCSC %声明全局变量

n=length(N(:,1)); %节点数

ng=length(find(N(:,2)>1)); %V已知的节点数

selp=find(N(:,2)～=3); %P已知的节点

selq=find(N(:,2)==1); %Q已知的节点

(2)定义代数方程组函数文件。建立描述代数方程组的f.m文件，程序如下：

function y=f(x) %x=[theta,V]global N ng n Y selp selq TCSC %声明全局变量

vabs=N(:,3);vabs(selq)=x(n:n*2-1-ng);%待求幅值the1=N(:,4)/180*pi;the1(selp)=x(1:n-1);%待求相位

y1=[(N(selp,7)-N(selp,5))/100-vabs(selp).*…

(abs(Y(selp,1:end)).*cos(-the1(selp)*…

ones(1,n)+ones(n-1 ,1)*the1′+…

angle(Y(selp,1:end)))*vabs);

%式(1)

(N(selq,8)-N(selq,6))/100+vabs(selq).*…

(abs(Y(selq,1:end)).*sin(-the1(selq)*…

ones(1,n)+ones(n-ng,1)*the1′+…

angle(Y(selq,1:end)))*vabs)];

%式(2)

if ～isempty(TCSC)

%含TCSC时k=TCSC(1); m=TCSC(2); %TCSC首末端节点号

pk=TCSC(6);

%式(5)

vk=vabs(k); thek=the1(k); %首端电压幅值/相位

vm=vabs(m); them=the1(m);%末端电压幅值/相位

Xtcsc=vk*vm*sin(thek-them)/pk;

%式(6)

qk=vk*(vk-vm*cos(thek-them))/Xtcsc;

%式(7)

pm=vm*vk*sin(them-thek)/Xtcsc;

%式(8)

qm=vm*(vm-vk*cos(them-thek))/Xtcsc;

%式(9)

k1=find(selp==k);m1=find(selp==m);

y1(k1)=y1(k1)-pk;y1(m1)=y1(m1)-pm;

%式(3)

k2=find(selq==k);m2=find(selq==m);

y1(n-1+k2)=y1(n-1+k2)-qk;

y1(n-1+m2)=y1(n-1+m2)-qm;

%式(4)end

y=y1;

程序首先定义了传统的潮流计算模型y1，然后得到可考虑TCSC的计算模型y。

(3)设置电压初值，与传统方法相同。

(4)用fsolve计算电压未知量。程序如下：

opt=optimset(′TolFun′,1e-12,’Display’,’iter’);

%设置计算精度，显示fsolve内部迭代过程x=fsolve(@f,[N(selp,4)*pi/180;N(selq,3)],opt);

N(selq,3)=x(n:end);N(selp,4)=x(1:n-1)*180/pi;

u=N(:,3).*exp(N(:,4)/180*pi*1i) %电压计算结果

(5)由节点电压计算各发电机出力和线路损耗，计算方法与传统方法相同。

基于fsolve的潮流计算程序核心在于潮流计算模型的描述，即f.m文件。该文件中保留了模型中代数方程式(1)～(9)的原有形式，具有很强的直观性，清晰易懂，因此编写和调试都比较方便。由于不需要详细构造雅可比矩阵的各个元素，程序量显著减少。步骤(2)～(4)共35条语句，而目前的计算程序常通过循环语句构造雅可比矩阵，不仅程序量会多达80～90条语句，而且特别需要注意变量下标的对应关系，否则很容易出错。

此外，f.m中对传统模型y1附加代数方程得到模型y，就能将潮流计算扩展到含TCSC的电力系统，可见程序易于扩充修改，对复杂电力系统模型有较强的适应性。

4 算例

以一个含TCSC的三机系统为例，系统结构如图2所示，TCSC安装于节点9、10之间[4]。

图2 TCSC三机系统

系统节点数据、支路数据、节点导纳矩阵和TCSC参数见附录中的矩阵N、B、Y和TCSC，功率基准为100 MVA。TCSC采用恒定有功控制，功率设定值为0.65 pu。潮流计算结果见表1。

表1 三机系统潮流计算结果

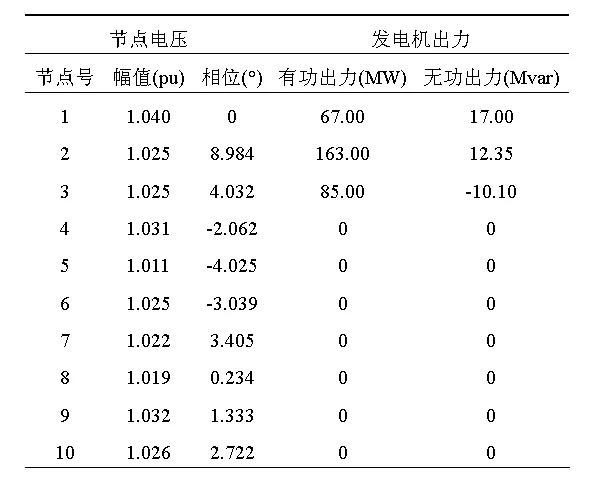
TCSC在节点9和节点10的等效负荷分别为65.00-16.93 i和-65.00+15.26 i。Matlab显示的fsolve内部迭代过程示于表2。

表2 fsolve内部迭代过程

经5次迭代后，x的计算精度达到1e-12，残量减小到1.57994e-28。经校验，计算结果与采用传统编程方法的牛顿-拉夫森法迭代计算结果一致。

5 结语

将fsolve用于电力系统潮流计算，能够摆脱繁琐的雅可比矩阵编程，使计算程序简明直观，便于扩展应用于较复杂的电力系统。在教学过程中结合应用这个新的计算工具，一方面在课堂教学中能够节约课时，更集中于潮流计算模型，即代数方程组构造过程的讲解；另一方面也为学生克服潮流计算中编程的困难提供了有效的途径，有助于提高计算作业的正确率。

[1] P. Kundur. Power System Stability and Control [M], New York: McGraw-Hill, 1994

[2] 王锡凡，现代电力系统分析[M].北京:科学出版社,2003

[3] 徐政.交直流电力系统动态行为分析 [M]. 北京:机械工业出版社,2004

[4] P. Anderson, A. Fouad. Power system stability and control,2nd Ed[M]. New York: Wiley,IEEE Press, 2003

附录节点参数和支路参数

1、节点表

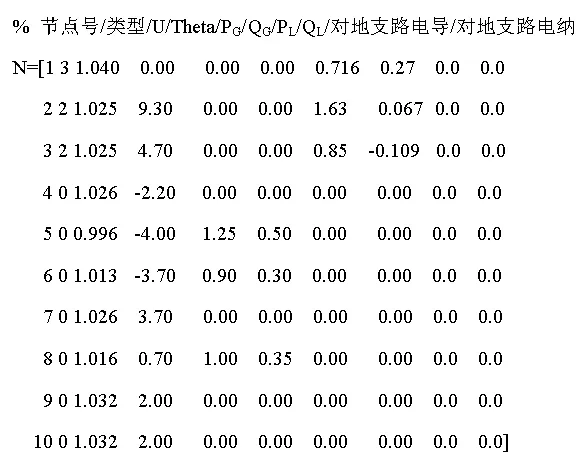
2、支路表

3、节点导纳矩阵

4、TCSC参数表

Fsolve Based Power Flow Calculation

JIANG Ning-qiang, HUANG Chang-xiang

(Dept.Electricalengineering,SchoolofAutomation,NanjingUniversityofScienceandTechnology,Nanjing210094,China)

Power flow calculation is an important part of Power System Analysis course for the undergradute and is the basis for the following graduate courses. A programming method is proposed for power flow calculation which uses the function fsolve in Matlab environment. Taking the power system with TCSC as example, the procedure and program of power flow calculation is clarified. The program is concise and easy to be extended. It can be applied in teaching of Power System Analysis and Power System CAD courses.

power system; power flow; fsolve