整环上的u-算子及其同调特征

李 庆

(西南民族大学 计算机科学与技术学院, 四川 成都 610041)

整环上的u-算子及其同调特征

李 庆

(西南民族大学 计算机科学与技术学院, 四川 成都 610041)

u-算子; UP整环;u-正合列;u-模

1 预备知识

在拟Frobenius环研究中,Faith猜测,即完全的单边自内射环是拟Frobenius环,成为众多学者关注的焦点;由此将内射性进行推广成为众多学者研究的课题,参见文献[1-3].文献[3]引入极大性内射模的概念;文献[4]研究了交换环上的极大性内射模,特别在MFG整环上通过极大性内射模来构造一个星型算子,深入刻画了极大性内射模的性质;文献[5]在文献[4]的基础上将极大性内射模推广到U-内射模并展开了一系列的讨论.本文期望类通过U-内射模建立一个新的星型算子,将乘法理想理论与同调性质结合起来展开对U-内射模较为系统的讨论.

2 自U-内射环

首先回顾文献[5]中的几个重要概念.

定义 2.1[5]设R是交换环,M是R-模,U-Tor(M)={x∈M|存在J∈U,使得Jx=0}，则U-Tor(M)是M的子模,称为M的U-挠子模.若U-Tor(M)=M,称M为U-挠模;若U-Tor(M)=0,称M为U-无挠模.

定义 2.3 设R是交换环,若R作为R-模是U-内射模,则称R为自U-内射环.若环R中的理想作为R-模是U-内射模,称该理想为U-内射理想.

定理 2.4 设R是U-无挠的自U-内射环,则以下各条等价:

1) M是U-无挠模;

2) 对任何x∈M,annR(x)是R的U-内射理想;

3) 对任何X⊆M,annR(X)是R的U-内射理想.

证明 1)⟹2) 设J∈U,a∈R,Ja⊆annR(x),故Jax=0.因M是U-无挠模,则ax=0.故a∈annR(x).由文献[5]的定理3.4,annR(x)是U-内射模.

2)⟹3) 因ann(X)=∩{ann(x)|x∈X},由文献[5]的推论3.5,ann(X)是U-内射模.

3)⟹1) 设x∈M,Jx=0,其中J∈U,故J⊆ann(x).因R是U-内射模,故由文献[5]的定理3.4,1∈ann(x).故x=0.因此,M是U-无挠模.

由文献[5]的定理3.9易得出以下结论.

命题 2.5 设R是U-无挠的自U-内射环,M是R-模,则对偶模M*和二次对偶模M**都是U-无挠的U-内射模.从而自反模是U-无挠的U-内射模.

命题 2.6 设R是U-无挠的自U-内射环,则R的非极大的素w-理想都是U-内射理想.

证明 设P是R的非极大的素w-理想,故对任意的J∈U,JP.若x∈R,Jx⊆P,故x∈P.由文献[5]的定理3.4,P是U-内射理想.

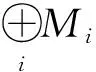
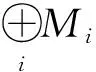
为方便叙述,说R满足(P),是指任意J∈U至少包含一个有限生成子理想I∈U.

命题 2.9 设R是交换环,M是R-模,则有以下结论:

1)M⊆Mu;

2)M是U-内射模当且仅当M=Mu;

3) 如果A是R-模且A⊆M,则Au⊆Mu;

4) 若N是U-内射模,M⊆N,则Mu⊆N;

5) 若R满足(P),则有

i) 设I是R的理想,有(IM)u=(IuMu)u;

ii) (Mu)u=Mu;

iii)Mu是U-内射模.

证明 1)、3)都是基本验证,此处不再赘述.

2)由文献[5]的定理3.4易得结论.

4)设x∈Mu⊆E(M)⊆E(N),存在J∈U使得Jx⊆M⊆N.故x∈Nu.因N是U-内射模,故N=Nu.所以x∈N.故Mu⊆N.

5)i)因IM⊆IuMu,故(IM)u⊆(IuMu)u.反过来,设x∈(IuMu)u,存在J∈U使得Jx⊆IuMu.由R满足(P),故存在有限生成I⊆J,I∈U使得Ix⊆IuMu.故存在J′∈U使得J′x⊆IM,于是x∈(IM)u.

5)ii)显然,Mu⊆(Mu)u.反过来,设x∈(Mu)u,存在J∈U使得Jx⊆Mu.由R满足(P),故存在有限生成I⊆J,I∈U使得Ix⊆Mu.故存在J′∈U使得J′x⊆M,于是x∈=Mu.

5)iii)由2)和5)中的ii)可得结论.

命题 2.10 设R是交换环,M是R-模,a∈R.

1)aMu⊆(aM)u;

2) 若a不是M的零因子,R满足(P),则aMu=(aM)u.

证明 1)设任意x∈Mu,则存在J∈U使得Jx⊆M,从而Jax⊆aM,故ax∈(aM)u.

2)容易知道a不是Mu的零因子.由aMu≅Mu,由命题2.9,aMu是U-内射模,即aMu=(aMu)u.由aM⊆aMu,故(aM)u⊆aMu.再由1)可得(aM)u=(aM)u.

推论 2.11 设R是交换环,I是R的理想,R满足(P),a∈T(R)(这里T(R)为交换环R的完全分式环),则aIu⊆(aI)u.

推论 2.12 设R是整环,R满足(P),I是R的理想,0≠a∈K,则aIu=(aI)u.

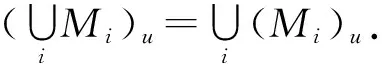
熟知的w-全局变换环Rwg={x∈qf(R)|Jx⊆R,其中J∈U}实际上就是整环R的U-包络,Rwg=Ru.一般情况下,R≠Ru,因此,一般情况下R不是U-内射R-模.由命题2.9可知,当交换环R满足(P)时,u-算子就是半星算子.进一步,当R是满足(P)的自U-内射环时,u-算子就是一类星型算子.期望利用发展较成熟的星型算子工具来研究U-内射模.因此,下面主要对满足(P)的自U-内射整环R上的u-算子和u-模展开一系列的讨论.

3 UP整环上的u-算子

定义 3.1 设R是U-无挠的自U-内射整环，且R满足(P)，则称R是UP整环.

引理 3.2 设R是交换环,对任何U-无挠模M,Mu/M是U-挠模.

定理 3.3 设M是R-模,则以下各条等价:

1)M是U-挠模；

证明 1)⟹2) 不妨记ker(g)=A,由命题2.9,AU⊆B.设任意的x∈B,g(x)∈M.由M是U-挠模,故存在J∈U使得Jg(x)=g(Jx)=0.故Jx∈ker(g)=A,从而x∈Au.

3)⟹1) 由引理 3.2,M≅F/A=Au/A是U-挠模.

定理 3.4 设M是R-模,则以下各条等价:

1)M是U-内射模;

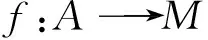
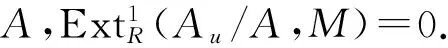
3)⟹4) 由引理3.2易得结论.

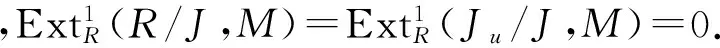
命题 3.5 1) 若J∈U,J是有限生成的,则J∈GV(R);

2)GV-无挠模是U-无挠模;

3)w-模是u-模.

证明 1)因R是自U-内射模,且J∈U是有限生成的,故由文献[5]的定理3.4有HomR(J,R)≅R.因此J∈GV(R)；

2)设M是GV-无挠模,x∈M,J∈U,有Jx=0.故存在J的有限生成子理想I∈U且由1),有I∈GV(R).因M是GV-无挠模,故由Ix=0可推出x=0；

3)由1)和文献[5]的定理3.4易得结论.

命题 3.6 1)R中的极大u-理想是素理想;

2) 设I是R的u-理想,则存在R的极大u-理想P使得I⊆P.

证明 1)设P是R的极大u-理想,a,b∈R,ab∈P,且(a)P,从而(P+Ra)u=R.故b∈Rb=b(P+Ra)u=(b(P+Ra))u⊆Pu=p.故P是素理想.

2)设Γ={A|A是R的u-理想且I⊆A}.由于I是R的u-理想,所以Γ非空.由Zorn引理,Γ中有极大元P.容易知道P就是R的极大u-理想.

命题 3.7R-模M是U-挠模当且仅当对R的任何极大u-理想m,Mm=0.

反过来,令T=U-Tor(M),N=M/T，则N是U-无挠模.任取x∈N,由定理2.4,ann(x)是u-理想.对任何极大u-理想m,由已知条件Nm=0.故存在s∈Rm,使得sx=0.故s∈ann(x).故ann(x)m.从而ann(x)=R.因此,x=0.故N=0,即M是U-挠模.

命题 3.8 设p是R的素u-理想,M是U-无挠模.则Mp=(Mu)p.

证明 由引理3.2,Mu/M是U-挠模.由命题3.7,(Mu/M)p=0.故Mp=(Mu)p.

命题 3.9 设M是U-无挠模,A,B是M的子模.则Au=Bu当且仅当对R的任何极大u-理想m,有Am=Bm.从而若A、B是M的u-子模,则A=B当且仅当对R的任何极大u-理想m,有Am=Bm.

证明 设Au=Bu,故由命题 3.8,Am=(Au)m=(Bu)m=Bm.

反过来,设对R的任何极大u-理想m,有Am=Bm.设x∈Au.令I=(Bu∶x)={r∈R|rx∈Bu}.任取y∈Iu,则存在J∈U,使得Jy⊆I,故Jyx⊆Bu.因此,存在J′∈U,使得J′Jyx⊆B.故yx∈Bu.从而y∈I.故I=Iu.故I是R的u-理想.由于对任何极大u-理想m,有(Bu)m=Bm=Am=(Au)m.从而有Im=(Bu∶x)m=((Bu)m∶xRm)=((Au)m∶xRm)=Rm,其中最后一个等号是因为x∈Au,故xRm⊆(Au)m.因此对R的一切极大u-理想m,Im.又因I是R的u-理想,故I=R,从而x∈Bu.故Au⊆Bu.同理,Bu⊆Au.因此,Au=Bu.

命题 3.10 设p是R的素u-理想,N是Rp-模，则N作为R-模是u-模.

证明 设J∈U,x∈N,Jx=0.因Jp,故可以选择s∈Jp,有sx=0.因N作为R-模,根据其模的构造方式,有x.又因在Rp中是单位,故x=0.从而N是U-无挠模.设J∈U,x∈E(N),Jx⊆N.同上述一样,选择s∈Jp,有sx∈N.因在Rp中是单位,与上述同理,有x∈N.故N作为R-模是u-模.

命题 3.11 设N是U-无挠模,B是任何R-模,

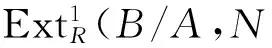
2) 设N是u-模,A是B的子模.若B/A是U-挠模,则HomR(A,N)=HomR(B,N).特别,若A是U-挠模,则HomR(A,N)=HomR(Au,N).

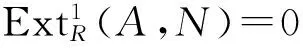
特别,把B替换成Au,同理有HomR(A,N)=HomR(Au,N).

4 UP整环上的u-正合列

1) f可以唯一扩张为Au到Bu的同态;

2)若x∈Au,g(x)=0,则存在J∈U,使得Jx⊆A.故f(Jx)=g(Jx)=Jg(x)=0.因f是u-同构,故fm是单同态,从而Jx=0.又因A是U-无挠模,故x=0.故g是单同态.

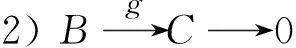
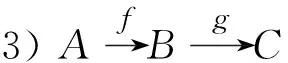
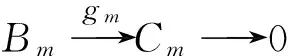
3)知道

((im(f)+ker(g))/im(f))m=(im(f)m+ker(g)m)/im(f)m=(im(fm)+ker(gm))/im(fm),

((im(f)+ker(g))/ker(g))m=(im(f)m+ker(g)m)/ker(g)m=(im(fm)m+ker(gm))/ker(gm),

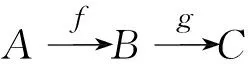
引理 4.6 (u-算子下的广义5引理)设下图是两行都是u-正合列的交换图.

则有：

1) 若α,γ是u-单同态,且δ是u-满同态,则β是u-单同态;

2) 若α,γ是u-满同态,且τ是u-单同态,则β是u-满同态.

特别地,若δ,α,γ,τ都是u-同构,则β是u-同构.

证明 对极大u-理想作局部化即证.

是正合列.

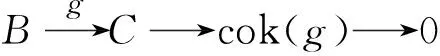
是正合列,故

致谢 西南民族大学中央高校基本科研业务费专项资金(2015NZYQN69)对本文给予了资助,谨致谢意.

[1] 徐龙玉,宋晖. 关于fann-内射模[J]. 四川师范大学学报(自然科学版),2008,32(4):443-446.

[2] 赵国,汪明义. 关于极大内射性的注记[J]. 四川大学学报(自然科学版),2005,21(1):1451-1458.

[3]WANGMY,ZHAOG.Onmaximalinjective[J].ActaMathematicalSinica,2005,21(1):1451-1458.

[4] 王芳贵,汪明义,杨立英. 交换环上的极大性内射模[J]. 四川师范大学学报(自然科学版),2010,33(3):277-285.

[5] 李庆,杨军,李高平，等. 交换环上的U-内射模[J]. 四川师范大学学报(自然科学版),2016,39(2):168-173.

[6]YINHY,WANGFG,ZHUXS,etal. w-modulesovercommutativerings[J].JKoreanMathSoc,2011,48(1):207-222.

[7] 王芳贵. 交换环与星型算子理论[M]. 北京:科学出版社,2006.

[8] 王芳贵,张俊. w-Noether环上的内射模[J]. 数学学报,2010,53(6):1119-1130.

[9]ZHANGJ,WANGFG,KIMH.Injectivemodulesoverw-Noetherianrings,II[J].JKoreanMathSoc,2013,50(5):1051-1066.

[10]KALANSKYI.CommutativeRing[M].Chicago:UnivChicagoPress,1974.

[11]WANGFG. w-modulesoveraPVMD[C]//HongKong:proceedingsoftheISTAEM,2001.

[12]ROTMANJJ.AnIntroductiontoHomologicalAlgebra[M]. 2nd.NewYork:Springer-Verlag,1988.

[13]KIMH,KIMES,PARKYS.InjectivemodulesoverstrongMoridomains[J].HoustJMath,2008,34:349-360.

[14]WANGFG.Onw-projectivemodulesandw-flatmodules[J].AlgebraColloq,1997,4(1):111-120.

[15]WANGFG,MCCASLANDRL.Onstrongmoridomains[J].JPureApplAlgebra,1999,135(2):155-165.

[16]WANGFG,KIMH. w-injectivemodulesandw-semi-hereditaryrings[J].JKoreanMathSoc,2014,51(3):509-525.

2010 MSC：13G05; 13C11; 13D07

(编辑 陶志宁)

u-Operation over an Integral Domain and Its Homological Characterizations

LI Qing

(SchoolofComputerScienceandTechnology,SouthwestUniversityforNationalities,Chengdu610041,Sichuan)

We define an UP domain，u-operation and u-modules by using U-injective modules．We prove that，over an UP-domain， M is U-torsion if and only if for each exact sequence 0 →A →B → g M →0，where B is a U-injective module，Au =B holds． We also prove that M is a U-injective module if and only if a morphism f: A →M can be extended to Au，if and only if for each U-torsion module C，Ext1 R( C，M) = 0． Moreover，we give the definition of u-exact sequences over a UP-domain and prove that A → f B → g C is a u-exact sequence if and only if both( im( f) +ker( g) ) /im( f) and ( im( f) +ker( g) ) /ker( g) are U-torsion modules．Finally，we show that over a UP-domain，if A → f B → g C →0 is a u-exact sequence and N is a u-module，then 0 →HomR( C，N) →HomR( B，N) → HomR( A，N) is an exact sequence．

u-operation; UP-domain;u-exact sequence;u-module

2017-01-04

国家自然科学基金(11401493)和四川省教育厅自然科学重点基金(14ZB0463)

李 庆(1980—),女,副教授,主要从事交换代数、同调代数与代数K-理论的研究,E-mail:lqop80@163.com.

O153.3; O154.2

A

1001-8395(2017)03-0301-07

10.3969/j.issn.1001-8395.2017.03.004