浅析初中数学常见思想方法在教学中的渗透

江苏省苏州市吴江区实验初级中学(215200)

袁孝珍●



浅析初中数学常见思想方法在教学中的渗透

江苏省苏州市吴江区实验初级中学(215200)

袁孝珍●

数学思想是指人们对数学理论和内容的本质的认识，数学方法是数学思想的具体化形式，实际上两者的本质是相同的，差别只是站在不同的角度看问题.通常混称为“数学思想方法”.常见的数学四大思想为: 分类讨论、转化与化归、数形结合、函数与方程.本文讲述这几种初中数学常见的思想方法.

初中数学；思想方法；分析问题；解决问题.

几千年前老子曾说过：“授人以鱼，不如授之以渔.”对于这个道理，所有的教育工作者都有共识，但现实生活中我们更多的是给予学生“鱼”——灌输大量的知识.而我们的目的是让学生懂得怎样学, 怎样把繁杂的问题一一弄清楚.那么在这一过程中，正确的指导思想和方法就起着关键的作用.

下面例析初中数学常见的几种思想方法在解题中的应用.

一、分类讨论

分类讨论就是按照一定的标准，把研究对象分成为数不多的几个部分或几种情况，然后逐个加以解决，最后予以总结作出结论的思想方法.其实质是化整为零，各个击破，化大难为小难的策略.

分类讨论要有原则，主要体现在以下几个方面:

1.有统一标准.

2.要逐类讨论.

3.要不重不漏.

例如：若已知等腰△ABC中，∠A=40°，则∠B的度数为____.

分析：本题分类标准不难找到，应该是按角对等腰三角形分类.那么已知∠A=40°有两种可能(1)顶角；(2)底角.而要求的∠B也有两种可能：(1)顶角；(2)底角.

∠A是顶角⟹∠B是底角⟹∠B=70°;

故本题的答案为70°或40°或100°.

分类讨论思想能够提高学生的数学解题能力，促使学生全面而周密地分析和思考问题，促进并提升思维的逻辑性和严谨性，有效克服思维的片面性.

二、转化化归

转化化归思想是指把一个新问题或复杂的问题通过转化，变为一个已知的或几个简单的问题，从而得到解决的一种思想方法.如下图所示：

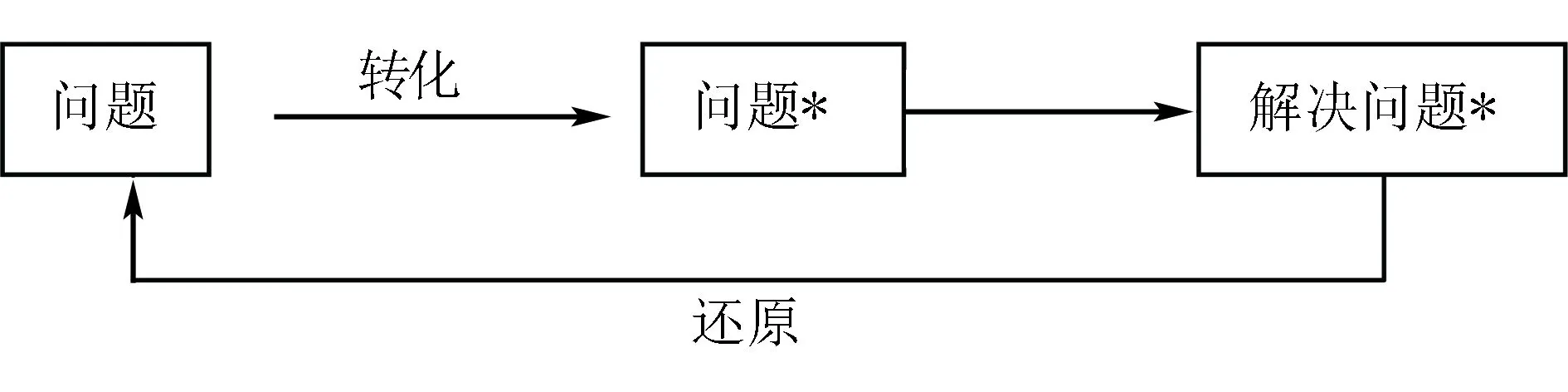
这种思想方法在初中代数、几何中大量地渗透着，一般表现为新知识向旧知识的转化、一般情况向特殊情况的转化等等.

例如：在探讨抛物线y=ax2+bx+c(a≠0)的图象与x轴的交点个数时，根据已经学过的一次函数图象与x轴交点坐标求法，先把二次函数转化为学过的一元二次方程得：ax2+bx+c=0(a≠0)，再根据一元二次根的判别式可知该方程解的个数，还原即得到抛物线与x轴的交点个数.

化归思想对提高学生的思维能力和综合素养，灵活实现知识之间的迁移是非常有帮助的.

三、数形结合

我国著名数学家华罗庚曾说过:“数形结合百般好，隔裂分家万事休.”“数”与“形”反映了事物两个方面的属性.数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来，通过“以形助数”或“以数解形”即通过抽象思维与形象思维的结合，可以使复杂问题简单化，抽象问题具体化，从而起到优化解题途径的目的.

分析：本题从已知条件来看，所求式子中a、b均为变量，直接从“数”的角度去考虑显然有点无从下手.从被开方数观察，都是两数的平方和，因此我们联想到勾股定理，进而可以构造如下图形：

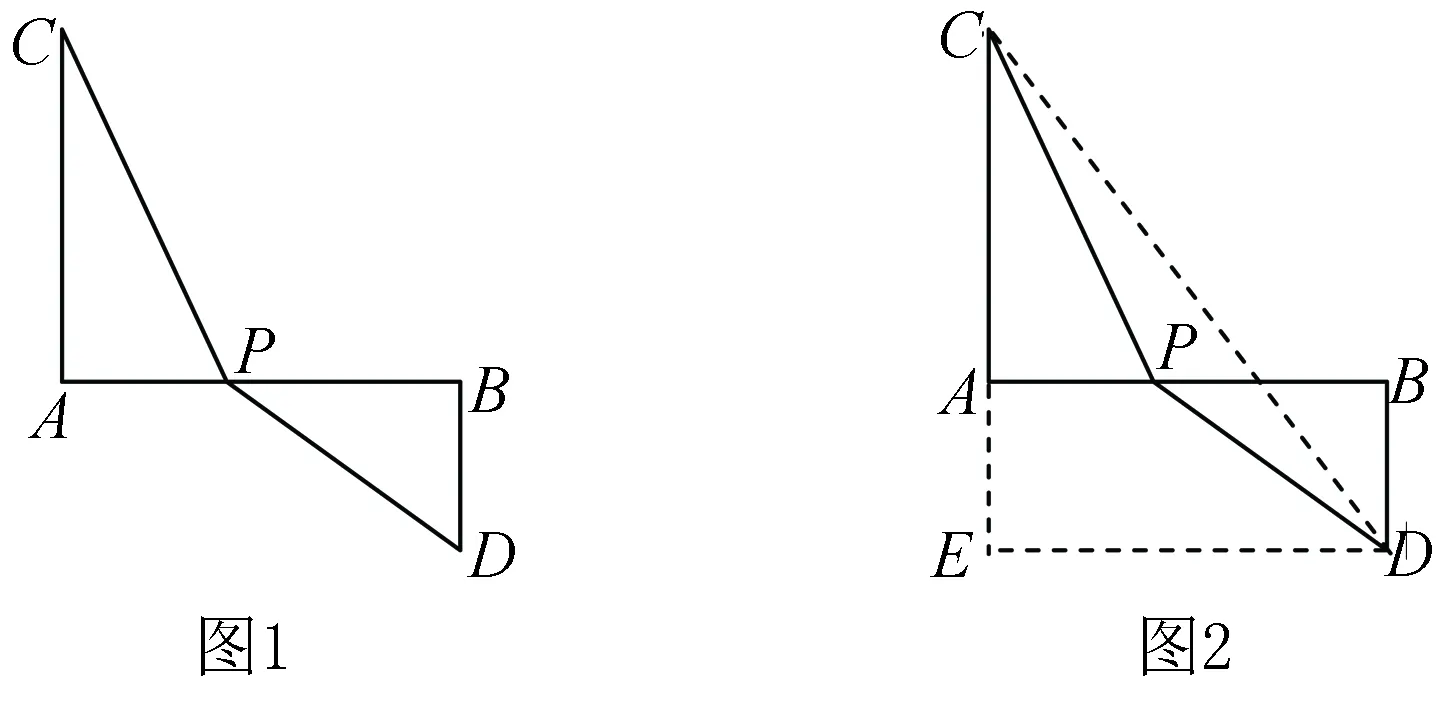
▶◀教师在教学过程中，要引导学生灵活地根据问题的特点和需要，由数思形，以形助数，适时转化，相互作用，使学生解题思路开阔，解题敏捷.

四、函数方程

函数与方程思想是指在解决数学问题的过程中，根据问题中的数量关系，构造出相应的函数或方程，运用函数与方程的知识解决相关问题.

例如：小明从家骑自行车出发，沿一条直路到相距2400 m的邮局办事，小明出发的同时，他的爸爸以96 m/min速度从邮局同一条道路步行回家，小明在邮局停留2 min后沿原路以原速返回，设他们出发后经过tmin时，小明与家之间的距离为s1m，小明爸爸与家之间的距离为s2m，图中折线OABD、线段EF分别表示s1、s2与t之间的函数关系的图象.

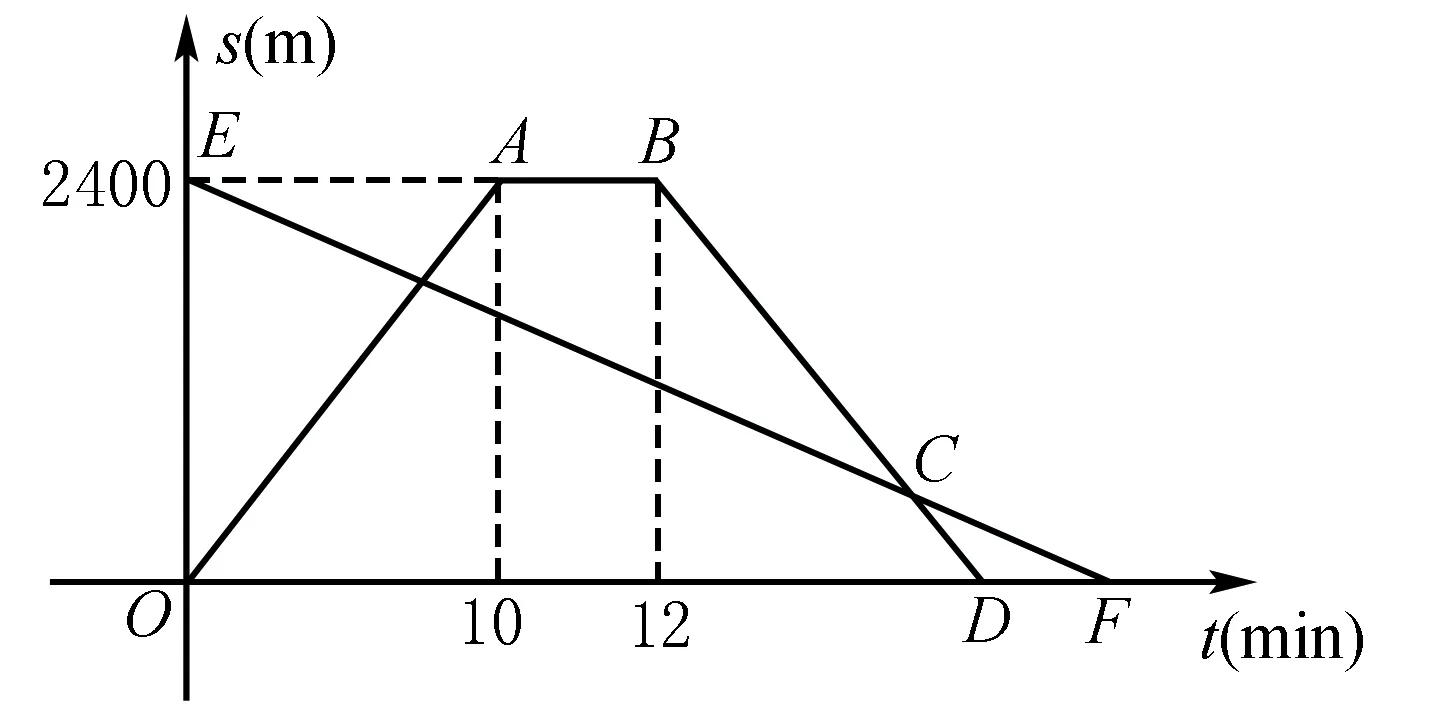
(1)求s2与t之间的函数关系式；

(2)小明从家出发，经过多长时间在返回途中追上爸爸？这时他们距离家还有多远？

分析 本题中的第(1)小题可先根据条件求出爸爸返回所需的时间，得出点F的坐标，再由E、F两点坐标，用待定系数法求出解析式即可.第(2)小题中小明在返回途中追上爸爸的时间可理解成图中点C的横坐标，此时s1=s2，实现函数到方程的转化，求出t的值，代入s1或s2即可求出此时距家的距离.

解 (1)由已知得：爸爸返回共需2400÷96=25(min)，∴F(25,0)，又E(0，2400).

∴s2=-96t+2400(0≤t≤25).

(2)由已知得：

小明整个过程耗时10+2+10=22(min),

∴D(22,0).

设线段BD：s1=k1t+b1，得：

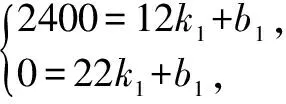
∴s1=-240t+5280(12≤t≤22).

当两人相遇时，s1=s2，即-240t+5280=-96t+2400，

解得:t=20，此时，s1=-240t+5280=480.

故小明从家出发20min钟后在返回途中遇到爸爸，此时距家480m.

方程函数思想是初中数学的核心内容，也是打好数学基础的关键.这两者在解题过程中经常是相辅相成、共同作用，促进了人们对数学知识的深入了解和掌握.在教学过程中，教师要引导学生领会函数跟方程之间的这种关系，能综合运用函数方程思想，熟练并巧妙地进行转化，一步步地解决问题.

初中数学蕴含着丰富的数学思想和方法，我们在教学过程中要教会学生把基本数学思想、方法、知识、技能融于一体，有计划、有目的、有组织地上好思想方法训练课，培养和提高学生的数学素养和解题技能.只有授之以“渔”，才能让学生受用一生.

[1]赵万智.浅谈初中数学教学中几种常见的思想方法[J].教育革新,2008(12)

[2]衡玉树.初中数学中常见的数学思想方法探究[J].中国科教创新导刊,2012(36)

[3]王明碧.初中数学教学中常见的数学思想方法[J].中小学数学(初中版),2010(03)

[4]王威娟.几种常见的初中数学思想方法[J].科普童话,2015(41)

G632

B

1008-0333(2017)14-0018-02