Existence of Positive Solutions for Eigenvalue Problems of Fourth-order Elastic Beam Equations
2017-06-05LUHaixia
LU Hai-xia
(School of Arts and Science,Suqian College,Suqian 223800,China)
Existence of Positive Solutions for Eigenvalue Problems of Fourth-order Elastic Beam Equations
LU Hai-xia
(School of Arts and Science,Suqian College,Suqian 223800,China)
In this paper,we investigate the positive solutions of fourth-order elastic beam equations with both end-points simply supported.By using the approximation theorem of completely continuous operators and the global bifurcation techniques,we obtain the existence of positive solutions of elastic beam equations under some conditions concerning the first eigenvalues corresponding to the relevant linear operators,when the nonlinear term is non-singular or singular,and allowed to change sign.
elastic beam equations;singular;positive solutions;global bifurcation
§1.Introduction and Preliminaries
In this paper,we consider the existence of positive solutions of the following fourth-order two-point boundary value problem

where λ is a positive parameter,f:[0,1]×R1→R1is continuous and may be singular at t=0,1.
Fourth-order two-point boundary value problems are useful for material mechanics because the problems usually characterize the deflection of an elastic beam.In mechanics,the problem (1.1)describes the deflection of an elastic beam with both end-points simply supported.The existence of positive solutions for the elastic beam equations has been studied extensively,see for example[19]and references therein,when the nonlinear term satisfies
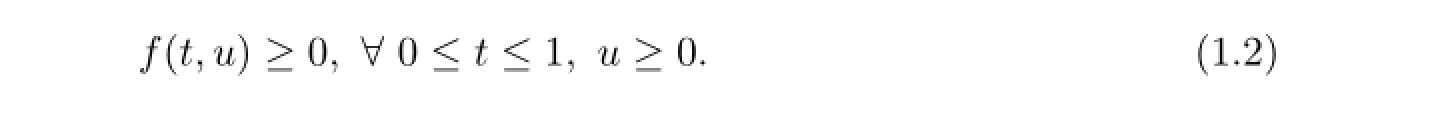
And the major methods used are upper and lower solution method,contraction mapping and iterative technique,Guo-Krasnosel’skii fixed point theorem of cone expansion-compression type, topological degree theory and global bifurcation technique.However,when(1.2)is not satisfied, which means the nonlinear term is allowed to change sign,there are only a few papers concerned with the fourth-order boundary value problems.Yao[10]considered the existence of positive solutions of elastic beam equations by constructing control functions and a special cone and using fixed point theorem of cone expansion-compression type.Lu[11]obtained the existence of positive solutions by the topological degree and fixed point theory of nonlinear operator on lattice.
In this paper,by using the approximation theorem of completely continuous operators and the global bifurcation techniques,we study the existence of positive solutions of the problem (1.1)under some conditions concerning the first eigenvalues corresponding to the relevant linear operators,when the nonlinear term f is non-singular or singular and in the case that(1.2)is not satisfied.The method and results in this paper improve those in[10-11].
For the remainder of this section,we present some definitions and lemmas which are used in Section 2 and Section 3.
Let E be a Banach space,P be a cone of E.
Definition 1.1[12-13]Let B:E→E be a linear operator.B is said to be a u0-bounded operator,if there exists u0∈P{θ},such that for any x∈P{θ},there exist a natural number n and real numbers ζ,η>0,such that

Lemma 1.1[12-13]Let B be a completely continuous u0-bounded operator,λ1>0 be the first eigenvalue of B,then B must have a positive eigenfunction∈P{θ},corresponding to λ1, and λ1is the unique positive eigenvalue of B corresponding to positive eigenfunction.
Lemma 1.2[14]Let B be a completely continuous u0-bounded operator,A:E→E be an operator(we don’t suppose A maps P to P).If there exist ϕ0∈P{θ}and λ>0 such that Aϕ0>Bϕ0,λAϕ0=ϕ0,then λ<λ1,where λ1>0 is the first eigenvalue of B.
Let X be a Banach space and{Cn|n=1,2,···}be a family of connected subsets of X, we define

Lemma 1.3[14]Suppose that the following conditions are satisfied
(1)There exist zn∈Cn(n=1,2,···)and z∗∈X,such that zn→z∗;
(2)rn→+∞(n→∞),where rn=sup{‖x‖|x∈Cn};
Then there must exist an unbounded connected component C in D and z∗∈C.
§2.Existence of Positive Solutions in the Case That f is Not Singular

In this section we consider the boundary value problem(1.1)in the case that f is not singular and f(t,u)=a(t)u+F(t,u).
We assume that
(H1)a∈C[0,1]with a(t)≥0 on[0,1]and a(t)/≡0 on any subinterval of[0,1];

(H3)There exists α∈(-∞,+∞),such that
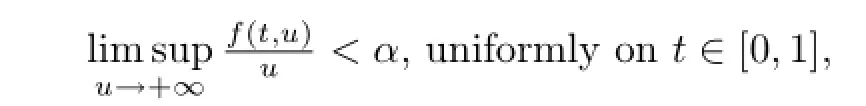
where it is not supposed that f(t,u)≥0(u≥0).
Let

It is easy to verify that G(t,s)is nonnegative continuous and for t,s∈[0,1]×[0,1],

It is obvious that(1.1)can be converted to the following integral equation

It is easy to see that A:C[0,1]→C[0,1]is a completely continuous operator.Evidently,the fixed point of λA is the solution of(1.1).
We see from(H2)that the linearization of the boundary value problem(1.1)is

By Theorem 2.3 in Ma[15],we have
Lemma 2.1Suppose(H1),(H2)are satisfied.Then
(1)Problem(2.3)has an infinite sequence of positive eigenvalues

(2)To each eigenvalue λkthe algebraic is 1 and there corresponds an essential eigenfunction ϕkwhich has exactly k-1 simple zero in(0,1)and is positive near 0.
Let

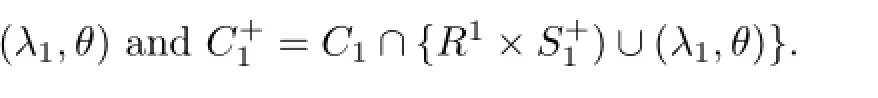
By Rabinowitz[16],Lemma 2 in Sun[17]and Lemma 2.1 we know that
Lemma 2.2Suppose(H1),(H2)are satisfied,then C+1is an unbounded connected component of((0,+∞)×S+1)∪{(λ1,θ)}in R1×C[0,1].
Define the linear operator
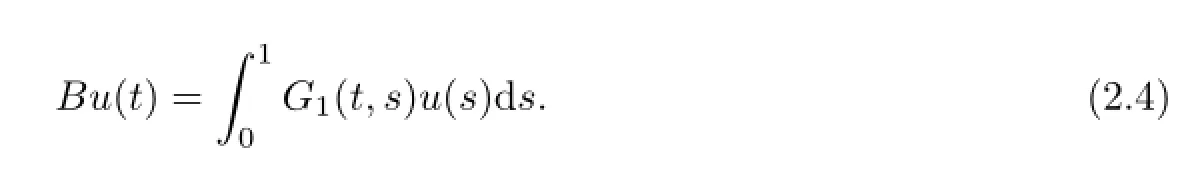
Lemma 2.3Operator B defined by(2.4)is a u0-bounded operator.


Let u0(t)=P(t),t∈[0,1].For any u∈P{θ},we have

which means the linear operator B is u0-bounded operator.
Let r(B)and λBdenote the spectral radius and the first eigenvalue of B respectively,then λB=(r(B))−1.



By(H3),there exists M0>0 such that



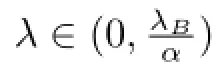
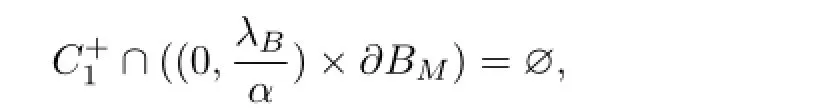


Theorem 2.2Suppose that(H1)~(H3)hold and α≤0 in(H3),then for any λ∈(λ1,+∞),the boundary value problem(1.1)has at least a positive solution.
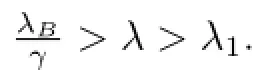
§3.Existence of Positive Solutions in the Case That f is Singular
In this section we consider the boundary value problem(1.1)in the case that f(t,u)= h(t)g(u)and h is allowed to be singular at t=0 or t=1.i.e.,
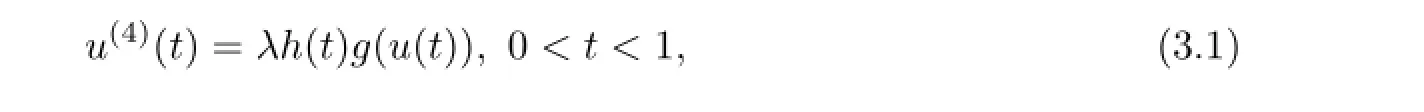

We assume that
Define nonlinear operator A and linear operator B
Then the fixed point of λA is the solution of(3.1)~(3.2).
For any natural number n(n≥2),we set

Then hn:[0,1]→[0,+∞)is continuous and hn(t)≤h(t),t∈(0,1).Let

then An,Bn:C[0,1]→C[0,1]are continuous.And the boundary value problem(3.5),(3.2)and (3.6),(3.2)can be converted into the following nonlinear integral equation and linear integral equation u(t)=λAnu(t)and u(t)=λBnu(t),respectively.


Then we have the following lemma.

Similarly,B:C[0,1]→C[0,1]is completely continuous.
Lemma 3.2Suppose that(H′3)is satisfied,then operators B and Bndefined by(3.3)and (3.7)are u0-bounded operators.
ProofBy(2.2)and(H′3)and by the same method as the proof of Lemma 2.3,we know that Lemma 3.2 holds.
Let λ1and λ1n(n=2,3,···)denote the first eigenvalue of u0-bounded linear operators B and Bnrespectively,then λ1>0 and λ1n>0 and λ1=(r(B))−1,λ1n=(r(Bn))−1(n= 2,3,···),where(r(B))−1and(r(Bn))−1denote the spectral radius of linear operators B and Bnrespectively.




(i)D is the subset of the solution of the boundary value problem(3.1),(3.2)and
For any(λ,u)∈D,it follows the definition of D that there exist the subsequence{nk}⊂{n} and(λnk,unk)∈C+1nk,such that λnk→λ,unk→u.Thus{λnk}and{unk}are bounded.And by the proof of Lemma 3.1 we know Anuniformly converges to A on a bounded set.So
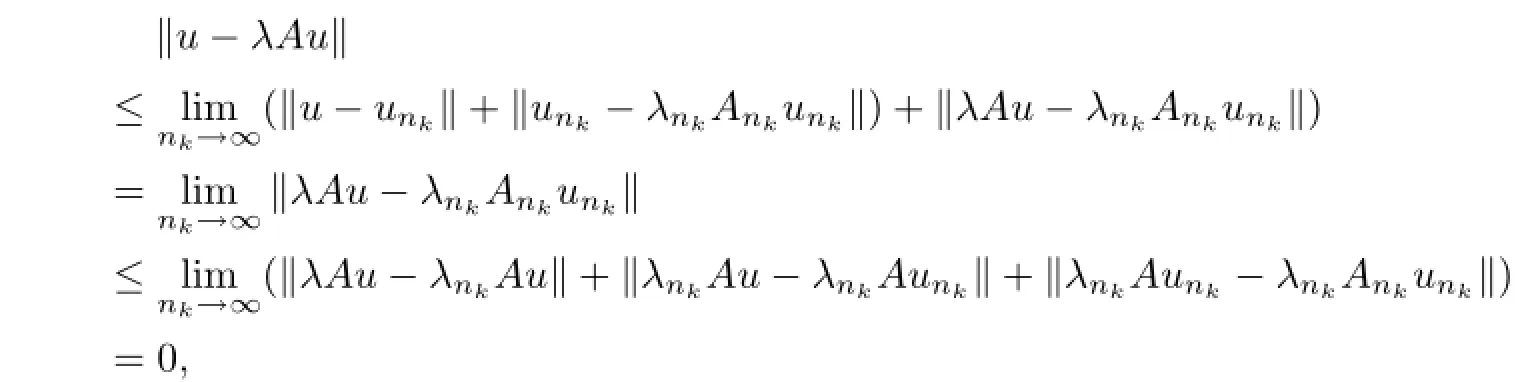
which means u=λAu.So(i)holds.
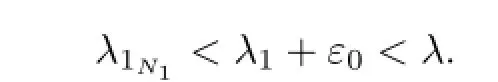


If(3.8)does not hold,then for any δ1:0<δ1<δ,there exist λ>λ1+ε0,u∈K and N2>N1, such that u=λAN2u,0<‖u‖<δ1.By(3.9)we have
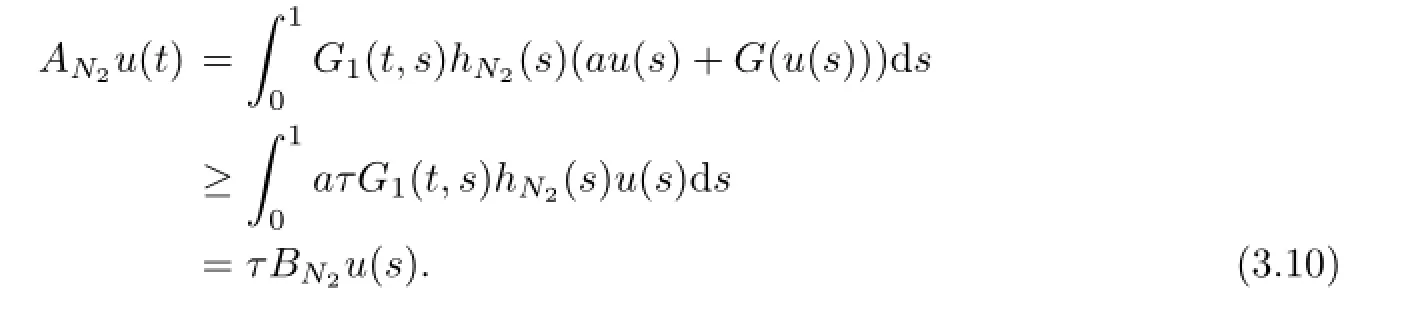
It follows from Lemma 3.2 τBN1,τBN2are u0-bounded linear operators.Let τ−1λ1N1and τ−1λ1N2be the first eigenvalue of τBN1and τBN2respectively.From(3.10)and Lemma 1.2 we know that λ<τ−1λ1N2.Since hN2≥hN1,then τBN2≥τBN1and so τ−1λ1N2≤τ−1λ1N1. Then

which is a contradiction.Thus(3.8)holds.
By(3.8)and the definition of D,we know that(ii)holds.
It follows from Lemma 3.3 that(λ1n,θ)→(λ1,θ).Note that for any n≥2,C+1nis unbounded.Hence,by Lemma 1.3 there exists an unbounded connected component C in D, containing(λ1,θ).From the property(ii)of D we have

By(3.11)and the same method as the proof of Theorem 2.1,we have

which means Theorem 3.1 holds.
It follows from the same method as the proof of Theorem 2.2,we have
Theorem 3.2Suppose that(H′
1)~(H′3)are satis fied and β≤0 in(H′2),then for any λ∈(λ1,+∞),the boundary value problem(3.1)~(3.2)has at least a positive solution.
ExampleConsider the following fourth-order boundary value problem

[1]AGARWAL R P,Chow Y M.Iterative method for fourth order boundary value problem[J].J Comput App Math,1984,10:203-217.
[2]GUPTA C P.Existence and uniqueness results for the bending of an elastic beam equation[J].Appl Anal, 1988,26:289-304.
[3]DALMASSO R.Uniqueness of positive solutions for some nonlinear four-order operators[J].J Math Anal Appl,1996,201:152-168.
[4]GRAEF R,YANG B.Positive solutions of a nonlinear fourth order boundary value problem[J].Commun Appl Nonl Anal,2007,14:61-73.
[5]KORMAN P.Uniqueness and exact multiplicity of solutions for a class of fourth-order semilinear problems[J]. Proc Roy Soc Edinburg Sect A,2004,134:179-190.
[6]YAO Qing-liu.Positive solutions for eigenvalue problems of four-order elastic beam equations[J].Appl Math Lett,2004,17:237-243.
[7]CUI Yu-jun,ZOU Yu-mei.Existence and uniqueness theorems for fourth-order singular boundary value problems[J].Comput Math Appl,2009,58:1449-1456.
[8]ZHANG Yu-chuan,ZHOU Zong-fu.Positive solutions for fourth-order delay differential equation of boundary value problem with p-Laplacian[J].Chin Quart J of Math,2014,29:171-179.
[9]MA Ru-yun,XU Jia.Bifurcation from interval and positive solutions of a nonlinear fourth-order boundary value problem[J].Nonlinear Anal,2010,72:113-122.
[10]YAO Qing-liu.Existence of n solutions and/or positive solutions to a semipositive elastic beam equation[J]. Nonlinear Anal,2007,66:138-150.
[11]LU Hai-xia,Sun Li,Sun Jing-xian.Existence of positive solutions to a non-positive elastic beam equation with both ends fixed[J].Boundary Value Problems,2012,56:1-10.
[12]GUO Da-jun,SUN Jing-xian.Nonlinear Integral Equations[M].Jinan:Shandong Science and Technology Press,1987.
[13]KRASNOSEL’SKII M A.Topological Methods in the Theory of Nonlinear Integral Equations[M].Oxford: Pergamon Press,1964.
[14]SUN Jing-xian,LI Hong-yu.Global structure of positive solutions of singular nonlinear Sturm-Liouville problems[J].Acta Mathematica Scientia,2008,28A:424-433.
[15]MA Ru-yun.Nodal solutions of boundary value problems of fourth-order ordinary differential equations[J]. J Math Anal Appl,2006,319:424-434.
[16]RABINOWITZ P H.Some global results for nonlinear eigenvalue problems[J].J Functional Anal,1971,7: 487-513.
[17]SUN Jing-xian.The existence of positive solutions for nonlinear Hammerstein integral equations and their applications[J].Ann Math Ser,1988,9A:90-96.
tion:34B16,34B18
:A
1002–0462(2017)01–0007–09
date:2016-05-13
Supported by the National Natural Science Foundation of China(11501260);Supported by the National Natural Science Foundation of Suqian City(Z201444)
Biography:LU Hai-xia(1976-),female,native of Jianhu,Jiangsu,an associate professor of Suqian College, M.S.D.,engages in nonlinear functional analysis.
CLC number:O175.8
杂志排行
Chinese Quarterly Journal of Mathematics的其它文章
- A Generalized Schwarz Lemma
- Mean Values of the Hardy Sum
- The Generalization on Inequalities of Hermite-Hadamard’s Integration
- Lvy-Prohorov Metric on the Measure Space
- Existence and Uniqueness of Solutions to Singular Higher Order Two-point BVPs on Time Scales
- The Translational Hull of Strongly Inverse Wrpp Semigroups
