开关电感Boost变换器的失效机理及基于参数扰动的混沌控制方案研究

2017-06-05陈艳峰丘东元

电源学报 2017年3期

关键词：状态变量电感扰动

李姿，陈艳峰，张波，丘东元，陈曦

（华南理工大学电力学院，广州 510641）

开关电感Boost变换器的失效机理及基于参数扰动的混沌控制方案研究

李姿，陈艳峰，张波，丘东元，陈曦

（华南理工大学电力学院，广州 510641）

开关电感Boost变换器是新能源系统中应用较为广泛的一种高增益DC-DC变换器。由于变换器本身的特性，当电路参数的变化超出一定范围时，会发生分岔、混沌等非线性现象，造成变换器失效，此时变换器无法正常稳定运行并且工作性能下降，因此有必要控制变换器从混沌态重回稳定态。基于参数扰动混沌控制法的基本原理，设计了适用于峰值电流控制型开关电感Boost变换器的混沌控制方案。该方案可使工作于混沌状态的变换器能迅速返回周期-1态稳定工作，其输出电压增益得以提高、输出纹波显著降低，并且在输入和负载有较大扰动时变换器系统均能稳定工作。利用非线性理论对变换器失效机理进行分析和混沌控制，对于DC-DC变换器参数设计、稳定性分析和性能提升具有一定的实际应用价值。

开关电感Boost变换器；失效分析；混沌控制；参数扰动；周期-1轨道

太阳能光伏电池、燃料电池等新能源的输出电压往往比较低。为将低输出电压提高到并网逆变器直流线电压等级，首先考虑采用高增益DC-DC变换器升压。因此，提高DC-DC变换器增益是新能源并网发电系统函待解决的关键问题之一［1-2］。在目前所提出的众多高增益变换器拓扑中，开关电感Boost变换器具有结构相对简单，电感体积较小且工作模态对称、易于集成于一个磁芯之上等优点，因而得到广泛应用［3］。随着DC-DC变换器技术的不断提高，对于其质量和可靠性的诉求也越来越高。变换器的失效测试和分析，明确其失效原因，对于变换器设计改进、控制效果提升和避免变换器失效重复的发生有着关键作用。由于开关变换器本身的非线性特性，当电路参数的变化超出一定范围时，变换器会展现出现倍周期分岔、边界碰撞、混沌等复杂非线性动力学行为［4］。这些非线性行为是导致变换器失效的重要原因，也将造成变换器不能稳定运行、性能变差，系统运行状态无法预测和控制等［5-7］。因此，有必要利用某种非线性控制方法使得混沌运行的DC-DC变换器重回稳定工作态，以扩大变换器稳定工作的参数空间，并改善其工作性能，如提高其电压增益、降低输出纹波等。

1990年，美国 Maryland大学 Ott、Grebogi和Yorke等提出控制混沌的参数微扰方法（OGY法）［8］。自此，非线性系统的混沌控制研究蓬勃发展，各种混沌控制方法被相继提出［9-12］。其中一类是有待控目标轨道的混沌控制方法，如OGY法及其改进算法［13-14］、延迟反馈法、脉冲电压微分反馈控制法以及各种基于滤波器的反馈控制方法等。这类控制方法的优点在于理论严谨，在不改变系统的结构并保留其系统原有动力学特性的同时，将系统从混沌状态控制任意选定的目标轨道，具有良好的轨迹跟踪能力和稳定性；但其缺点是需要有一个目标函数或给定轨迹，工程实现比较困难［15-17］。另外一类是无待控目标轨道混沌控制方法，如零极点配置法、参数共振法等，其思想是通过控制使系统的Lyapunov指数下降为负，从而消除混沌。这类方法工程实现简单，但被控系统最终稳定到一条新的周期轨道，相应的控制器输出始终为非零量，且不能保证控制过程的稳定性。另外，普遍采用的斜坡补偿技术，从广义上讲也可以看作是一种无目标轨道混沌控制策略。虽然斜坡补偿方法可以有效拓宽变换器稳定工作的参数范围，但是斜坡信号的引入改变了原系统的动力学行为，使系统的动态响应性能下降，且过度补偿会增加状态变量波形的畸变程度，对变换器的功率因数产生负面影响［18］。文献［19］提出了一种适用于离散混沌系统的新型参数扰动混沌控制方法，并在二维Henon系统得以验证。该方法选取混沌吸引子中不稳定周期-1轨道UPO-1（unstable period-1 orbit）为控制目标，通过叠加控制变量的扰动值，达到混沌控制的效果。与现有的控制方法相比，该方法摆脱了对不动点类型的限制，适用于所有类型的不动点的控制。

本文将文献［19］提出的参数扰动混沌控制方法应用于开关电感Boost变换器，设计了适用于该变换器的混沌控制方案，并进行了数值和模型仿真，研究了变换器增益、输出纹波等性能的提升，分析了变换器的稳定性。利用混沌控制方法对实现DC-DC变换器高增益有着重要意义和应用价值。

1 PCMC开关电感Boost变换器的工作原理与特性简析

1.1 开关电感Boost变换器工作原理

峰值电流控制模式PCMC（peak current mode control）开关电感Boost变换器的电路原理如图1所示，图中虚线内电路为“开关电感”，由2个大小相等的电感 L1、L2及 3个二极管 D1、D2、D12构成。

图1 PCMC开关电感Boost变换器原理Fig.1 Basic diagram of PCMC switched-inductor Boost converter

假设变换器工作在电感电流连续导通模式CCM（continuous-conduction mode）下，根据开关管VT和二极管D导通情况，变换器在一个周期内存在2个不同的工作状态，如图2所示。

当时钟信号来临时，开关管VT导通，二极管D1、D2导通，D12截止，电感 L1、L2并联充电；当电感电流iL1（iL2）上升至Iref时，VT关断，二极管D1、D2截止，D12导通，电感 L1、L2与电源E串联对负载提供电能，电感电流iL1（iL2）下降。直至下一周期到来，开关管VT再次导通。电感电流iL1与时钟周期信号Clock工作波形如图3所示。

图2 开关电感Boost变换器工作状态Fig.2 Working modes of the Boost converter

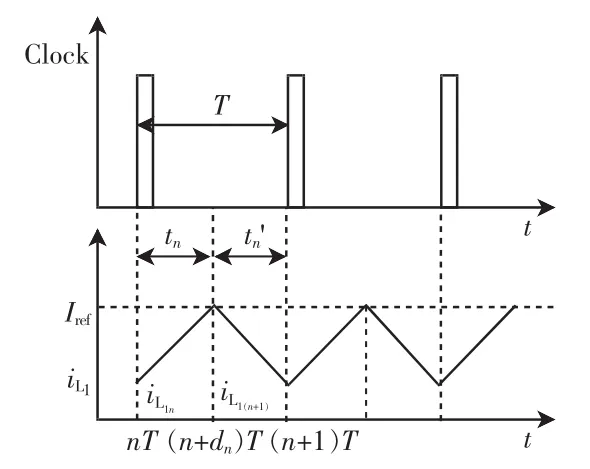
图3 电感电流iL1与时钟周期信号Clock波形Fig.3 Waveforms of iL1and Clock signals

当电路处于稳态时，根据电感L1两端伏秒平衡原理，其输出电压增益为

式中：UC为电容电压（负载电压）达到稳态时的平均值；D为稳态时VT的占空比。

1.2 频闪映射建模

开关电感Boost变换器中存在2个储能电感及1个电容，但由于2个电感工作状态相同，所以本质上看，该变换器仍属于二阶电路。需要注意的是，iL1和iL2分别连续，但在变换器工作于图2（a）的状态时，干路总电流即电源电流等于2倍的iL1，变换器工作于图2（b）的状态时，电源电流等于1倍的电感电流iL1，所以电源电流并不连续。为了方便计算及采样，取iL1和电容电压uC为状态变量。根据iL1和电源电流的数量关系，可以得到电源电流变化情况。在CCM下，可分别列写出2个相应电路的状态方程，即

式中：x=［iL1,uC］T；n为整数；dn为第 n个周期的占空比；E为输入电压；T为时钟周期；Ai和Bi（i=1,2）为系数矩阵，分别表示为

求解式（2），可得到第n+1个开关周期开始时刻的状态变量xn+1和第n个开关周期开始时刻的状态变量xn的频闪映射，即

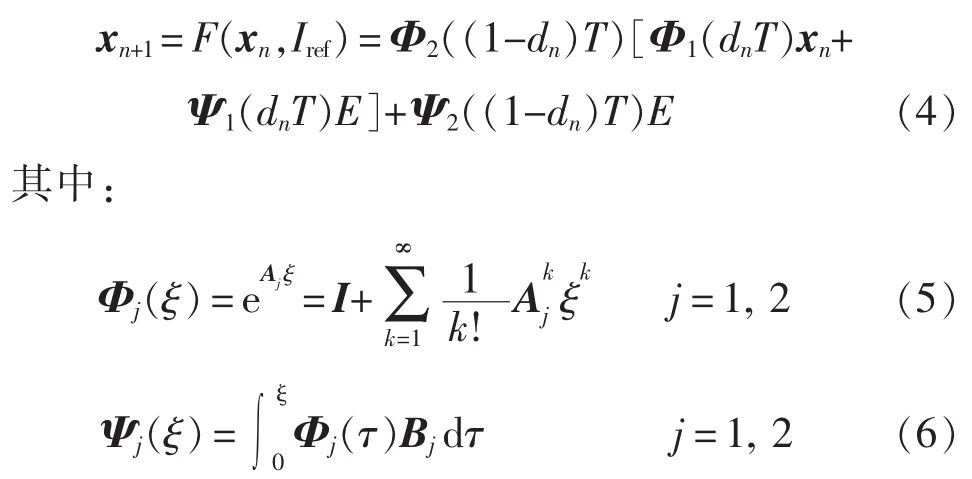
式中，ξ为式（4）中的dnT。定义异步切换函数为

当s（xn,dn）=0时，开关管VT由导通状态变为关断状态，利用数值方法求解此非线性方程，即可求出式（4）中所需的dn。

1.3 非线性动力学行为简析

电路参数设置如下：T=100 μs（f=10 kHz），L=L1= L2=0.5 mH，R=10 Ω，C=50 μF，E=10 V，Iref=0～15 A。根据频闪映射模型式（4）及异步切换函数式（7），可得到电感电流iL1和电容电压uC随参考电流Iref变化的分岔波形，如图4所示。

在参考电流Iref由0 A增加到15 A的过程中，变换器首先在Iref=5.7 A时出现倍周期分岔，由稳定的周期-1态变为周期-2态，此时占空比d=0.47，电压增益G=2.77。此后，随着参考电流的增大，系统经过多次倍周期分岔后最终进入了混沌状态。从图中可以看到，系统处于混沌状态时，单一的Iref往往对应多个周期轨道。本文的目标即是在这些轨道中，选取所需UPO-1并使之固定下来，使处于混沌状态的变换器重新回归周期-1态工作，并使变换器输出电压增益、纹波等性能指标得以改善。

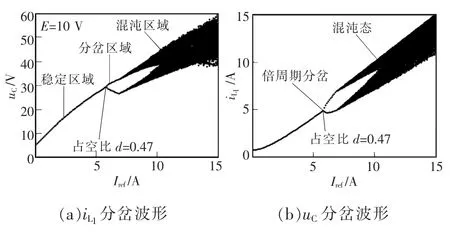
图4 以Iref为分岔参数时分岔波形Fig.4 Bifurcation diagrams of the state variables with Irefas bifurcation parameter

2 基于参数扰动法的混沌控制方案及其应用

2.1 不稳定周期轨道的参数扰动法简介

不稳定周期轨道的参数扰动法是由Alexander Jimenez-Triana、陈关荣等［19］于2015年提出的一种适用于离散系统的新型混沌控制方法，可以在混沌系统的诸多不稳定周期轨道中选取并固定所需要的周期-1轨道。在每周期开始时对状态变量进行采集，通过数值计算得到控制变量的扰动量，并将此扰动量叠加到原控制变量上得到本周期新的控制变量。对于n维系统，需要对控制变量进行n步扰动以实现混沌控制。考虑具体的二维离散系统，在第n+1和n个周期的状态变量离散映射描述为

式中：xn∈R2；F（·）为光滑矢量函数；pn为每个周期的控制变量，对应于开关电感Boost变换器，pn为每周期内参考电流。

假设系统在pn=P时处于混沌状态，定义不动点Xp=F（Xp，P），则在目标轨道（Xp，P）的邻域内，系统可线性近似表示为

式中：M为系数矩阵；N为参数矩阵。二者分别表示为

由式（9）可得

当系统满足周期-1稳态时，有xn+2=xn+1=Xp，从而可得到二维系统的两步扰动值为

即每个周期控制参数需要调整为

2.2 控制参数计算

将不稳定周期轨道的参数扰动控制法应用到处于混沌状态的开关电感Boost变换器中。首先应该确定二维状态变量x及使系统处于混沌状态的控制变量Xp。根据离散建模，x=［iL1,uC］T，参考电流被选作为状态变量及控制参数，从图4可知，当参考电流Iref＞10 A时，系统处于混沌状态，可在该范围内选取Iref=12 A。

令式（4）中xn=xn+1，可以求出混沌状态下的不动点为

由式（4）、式（10）可计算得到参数矩阵和系数矩阵分别为

由式（15）可求得加入参数扰动混沌控制方法后第n和（n+1）周期的参考电流，即

2.3 仿真验证

根据前文介绍的混沌控制方法原理和相关参数计算，设计了适用于开关变换器的混沌控制方案，并利用PSIM电路仿真软件搭建了如图5所示的仿真模型。其中，控制电路是在传统峰值电流控制模式基础上增加了一个扰动量计算单元。计算单元的工作开始时间由step模块决定，其工作原理是在每周期开始时采集状态变量，根据式（18）计算得到本周期的参考电流。根据图5仿真模型，可以得到状态变量iL1和uC的时域波形如图6所示。

由图6可见，0～0.010 0 s时，参考电流Iref为12 A，电路工作在混沌状态；0.010 0 s时，step模块跳变，扰动量计算单元工作，参考电流在每个开关周期都被重新整定，系统从混沌状态被控制到周期-1态。

电感电流功率频谱以及状态变量相轨迹，分别如图7和图8所示。从图7可以看出，通过参数扰动法，功率频谱由连续的混沌态变为离散的周期态，即处于混沌状态的开关电感Boost变换器可以重新工作在UPO-1轨道中。由图8可以看出，被控UPO-1轨道存在于原混沌吸引子中，在控制过程中并没有产生新的周期轨道。被控周期-1态的占空比d=0.62，电感电流和电容电压在每时钟周期末被控制到平衡点（10.753 9 A,45.615 1 V）上，此时输出电压平均值为43 V，电压增益G=4.3，相较于图4中iL1第1次分岔时的d=0.47和G=2.77有了较明显的提升。电流纹波峰峰值从混沌状态的3.2 A控制到周期-1轨道的1.3 A，电压纹波峰峰值从混沌状态下的14.5 V控制到周期-1轨道的5 V，纹波明显下降。由此可见，通过混沌控制，变换器输出电压增益及纹波特性得到了明显改善。

图5 PSIM仿真模型Fig.5 Simulation model in PSIM

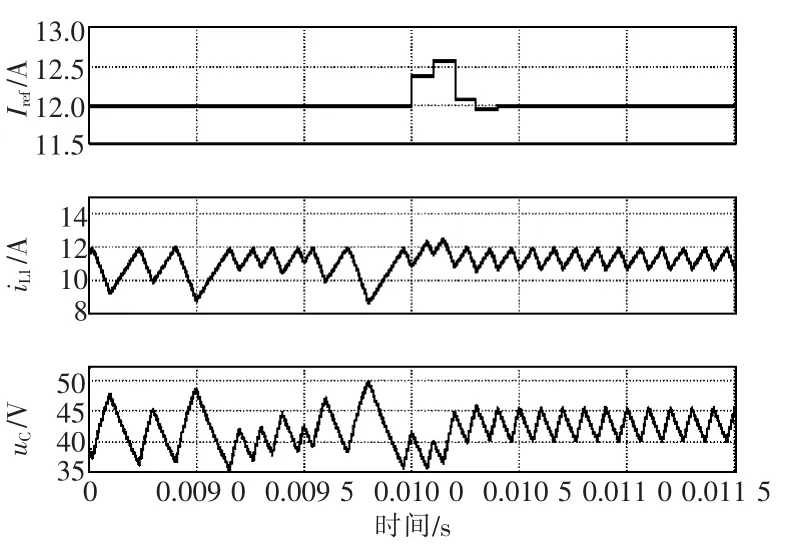
图6 状态变量仿真时域波形Fig.6 Simulated time-domain waveforms of state variables

图7 控制前后iL1频谱Fig.7 Power spectrum of iL1before and after control

图8 混沌吸引子和固定UPO-1相图Fig.8 Simulated phase portrait of chaotic attractor and fixed UPO-1

3 参数扰动时系统的稳定性分析

开关变换器系统在实际工作中，其输入电压和负载通常容易发生扰动，导致变换器系统的工作状态及稳定性可能发生变化。

3.1 控制系统的雅克比矩阵

本文使用图1所示控制模式PCMC下的频闪映射模型。由于参考电流Iref经过了参数扰动调整，因此异步切换函数式（7）变为

当s（xn，dn）=0时，开关管VT由导通状态变为关断状态，利用数值方法求解此非线性方程，即可求出式（4）所需的dn。

开关电感Boost变换器在不动点Xp邻域的雅克比矩阵定义为

由式（4）和式（19）可得

将式（21）～式（24）代入式（20），由矩阵特征方程

求得二阶雅克比矩阵J（Xp）在不同控制参数条件下特征根λ1和λ2。由根据文献［16］的分析知：当λ1和λ2其中一个特征值等于1，另一个模小于1（在复平面单位圆内）时，系统在该平衡点处发生鞍结分岔（折叠分岔）；当λ1和λ2其中一个等于-1，另一个模小于1时，系统在该平衡点处发生叉形分岔（倍周期分岔）；当λ1和λ2为一对共轭复数且模为1时，系统在该平衡点处发生环面分岔。

3.2 负载扰动时系统稳定性分析

在图5的混沌控制系统下，保持其他参数不变，负载电阻R在1～50 Ω的范围内变化，根据频闪映射模型式（4）及异步切换函数式（19），可得iL1和uC的分岔波形，如图9所示。

根据式（25）可求得负载电阻R变化时系统特征值的运动轨迹，如图10所示，由图10可见，当R=16.59 Ω时，有一个特征根为-1，表明系统发生了倍周期分岔，这一结果与图9通过数值仿真所得到分岔点相一致。由图9知，当R在（1 Ω，16.59 Ω）的范围内时，iL1及uC均可稳定在周期-1轨道上，表明该控制方案对负载电阻扰动具有良好的抗干扰性。

图9 混沌控制系统分岔参数R的分岔波形Fig.9 Bifurcation waveforms of state variables with bifurcation parameter R in chaotic control system

图10 混沌控制系统随R变化特征值轨迹Fig.10 Eigenvalue traces of chaotic control system with the change of R

3.3 输入电压扰动时系统稳定性分析

在图5的混沌控制系统下，保持其他参数不变，输入电压E在1～20 V的范围内变化，根据频闪映射模型式（4）及异步切换函数式（19），可得iL1和uC的分岔波形，如图11所示。由图可见，当E＞3.78 V时，iL1及uC均可稳定在周期-1轨道上，表明该控制方案对输入电压扰动也具有良好的稳定性。

根据式（25）可求得输入电压E变化时系统特征值的运动轨迹，如图12所示。由图12可见：当输入电压E=3.78 V，系统的特征根为一对位于单位圆上的共轭复数，表明此时系统出现了环面分岔；随着E的增大，特征根处于单位圆内，系统一直处于周期-1态。这一结果与图11通过数值仿真所得到分岔点相一致。

图11 混沌控制系统分岔参数E的分岔波形Fig.11 Bifurcation waveforms of state variables with bifurcation parameter E in chaotic control system

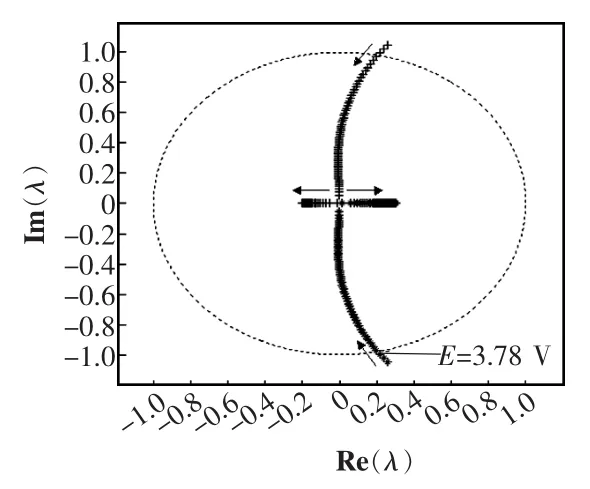
图12 混沌控制系统特征值随E变化轨迹Fig.12 Eigenvalue traces of chaotic control system with the change of E

4 结语

本文分析了开关电感Boost变换器中的非线性及混沌现象，明确了因非线性行为导致的变换器失效机理，并将参数扰动混沌控制方法应用于开关电感Boost变换器，设计了适用于开关电感Boost变换器的混沌控制方案。通过理论分析和数值仿真证实了该控制方案可以在高增益变换器的基础上进一步提高变换器电压增益，减小电感电流和输出电压纹波，证明了该控制方案在受到输入电压及负载干扰的情况下具有良好的稳定性，在DC-DC变换器控制和工程应用方面具有一定的指导意义。

［1］Li Wuhua,He Xiangning.Review of nonisolated high-step-up DC/DC converters in photovoltaic grid-connected applications［J］.IEEE Transactions on Industrial Electronics,2011, 58（4）：1239-1250.

［2］韩晓明,马皓,陈隆宇.能馈电子负载中低压大电流输入高增益变换器设计［J］.电源学报,2011,9（4）：46-51. Han Xiaoming,Ma Hao,Chen Longyu.Design of high-gain converter for low input voltage and high input current in energy feedback electronic load system［J］.Journal of Power Supply,2011,9（4）：46-51（in Chinese）.

［3］王挺,汤雨.基于开关电感的有源网络升压变换器的研究［J］.电工技术学报,2014,29（12）：73-79. Wang Ting,Tang Yu.Study of active network DC-DC boost converter based on switched-inductor［J］,Transactions of China Electrotechnical Society,2014,29（12）：73-79（in Chinese）.

［4］刘洪臣,杨爽,王国立,等.基于开关电感结构的混合升压变换器非线性现象研究［J］.物理学报,2013,62（15）：58-65. Liu Hongchen,Yang Shuang,Wang Guoli,et al.Nonlinear phenomena in the hybrid step-up converter with switchedinductor structure［J］.Acta Physica Sinica,2013,62（15）：58-65（in Chinese）.

［5］Tse C K.Complex behavior of switching power converters［M］.1st Edition.Boca Raton,USA：CRC Press LLC, 2004.

［6］Cheng K W E,Liu M,Wu J.Chaos study and parameterspace analysis of the DC-DC buck-boost converter［J］.IEEE Proceedings of Electric Power Applications,2003,150（2）：126-138.

［7］张波,李萍,齐群.DC-DC变换器分叉和混沌现象的建模和分析方法［J］.中国电机工程学报,2002,22（11）：81-86. Zhang Bo,Li Ping,Qi Qun.Methods for analyzing and modeling bifurcations and chaos in DC-DC converter［J］. Proceedings of the CSEE,2002,22（11）：81-86（in Chinese）.

［8］Ott E,Grebogi C,Yorke J A.Controlling chaos［J］.Physical Review Letters,1990,64（11）：1196-1199.

［9］卢伟国,周雒维,罗全明,等.BOOST变换器延迟反馈混沌控制及其优化［J］.物理学报,2007,56（11）：6275-6281. Lu Weiguo,Zhou Luowei,Luo Quanming,et al.Time-delayed feedback control of chaos in BOOST converter and its optimization［J］.Acta Physica Sinica,2007,56（11）：6275-6281（in Chinese）.

［10］周宇飞,陈军宁,谢智刚,等.参数共振微扰法在Boost变换器混沌控制中的实现及其优化［J］.物理学报,2004,53（11）：3676-3683.Zhou YuFei,Chen JunNing,Tse C K,et al.Application of resonant parametric perturbation to the chaos control in Boost converter and its optimization［J］.Acta Physica Sinica,2004,53（11）：3676-3683（in Chinese）.

［11］王鹤,李耀峰,张守龙,等.基于自适应Terminal滑模的混沌振荡控制［J］.电力系统及其自动化学报,2013,25（3）：152-157. Wang He,Li Yaofeng,Zhang Shoulong,et al.Chaotic oscillation control based on adaptive terminal sliding mode［J］.Proceedings of the CSU-EPSA,2013,25（3）：152-157（in Chinese）.

［12］Lu Weiguo,Zhou Luowei,Luo Quanming,et al.Filter based non-invasive control of chaos in Buck converter［J］. Physics Letters A,2008,372（18）：3217-3222.

［13］Shinbrot T,Ott E,Grebogi C,et al.Using chaos to direct trajectories to targets［J］.Physical Review Letters,1991,65（26）：3215-3218.

［14］Chakrabarty K,Banerjee S.Control of chaos in piecewise linear systems with switching nonlinearity［J］.Physics Letters A,1995,200（2）：115-120.

［15］Ushio T.Limitation of delayed feedback control in non-linear discrete-time systems［J］.IEEE Trans.on CAS-I,1996,43（9）：815-816.

［16］彭召旺,钟廷修,冯正进.高周期混沌轨道的最优反馈控制［J］.控制与决策,2001,16（3）：326-328,340. Peng Shaowang,Zhong Tingxiu,Feng Zhengjin.Optimal feedback control for higher-period chaotic orbits［J］.Control and Decision,2001,16（3）：326-328,340（in Chinese）.

［17］罗晓曙.DC-DC变换器的非线性动力学行为与混沌控制［M］.北京：科学出版社,2012.

［18］杨平,包伯成，沙金，等.开关变换器斜坡补偿动力学机理研究［J］.物理学报,2013,62（1）：49-57. Yang Ping,Bao Bocheng Sha Jin,et al.Dynamical mechanism of ramp compensation for switching converter［J］. Acta Physica Sinica,2013,62（1）：49-57（in Chinese）.

［19］Jimenez-Trianna A,Chen Guanrong,Gauthier A.A parameter-perturbation method for chaos control to stabilizing UPOs［J］.IEEE Trans on Circuits and Systems-II,2015,62（4）：407-411.

Study on Failure Mechanism of Switched-inductor Boost Converter and Chaos Control Scheme Based on Parameter-perturbation

LI Zi,CHEN Yanfeng,ZHANG Bo,QIU Dongyuan,CHEN Xi
（School of Electric Power,South China University of Technology,Guangzhou 510641,China）

Switched-inductor Boost converter has been widely used in the new energy systems.Whereas its complex nonlinear dynamic behaviors,such as bifurcation and chaos,have led to the failure of converter.Therefore,it is necessary to control the converter to stable state from chaotic state.In this paper,a new chaotic control scheme based on parameter-perturbation method is proposed and applied to a peak current-mode controlled switched-inductor Boost converter.And the converter operating in chaotic state can be controlled quickly to the period-1 orbit with better performances,such as higher voltage-gain and lower output ripples.In addition,the system can work stably when the input or load resistance has large disturbance,which means that the new scheme has better stability against input voltage or load resistance disturbance.The analysis of failure mechanism and chaos control based on the nonlinear characteristics of the converter can be helpful for the design of circuits’parameters and the performance improvement.

switched-inductor Boost converter;failure analysis;chaos control;parameter perturbation;period-1 orbit