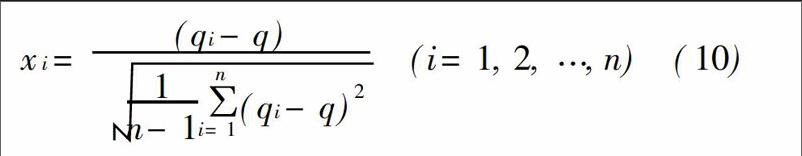年最大洪峰流量群居蜘蛛优化投影寻踪预测模型
2017-06-05王文川刘惠敏雷冠军刘宽邱林
王文川 刘惠敏 雷冠军 刘宽 邱林
摘要:年最大洪峰流量预测,受较多的复杂因素的影响,不确定性较强,用常规统计方法做出准确预报具有较大困难。从水文序列本身出发,提出将投影回归模型应用于年最大洪峰流量预测,为了更好获得投影寻踪模型参数和预测精度,提出了运用延迟相关系数法确定回归预测因子、群居蜘蛛算法优化投影寻踪模型最佳投影方向参数n、利用最小二乘法确定多项式的权系数c、岭函数个数M的群居蜘蛛优化投影寻踪年最大洪峰流量预测模型,结合长江宜昌站(1882年-2004年)的年最大洪峰流量资料进行实例预测,训练阶段平均绝对相对误差为8.61%,预测阶段平均绝对相对误差为10.5 1%,该模型预测效果较好,模型结果稳定,可有效应用于年最大洪峰流量预测。
关键词:SSO算法;参数投影寻踪;混合智能;年最大洪峰流量;预测
中图分类号:TV 124 文献标识码:A 文章编号:1672-1683(2017)02-0009-06
鉴于年最大洪峰流量在防洪渡汛工作中具有重要作用,所以其预测是中长期水文预报的重点。但由于其涉及较大的时空尺度范围,并受到大气运。王渺林在趋势分析与周期分析的基础上对年最大洪峰流量的演变规律进行研究。金鑫家运用小波分析对水文序列进行由粗到细的分析,分析了年最大洪峰流量的周期和预报:王文圣等人在小波变换序列的基础上提出了最近邻抽样回归组合预报,结果表明提出的方法好于谐波预报法:宋荷花等利用模糊模式识别模型对湘江湘潭站年最大洪峰流量进行预报:李红霞等探讨了基于贝叶斯正则化方法的神经网络年最大洪峰流量预测模型:孙树青等将统计相关性分析与模糊方法相结合,建立了基于BP神经网络的最大洪峰流量进行预报模型,这些工作作为对最大洪峰流量预测建模的有益尝试,促进了其发展,但人工神经网络在解决预报问题方面仍存在网络结构选择困难、全局搜索能力差、易陷入局部最优值点且模拟结果不稳定等问题,在一定程度上限制了其在实际生产中的推广应用。赵璀将灰色系统理论运用到中长期水文预报中,取得了较好的结果。张汉雄认为年最大洪峰流量序列是一个纯随机现象,因而选择采用马尔科夫链给出预测值的大致范围,但该方法的结果受序列长度的影响较明显。胡致强在自适应控制理论发展的基础上,运用Kalman滤波对年最大洪峰流量进行预报,如果模型和水文系统不匹配,則会使预报误差较大。
投影寻踪将应用数学、现代统计与计算机技术相结合进行数据处理,在解决样本数量少和维数较大等问题时,具有明显的优势,在评估、聚类分析、洪水预报等领域得到了很好的应用。
投影寻踪建模过程是利用线性投影的多个多元回归的线性组合,优选投影方向a、多项式系数c和岭函数个数M的最优组合。根据niedman和Stu-etzle提出的投影寻踪技术多重平滑实现法,核心是采用多层分组迭代交替优化方法,选取m组参数以及岭函数的最优项数目。把参数分为若干组,选择其中一组作为参数寻优的对象,其他组都给定一初值。求得结果后,把寻优所得的参数极值点作初值,另选一组参数在这一初值下寻优,多次反复寻优直到最后的一组参数使得目标函数达到最小。
传统的投影寻踪方法寻优速度较慢,且寻优结果与初始值的设定有关。为了更好地寻找模型的参数,文献分别采用不同的寻优算法与投影寻踪算法相结合,确定最优的参数组合,以此来进行预测。本文提出了通过延迟相关系数法确定回归预测因子、群居蜘蛛算法f Social Spider Optimization,SSO)优化投影寻踪(Projeetion pursuit regres-sion,PPR)模型最佳投影方向参数a,最小二乘法确定多项式权系数c,合格率控制参数M个数相结合的混合智能投影寻踪年最大洪峰流量预测模型,结合长江宜昌站(1882年-2004年)的年最大洪峰流量资料进行了实例分析。
1基于参数投影寻踪回归的年最大洪峰流量建模原理
投影寻踪回归法是Friedman和Stuetzle思想是寻找能反映高维数据的结构特征的若干个投影方向,将高维数据投影到一维空间,通过优选出的岭函数的代数和去逼近回归函数,以此构造模型。其回归预测建模的原理主要如下。
设x为p维的预测因子,a为p维投影向量,f(x)为预测的年最大洪峰流量,为了解决多元线性回归不能有效反映实际非线性的问题,投影寻踪回归模型用一系列的岭函数g(aTx)的代数和去逼近回归函数f(x),因此,预测量与预测因子的投影回归关系能被表达为
(1)式中:M为岭函数的个数;g为岭函数。当M,g等于1时,式(l)就变为常规的多元函数。
在Friedman和Stuetzle最初的研究中提出的采用庞大的简单函数集合,通过分层组迭代交替优化技术去光滑逼近,实现难度较大,在很大程度上限制了该模型的推广与应用。Hwang等人研究表明Hermite多项式具有较强的光滑、趋势、动态、非线性拟合能力,且多项式次数的增加会增强起拟合复杂程度的能力,因此,可采用可变阶递推的正交Hermite多项式拟合一维岭函数。则投影回归关系式就变为
(2)式中:n表示输入样本的个数;zi表示第i个输入样本在投影方向。上的投影,其表示达式为
(3)
j为多项式的阶数;c为多项式的系数;h为正交Hermite多项式,h的数学表达式如下:
(4)式中;j!代表多项式阶数i的阶乘;φ(z)=
(5)
由此回归预测建模就可转化为求解式(6)的最小化问题。
(6)
(7)
(8)
根据水文情报预报规范(GB/T 22482-2008),合格预报次数与预报总次数之比的百分数为合格率QR,其计算公式为:
(9)式中QR为合格率(%);nh为合格预报的次数:n为预报的总次数。
所以,投影寻踪回归预测的关键就转化为优选投影回归模型的投影方向参数a、多项式权系数c和岭函数的个数M,参数优选的结果直接影响模型的泛化能力、模拟及预测精度。
2群居蜘蛛优化算法
群居蜘蛛優化算法(SSO)是由Cuevas等人基于对群居蜘蛛的协作行为,提出的一种新的随机全局优化技术。群居型蜘蛛是群居性昆虫的典型例子,是群体成员能够完成一系列复杂的协同行为的蜘蛛。在群居蜘蛛群落中,每一个个体,由于性别的差异,完成一系列任务如:捕食、交配、织网和相互交流的任务。蜘蛛的网是群落重要的一部分,它不仅是全体成员生存环境的一部分,而且是它们之间的交流渠道。因此重要的信息(例如捕食或者是交配)由网通过震动的形式传播。这些信息,被当作局部的知识,每个成员利用这些知识来指导它们各自的协作行为,同时影响了群落的社会规范。
群居蜘蛛生物群落有两个基本的组成部分:群落成员和公共的网。群落成员被分为两类:雌蜘蛛、雄蜘蛛。群居蜘蛛是高度的母系氏种群。一些研究表明雄蜘蛛的数量差不多达到全部群落成员数目的30%。群落成员之间有直接和间接的交流。直接的交流意味着身体接触或者是体液的交换诸如交配。对于间接的交流,公共的网作为一个交流媒介用来传达重要的信息,这些信息每一个群落成员都能够感受得到。这些被编码成震动的信息是成员之间集体协作的一个关键的方面。群落成员将震动解码成几条信息诸如被捕获的动物的大小,邻居成员的特征等等。这种震动的强度依赖于激发他们的蜘蛛的重量和距离。
它们相互作用的方式是依赖于蜘蛛的性别的。雌蜘蛛展示了群居式的主要倾向,由于震动依赖于激发他们的蜘蛛的重量和距离,很强有力的震动或者是大蜘蛛激发的,或者是距离较近的蜘蛛发出的。与雌蜘蛛不同的是,雄蜘蛛的行为是生殖导向的。雄性蜘蛛将他们自己视为雄性组织的领袖,他们控制着群落的资源。因此,雄性个体被分为两类:优势者和劣势者。优势的雄性蜘蛛和劣势的雄性蜘蛛比起来有更好的适应度。在一个典型的行为中,优势蜘蛛被公共网上的最近的雌性蜘蛛所吸引。相反,劣势雄性蜘蛛围绕在优势雄性群体的周围利用优势雄性种群浪费的资源。
交配是一个重要的生理行为,该行为不仅保证了种群的延续,而且能够使信息在种群之间交流。群居蜘蛛的交配发生在优势雄性蜘蛛和雌性蜘蛛之间。在这种情况下,当一个优势蜘蛛在一只或是更多的雌性蜘蛛的特定的范围内,它们和所有的蜘蛛交配为了产生后代。
作为优化技术其求解优化问题最小值的步骤可参考文献,在此不再赘述。
3年最大洪峰流量混合智能预测建模步骤
根据前面介绍投影寻踪回归建模的原理和群居蜘蛛优化算法求解最小值优化问题的步骤,年最大洪峰流量混合智能预测建模的具体步骤如下。
(1)数据归一化。为消除数据在量纲和标准差数值水平上的差异,利用下式对数据进行标准化处理:
(10)式中:qi表示年最大洪峰流量序列;xi表示归一化后的流量序列;n表示序列的容量。
(2)确定预测因子。利用相关技术确定径流序列的预测因子。时序xi延迟k步的自相关系数Rk可通过下式获得:
(11)
(12)
(13)则推断时序xi延迟k步相依性显著,将xi-k作为xi的预测因子。μα12从正态分布表中查得,在本文研究中取80%的置信水平。
(3)生成初始投影方向。设定蜘蛛的种群规模Ⅳ,按约束条件式(7)生成N组PP模型投影方向a的初始值。
(4)计算多项式权系数c。根据生成的投影方向,利用式(3)计算投影值z,利用式(4)计算r阶Hermite多项式hr(z),然后最小二乘法计算多项式权系数c。
(5)计算相应的适应度值,评价蜘蛛个体。根据第4步得到权系数c,利用式(2)计算回归值,利用式(6)计算适应度值,进入群居蜘蛛优化算法的步骤2。经过群居蜘蛛优化算法一系列的机制,更新个体,进行迭代计算,获得最优的投影方向参数。和多项式权系数c,第一个岭函数优化结束。
(6)模型优化终止和结果输出。根据优选得到的投影方向参数a和多项式权系数c,计算拟合残差和合格率,如果满足合格率终止准则,输出预测值和相应的参数,用εi代替yi,转入(3)进行下一个岭函数的优化。为了避免程序进入死循环,模型优化终止准则采用合格率和最大岭函数个数相结合的方式。
4实例验证
选取长江宜昌站1882年-2004年共123年的年最大洪峰流量序列{q1|i=1,2.…,123},应用前113年(1882年-1994年)训练投影寻踪混合智能预测模型确定模型参数,用后10年(1995年-2004年)的年最大洪峰流量进行检验。通过计算计算该序列前30阶自相关系数Rk和与之相应的上、下限R1k,R2k值,其中置信水平取80%,计算结果表明R1,R2,R3,R20,R21,R22,R25,R28,R30的相依性在置信水平80%的条件下是显著的。所以,对qi预测的因子取为qi-1,qi-2,qi-3,qi-20,qi-21,qi-22,qq-25,qqi-28,qqi-30,则前113年(1882年-1994年)可得到83组训练数据。训练过程,a的取值范围为[-l,1],Hermite多项式阶数为r=6,群居蜘蛛优化算法的种群规模N=50,最大迭代次数Gmax为500;岭函数的最大个数Mmax=3。经群居蜘蛛算法和最小二乘方法混合优化,得到长江宜昌站年最大洪峰流量的预测模型为
(14)
根据得到的混合智能投影寻踪年最大洪峰流量预测模型,计算1995年-2004年的年最大洪峰流量预测值。图1给出了本文提出模型的(1912年-1994年)训练模拟值和(1995年-2004年)预测值与宜昌站年最大洪峰流量观测值的对比图。训练阶段和预测阶段相关误差统计分析结果见表1。根据水文情报预报规范(GB/T 22482-2008),合格率超过85%的为预报等级为甲等。根据表1中统计分析结果可以看出,在训练阶段的合格率为94.0%,在检验阶段的合格率为90%,预报等级为甲等。同时也可以看出,在训练阶段相对误差绝对值在[0,15]区间内的百分比达84 30%,在[0,10]区间内的百分比达67.5%:在检验阶段相对误差绝对值在[0,15]区间内的百分比达70.0%,在[0,10]区间内的百分比达60%:训练阶段的平均绝对相对误差仅有8.61;检验阶段的最大相对误差绝对值为22.44%,最小相对误差绝对值为1.76%,平均绝对相对误差仅有10.51。所以提出混合智能投影寻踪年最大洪峰流量预测模型宜昌站的年最大洪峰流量的模拟预测获得了非常好的效果。
为了测试预报结果的稳定性,在相同的计算机系统和环境下,不改变种群规模和迭代次数条件下,运行10次,优选出的模型参数没有变化,说明提出的混合智能投影寻踪预测模型稳定性强。
5结论
对于年最大洪峰流量预测,传统的统计分析方法很难取得满意的效果,这从对其预测的文献检索也可以印证,其研究成果明显少于其他中长期水文预报(如年、月径流量)的预报。为此,本文尝试性地将参数投影寻踪模型引入年最大洪峰流量预报,提出了运用延迟相关系数法确定回归预测因子、群居蜘蛛算法优化投影寻踪模型参数的混合智能投影寻踪年最大洪峰流量预测模型。以长江宜昌站(1882年-2004年)的年最大洪峰流量资料为依据进行了实例分析,结果表明,建立模型能获得很好的精度,检验阶段预报合格率达到90%,明显高于文献中用谐波预报法所得的检验阶段合格率68.2%以及基于小波变换序列的最近邻抽样回归组合预报所得的检验阶段合格率81.8%。同时提出模型智能化程度高,预测因子,模型参数可以完全有计算机完成,且结果稳定性好,可有效应用于年最大洪峰流量预测,值得在实际中推广应用。