巧构平行四边形

鞠红军

巧构平行四边形

鞠红军

同学们都知道，两组对边分别平行的四边形是平行四边形.那么如何借助有限的条件来构造平行四边形呢？下面，我们一起来研究.

类型1：已知一个固定的顶点

【解析】只根据一个点，无法确定平行四边形的边的长度和方向，更无法确定另外三个顶点的位置，所以无法构造出平行四边形.

类型2：已知两个固定的顶点

例1在平面直角坐标系中，已知点A（4，0）、B（-2，0），P、M是平面直角坐标系内任意两点，如果以A、B、P、M为顶点构造平行四边形，P、M两点在位置上有什么要求？

【解析】A（4，0）、B（-2，0）两点是确定的，P、M两点是不确定的.以AB为分类标准，分两种情况讨论：（1）如图1，当AB为平行四边形的一条边时，则要求线段PM平行且等于线段AB.（2）如图2，当AB是对角线时，则要求PM是平行四边形的另一条对角线.注意：在两种情况下，四边形APBM都是中心对称图形.

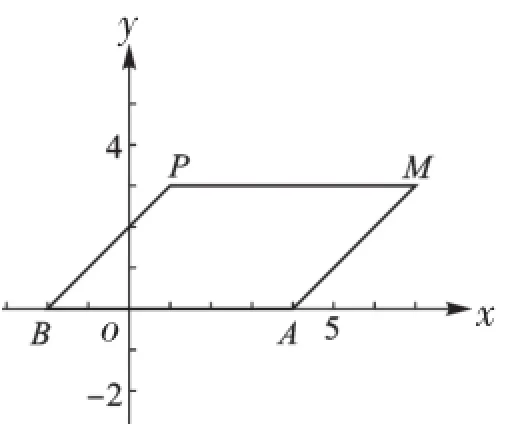
图1

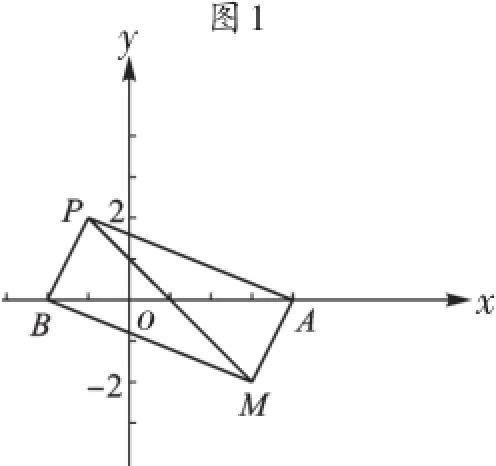
图2

如果给P、M两点再添上其他要求呢？

【变式】在平面直角坐标系中，已知点A（4，0）、B（-2，0），点P在y轴上，点M在一次函数y=-x+5的图像上，求P、M的坐标.

【解析】AB=6.若PM平行于AB，如图3，因为点P在y轴上，所以M点的横坐标有两种情况：6或-6.当M点的横坐标为6时，代入一次函数解析式中，可求出M的坐标为（6，2），当M点的横坐标为-6时，代入一次函数解析式中，可求出M的坐标为（-6，8）.则相应的P点坐标为（0，2）或（0，8）.

【解析】A、B、C这三点是确定的，过△ABC的三个顶点分别画对边的平行线，三条直线两两相交，便可产生3个符合条件的点：D1、D2、D3（如图5）.

图3

图5

若PM是平行四边形APBM的对角线，如图4，设P的坐标为（0，p），利用平行四边形的对称中心（1，0），得M的坐标为（2，-p），代入直线y=-x+5中，求出p=-4.所以P的坐标为（0，-4），M的坐标为（2，4）.

图4

类型3：已知三个固定的顶点

例2在平面直角坐标系中，已知A（4，0）、B（-2，0）、C（0，2），如果以点D、A、B、C为顶点的四边形是平行四边形，求点D的坐标.

①AC为对角线时，由于将点B（-2，0）向右平移2个单位再向上平移2个单位可得到C（0，2），所以将点A（4，0）也向右平移2个单位再向上平移2个单位便可得到点D1（6，2）.②AB为对角线时，由于将点C（0，2）向右平移4个单位再向下平移2个单位可得到点A（4，0），所以让点B（-2，0）经过同样的平移步骤便可得到点D2（2，-2）.③BC为对角线时，由于将点A（4，0）向左平移4个单位再向上平移2个单位可得到点C（0，2），所以让点B（-2，0）经过同样平移便可得到点D3（-6，2）.

我们看到，用坐标平移法远比构造方程组求交点方便.通过两道例题的示范，相信同学们已经初步掌握了构造平行四边形的策略：若已知两个定点，可先连接这两点，再将得到的线段按平行四边形的边或对角线分两种情况进行解答；若已知三个定点，可先以三个定点为顶点构造一个三角形，再分别过每个定点作其对边的平行线，三条直线两两相交而成的三个交点都可以是平行四边形的第四个顶点.

江苏省扬州市田家炳实验中学）