具有渐近二次项的一阶离散型哈密尔顿系统同宿轨的存在性
2017-06-05陈文雄
陈文雄
(华侨大学 数学科学学院, 福建 泉州 362021)

具有渐近二次项的一阶离散型哈密尔顿系统同宿轨的存在性
陈文雄
(华侨大学 数学科学学院, 福建 泉州 362021)
讨论具有渐近二次项的一阶离散型哈密尔顿系统同宿轨的存在性.在适当的条件下,利用强不定泛函的临界点定理得到渐近二次的哈密尔顿系统至少有一个非平凡的同宿轨.
哈密尔顿系统; 离散型; 同宿轨; 渐近二次; 临界点理论
1 预备知识
许多学者通过各种方法研究连续哈密尔顿系统的各种解的存在性及多重性[1-13],离散型哈密尔顿系统的研究也得到一些成果[14-24].目前,对于离散型系统解的存在性大多数都集中于周期解,而同宿轨的结果并不多.本文研究的一阶离散型哈密尔顿系统为

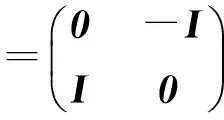

JH(t,x(t)).
(2)
2 基本假设与主要结果

关于非线性项作以下5点假设:
R0) 存在正整数T,使得S(n+T)=S(n),并且对所有n∈Z,J0S(n)是正定矩阵;
R1)R(n,·)∈C1(R2N,R),对于n∈Z,z∈R2N均有R(n+T,z)=R(n,z);
R2)R(n,z)≥0,当|z|→0时,有R(n,z)=o(|z|);
R3) 当|z|→∞时,R(n,z)-S∞(n)z=o(|z|),其中,S∞(n)是实对称矩阵,且λ∞∶=λS∞>2+Λ0;

文中得出如下主要结果.
定理1 设条件R0)~R4)均成立,则系统(1)至少存在一个非平凡的同宿轨.
3 变分框架


(3)
若定义空间E上两个算子A及S,即Ax={-JΔLx(n-1)}n∈Z,Sx={-S(n)x(n)}n∈Z,x∈E,则A及S均是有界线性的自伴算子[14].

(4)
由条件R1)~R3)可知,对任意的ε>0,p≥2,存在Cε>0,使得
|R(n,z)|≤ε|z|+Cε|z|p-1, |R(n,z)|≤ε|z|2+Cε|
且由空间E可连续嵌入到空间lp(Z,R2N)(2 若x∈E是泛函Φ的一个临界点,则由式(6)可知,x是系统(1)的一个同宿轨.因此,要证明文中结果成立,只需证明泛函Φ有非平凡的临界点即可. 为了建立合适的变分框架,需要对自伴算子A+S的谱结构进行分析.以σ(A+S)和σe(A+S)分别表示算子A+S的谱和本质谱,则关于A+S的谱有以下的结论. 命题 1 设R0)成立,则λ0>0,σ(A+S)=σe(A+S),且σ(A+S)⊂[-2-Λ0-λ0]∪[λ0,2+Λ0]. 证明 由R0)及λ0的定义可知,λ0>0.然后,由文献[14]可得σ(A+S)=σe(A+S),且σ(A+S)⊂R/(-λ0,λ0).为了证明最后一个结论,只需证‖A+S‖≤2+Λ0.首先,有 (8) 根据算子A+S的谱结构,空间E具有正交直和分解,即E=E-⊕E+,x=x-+x+.其中:E-,E+均是E的无限维子空间,且在E-,E+上分别有 用|A+S|和|A+S|1/2分别表示算子A+S的绝对值和算术平方根算子,并赋予空间E新的内积(x,y)=(|A+S|1/2x,|A+S|1/2y)l2,则空间(E,(·,·))是希尔伯特空间,且可诱导范数‖x‖=(x,x)1/2.由命题1可得λ0|x|l2≤‖x‖≤(2+Λ0)|x|l2.于是,(E,‖·‖)和(E,|·|l2) 是等价的巴拿赫空间,并且不难得到正交分解E=E-⊕E+,x=x-+x+.对于(·,·)和(·,·)l2均成立.如此可将泛函Φ改写成 (10) 从上述的讨论可知,Φ是强不定泛函. 以下总假设U是可分的自反空间.给定可数子集Σ⊂U*,对每个s∈Σ可定义半范数,有ps∶w→R,ps(w)=|s(u)|+‖v‖,w=u+v∈U⊕V.从而这一族半范数可诱导拓扑TΣ.由参考文献[25],有以下的定理(文献[25]定理4.4的特例). 定理2 设Φ∈C1(W,R)满足以下4个条件: Φ0) 对任意c∈R,Φc是拓扑TΣ中的闭集,Φ′∶(Φc,TΣ)→(W*,ω*)是连续的,其中,ω*表示弱*拓扑; Φ1) 对任意c>0存在ζ>0使得当w∈Φc时,有‖w‖≤‖PVw‖; Φ2) 存在ρ>0使得κ=infΦ(SρV)>0,其中,SρV={v∈V∶‖v‖=ρ}; Φ3) 存在R>0和e∈V∶‖e‖=1使得supΦ(∂Q)≤κ,Q={w=u+te∶t≥0,u∈U,‖w‖≤R},则泛函Φ存在Cc序列{wk},且c∈[κ,supΦ(Q)]. 为了应用定理2讨论函Φ的环绕结构,即Φ满足Φ2)及Φ3).由不等式(4)不难得到下面的引理. 引理2 若条件R0)~R3)成立,则对于任意e∈E+,只要‖e‖=1,则存在R>0,使得当e∈E-⊕Re∶‖x‖≥R时,有Φ(x)≤κ. (11) 由此可得t≠0,若不然,由式(11)有 (12) |t|2-‖y-‖ 再由式(11),(14)可得 这是一个矛盾,所以引理的结论是成立的. 由引理1,2可知,泛函Φ具有环绕结构,即下面的引理成立. 引理3 若条件R0)~R3)成立,设e∈E+,且‖e‖=1,则存在R0>0,使supΦ(∂Q)≤κ,Q={x=x-+te∶t≥0,x-∈E-,|x|≤R0}. 而对于泛函Φ的Cc序列,有以下性质成立. 引理4 若条件R0)~R4)成立,则Φ的任意Cc序列均有界. 证明 设有序列{xk}⊂E满足 Φ(xk)→c, (1+‖ 则存在C0>0,使得 (n)). (18) 假设序列{xk}无界,则在子列的意义下有‖xk‖→∞.令yk=xk/‖xk‖,则‖yk‖=1.又由于有 所以,结合式(17)可得 下面分两种情形进行讨论. 故而有 类似引理2的讨论可证明 |||w(n)| 这是不可能的,事实上,对任意的x∈E,有 |(A+S)x-S∞x|l2≥|S∞x|l2-|(A+S)x|l2≥(λ∞-2-Λ0)|x|l2. 而由条件R3)可知,λ∞-2-Λ0>0,这意味着0∉σ(A+S-S∞). (29) 这与式(18)矛盾. 综上所述,引理4的结论成立. 对于定理1的证明可应用定理2.取U=E-和V=E+,则U=E-是可分的自反空间,从而可取U*的可数子集Σ⊂U*. 定理1的证明,泛涵Φ满足Φ0)和Φ1)(证明是一个相对标准的过程,在此不再累述,可参见文献[13]).引理3说明泛函Φ具有环绕结构,即满足Φ2)和Φ3).由定理2可知,泛涵Φ存在Cc序列{xk}⊂E,且其水平c≥κ>0,又由引理4可知,序列{xk}是有界的. 不妨设‖xk‖≤M(M>0),则等式 (30) 成立.因此,可得存在τ>0及nk∈Z,使得|xk(nk)|≥τ.若不然由引理3的证明,可得|xk|lp→0(p>2). (31) 这与ε [1] BARTSCH T,DING Yanheng.Homoclinic solutions of an infinite-dimensional Hamiltonian system[J].Math Z,2002,240(2):289-310. [2] ARIOLI G,SZULKIN A.Homoclinic solutions of Hamiltonian system with symmetry[J].Journal of Differential Equations,1999,158(158):291-313. [3] ZELSTI V C,EKELAND,SÉRÉ E.A variational approach to homolinic orbits in Hamiltonian systems[J].Math Ann,1990,288(1):133-160. [4] DING Yanheng,GIRARDI M.Infinitely many homoclinic orbits of a Hamiltonian system with symmetry[J].Nonlinear Anal,1999,38(3):391-415. [5] DING Yanheng,WILLEM M.Homoclinic orbits of a Hamiltonian system[J]. Z Angew Math Phys, 1999, 50(5):759-778. [6] HOFER H,WYSOCKI K.First order elliptic systems and the existence of homoclinic orbits in Hamiltonian systems[J].Math Ann,1990,288(1):483-503. [7] SÉRÉ E.Existence of infinitely many homoclinic orbits in Hamiltonian systems[J].Math Z,1992,209(1):27-42. [8] SZULKIN A,ZOU Wenming.Homoclinic orbits for asymptotically linear Hamiltonian systems[J].J Funct Anal,2001,187(1):25-41. [9] TANAKA K.Homoclinic orbits in a first order superquadratic Hamiltonian system: Convergence of subharmonic orbits[J].J Differ Equations,1991,94(2):315-339. [10] DING Y H.Multiple homoclinic in a Hamiltonian system with asymptotically or super linear terms[J].Comm Cont Math,2006,8(4):453-480. [11] DING Yanheng,JEANJEAN L.Homoclinic orbits for a nonperiodic Hamiltonian system[J].J Differ Equations,2007,237(2):473-490. [12] DING Yanheng,LEE C.Existence and exponential decay of homoclinics in a nonperiodic superquadratic Hamiltonian system[J].J Differ Equations,2009,246(7):2829-2848. [13] 梁小花,张金顺.一个N维Hamilton系统的Painleve′分析与精确解[J].华侨大学学报(自然科学版),2007,28(3):327-329. [14] CHEN Wenxiong,YANG Minbo,DING Yanheng.Homoclinic orbits of first order discrete Hamiltonian systems with super linear terms[J].Science China Mathematics,2011,54(12):2583-2596. [15] YU Jianshe,BIN Honghua,GUO Zhiming.Multiple periodic solutions for discrete Hamiltonian systems[J].Nonlinear Anal,2007,66(7):1498-1512. [16] GUO Zhiming,YU Jianshe.Periodic and subharmonic solutions for superquadratic discrete Hamiltonian systems[J].Nonlinear Anal,2003,55(7/8):969-983. [17] ZHENG Bo.Multiple periodic solutions to nonlinear discrete Hamiltonian systems[J].Advancesin Difference Equations,2008,2007(1):1-13. [18] DENG Xiaoqing.Periodic solutions for subquadratic discrete Hamiltonian systems[J].Advancesin Difference Equations,2008,2007(1):1-16. [19] DENG Xiaoqing,CHENG Gong.Homoclinic orbits for second order discrete Hamiltonian systems with potential changing sign[J].Acta Appl Math,2008,103(3):301-314. [20] AHLBRANDT C D.Equivalence of discrete Euler equations and discrete Hamiltonian systems[J].J Math Anal Appl,1993,180(2):498-517. [21] BOHNER M.Linear Hamiltonian difference systems: Disconjugacy and Jacobi-type conditions[J].J Math Anal Appl,1996,199(3):804-826. [22] CHEN S.Disconjugacy, disfocality, and oscillation of second order difference equations[J].J Differ Equations,1994,107(107):383-394. [23] ERBE L H,YAN Pengxiang.Disconjugacy for linear Hamiltonian difference systems[J].J Math Anal Appl,1992,167(2):355-367. [24] HARTMAN P.Difference equations: Disconjugacy, principal solutions, Green′s functions, complete monotonicity[J].Trans Amer Math Soc,1978,246(12):1-30. [25] BARTSCH T,DING Yanheng.Deformation theorems on non-metrizable vector spaces and applications to critical point theory[J].Math Nachr,2006,279(12):1267-1288. (责任编辑: 陈志贤 英文审校: 黄心中) Existence of Homoclinic Orbit in First Order Discrete Hamiltonian System With Asymptotically Quadratic Term CHEN Wenxiong (School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China) This paper discusses the existence of homoclinic orbit in first order discrete Hamiltonian system with asymptotically quadratic term. Under certain assumptions, we obtain that the asymptotical Hamiltonian system has at least one non-trivial homoclinic orbit via critical point theory for strongly indefinite functional. Keywords:Hamiltonian system; discrete type; homoclinic orbit; asymptotically quadratic; critical point theory 10.11830/ISSN.1000-5013.201703025 2016-09-18 陈文雄(1981-),男,讲师,博士,主要从事线性分析的研究.E-mail:cwx2636@hqu.edu.cn. 国家自然科学基金资助项目(11226115) O 175.7 A 1000-5013(2017)03-0424-06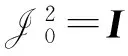

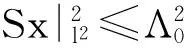



4 环绕结构和Cc序列
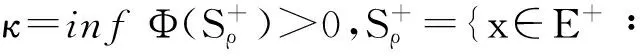














5 主要结论的证明